粒子群算法自寻优模糊PID控制器设计
杨洋,张秋菊
(1. 江南大学 机械工程学院,江苏 无锡 214122; 2. 江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122)
0 引言
近年来,随着“工业4.0”的提出,工业伺服控制领域向着智能化方向发展。部分厂家已经将参数自寻优自适应功能作为开发新一代伺服控制器的必备功能[1]。目前,市场上的伺服控制器通常采用PID控制方法,PID控制器的参数整定问题又是伺服控制的难点问题[2-4]。不少学者将智能控制与传统的PID控制方法相结合来实现控制系统的智能化,使之具有自寻优、自适应的能力。
目前,智能控制策略主要是基于模糊控制理论、神经网络控制以及遗传算法理论等[5-7]。模糊控制理论诞生以来应用于许多领域,取得了良好的控制效果[8]。自从1974年第一台模糊控制器[9]诞生以来,人们对模糊控制器投入了极大的研究热情,并已经得到了广泛的研究和应用[10]。然而模糊PID控制也有其缺点,它过分地依赖于专家经验而无法满足特殊条件下的抗干扰能力。一旦模糊控制器确定,控制规则和控制器参数也就随之确定,降低了控制系统的自适应能力。所以对模糊PID控制器还需要对其参数进行优化。群智能算法的发展为模糊PID参数控制器的优化提供了一种高效的方法。
群智能优化方法是借鉴仿生学的特点发展起来的一门新兴的优化计算方法,最早由Beni、Hackwood和Wang在分子自动机系统中提出[11-12]。粒子群算法(particle swarm optimization, PSO)是模拟鸟类捕食行为的群体智能算法,由美国电气工程师Eberhart和社会心理学家Kennedy于1995年提出[13]。由于PSO算法容易实现,需要调整的参数少,一经提出就受到了研究者的重视,被广泛应用到各个领域当中[14]。
本文基于粒子群算法优化模糊PID控制器,通过对控制器的量化因子Ke、Kec、比例因子Ku进行寻优,使得系统的权系数可调,解决模糊控制器过于依赖专家经验的缺点,进而实现PID参数的智能调节。通过Matlab仿真结果对比,可以看出参数自寻优控制器与经典PID控制器和模糊PID控制器相比,具有更优越的动态响应性能,大幅提升了设备的整体运行性能。
1 永磁同步电机伺服系统数学模型
1.1 永磁同步电机的数学模型
三相永磁同步伺服电机的模型是一个多变量、非线性、强耦合系统。通过坐标变换可以将三相坐标系统变换到dq两相坐标系中,使得数学模型简化[15]。得到永磁同步电机模型如下:
(1)
(2)
3)电磁转矩方程:Te=Pn(Ψdiq-Ψqid)
(3)
(4)
1.2 工程整定法PID参数确定
课题先采用试凑法得到PID参数的最佳初始值。先将积分时间设置为无穷大,微分时间设置为0,比例环系数KP按照经验设置初始值,运行控制系统,逐渐增大比例环系数KP,得到满意的控制曲线。将比例系统KP设置为纯比例控制时的5/6,然后再引入积分环节,将积分系数从大到小进行整定,直到获得满意的控制效果。具体实验过程如下:
1)KP参数确定
进行比例系数KP的调节时,先将Ki参数设定为无穷大,实际操作中将Ki取100 000代表无穷大。测得电机的转动情况如表1所列。

表1 P控制器参数调节实验
可以看出在KP=8时候,电机有明显的振动情况出现,初步选定KP=8。
2) PI控制器KP取值
PI控制器中KP为纯比例控制的5/6,
KP=8×5/6=6.67
3)Ki参数确定
进行Ki参数调节时,将KP参数设为6.67。Ki参数由大到小实验,测得电机转动情况如表2所列。
初步选定KP=6.67,Ki=0.005,此时电机转动效果最好。
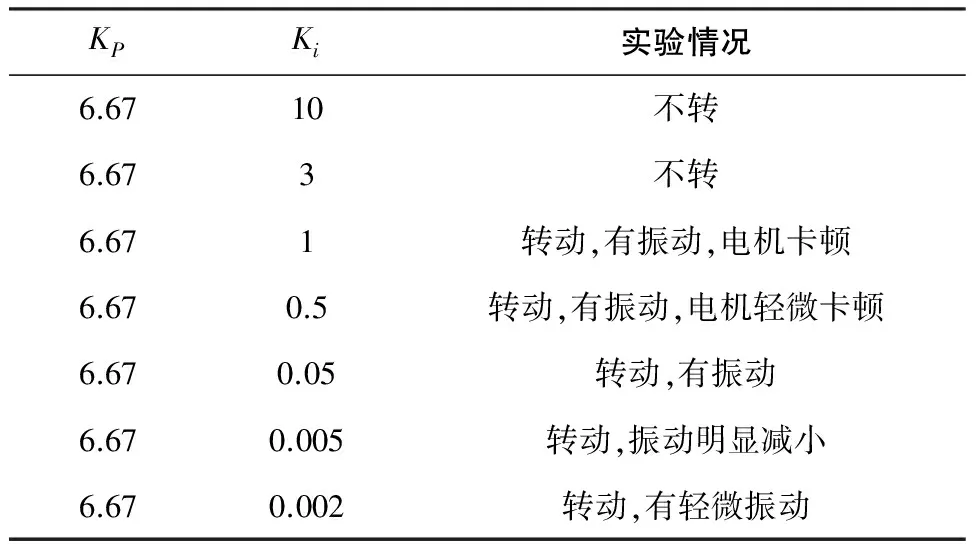
表2 PI控制器参数调节实验
2 参数自寻优模糊PID控制器设计
2.1 Ke、Kec、Ku对系统的影响
模糊PID控制器的量化因子Ke、Kec、比例因子Ku都会对控制器的响应输出产生影响,Ke越大,系统响应越快。Ke过大时,系统会产生超调,振荡的现象,Ke过小,则系统的收敛速度放慢。Kec越大,系统表现的越为迟钝,Kec越小,系统则越为灵敏,但严重时候会产生振荡。Ku为输出的比例因子,对整个系统的响应输出影响最大,Ku越大,响应速度越快,Ku过大,则会出现振荡现象,Ku过小,则收敛速度太慢。通过对Ke、Kec、Ku参数的寻优,可以很好地解决模糊控制器控制参数不变所带来的问题,提高了系统的自适应能力。
2.2 粒子群算法优化参数设计
粒子群算法是模拟鸟类发觅食行为的算法。每个需要被优化的问题都是搜索空间的一只鸟,称之为“粒子”。所有的粒子都有一个被优化函数所决定的适应值,每个粒子还有一个速度来决定它们的飞行方向和距离,粒子追随当前的最优粒子在解空间中搜索。
标准粒子群算法公式:
vk+1=ωvk+c1(pbestk-xk)+c2(gbestk-xk)
(5)
xk+1=xk+vk+1
(6)
式中,ω称为惯性权重或者惯性因子,改变粒子的大小能够决定粒子当前速度继承的大小;vk是粒子的速度向量;xk是当前粒子的位置;pbestk表示粒子本身找到的最优解的位置;gbestk表示整个种群目前找到的最优解的位置;c1和c2称为学习因子,通过改变c1和c2值的大小可以调整pbestk和gbestk对粒子吸引的影响强度。
本文通过粒子群算法对模糊控制器的量化因子Ke、Kec、比例因子Ku进行寻优,以积分性能指标(ITAE)作为寻优的目标,根据控制系统实际响应中不同阶段的误差和误差变化率进行寻优。
2.3 确定适应度函数
ITAE指标是一种具有较好的实用性和选择性的指标,它能够综合评价控制系统的动态和静态性能,在工程问题中得到了广泛的应用。采用ITAE指标可以保证系统的快速响应性,超调量,调节时间以及稳态误差等。ITAE是时间乘以误差绝对值积分的性能指标,即:

(7)
2.4 粒子群算法寻优基本流程
1) 确定控制器参数Ke、Kec、Ku的取值范围,初始化系统的种群,包括种群的初始位置和种群的初始速度,迭代次数,学习因子,惯性因子;
2) 根据式(7)评估每个粒子的适应度;
3) 对每个粒子,将其适应值与其经过的最好位置pbestk作比较,如果较好,则将其作为当前的最好位置;
4) 对每个粒子,将其适应值与其全局经过的最好位置gbestk作比较,如果较好,则将其作为全局的最好位置;
5) 根据式(5)和式(6)更新粒子的速度和位置;
6) 如果达到结束条件(通常为足够好的适应值或者达到迭代的次数)则继续执行下一步,否则跳转回2);
7) 得到种群的最好位置gbestk来确定量化因子Ke、Kec、比例因子Ku,然后进行模糊PID控制,得到系统的输出响应,返回2)继续执行。
粒子群算法的流程图如图1所示。

图1 粒子群算法流程图
3 基于粒子群优化算法模糊PID控制器设计
3.1 参数自寻优模糊PID系统控制原理
基于粒子群算法寻优模糊PID控制器采用二维模糊控制器结构,转速输入的误差e和误差变化率ec作为控制器的输入量,经过量化因子Ke、Kec的调整,转化为模糊控制器的输入E,EC。U为模糊控制器的输出,经比例因子Ku转化为实际的输出。Ke、Kec、Ku采用粒子群优化算法实现自寻优功能。系统的结构框图如图2所示。

图2 参数自寻优模糊PID控制结构框图
3.2 模糊PID控制器设计
要实现模糊PID控制,首先要找出PID参数与误差e和误差变化率ec之间的模糊关系,在系统运行过程中不断进行模糊推理和模糊预算,对PID参数进行在线整定,从而使得被控对象具有良好的动态响应性能[16]。
1) 控制器的输入变量有两个:速度误差e以及误差变化率ec,经过量化因子Ke、Kec的调整,转化为模糊控制器的输入E、EC;
2) 控制器的输出为PID参数的修正量ΔKP、ΔKi、ΔKd,经比例因子Ku转化为实际的输出;
3) 定义各语言变量的语言值和隶属度函数。
为了便于工程实现,通常把输入变量范围人为地定义成离散的若干级,所定义级数的多少取决于所需输入量的分辨率。
输入变量有两个,E以及EC,论域为{E,EC}={-3,-2,-1,0,1,2,3},对应的语言为:{NB,NM,NS,Z,PS,PN,PB}输出变量有ΔKP、ΔKi、ΔKd,其中其ΔKP的论域为{-0.3,-0.2,-0.1,0,0.1,0.2,0.3}。ΔKi的论域为{-0.06,-0.04,-0.02,0,0.02,0.04,0.06}。ΔKd的论域为{-3,-2,-1,0,1,2,3}。对应的语言均为{NB,NM,NS,Z,PS,PM,PB}。
隶属度函数选择三角形对称分布的隶属度函数,实践证明其性能满足使用需求。
4) 建立模糊控制规则表如表3所列。

表3 ΔKP、ΔKi、ΔKd模糊控制规则表
4 控制系统建模仿真
4.1 基于粒子群算法寻优模糊PID控制器系统建模
1) 在simulink下进行系统的仿真实验。matlab中提供S-function来自己定制模块。将粒子群算法写成M文件导入S-function中,并将其封装为一个两输入,三输出的子系统。如图3所示。

图3 粒子群算法S-function
2) 电机通常可以简化为典型的二阶系统,选取式(8)做为被控对象,在matlab下进行初步的仿真验证。
(8)
3) 基于粒子群寻优算法模糊PID控制系统的仿真模型如图4所示。主要分为粒子群算法部分,模糊控制器部分,PID控制部分。
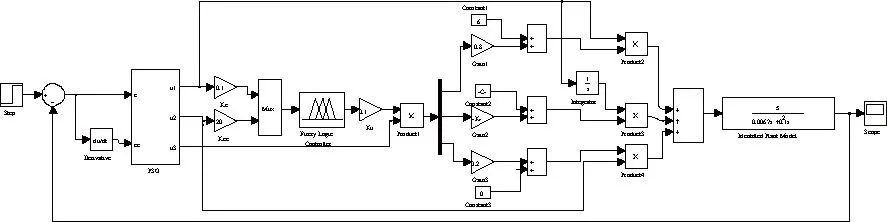
图4 基于粒子群寻优算法模糊PID控制系统仿真图
4.2 仿真结果与比较
利用Matlab的simulink模块进行仿真,设定直驱转塔刀架电机的目标转速为3 000 r/min,分别进行经典PID、模糊PID和粒子群算法寻优模糊PID控制系统仿真,仿真结果如图5所示。分析图中的仿真曲线可以看出,粒子群算法寻优的模糊PID控制器是三者中控制效果最为理想,在超调量、动态响应速度以及稳态误差方面得到了显著的改善效果。

图5 PID、模糊PID、粒子群算法寻优模糊PID仿真曲线图
5 结语
对交流永磁同步电机建模分析并且分别设计了经典PID控制器,模糊PID控制器以及基于粒子群算法寻优的模糊PID控制器。通过仿真实验可以看出基于粒子群算法寻优的模糊PID控制器既有着模糊控制器的优良控制效果又解决了由于模糊PID控制器的控制规则和控制参数固定不变所带来的问题。通过仿真对比试验可以看出基于粒子群算法寻优的模糊PID控制器有着更优越的控制效果。
[1] 李鹏. 2014年伺服行业状况略谈[J]. 伺服控制,2015(Z1):9-12.
[2] 邱丽,曾贵娥,朱学峰,等. 几种PID控制器参数整定方法的比较研究[J]. 自动化技术与应用,2005,24(11):31-34.
[3] 杨智,朱海锋,黄以华. PID控制器设计与参数整定方法综述[J]. 化工自动化及仪表,2005,32(5):1-7.
[4] 段力学. PID参数整定方法分类与概述[J]. 现代计算机(专业版),2012(5):23-26.
[5] 刘莉宏. 基于智能控制的PID控制方式的研究[J]. 北京工业职业技术学院学报,2012,11(2):33-38.
[6] 王威,杨平. 智能PID控制方法的研究现状及应用展望[J]. 自动化仪表,2008,29(10):1-3+7.
[7] 闫永跃,李庆周,于树新. 智能PID控制综述[J]. 可编程控制器与工厂自动化,2006(12):9-13,106.
[8] 秦绪平,谭国俊. 模糊控制理论的发展应用与展望[J]. 控制工程,2005,12(A2):141-143.
[9] Mamdani E H. Application of Fuzzy Logic to Approximate Reasoning Using Linguistic Synthesis[J]. IEEE Transactions on Computers,1977,26(12):1182-1191.
[10] Berenji H.R, Khedkar P.S. Using fuzzy logic for performance evaluation in reinforcement learning[J]. International Journal of Approximate Reasoning,1998,18(1):131-144.
[11] Hackwood S, Wang J. The Engineering of Cellular Robotic Systems[C]. IEEE International Symposium on Intelligent Controll,1988: 70-75.
[12] Hackwood S,Beni G.Self-organization of Sensors for Swarm Intelligence[C]. IEEE International conference on Robotics and Automation, 1992:819-829.
[13] Kennedy J , Eberhart R.C. Particle Swarm Optimization[J]. IEEE Inter. Conf. on Neural Networks, 1995:1942-1948.
[14] 李宁,付国江,库少平,等. 粒子群优化算法的发展与展望[J]. 武汉理工大学学报(信息与管理工程版),2005,27(2):26-29.
[15] 袁登科,徐延东,李秀涛. 永磁同步电机变频调速系统及其控制[M]. 北京:机械工业出版社,2015:33-36.
[16] 孙华,戴跃洪. 永磁同步直线电机的模糊参数自寻优控制及仿真[J]. 机械设计与制造,2011(12):107-108.

