标签零模型及子图分布算法应用研究
邹晓红,郭景峰,2,贺释千,2,陈 晶,刘院英
1(燕山大学 信息科学与工程学院,河北 秦皇岛 066004)2(河北省虚拟技术与系统集成重点实验室,河北 秦皇岛 066004)3(河北经贸大学 信息技术学院,石家庄 050061)
1 引 言
图是表现力很强的数据结构,能够充分表示实体自身的信息及实体间的联系,因而在生物信息学、化学等领域广泛应用.并且随着对结构化数据分析需求的大量增加,通过图建模进行图挖掘问题已经成为一个非常重要的研究课题.图分类是图挖掘的一个重要研究分支[1],而图向量化是图分类的基础,通过对图提取特征向量化后根据得到的图向量可以进行图分类.目前关于图分类的研究中能用于提取分类特征的算法有两类,一类是子图分布算法,另一类是频繁子图挖掘算法.用于图分类的子图分布算法的相关研究最早起源于生物学与社会网络等领域,其目的是检测图的非平凡特性用于发现不同图之间的异同,在生物学研究中,通过检测两组蛋白质交互网络的拓扑结构的不同可以发现两者功能上的差异.例如通过把要检测物质的化学结构和已知的致癌症物质抽象成图比对,就可以初步判断要检测物质是否致癌.
国外对用于图分类的子图分布算法研究已经有很多,一般是基于一定的图模型,将现实世界中的网络抽象为图并建模,在构建图模型的基础上再进行算法研究.如文献[2]中首先定义小诱导子图为Graphlet,简称为Graphlet模型,提出使用Graphlet频度来测量网络局部的拓扑结构,给出了相对图频率距离公式和算法.2008年Przulj N与Milenkovic′T对GDD改进,在文献[3]中提出了GDV,又称为图签名和图签名相似度以及图签名距离.GDV是一个图向量,存放子图分布信息,并根据图的不同维度给出了相应的权值,用于调节因为网络的拓扑结构导致某些维度的数据严重偏高或严重偏低.2015年Ahmed N等人在文献[4]中提出了PGD算法,拓展Graphlet的定义,根据改进后的Graphlet模型计算子图分布,利用补图对所有子图进行了组合,利用组合数学公式减少了部分子图的计算.2015年Elenberg E R等人在文献[5]中提出了3-Profiles,描述有3个顶点的图,可用于计算聚类系数,在社会网络里,聚类系数反映了人们间联系的紧密程度.该算法利用马尔科夫链建模并估算3-Profiles分布.国内的子图分布研究相对较少,谭尚旺等人对随机完全图中某些子图的概率分布进行了研究并给出极限定理[6].
随着图分类在诸多领域的广泛应用,如何提高分类的准确性变得尤为重要.但是,根据Graphlet模型及改进的模型计算的子图分布只考虑到图的拓扑结构信息,并未考虑图中顶点和边标签信息,用于图分类时,因为提取的图分类特征过少而影响图分类的准确性.对此本文加以改进,首先,借鉴统计学的零模型构建了n阶标签零模型,该模型同时考虑图的拓扑结构信息和图中顶点和边标签信息,增加图分类的特征,提高图分类的准确性.其次,针对直接计算子图分布,需要反复多次进行图同构测试,导致时间复杂度较高的问题,在n阶标签零模型基础上提出两个算法,一个是用于构建图索引的BGLI算法,另一个是在BGLI算法基础上提出的计算子图分布ESGS算法,降低时间复杂度,提高计算速度.
2 标签零模型
定义1.标签图:设G=(V,E,Σ,L),其中V(G)和E(G)分别为图G的顶点集和边集、Σ为标签集,L为标签的映射函数:对于∀v∈V(G)记为L(v),对于∀(vi,vj)∈E(G)记为L(vi,vj),用于映射顶点和边的标签.
定义2.图同构:图同构是双射函数f使得f:V(G)→V(H),若标签图G和标签图H同构,则满足下列条件:
1)若∀v∈V(G),∀v′∈V(H)
则v↔v′,记为V(G)↔V(H).
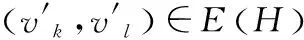
则(vi,vj)↔(vk′,vl′),记为E(G)↔E(H).
3)若∀v∈V(G),∀v′∈V(H)
则L(u)=L(v)
4)若∀(vi,vj)∈E(G),∀(vk′,vl′)∈E(H)
则L(vi,vj)=L(vk′,vl′)
图同构表明,若标签图G和标签图H同构,则V(G)与V(H)一一对应且对应顶点的标签相同,E(G)与E(H)一一对应且对应边的标签相同.
定义3.n阶零模型:n阶零模型是与原图G具有相同统计量的随机图H.设统计量有原图G的顶点数N、边数M和n个顶点的联合度分布p(d1,d2,…,dn)(n≤N),其中dn为顶点度为n的个数.要求根据原图G生成的图H满足如下约束:
1)|V(G)|=|V(H)|=N
2)|E(G)|=|E(H)|=M
3)pG(d1,d2,…,dn)=pH(d1,d2,…,dn)(n≤N)
n阶零模型是n阶零配置模型的简称,n阶零模型中的n个顶点的联合度分布表明的是,具有n个顶点的子图形成的子图分布,并且当n>1时,要求这n个顶点所形成的子图为连通图,不出现孤立顶点.下面举例说明各阶模型:
0阶零模型:与原图G具有相同顶点数N、边数M和顶点的平均度D的随机图,其中平均度D是G中所有顶点的度的平均值D=2M/N.
1.阶零模型:与原图G具有相同顶点数N、边数M、平均度D和度分布为p(d)的随机图,其中度分布p(d)是指原图G中顶点度频率分布[7].
2.阶零模型:与原图G具有相同的两个顶点联合度分布p(di,dj)和1阶零模型中的所有约束条件的随机图.其中di是度为i的顶点,dj是度为j的顶点,p(di,dj)为两个顶点联合度分布,是指每条边两端连接顶点度的联合度分布.
3.阶零模型:与原图G具有相同的三个顶点联合度分布p(di,dj,dk)和2阶零模型中的所有约束条件的随机图.三个顶点联合度分布考虑到三个顶点之间的相互连接性,主要有两种情况,一种是开三角形,另一种是闭三角形,即保证与原图G具有相同的开三角形和闭三角形分布.
n阶零模型如图1所示,其中左边的(a)图为原图,(b)到(e)图分别为根据原图提取的0到3阶模型生成的随机图[8].文献[8]用实验验证了根据原图G提取统计量达到3阶零模型时,生成的新图H已经比较好的还原了原图.当阶数n等于原图G的顶点数N时,n阶零模型的约束最强.
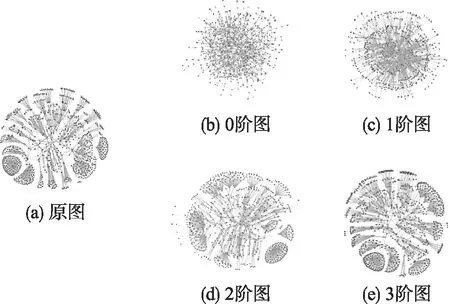
图1 零模型示例Fig.1 Null model example
本文根据n阶零模型提出了n阶标签零模型用于计算子图分布,同时考虑图中顶点和边标签信息.n阶标签零模型的定义如下:
定义4.n阶标签零模型:n阶标签零模型是与原图G具有相同统计量的随机图.设统计量有原图G的顶点数N、边数M和n个顶点的联合标签分布p(L(v1),L(v2)…L(vn)),(n≤N)其中v1,v2…vn∈V(G),L(vn)为vn的标签,以及这n个顶点间边上标签形成的联合标签分布p(L(e1),L(e2)…
L(em))(m≤M),其中e1e2…em∈E(G),L(em)为em的标签.
要求根据原图G生成的图H满足如下约束:
1)|V(G)|=|V(H)|=N
2)|E(G)|=|E(H)|=M
3)pG(L(v1),…,L(vn))=pH(L(v1),…,L(vn))
4)pG(L(e1),…,L(em))=pH(L(e1),…,L(em))
其中(n≤N),(m≤M)
下面举例说明各阶模型,如图2所示,图中所示为根据标签零模型对标签图计算所形成的联合标签分布,即n阶标签零模型对应的子图分布.为方便举例,图中边标签已省略.
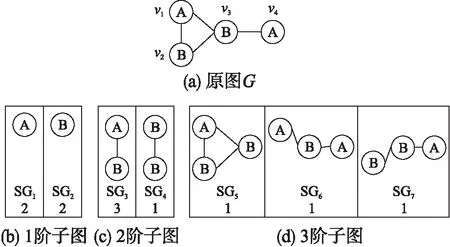
图2 标签零模型子图分布示例Fig.2 Subgraph distribution of label null model example
1.阶标签零模型:与原图G具有相同顶点数N、边数M、顶点标签分布p(L(vi))的随机图.即要求与原图G具有相同的顶点数N、边数M、顶点标签数、顶点标签种类数、每种顶点标签中的标签数、边标签数、边标签种类数、每种边标签中的标签数.
2.阶标签零模型:与原图G具有相同的两个顶点联合标签分布p(L(vi),L(vj))、这两个顶点间的边标签分布p(L(ei′))和1阶标签零模型中的所有约束条件的随机图.其中顶点vi的标签为L(vi),顶点vj的标签为L(vi),p(L(vi),L(vj))为两个顶点的联合标签分布,是指每条边两端连接顶点的联合标签分布,p(L(ei′)是这两个顶点间边的标签分布.
3.阶标签零模型:与原图G具有相同的三个顶点联合标签分布p(L(vi),L(vj),L(vk)),这三个顶点间的三条边联合标签分布p(L(ei′),L(ej′),L(ek′))和2阶标签零模型中的所有约束条件的随机图.
根据n阶标签零模型提取图G中n个顶点的子图,该子图包括了n个顶点及其互相连接的边,其中包括顶点和边的标签,即根据顶点提取的诱导子图.因为各阶子图的种类和每种子图的个数由n阶标签零模型唯一确定,所以子图分布为同一分布是图同构的必要条件.下面给出定理和证明.
定理1.若图G与图H同构,且要求图G与图H的顶点集、边集和标签集都为有限集或可列集,则根据n阶标签零模型计算的子图分布必为同一分布,即两图的子图分布为同一分布是两图同构的必要条件.
证明:当n阶标签零模型的阶数等于1时.因为图G与图H同构,所以图G与图H拥有相同标签的顶点一一对应,并且标签的种类数相同,每种子图拥有相同标签的顶点的个数也相同.因此,当阶数等于1时,子图分布退化成标签分布,此时定理显然成立.
当n阶标签零模型的阶数n等于大于1时,用反证法证明,假设图G与图H同构,对应的子图分布分别为FG和FH,且为不同分布.
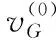
(1)
(2)
(3)
……,……
(4)
因为MG=MH所以
(5)
(6)
因此可知在图G与图H中分别选取n个顶点的分布分别一一对应,这些分布联合后分别为FG和FH,图G与图H的分布FG和FH是同一分布,与假设矛盾.所以两图的子图分布为同一分布是两图同构的必要条件,该必要条件证明了n阶标签零模型用于图分类的有效性.
问题1.子图分布估计问题:设图G有N个顶点,M条边,L个标签,SGi是G中的子图.若SGi在图G中有Ci个与其同构的子图,记其频度为Ci,在G中根据标签零模型选取具有n个顶点的子图SGi,将子图集合{SGi}作为基本事件集,要求据此估计子图分布.
为描述子图分布需要引入随机变量X,设X为一随机变量
F(x)=P{X=φ(SGi)}=pi
(7)
其中{xi=φ(SGi)|(i=1,2…)},φ(SGi)∈[1,+).pi满足条件:为随机变量X的分布函数,简称分布.
其中φ是一个标识函数,用于给每一个SGi一个唯一标识,用于图向量化,子图的编号从1开始到+.根据标签零模型计算子图分布,然后把提取的子图及其频度以向量的形式作为图分类特征进行图分类.因为大多数分类算法不能直接把子图作为特征计算,所以需要给每一个子图一个唯一标识进行向量化.
为估算子图分布可以通过采样估算子图总体分布,样本分布近似替代总体分布会有一定的偏差,为此需要知道当样本量一定时,样本分布提取了总体分布多少信息,即量化样本信息提取比.
问题2.量化样本信息提取比问题:假设穷举图G中所有子图,可得到G图中所有子图的总体分布,简称总体分布,记为p(x).在图G中采样,当子图样本,简称为样本,量为k时,可得到此k个子图的样本分布,简称样本分布,记为q(x).要求据此定量分析q(x)在p(x)中提取了多少信息.
对于给定的概率分布可用信息熵进行量化,因为子图分布是概率分布,所以使用信息熵量化子图分布信息.
定义5.信息提取比例:
r=Hq/Hp
(8)
信息提取比例是指样本信息占总体信息的比例,简称信息提取比,其中Hp为总体分布的熵值,简称总体熵值,Hq为样本分布熵值,简称样本熵值.
样本熵值可以通过样本直接计算,而对于总体熵值,当总体分布的信息熵收敛的情况下,可以通过穷举计算出总体熵值,但时间复杂度是NP,所以可以根据最大熵原理推断出总体最大熵分布,推断出总体的极限熵值,近似替代总体熵值.考虑到实际需求,在样本中最容易提取也最具有一般意义的统计量是均值和方差,所以假设均值和方差都存在的情况下,根据最大熵原理和相对熵推断出总体最大熵分布.子图分布本身是离散型分布,最大熵原理对离散或连续型分布都适用,为方便计算,令每个子图映射为一个数,且要求这些映射数相互间隔大于1.经映射后,xi表示一个子图.约束条件,xi在[1,+)区间内,总体的参数均值μ、总体的参数方差σ2都存在时,总体最大熵分布p(x)就是正态分布N(μ,σ2).
设:总体最大熵分布的概率密度函数为p(x),简写为p、熵函数为H(p)、总体的参数均值、总体的参数方差σ2、总体的极限熵值Hp.样本的分布概率密度函数为q(x),简写为q、熵函数为H(q)、样本统计量均值x、样本统计量方差s2、样本的信息熵Hq.
由相对熵公式可知
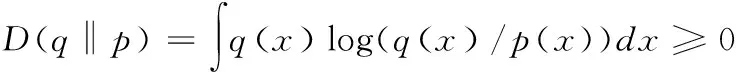
(9)
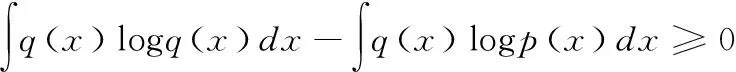
(10)
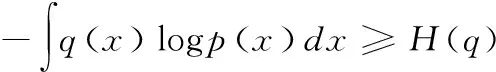
(11)
当均值μ和方差σ2都存在时,取p(x)=N(μ,σ2)则
(12)
令底数为e得
(13)
(14)
由于q(x)的均值方差有如下关系
(15)
所以
(16)
当p(x)=N(μ,σ2)时,上式取等号.根据最大熵原理求出总体最大熵分布后,就可以根据上式计算其极限熵值.
3 子图分布算法
3.1 算法主要思想
子图分布最基本的两个步骤是:第一步,对图进行采样.其中,样本是图中的子图.第二步,对采集的样本进行图同构检测,并对其计数.
计算子图分布过程中,不进行任何优化直接计算,会不可避免反复多次进行图同构测试,导致相对较高时间复杂度.设k为采样的子图数,则k个具有n个顶点的子图需计算k2n!次.所以计算子图分布的时间复杂度是O(k2n!).因为直接搜索子图需多次进行扫描遍历,会耗费很多时间,尤其是在分布式的情况下,多机并发搜索子图会极大增加网络开销减慢算法效率.而建立一个合适的索引实现对子图的快速查找,可以避免多机并发搜索子图,并通过每个索引找到关于子图的信息,减少搜索时间.
为此,本文根据n阶标签零模型提出两个算法,一个是用于构建GLI索引的BGLI(Build Graph Location Index)算法,另一个是在BGLI算法基础上提出的计算子图分布ESGS (Estimate SubGraph on Spark)算法.
3.2 基于图不变量的图索引
图不变量是图自身的属性.如果两个图同构,那么它们不但拥有相同的拓扑结构而且也具有相同的图不变量,反之,该性质不成立,即不变量是判定图同构的必要非充分条件.例如一个图的顶点数和边数就是两个图不变量,图中最大顶点度也是图不变量.对于同构的图其图不变量都是相同的,而图不变量相同的图不一定同构,所以,图不变量不能直接用在同构子图的匹配或计数上.然而,图不变量可以用来对非同构图进行过滤,缩减搜索空间,间接提高算法效率.
本文提出两个函数,图似然函数和顶点度映射函数.这两个函数分别利用标签信息和顶点度建立图不变量.
定义6.图似然函数(Graph Likelihood function):
(17)
该函数是利用子图中顶点和边的标签信息建立的图不变量.其中G为标签图,SG为G的子图,pi是G中顶点标签i的频率,ci是SG中标签i的出现次数,CN为SG中标签总数.其中标签分为顶点标签和边标签两种情况.图似然函数,简称GL函数.
定理2.若SG和SG′同构,则
gl(G,SG)=gl(G,SG′)
(18)
定理可以分别应用于顶点标签和边标签,得到下列等式:
glv(G,SG)=glv(G,SG′)
(19)
gle(G,SG)=gle(G,SG′)
(20)
证明:设标签图G有N个顶点,M条边,SG和SG′是G的子图.epi是G中边标签i的频率,eci和ec′i分别是SG和SG′中边标签i的出现次数,CLE(SG)为SG边标签的种类集合,|CLE(SG)|=em,CLE(SG′)为SG′边标签的种类集合,|CLE(SG′)|=em′,若SG和SG′同构,则当标签为边标签时:
gle(G,SG)=gle(G,SG′)
(21)
(22)
若SG和SG′同构,则SG和SG′共同拥有图G的子边标签集合{L1,L2,…,Li}=CLE(SG)=CLE(SG′)并且边标签集合中的标签满足下列等式
ec1=ec′1,ec2=ec′2,…,eci=ec′i
(23)
两边分别乘以各自边标签Li的频率的对数log(epi)得
ec1log(ep1)=ec′1log(ep1)
(24)
ec2log(ep2)=ec′2log (ep2)
(25)
…
ecilog (epi)=ec′ilog (epi)
(26)
因为|CLE(SG)|=|CLE(SG′)|所以
gle(G,SG)=gle(G,SG′)
(27)
同理可得
glv(G,SG)=glv(G,SG′)
(28)
因此定理成立.
定义7.图顶点度映射函数(graph vertex Degree Map function):
(29)
该函数是利用子图中顶点的度信息建立的图不变量.其中G为标签图,SG为G的子图,vi是G中顶点,d(vi)是SG中顶点vi的度,f(d(vi))为SG中顶点vi的函数.其中f映射函数是将具有相同度的顶点映射为同一正整数,比如素数.图顶点度映射函数,简称DM函数.
定理3.若SG和SG′同构,则
dm(SG)=dm(SG′)
(30)
证明:设标签图G有N个顶点,M条边,其中|V(G)|=N,|E(G)|=M.SG和SG′是G的子图.d(vi)是SG中顶点vi的度,d(v′i)是SG′中顶点v′i的度,若SG和SG′同构,则下式相等
dm(SG)=dm(SG′)
(31)
若SG和SG′同构,则SG中顶点vi,SG′中顶点v′i分别一一对应,且顶点的度相等,有等式(v1)=d(v′1),d(v2)=d(v′2),d(vi)=d(v′i),令f映射函数是将具有相同度的顶点映射为同一正整数,比如素数.
f(d(v1))=f(d(v′1))
(32)
f(d(v2))=f(d(v′2))
(33)
…
f(d(vi))=f(d(v′i))
(34)
则
(35)
dm(SG)=dm(SG′)
(36)
但两图图同构也有可能度分布不相同,所以DM函数值是判断图同构的非充分条件.由上述讨论可知DM函数值是判断图同构的必要非充分条件,所以是图不变量.
本文提出了基于GL函数值和DM函数值的GLI索引,该索引可以用于分布式条件下.由定理2和定理3可知,GL函数值和DM函数值相同是图同构的必要条件,所以用GL函数值和DM函数值作为子图的索引值,对子图进行分组.若有两个子图的GL函数值和DM函数值都分别相等,则把这两个子图分到同一组中.因为应用GL函数值和DM函数建立索引的过程类似,因此以GL函数为例进行介绍.GLI索引如图3所示.在图3中(a)图为图G,(b)图为根据其子图GL函数值构建的索引.
3.3 图索引算法BGLI
算法1.BGLI
输入:图G,SG_list子图列表
输出:GLI索引
1 初始化GLI索引,GLI为空字典
2 ForSGiin SG_list:
3 Key=根据GL函数和DM函数计算SGi的索引值
4 If Key not in GLI:
5 Then初始化SG_Vec子图向量,放入SG
6 Else SG_Vec =GLI[Key] 找键为Key的子图向量
7 IfSGiin SG_Vec:
8 ThenSGi对应的同构图计数加1
9 Else 在SG_Vec中初始化SGi
10 Return GLI索引
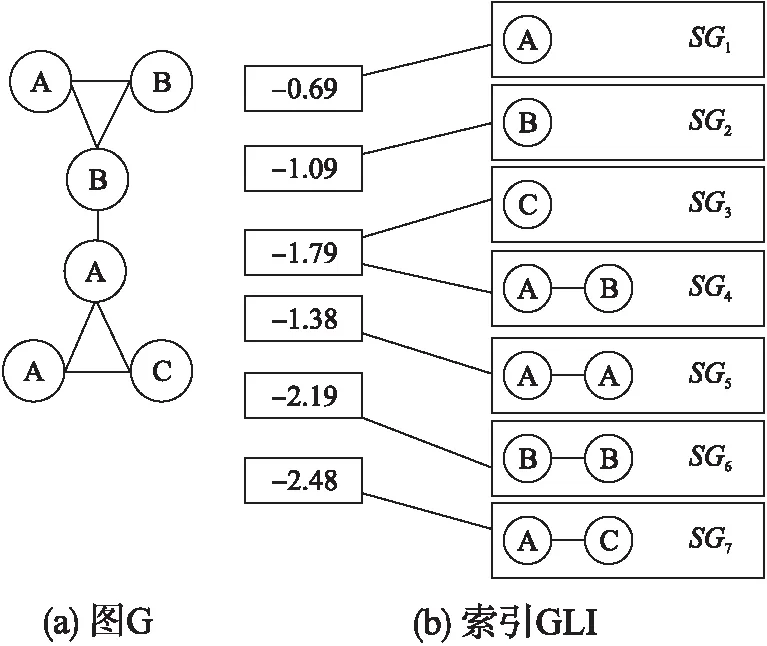
图3 图索引示例Fig.3 Index of graph example
BGLI算法的输入为图G,SG_list子图列表,其中子图列表是在图G中通过采样获得的样本.GLI索引是3层的森林结构.GLI索引的第一层和第二层形成了键值对(key value)字典结构,其中,键是子图SGi的GL函数值和DM函数值,在BGLI算法第3行计算;值是具有相同GL函数值和DM函数值的子图向量SG_Vec,在BGLI算法第4~10行计算.GLI索引的第二层和第三层也是键值对字典结构,其中,键是第二层中子图向量SG_Vec中的子图;值是该子图的计数和该子图邻接字典,即由哈希列表实现的邻接列表.
3.4 子图分布算法ESGS
计算子图分布问题有两个技术难点.其一是,当数据规模过大时,会导致较高时间复杂度,针对小规模数据的算法将难以处理海量数据.其二是,计算子图分布过程中会有大量的子图数据存放在内存当中,这些中间运算结果数据十分庞大.而基于分布式框架Spark的分布式算法能利用集群资源快速处理海量数据.
ESGS算法是基于Spark的分布式算法,因此ESGS算法的计算流程也必须符合Spark的MapReduce计算模型流程,所以ESGS算法分为map过程和reduce过程,下面分别对ESGS算法的map过程和reduce过程详细说明.
下面介绍ESGS算法的map过程,该过程主要负责将要计算任务分发到集群中每一个负责计算的worker节点中,包括对给定k个n阶的子图采样,建立延迟采样列表,根据BGLI算法对子图列表中的子图分类计数并构建GLI索引.
算法2.ESGS-Fun-Map
输入:阶数n,图G,采样个数max_k
输出:被索引的子图数据GLI_data
1 初始化当前采样数k,初始化SG_list延迟采样子图列表
2 While k 3 初始化当前采样子图SGi数的顶点集合vs={} 4 根据随机游走选取顶点并放入vs中 5 根据顶点集合vs中的顶点提取子图SGi 6 将SGi放入SG_list延迟采样子图列表 7 k++ 8 调用算法 BGLI(G,SG_list) 9 Return GLI_data 算法ESGS-Fun-Map中2到7行是图采样过程,该图采样过程是基于随机游走的.图采样过程有两个条件,其一,若顶点集合vs为空且vs中的顶点数小于n,则随机选取第一个顶点v,然后将顶点v放入顶点集合vs.其二,若顶点集合vs非空且vs中的顶点数小于n,则在邻居顶点集合nvs中随机选取一个顶点,然后将其放入顶点集合vs.根据上述顶点选取的方法保证了采样的子图SGi是连通图.该过程并不会真正在map过程全部发生,其第6行是构建延迟采样子图列表,该延迟采样子图列表会记录采样的条件和随后的行为,直至reduce函数触发Spark提交作业完成. 下面介绍ESGS算法的reduce过程,该过程主要负责将集群中每一个负责计算的worker节点中数据回收与合并. 算法3.ESGS-Fun-Reduce 输入:被索引的子图数据GLI_src和 GLI_dec 输出:合并后的被索引的子图数据GLI_dec 1 For Key in GLI_src: 2 If Key not in GLI_dec: 3 Then在GLI_dec加入新数据,其键为Key 4 value为GLI_src 对应的SG_Vec 5 Else 合并GLI_src与GLI_dec具有相同Key的 6 SG_Vec,由相近频率子图开始图同构测试, 7 直到对全部子图测试完毕. 8 If未找到同构子图 Then 插入 GLI_dec 其中伪代码第5到7行是优化的关键,该过程是数据回收合并阶段,集群中每一个负责计算的worker节点,都采集了相同数量的子图样本并依照索引对子图进行了分组,同一组的子图都具有相同的GL函数值和DM函数值,在同一组的子图已经无法按照上述函数值进行区分,必须进行图同构测试.为提高计算速度,提出了依子图频度搜索及合并子图的策略.该策略过程先依频率对子图排序,然后测试频率相近的子图,再测试频率差异大的子图,直到测试完毕. 该策略假设对独立同分布的两组样本,当采样足够大时,同构的子图在这两组样本中的频率应相近或相同.设有两个负责计算的worker节点,都采集k个样本,返回两组子图记为SG_Vec1与SG_Vec2,令每一个子图的频率为随机变量,则由大数定律可知随样本量增大频率会逼近其概率,则在SG_Vec1中任意取一个子图sg1,其频率为sg1f,若在SG_Vec2中有与sg1同构的子图sg2,则当样本量足够大时,sg2的频率sg2f应与sg1f相近或相同.根据上述讨论可知,在上述情况下合并子图时,应先测试频率相近的子图,进而避免无效的图同构测试. BGLI与ESGS算法需要计算分以下几个部分(1)计算图G的各个标签频率,设N=|V(G)|,其中N为图G的顶点个数,则需要计算N次.(2)根据GL函数和DM函数对k个子图计算检索,需要2k次.(3)设k为子图个数,c为索引类别个数,λ为同一索引检索到的子图个数,则k=cλ,则k个子图需要计算kλ2n!次.则计算量总计为N+2kn+kλ2n!,其中N+2kn远远小于kλ2n!,所以ESGS算法的时间复杂度是O(kλ2n!).其中根据实验观察发现,当无标度网络中的顶点标签分布服从参数为1.1的泊松分布时,λ一般小于5. 实验在一台基本配置为:CPU AMD Athlon(tm)II X4 605e Processor、内存4G、64G硬盘的PC上进行、操作系统Fedora 23、Python 3.4.3 、Spark-2.0.2-bin-hadoop2.7、Java 1.8.0_60.为了验证(1)n阶标签零模型用于图分类的有效性.(2)根据n阶标签零模型计算信息提取比可以间接确定合适的样本数量减少冗余计算.(3)基于n阶标签零模型的ESGS算法提取的子图向量化后作为分类特征进行图分类的正确率.分别进行三组实验. 卡方检验实验要验证的是: 1)根据标签零模型计算的子图分布可以判断图不同构. 2)对比标签零模型与Graphlet模型在判断图不同构方面的差异显著性水平. 用于卡方检验的数据,是由文献[9]的模拟数据生成器生成的两个图,这两个图都是无标度网络,其中模拟数据生成器的参数设置为:顶点数n为1000、随机添加新边数m为2、添加新边后形成的三角形概率p分别为0.1和0.5.模拟数据生成器生成的图并无标签,所以使用泊松分布生成标签,其中泊松分布的参数为1.1. 图4 卡方检验对比Fig.4 Comparison of chi2 testing 卡方检验对比的实验结果如图4,图中Graphlet曲线是根据Graphlet模型计算的子图分布进行的卡方检验值的曲线,ESGS曲线是根据标签零模型计算的子图分布进行的卡方检验值的曲线.横坐标为样本量,纵坐标为显著水平,显著水平代表的是两分布为同一分布的概率,接近1表示相同,接近0表示不相同.待检测的数据是两个不同构的图,通过各自的子图分布检验两个图不同构. 由图4可知,随着样本量增加,Graphlet和ESGS显著水平波动性下降,其中ESGS显著水平下降更快,当样本量增加到50至100时,ESGS显著水平已经迅速下降到0.05左右,并且较为稳定,而Graphlet还在剧烈波动.当超过100后ESGS基本稳定在0左右. 卡方检验实验结果分析:造成显著水平剧烈波动的原因分两方面,一方面,当样本量小于50时,根据随机采样得到的子图数量和种类差异都比较大,导致子图分布收敛性不好,以至于Graphlet和ESGS显著水平剧烈波动.另一方面,当样本量大于50时,因为Graphlet模型只考虑图的拓扑信息不考虑顶点和边的标签信息,提取出用于区分图的特征较少,导致显著水平剧烈波动.而ESGS不仅考虑图的拓扑信息还考虑顶点和边的标签信息,提取出用于区分图的特征相对较多,相对较多特征使得子图分布检验更容易判断出两图是不同构的,结果表现在ESGS显著水平波动较小. 在当前的试验条件下,上述实验结果表明:(1)根据标签零模型计算的子图分布能够判断图不同构.(2)ESGS的显著水平下降更快且相对稳定,说明用标签零模型比Graphlet模型在判断图不同构方面的差异显著性水平上更好. 信息提取比实验要验证的是:(1)子图总体分布信息熵的上限是存在的,其上限是正态分布的熵值.(2)计算信息提取比可间接确定样本量,避免样本量过多造成冗余计算. 图5 熵曲线和信息提取比Fig.5 Entropy curve and information extraction ratio 用于信息提取比实验的数据和上文的卡方检验实验数据相同.信息提取比实验结果如图5,在图5中的(a)到(d)图为从数据中分别对3到6阶各自采样的子图样本的熵曲线图.其中,横坐标为采样数量,单位为子图个数,纵坐标为熵值,底数为e,单位为奈特nat;图中Hpe、Hpn、Hq分别为指数分布熵曲线、正态分布熵曲线、样本分布熵曲线,其中指数分布、正态分布的参数都是通过样本统计量均值、方差和参数上下界估算的.图5中的(e)到(h)图为从数据中分别对3到6阶各自采样的子图样本的信息提取比曲线图,其中横坐标为采样数量,纵坐标为信息提取比r,Hper为以指数分布为上限的信息提取比熵曲线,Hpnr为以正态分布为上限的信息提取比熵曲线. 实验结果分析: 1)可以观察到给定均值和方差的情况下,随阶数增大,样本熵曲线与正态分布熵曲线接近速度最快,而且相对于样本熵与指数分布的熵偏离更小,正态分布的熵值是样本分布的熵值上界.随阶数增高,信息提取比熵曲线逐渐稳定,以正态分布为上限的信息提取比高于以指数分布为上限的信息提取比,这进一步证明了正态分布的熵值比指数分布的熵值更接近样本分布的熵值,所以正态分布的熵值可以近似替代总体分布的极限熵.样本分布的熵值与正态分布的熵值接近速度最快,但依旧有发散趋势,说明正态分布并非总体分布. 2)结合信息提取比实验和上文的卡方检验实验结果分析,可发现当样本量为50以下时信息熵增长最快,此时显著水平剧烈波动,当样本量为50到200时,信息熵增长趋于平缓,信息提取比处于90%到98%之间,此时显著水平也趋于0.显著水平接近0表明两图不同构. 在当前的试验条件下,通过本实验可以得出结论: 1)从熵极限角度看,正态分布的熵是总体分布的上限,但总体分布并非正态分布.因此可以使用正态分布的熵近似替代总体分布的极限熵计算信息提取比. 2)通过对信息提取比计算可以间接确定样本的数量,避免样本量过多造成冗余计算. 本实验验证在不同数据集下,基于n阶标签零模型的ESGS算法提取的子图向量化后作为分类特征进行图分类的正确率. 本实验使用的数据集是由美国国家癌症研究院(NCI)公开的两组基准数据,包括NCI1数据集和NCI109数据集,NCI提供的两组基准数据来自于抗肿瘤活性预测任务.这两组基准数据分别代表两组可能致癌物的数据集,致肺癌物质和致卵巢癌物质.每一种物质表示为一个图,若癌症检测为阳性则为1,否则为0.如图6和图7所示,图中横坐标为分类使用的方法,纵坐标为正确率. 图分类的实验结果如图6和图7,在图6和图7中Graphlet代表的是根据Graphlet模型提取特征后应用于各分类算法的实验结果.图中PGD代表的是根据PGD算法提取特征后,应用于各分类算法的实验结果.图中ESGS代表的是ESGS算法根据标签零模型提取特征后,应用于各分类算法的实验结果.图中ESGS_gl代表的是ESGS算法近似计算版,其中提取特征为图似然函数值分布,应用于各分类算法的实验结果.图6和图7中分类方法分别为,基于伯努利模型的贝叶斯分类算法bernoulliNB,基于多项式模型的贝叶斯分类算法MultinomialNB,支持向量机分类算法clf_svm.其中clf_svm_ch2代表的是数据经过卡方校验的方法进行特征选取后,进行支持向量机分类算法计算. 实验结果分析:由图6和图7可知,Graphlet模型的正确率最低,随子图顶点个数增加,正确率有所提升.PGD算法的正确率有所提高,而应用标签零模型计算的ESGS算法正确率最高.即使是当ESGS算法仅计算了图似然函数值分布,对应的分类正确率也比PGD算法的要好. 图6 NCI1数据分类对比Fig.6 NCI1 data classification and comparison 其中支持向量机的正确率提高最为显著,这是由于支持向量机在处理线性不可分数据的方法决定的.支持向量机会通过核函数将输入的低维空间数据映射到高维特征空间中,然后在其中构造出最优分离超平面,把低维空间中不好分的非线性数据分开.显然当对同一组数组,提取的分类特征越多,就越容易形成高维空间,从实验结果看,在这样的高维空间更容易对数据分类. 图7 NCI109数据分类对比Fig.7 NCI109 data classification and comparison Graphlet模型提取的分类特征最少,所以正确率最低.PGD算法的正确率有所提高,这是因为PGD算法提取的分类特征包含了Graphlet模型中所不包含的非连通子图.ESGS_gl代表了当ESGS算法仅计算图似然函数值分布时,忽略了部分结构信息,导致分类特征减少,正确率稍低.ESGS算法提取的分类特征虽然是连通子图,但包含了子图中顶点的标签信息,其分类特征最多,所以正确率最高. 首先,用实验验证了n阶标签零模型用于图分类的有效性.其次,通过实验的结果验证了子图总体分布信息极限熵值的上限是正态分布的熵值,计算信息提取比可以间接确定样本的数量,避免样本量过多造成冗余计算.最后,在NCI1数据集和NCI109数据集上的实验验证了,基于n阶标签零模型的ESGS算法提取的子图向量化后作为分类特征可以提高图分类的准确性. 为提高子图分布算法用于图分类的准确性,本文构建了n阶标签零模型,该模型同时考虑图的拓扑结构信息和图的标签信息,增加了图分类的特征.证明和验证了n阶标签零模型用于图分类的有效性.借鉴信息熵,对子图分布进行了量化分析.针对计算子图分布时需要反复多次进行图同构测试的问题,本文提出了索引算法BGLI和子图分布算法ESGS并在spark上实现,降低了时间复杂度.通过实验验证了,基于n阶标签零模型的ESGS算法提取的子图作为分类特征可以提高图分类的准确性. 本文在计算子图分布时,计算的是全部子图的分布,覆盖面虽然全面,但计算量大.因为在图分类时,不同类别的图,可能具有共同的子图,而这部分子图作为共有特征,分类意义不大.所以下一步的工作是,整合子图分布到图分类算法中,进一步提高图分类的准确性,减少计算量. : [1] Lam W W M,Chan K C C.A graph mining algorithm for classifying chemical compounds [C].IEEE International Conference on Bioinformatics and Biomedicine,2008:321-324. [2] Przulj N,Corneil D I.Modeling interactome scale-free or geometric [J].Bioinformatics,2004,20(18):3508-3515. [4] Ahmed N K,Neville J,Rossi R A,et al.Efficient graphlet counting for large networks [C].IEEE International Conference on Data Mining,2015:1-10. [5] Elenberg E R,Shanmugam K,Borokhovich M,et al.Beyond triangles:a distributed framework for estimating 3-profiles of large graphs [C].Proceedings of the 21thACM SIGKDD International Conference on Knowledge Discovery and Data Mining,2015:229-238. [6] Tan Shan-wang,Huang Guo-xun.The limit theorem of probability distribution for some subgraphs in random complete graphs [J].Journal of Guangxi University Natural Science Edition,1991,16(3):12-18. [7] Newman M,Guo Shi-ze,Chen Zhe.Networks:an introduction [M].Beijing:Oxford University Press,Inc,2014. [8] Mahadevan P,Krioukov D,Fall K,et al.Systematic topology analysis and generation using degree correlations [C].ACM Special Interest Group on Data Communication Computer Communication Review,2006,36(4):135-146. [9] Holme P,Kim B J.Growing scale-free networks with tunable clustering [J].Physical Review E,2002,65(2):026107. 附中文参考文献: [6] 谭尚旺,黄国勋.随机完全图中某些子图的概率分布极限定理 [J].广西大学学报自然科学版,1991,16(3):12-18. [7] 马克·纽曼,郭世泽,陈 哲.网络科学引论 [M].北京:电子工业出版社,2014.3.5 算法性能分析
4 实验分析
4.1 实验1.卡方检验实验

4.2 实验2.信息提取比实验

4.3 实验3.分类实验


4.4 实验总结
5 总结和展望

