利用BP神经网络分析检测网络时序型隐信道

张宇飞，沈 瑶，杨 威，肖汉，黄刘生

1(中国科学技术大学 苏州研究院，江苏 苏州 215123)2(中国科学技术大学 软件学院，江苏 苏州 215123)3(中国科学技术大学 计算机学院，合肥 230026)

1 引 言

隐信道技术是近年来发展起来的一种新型的隐秘通信技术.它利用网络通信机制中的漏洞，秘密地嵌入隐蔽信息，从而绕过网络中的安全检查机制，达到隐秘传输的目的.相比传统的加密技术，隐信道技术在隐藏传输信息的内容的同时，还隐藏了传输信息的行为，因而具有更强的隐蔽性.随着密码学和密文破解技术的发展，加密技术的安全性正在受到挑战，而对于隐信道技术的防范措施的研究工作目前尚处于起步阶段.一旦隐信道技术被不法分子掌握，隐信道技术结合木马、病毒等传统的攻击手段将会对信息安全和个人隐私保护造成极大的威胁.因此对于隐信道检测技术的研究是有意义的.

人工神经网络是通过模拟生物神经系统工作原理而建立的一种计算模型.通过神经网络可以使计算机拥有思考和分析问题的能力.善于处理非线性分类问题是神经网络的主要特征之一.因此，笔者将尝试把神经网络模型引入到隐信道检测工作中，以克服已有检测技术对于非线性分类问题的局限性，同时为检测模型赋予自适应、自学习正常信道数据特征的能力.

本文主要贡献如下：

1)提出了基于BP神经网络的时序型隐信道检测模型，详细介绍了检测模型的体系结构设计.

2)解决了已有算法对于非线性分类情景的局限性和检测窗口大小设定无确定标准的问题.

3)编码实现检测模型，并通过实验对检测模型的性能和检测效果进行评估，实验证明，利用神经网络结合已有算法可以达到更好的检测效果.

本文其余部分的组织结构如下：第2部分主要对相关技术的已有的研究成果进行简要总结；第3部分详细说明基于BP神经网络的时序型隐信道检测模型的体系结构；第4部分说明检测模型在实现过程中的相关细节，主要通过实验给出测模型中的相关参数设定；第5部分说明实验设计和对实验结果的分析；第6部分最后做出全文总结.

2 相关工作

2.1 隐信道

网络隐信道技术是指利用网络中的正常通信信道构建的用于隐秘传输的信道.隐信道的概念最初由Lampson于1973年提出[3，9].

按照隐秘信息的存储载体，网络隐信道可以被划分为网络存储型隐信道和网络时序型隐信道[13].其中存储型隐信道利用网络数据包中的冗余字段存储隐秘信息；而时序型隐信道则将隐秘信息存储在数据包的时间间隔中.时序型隐信道具有构建简单、隐蔽性强的特点，不同类型的时序型隐信道的区别主要在于编码规则，目前较为成熟的时序型隐信道构建方法主要有：IPCTC[1，10]、TRCTC[4]、JitterBug[6]、MBCTC[5]等.

时序型隐信道的检测主要基于对待测数据进行统计特征分析，在时序型隐信道中，由于数据包时间间隔被人为地操纵，其数据包时间间隔一定会表现出不同于正常数据的统计特征.通常考察的统计特征有：均值、方差、标准差、熵值.目前较为成熟的时序型隐信道检测算法有：随机性检测算法[1]、ε相似度算法[1]以及CCE算法[2].以上三种算法均采用单一阈值作为算法最终结果的判定标准，下文中可以看到该判定标准在非线性分类的问题中表现不佳，笔者将通过引入BP神经网络来改善这一缺陷.

2.2 神经网络

人工神经网络(Artifitest Neural Network，ANN)又称为连接模型(Connection Model)，或简称为神经网络(Neural Network)，是一种模仿动物神经网络的行为特征，进行信息处理的计算模型.利用神经网络，可以为机器赋予感知和思考的能力.神经网络模型可以用一个带边权的有向图来描述.图中的点被称为“神经元”，边上附有权值.神经网络是一个分层的结构，输入层用于读取数据的输入，各个神经元对输入数据进行相关处理后，将处理结果传入到各个隐层的神经元中，在具体实现中，隐层部分可以有多层，逐层神经元对数据进行处理后，将结果传至相对于当前层的下一层中，所有隐层的神经元对收到的数据进行处理后，将处理结果传入输出层的神经元中，最后输出层处理数据后，输出处理的结果.在实际应用中，根据神经元之间的关联关系和图中边权的设定方式的不同，可以得到不同的神经网络的组织方式，其中较为成熟的是反向传播神经网络(Back Propagation Neural Network)，简称BP网络.BP网络中各层神经元采用全互连接的方式进行关联，同时采用梯度下降法在训练过程中对网络进行反馈调节，通过反复训练和反馈调节的过程使网络达到较为完美的分类效果.

神经网络模型中的每一个神经元都被赋予了一个非线性的激活函数，通常情况下，激活函数设定为sigmoid函数，其表达式如下：

(1)

激活函数使得网络分析处理数据的过程中可以引入非线性因素，因而神经网络具有善于处理非线性分类问题的优势[12].

3 检测模型的设计

在隐信道检测工作中引入BP神经网络的目的是通过BP神经网络来克服已有检测算法在非线性划分情况下的局限性.笔者通过实验发现，前文中提到的3种时序型隐信道检测算法对于正常信道和隐信道的区分能力已经达到了较为可观的水平，然而，三种算法均采用单一阈值比对的方式考察算法的输出结果，进而得到最终的检测结果.单一阈值会将算法输出值域划分为2个子区间，分别对应正常信道和隐信道.然而笔者通过实际实验发现，对于某些实验数据，正常数据和隐信道数据将会把算法输出值域划分为3个子区间，而正常数据对应的是为于中间位置的子区间，此时，不论如何设定参考阈值，都无法达到较好的检测效果.而这种实验情况就是非线性划分的情况，因此单一阈值的判定标准有一定的局限性，基于以上因素，本文提出基于BP神经网络的时序型隐信道检测模型，基本设计思路是：将已有的检测算法的输出结果看作数据的某种特征，然后将特征值作为BP神经网络的输入，通过BP网络对数据特征进行分析，得到最终的检测结果.另外，笔者还发现，在利用3种已知算法进行实验的过程中，检测窗口大小的设定缺乏统一的标准，因此，在我们的检测模型中，将使用每一种算法在多个不同的检测窗口下对待测数据提取特征，以得到更充分的数据特征信息.检测模型的体系结构可以用图1来描述：

图1 基于BP神经网络的时序型隐信道检测模型Fig.1 Detecting model based on BP neural network

整个检测模型可以分为2个子模块，特征提取模块提取数据的特征；特征分析模块则利用BP神经网络对提取的特征进行分析，得到最终的检测结果.

特征提取模块采用已有检测算法对待测数据进行特征提取，这里设计为树形结构，图中的每个节点称为“特征提取单元”，每个特征提取单元都具有自己的检测窗口大小，位于树形结构较高层的特征提取单元的检测窗口值是与其相关联的低层特征提取单元检测窗口大小的总和.这样的设计的好处是高层提取单元在计算输出结果时可以利用低层特征提取单元的输出结果，从而提高模块的计算效率.在设计阶段，该模块部署了ε相似度算法和CCE算法两种已知特征.

特征提取工作完成后，特征分析模块分析提取到的特征，得到最终的检测结果.该模块采用BP神经网络来实现.其中输入层接收的就是特征提取模块得到的特征数据.这里需要说明的是，虽然特征提取模块以树形结构呈现，并不是位于顶层的特征提取单元的输出结果才会输入到特征分析模块，各个层次的特征提取单元的计算结果均有可能作为该模块的输入，这样就保证了提成分析模块可以对待测数据多个不同的检测窗口值下的特征进行全面分析.特征分析模块的输出层将直接给出最终的检测结果.

4 检测模型的实现

为了测试检测模型的性能和检测效果，这里利用Java和C语言编程实现检测模型，其中特征提取模块利用C语言编程实现，主要实现检测算法；特征分析模块则利用Java编程完成，二者的数据利用利用文本文件I/O进行传送.

4.1 对照算法原理和参数设定

下文中笔者将采用对照实验的方式对检测模型的性能和效果进行评估.作为对照组的算法，笔者设定为部署在特征提取模块中的两个已知算法，这里的参数设定会同时应用于对照组和特征提取单元.这样，对照组的数据处理方式和特征提取单元基本相同，进而便于分析BP神经网络在隐信道检测工作中的影响力和作用.

4.1.1ε相似度算法原理和参数设定

首先介绍ε相似度算法的基本原理：

1)对待测数据以递增的顺序排列，记排序后的序列为{p1，p2，…，pwinSize}.

其中winSize为检测窗口的大小.

2)计算相邻数据之间的相似度，得到相似度序列为{s1，s1，…，swinSize-1}，其中：

(2)

3)统计{s1，s1，…，swinSize-1}中小于参数ε的数值所占的比例，得到算法输出结果similarity：

(3)

4)比较similarity和给定的阈值similarity0，如果similarity>similarity0，表明待测数据包含隐信道，否则，待测数据为正常数据.

算法部署至特征提取单元中后，算法中的步骤(4)将会略去，得到的结果similarity将输入值特征分析模块进行分析.

通过上述步骤可知，这里需要确定参数有筛选参数ε和阈值参数similarity0.Cabuk对相似度算法的测试中将参数ε设定为0.005、0.008、0.01、0.02、0.03和≥0.1共6种不同的值，并将算法检测的阈值设定为μ+σ、μ+1.5σ、μ+2σ、Max共4种不同的值，其中μ、σ、Max分别表示相似度算法检测合法数据所得结果的均值、标准差以及最大值.Cabuk对于上面每一种和阈值的组合进行了测试.根据作者给出的实验结果，当检测阈值设定为μ+σ和μ+1.5σ时，对于每一种参数的设定，检测效果都比较好.此时，对于隐信道的检测可以达到10%以下的漏检率，对于正常信道的检测则可以达到30%以下的误检率.我们的实验设定参考Cabuk的实验过程，将参数设定为0.02，阈值则设定为μ+1.5σ.通过对正常数据的测试，我们相似度算法的对照实验中的测试阈值设定为0.973.测试结果高于此阈值时被认为可能包含隐信道.因此，这里的参数设定结果为

ε=0.02

(4)

similarity0=0.973

(5)

4.1.2 CCE算法原理和参数设定

CCE算法通过评估待测数据的熵率来判定其中是否包含隐信道.信息熵(Entropy)是一种对随机变量随机程度的度量，最初由Shannon于1948年提出[7].而熵率(Entropy Rate)则是一组随机变量熵值的变化率，它反映了多个随机变量之间的关联程度.对于某个随机变量X，其熵值记作EN(X)，对于一组随机变量构成的一维向量X，其熵率记作：ER(X)，其计算公式分别是：

(6)

(7)

可以看到熵率是一个极限定义，为了能通过有限的测试数据得到熵率的估计值，Gianvecchio[2，11]提出了CCE算法，利用修正条件熵(Corrected Conditional Entropy)来对熵率进行估计，Gianvecchio提出的修正条件熵的计算公式如下：

CCE(Xn)=CE(X1，X2，…，Xn)+perc(Xn)·EN(X1)

(8)

其中，其中Xn表示长度为n的随机变量的序列，CE(X1，X2，…，Xn)表示X1，X2，…，Xn的条件信息熵，perc(Xn)则表示测试数据中所有唯一的n长度序列占所有n长度序列的比例，EN(X1)就是随机变量X的熵值.此时，对熵率的估计值，就是选择不同的n值得到的CCE(Xn)的最小值.得到待测数据的熵率估计值后，和给定的阈值CCE0进行比较，测试结果低于CCE0表明待测数据中包含隐信道.

以上为CCE算法的基本原理.在算法实现过程中，我们仅仅选择少数具有代表性的n值进行计算，进而对熵率进行粗略的估计.因此，对于CCE算法，需要确定的参数为检测序列的长度n以及检测阈值CCE0.笔者通过实验发现，正常数据的CCE计算结果大约为0.439，同时，基于算法效率考虑，我们确定最长检测序列的长度为10，即：

CCE0=0.439

(9)

n=10

(10)

4.2 特征提取模块的实现

特征提取模块读取原始的待测数据，通过特征提取单元按照已有部署的检测算法的计算规则提取不同检测窗口下的特征数据.因此特征提取模块的实现中涉及到了整个模块检测窗口大小(记作：winSize)和各个特征提取单元检测窗口的大小以及多个特征提取单元的关联关系的确定问题.笔者将通过相关实验来得到特征提取模块的最优实现方案.

首先，整个模块的检测窗口大小决定了整个检测模型的计算开销和结构的复杂程度，显然，输入数据的规模越大，特征提取模块需要的特征提取单元的数目就越多，特征分析模块中的神经元的数目也就越多；然而，检测窗口如果过小则会有更大的特征丢失的可能性，影响检测模型对于数据的特征学习.笔者参照隐信道检测方面已有的相关文献，并结合以上因素考虑，确定整个模型的检测窗口大小为2000，即：

winSize=2000

(11)

对于特征提取单元的设定，涉及到了多个不同的检测窗口的特征提取，首先，我们为特征提取单元确定检测窗口，这里记作win={w1，w2，…，wcnt}，其中cnt为拥有不同检测窗口大小的特征提取单元的数目，显然，对于任意的窗口值wi，满足：

wi≤winSize

(12)

笔者认为，为了避免冗余数据，这里对win的设定标准为：尽可能使的检测算法对每个wi产生差别较大的结果，从而提取到更为完备的数据特征.

接下来通过实验来确定特征提取单元的检测窗口大小，这里笔者通过抓包程序抓取了10000条正常信道中的数据包间隔数据.设定窗口值为50，100，150，…，2000，统计这些窗口之下ε相似度算法和CCE算法的计算结果.实验结果如图2、图3所示.

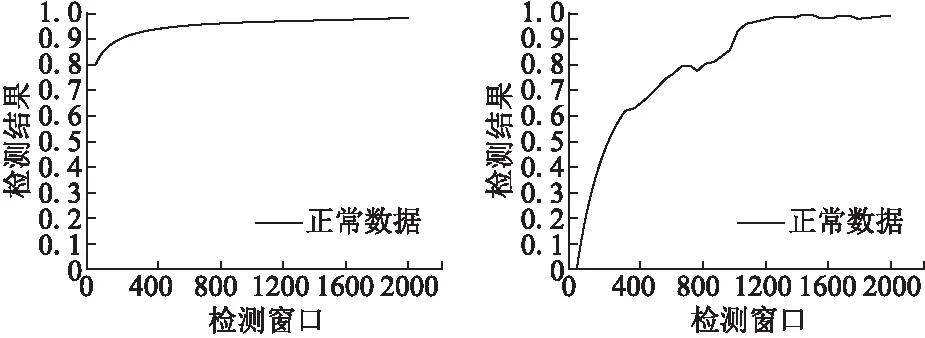
图2 不同检测窗口下的ε 相似度算法输出结果 图3 不同检测窗口下的CCE算法输出结果

观察图2可以发现，由于笔者所处的网络环境较为稳定，网络传输过程中的传输速率较为均匀，因此，数据包间隔数据的波动性很小.当检测窗口大于600时，相似度小于参数ε的数据的比例已达到95%，此时再增加窗口大小，算法结果变化很小.

观察图3可以发现，检测窗口小于1200时，改变检测窗口大小将对CCE算法的计算结果产生较大的影响.相比图2的结果，可以看出，CCE算法对于数据特征的变化更为敏感，相比之下，ε相似度算法在处理数据过程中对数据进行了排序处理，排序过程丢失了原有数据中相邻数据之间的关联关系，这也是造成图2实验结果的主要因素.

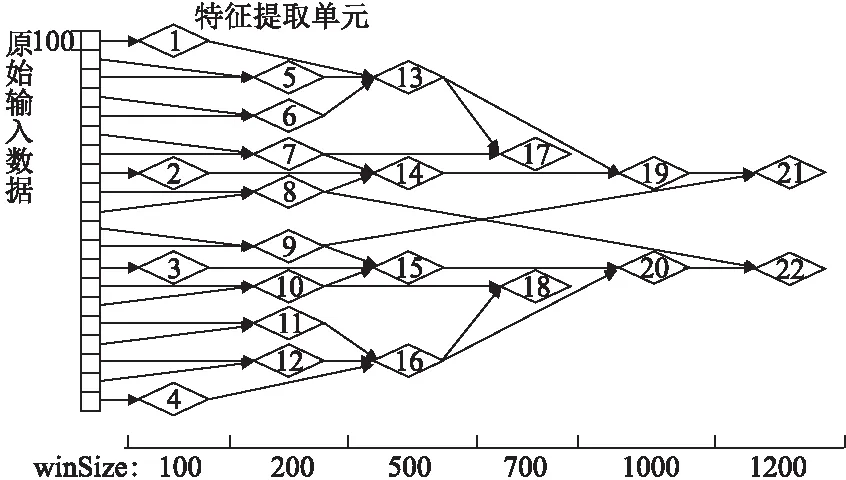
图4 特征提取模块体系结构设计Fig.4 Architecture of module of Feature collecting

综合以上实验结果，笔者认为，在设定特征提取单元的检测窗口大小时，应该主要在[50，1200]范围内选取，小于50的检测窗口笔者也不建议选取，因为过小的窗口值将会使特征提取过程对于数据中的噪声数据过于敏感.

最后，笔者决定，选择的窗口大小有100、200、500、700、1000以及1200，其中，窗口值200部署在8个特征提取单元中，窗口值500部署在4个特征提取单元中，窗口值700部署在2个特征提取单元中，窗口值1000和1200也各部署在2个特征提取单元中，将窗口值100部署在4个特征提取单元中.其中窗口值为200的6个特征提取单元以及窗口值为500、700、1000、1200的所有特征提取单元作为当前模块输出结果的特征提取单元，共有16个.即：

win={100，200，500，700，1000，1200}

(13)

决定窗口值后，就可以决定特征提取单元之间的关联关系，可以用图4来描述.其中灰色的特征提取单元作为当前模块的输出结果.图中的箭头标明了各个特征提取单元之间的关联关系，高层特征提取单元将调用低层特征提取单元的输出结果进行计算.

4.3 特征分析模块的实现

特征分析模块利用BP神经网络对提取到的特征进行分析，得到最终的检测结果.该模块在实现过程中涉及到的参数值有：输入输出数据规模、隐层数、各隐层节点数、以及各个边权的初始权值.本节将详细介绍以上参数的设定方案.

4.3.1 输入与输出

记输入层和输出层数据规模分别为cin和cout，这里输入输出数据规模即为输入层和输出层包含神经元的数目.特征分析模块的输入数据是特征提取模块的输出数据，前文中已经说明，特征提取模块对原始数据的处理后，将得到数据规模为16的特征数据，因此，当前模块输入数据规模为16，即：

cin=16

(14)

输出层得到的是检测模型的最终输出结果.前文中笔者已经提到，目前已有的检测算法得到的检测结果均为一个表示待测数据中是否包含隐信道的一个布尔值，而实际应用中，待检测的数据往往是正常数据和隐信道数据的混合数据.因此，仅仅用单一的布尔值来表示检测结果还不够准确.这里将输出结果设定为多维数据，表示当前检测数据中包含隐信道的概率，笔者将输出规模设定为10，即：

cout=10

(15)

此时，对于某次检测，如果输出数据中有k维数据表示当前数据包含隐信道，则当前待测数据包含隐信道的概率就是k/10，检测结果可以精确到0.1.

4.3.2 隐层设定

隐层设定包括隐层层数的设定和各隐层包含的神经元数目的设定.这里记隐层数目为h，各隐层包含的神经元的数目为c={c1，c2，…，ch}.

从某种程度上，BP神经网络包含的隐层层数决定了网络对数据分类的精度.网络层数越多，网络模拟复杂分类情况的能力就越强，但网络层数的增多还意味着网络包含更多的神经元以及网络计算中更多的时间开销.已有研究表明，包含单隐层的三层BP神经网络已经具备拟合任何一个闭区间内的连续函数的能力，包含两个隐层的BP网络可以适用于任何形式的分类问题[8].

这里笔者通过实验来决定隐层数目，通过程序生成10000条包含IPCTC隐信道的数据包时间间隔数据，结合上文中抓取的正常信道数据，通过特征提取模块得到对应的特征数据后，在给定隐层层数的情况下，对特征分析模块训练5000次，考察网络在训练后的准确率.从理论上讲，增加隐层数目可以提高网络分类的准确率.

实验中考虑到输入数据规模和网络效率，笔者设定隐层数为1～10进行了实验.在当前实验中，各层神经元数目暂时按照Kolmogorov原理的标准：对于第i层隐层中包含的神经元数目Ni，其大小满足如下的关系：

Ni=2Ni-1+1

(16)

同时，各个神经元关联的初始权值暂定为0.

实验结果如图5所示.

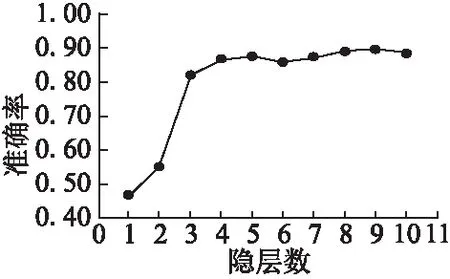
图5 不同隐层数下的检测准确率Fig.5 Detecting rate in different hide layers number setting

观察图5可以看出，当隐层数大于3时，检测率可以达到80%的水平，同时继续增加隐层数时，检测率将会继续提升，但提升幅度明显减小.因此，这里笔者将当前模块中的隐层数设定为3，即

h=3

(17)

确定隐层数后，接下来确定各层包含的神经元数目.在上面的实验中，我们已经根据Kolmogorov原理确定了各层的神经元数目，对于三隐层的网络，各隐层神经元数目为33、67和135.然而，此结果未必是最优的设定方案，在这里笔者以一种动态调整的方式确定各层的最优神经元数目.具体思路为：通过训练数据对网络反复训练，并动态地记录每一次训练后可以达到的检测率，当检测率低于某个阈值r1时，说明网络中节点数目还不足以完美拟合当前的数据，此时，向包含神经元数目最少的隐层中添加一个神经元；当检测率高于某个阈值r2时，说明当前网络对数据拟合的程度较高，可以适当减少节点改善网络计算效率，此时从包含神经元数目最多的隐层中减少一个神经元.对于阈值r1和r2的设定，由于上文实验结果中隐层数为3时，检测率大约为80%，这里的阈值以(80±10)%来确定，即

r1=70%

(18)

r2=90%

(19)

通过实验，我们得到的各隐层包含的神经元数目为：64、72、98，即

c={64，72，98}

(20)

4.3.3 神经元关联与初始权值

BP神经网络以全互连接的方式进行关联，即每一层中的每一个神经元都和下一层中的所有神经元进行关联.而对于每条关联的初始权值，已有研究表明，设定初始权值使得神经元在计算过程中从激活函数变化速率最快的位置开始可以达到较好的训练效果，因为此时对网络进行反馈调节时，神经元的状态变化最为明显，网络的收敛速度也最快.

我们的BP网络中采用的激活函数为sigmoid函数，该函数在坐标原点位置的斜率是最大的，因此合适的初始权值为0，这一点笔者前前文所述的实验中已经得到了证实.另外，sigmoid函数的表达式前文中式(1)已经给出.该函数的值域为(-1，1)，特征数据输入到当前模块中时，首先要进行标准化处理，即基于以上值域范围对数据进行等比例缩放.

5 实验和结果分析

本节通过实验检验本文提出的检测模型的性能和检测效果.我们首先将分析检测模型在训练阶段的性能，然后通过对照实验来评估检测模型的检测效果.

5.1 隐信道构建原理和实验数据的收集

实验该数据包括训练数据和测数据.这里将通过程序模拟生成3种隐信道类型的数据：IPCTC、TRCTC、JitterBug同时通过抓包程序实时抓包获取正常数据，结合参数设定的不同生成多组数据集，每种数据集包含20000条数据的训练数据和包含100000条数据的测试数据.

5.1.1 IPCTC隐信道原理和实验数据生成

IPCTC的构建原理是：发送方和接收方约定一个时间间隔t，信道建立后，发送发通过控制每一个大小为t的时间区间内是否有数据包发送来决定发送比特0或比特1.接收方对信道进行监控，如果在某个时间区间中抓取到发送方发送的数据包，接收方就接收到了比特1，否则，接收到的数据为比特0.结合笔者的网络环境，这里选择t值为100ms和500ms，构建2个IPCTC隐信道数据集如表1所示.

表1 IPCTC实验数据Table 1 IPCTC testing data

5.1.2 TRCTC隐信道实验数据生成

TRCTC通过模拟正常数据来构建隐信道.其基本原理是：首先对正常数据进行数值采样，然后将采样得到数据划分为S0和S1两个子集，通信过程中，如果需要发送比特0，就从S0中随机选取一个时间间隔作为当前数据包和前一个数据包的时间间隔，否则从集合S1中选择时间间隔数据.按照集合S0和S1线性划分或非线性划分的方式，可以生成不同的TRCTC隐信道数据，显然，非线性划分得到的TRCTC数据具有更强的隐蔽性，但与此同时，信道传输的准确率将会因集合S0和S1的差异变小而有所下降.结合笔者的实验环境，这里以线性划分和非线性划分的方式各生成1组TRCTC数据集.

5.1.3 JitterBug隐信道实验数据生成

JitterBug隐信道的构建原理是：发送方和接收方约定参数w，通过对正常数据进行微调来实现隐秘信息的编码.具体来说，如果要发送比特1，就调整数据包间隔使其可以整除w，否则调整间隔使其不可以整除w，但可以整除w/2.这里笔者设定w值为2，10，50，生成三种JitterBug数据集：

5.2 检测模型的训练性能

得到实验数据后，接下来利用生成的训练数据对检测模型进行训练，上文中在确定隐层层数时进行过类似的实验，而在这里，网络结构已经通过前文所述过程调整至最优状态后，我们再次通过实验测试模型的训练性能.得到的结果见图6.

表3 JitterBug实验数据Table 3 JitterBug testing data

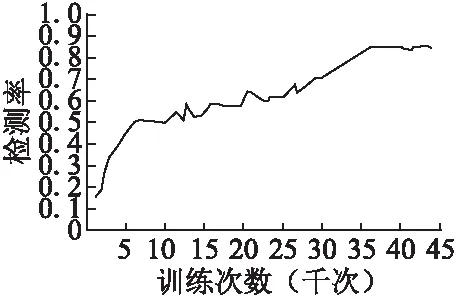
图6 检测该模型训练实验结果Fig.6 Performance of detecting model in training

训练工作共耗时97小时32分59秒，训练次数为44325次.观察图6可以发现当训练次数大于32500次后，网络的检测率开始趋于稳定.这里由于多种隐信道数据的引入，从而增加了训练数据的复杂度，因而，这里实验需要的训练次数远远高于4.3.2节中的实验.实验表明，基于目前的训练数据，检测模块在训练30000次左右后可以基本达到80%的检测率.

5.3 检测模型的检测能力

最后，我们通过对照实验评估检测模型的检测效果，得到的实验结果见表4.

表4 检测率实验结果Table 4 Results of covert channel testing using ε-similarity，CCE and our detecting model

观察表4的实验结果可以发现，本文提出的检测模型在检测率上明显优于两种已有算法.查看文献[1]和文献[2]可以发现，这两种算法的原理均基于“正常信道数据随机性高于隐信道”的假设，同时在进行判定时，均采用单阈值作为参照标准.关于单阈值标准对于非线性分类具有局限性的问题前文已经说明.笔者还在实验中发现，ε相似度算法和CCE算法对于隐信道和正常信道的区分能力是可观的，然而，得到的检测结果却和算法给定的判定标准完全相反，造成此现象的原因可能是笔者所处环境的网络较为通畅，因此，这两种算法所参照的假设也不完全成立，进而再利用算法原有的判定标准进行判定，检测率就会降低.

本文提出的检测模型利用神经网络对已有算法输出结果进行分析后得到检测结果，省去了已有算法单阈值比对的过程，也就避免了已有算法对于非线性划分情况的局限性.另外，本检测模型中对于正常数据的特征通过网络学习得到，而不基于任何假设条件，因此对于不同网络环境具有更强的适应能力.

6 总 结

本文提出了一种基于BP神经网络的时序型隐信道检测方法.在检测模型的设计过程中，结合了两种已有的检测算法，通过引入神经网络模型充分结合并发挥了已有算法对于隐信道的识别能力，同时还克服了已有算法对于非线性分类情况的局限性.实验表明，本文提出的检测方法相比已有算法具有一定的优势.未来的研究工作将主要集中在检测模型结构改进训练性能优化方面.

：

[1] Cabuk S，Brodley C E，Shields C.IP covert timing channels：Design and detection[C].Proc.of the 11th ACM Conf.on Computer and Communications Security，2004：178-187.

[2] Gianvecchio S，Wang H.Detecting covert timing channels：an entropy-based approach[C].Proceedings of the 14th ACM Conference on Computer and Communications Security(CCS′07)，ACM，New York，NY，USA，2007：307-316.

[3] Lampson B W.A note on the confinement problem[J].Communications of the ACM，1973，16(10)：613-615.

[4] Cabuk S.Network covert channels：design，analysis，detection and elimination[D].Dissertation，Purdue University，West Lafayette，IN.，USA，December，2006.

[5] Gianvecchio S，Wang H，Wijesekera D，et al.Model-based covert timing channels：automated modeling and evasion[J].International Symposium on Recent Advances in Intrusion Detection，2008，(5230)：211-230.

[6] Shah G，Molina A，Blaze M.Keyboards and covert channels[C].Conference on Usenix Security Symposium：Conference on Usenix Security Symposium，2006：59-75.

[7] Shannon C.A mathematical thoery of communication[J].Bell System Technical Journal，2014，27(3)：379-423.

[8] Yan Hong，Guan Yan-ping.Method to determine the quantity of internal nodes of back propagation neural networks and Its demonstration[J].Control Engineering of China，2009，16(S1)：100-102.

[9] Biswas A K，Ghosal D，Nagaraja S.A survey of timing channels and countermeasures[M].Acm Computing Surveys,2017,50(1):1-39.

[10] Wang C，Yuan Y，Huang L.Base communication model of covert timing channels[J].Frontiers of Computer Science，2016，10(6)：1130-1141.

[11] Shrestha P L，Hempel M，Frezaei.A support vector machine-based framework for detection of covert timing channels[J].IEEE Transactions on Dependable and Secure Computing，2016，13(2)：274-283.

[12] Zhang De-hui，Zhang De-yu，Liu Qing-yun，et al.BP neural network optimized by improved PSO[J].Computer Engineering and Design，2015，36(5)：1321-1326.

[13] Wei San-qiang，Yang Wei，Shen Yao.A covert communication method based on reliable packet ordering[J].Journal of Chinese Computer Systems，2016，37(1)：124-128.

附中文参考文献：

[8] 严 鸿，管燕萍.BP神经网络隐层单元数的确定方法及实例[J].控制工程，2009，16(S1)：100-102.

[12] 张德慧，张德育，刘清云，等.基于粒子群算法的BP神经网络优化技术[J].计算机工程与设计，2015，36(5)：1321-1326.

[13] 魏三强，杨 威，沈 瑶.一种基于可靠包排序的隐秘通信方法[J].小型微型计算机系统，2016，37(1)：124-128.