扩散的分子通信模型的多跳可靠性和时延分析
程 珍,赵慧婷,林 飞,雷艳静
(浙江工业大学 计算机科学与技术学院,杭州 310023)
1 引 言
分子通信作为一种新型的网络技术,它使得纳米网络的实现成为可能[1].分子通信[2]是纳米机器之间一种新型的通信方式,以生物化学分子作为信息载体,通过分子在生物环境中扩散的方式进行相互通信[3].分子通信技术有望在有前景的领域中得到应用,例如,药物传递[4]以及纳米体域网[5]等.
针对分子通信的生物兼容性、不可靠性的特点[6],较多的研究者对不同的分子通信模型的性能进行了详细的分析.Atakan等人[7]设计了可移动的ad hoc分子纳米网络模型并分析该纳米网络如何达到较高的吞吐量.Akan等人[8]首次提出基于信息分子的概率密度通信模型,并利用简单异或网络编码机制减少了时延开销.在此基础上,Atakan等人[9]优化了该模型的信道容量.Balasubramaniam等人[10]深入分析了基于细菌分子通信网络在网格拓扑和随机拓扑结构下的多跳路由机制.Walsh 等人[11]研究了将病毒粒子作为信息载体的多跳分子通信模型,分析了病毒分子纳米网络多跳传输的可靠性,并将病毒粒子的扩散、吸收、衰变的过程作为影响多跳链路可靠性的因素进行考虑.论文[12]研究了不考虑码间干扰的、基于概率密度的分子通信模型在多播场景下的可靠性和时延分析.
扩散的分子通信模型中[13],发送方纳米机器通过释放一定数量的分子到生物环境中表示信息的传输,分子遵循布朗运动规则扩散,并随机到达接收方纳米机器.到目前为止,还没有文献研究扩散的分子通信模型在考虑码间干扰情况下的可靠性和时延分析,本文填补了此空缺.本文与已有工作[11,12]比较如下:
从分子通信模型上比较,论文[11]考虑了基于病毒的分子通信模型,可以看到可靠性和时延的计算主要依赖于分子浓度公式,影响可靠性和时延的参数是不同的.论文[12]中的可靠性和时延研究主要是基于概率密度的分子通信模型,但该论文中的分子通信模型没有考虑分子在前面时隙对当前时隙的码间干扰.而本文研究了基于概率密度的分子通信模型并考虑了发送方纳米机器在前面所有时隙释放的分子对当前时隙的码间干扰情况.
从仿真结果上比较,分别与基于病毒的分子通信模型[11]和不考虑码间干扰的分子通信模型[12]相比,在相同的通信场景下,扩散的分子通信模型达到相同的可靠性所花费的时延开销大大降低.
2 系统模型
本节介绍本文所考虑的二进制分时隙的、扩散的分子通信模型.在该模型中,发送方纳米机器TN(Transmitter Nanomachine)和接收方纳米机器RN(Receiver Nanomachine)分别表示该模型中的发送方和接收方.假设TN与RN在时间上完全同步,同时假设所有分子被接收的事件发生在离散时间点.分子传输时间被划分为大小相同的时隙,记为T=NTs.T为信息传输的时间,Ts为每个时隙持续时间,N为所划分的时隙的个数.在二进制扩散的分子通信模型中,输入输出均为二进制信息比特1或0,待发送的二进制比特信息被编码在分子上,这里用两种不同类型的分子A1和A2分别表示比特1和0的发送.A1和A2类型的分子均包含要到达的RN的地址信息.
分子通信模型的基本过程包括信息的编码、发送、传输、接收和解码五个步骤[14].当TN在时间T内发送信息比特1或0,则TN在每个时隙开始时释放M个相应A1类型或A2类型分子到传输信道中,分子一旦被释放在生物环境中,会进行自由扩散.这些分子可能在当前时隙到达RN,也可能会在之后的时隙到达RN.当被RN接收后会立即被吸收,不再存在生物环境中.图1展示了分子在TN和RN间的传输信道中的传输过程.这里M=8,N=4.

图1 分子在TN和RN间扩散的时序图Fig.1 Sequence diagram of molecules diffuse between TN and RN
我们考虑一维环境中的分子扩散情况,在分子传输及扩散过程中,描述任一分子从发送方纳米机器i到达接收方纳米机器j的时间t的概率密度函数[15]为
(1)
其中,dij表示两个纳米机器之间的距离,D是生物环境的扩散系数.因此,fij(t)的累积分布函数Fij(t)可以用于描述一个分子在t时刻之前到达接收方纳米机器的概率,表示如下:
(2)
在分子接收过程中,RN通过收到的分子类型判定当前时隙收到的比特为1或0.当RN成功收到TN发送的分子,则RN必须发送M个确认分子给TN.确认分子的类型不同于发送1或0所对应的A1或A2类型,但它们有相同的扩散、被吸收等性质.当TN没有成功收到RN发送的确认分子,TN需要重传相同数量的同类型分子给RN.当RN在设置的超时时间内没有成功收到TN发送的分子,TN同样需要重传相同数量的同类型分子给RN.
3 扩散的分子通信模型的多跳可靠性和时延分析
在本节中,我们给出了单链路和多跳链路通信场景下,扩散的分子通信模型的可靠性和时延的数学表达式;此外,研究了当链路传输失败时,如何利用重传机制保证该模型中信息的可靠传输.
3.1 单链路的可靠性和时延
假设发送方纳米机器i在时隙k发送一个比特1或0的概率相同,记为β.令Pij(k,n)表示发送方纳米机器i第k个时隙发送的分子在第n个时隙被接收方纳米机器j收到的概率.则有:
Pij(k,n)=β[Fij((n-k+1)Ts)-Fij((n-k)Ts)],k (3) 特别地,当k=n时, Pij(n,n)=βFij(Ts) (4) 因此,发送方纳米机器i发送的分子在第n个时隙没有被接收方纳米机器j收到的概率pij(n)为: (5) 单链路的可靠性定义为接收方纳米机器j在T时刻之前即N个时隙内至少收到一个分子的概率,用γij表示,即为: (6) 其中,M表示发送方纳米机器i在每个时隙开始时发送的分子数.可以看到,发送方纳米机器i每个时隙发送的分子个数、两个纳米机器之间的距离、生物环境的扩散系数等参数对链路的可靠性有着十分重要的影响. 我们关注接收方纳米机器j首次成功收到分子的情况.用Psuccess,ij(m)表示在前面(m-1)个时隙接收方纳米机器j都没有成功收到一个分子,并在第m个时隙首次成功收到一个分子的概率.计算公式如下所示: (7) 链路的传输时延τij定义为发送方纳米机器i发送的分子首次成功被接收方纳米机器j收到的第m个时隙内,分子被成功收到的概率之和达到该链路可靠性的一半时所需的最小时间.表示如下: (8) 根据[8],我们将链路ij间总的时延τtotal,ij定义为传输时延τij以及为释放信息分子而消耗的准备时延τprepare之和,即: τtotal,ij=τij+τprepare (9) 当发送方纳米机器i发送一定数量的分子到生物环境中,由于分子扩散的随机性,接收方纳米机器j可能会产生没有分子到达的情况.因此,需要考虑用上节介绍的重传机制来保证链路的可靠传输.我们定义:当单链路传输失败,需要进行重传时该链路的可靠性Pre,ij为第fij次传输时RN至少收到一个分子的概率为: (10) 其中,fij表示最大重传次数.链路ij间的可靠性γij可以通过(6)得到.此时链路的总时延Tre,ij为: Tre,ij=τprepare+τij+τACK,ijfij (11) 其中,τACK,ij为链路的超时时间,链路的传输时延τij可以通过(8)得到. 多跳链路的通信场景如图2所示.其中,发送方纳米机器TN、接收方纳米机器RN以及中继纳米机器A、B等一系列纳米机器组成多跳拓扑结构.TN发送分子,通过纳米机器的转发,最后到达RN.我们将多跳拓扑结构看成由多个单链路组成,即中继纳米机器A既是TN的接收方纳米机器,同时又是下一跳纳米机器的发送方纳米机器,而分子只能在相邻的纳米机器间进行传输.在每个时隙的开始,TN会发送相应类型的分子给中继纳米机器A.当A至少收到一个从TN释放的分子后,会给TN发送确认分子表示已成功收到信息,同时通过收到的分子类型进行解码,将解码后的信息对应到相应类型的分子并转发给下一个纳米机器.如果在超时时间内TN没有收到来自A的确认分子,那么TN重新发送相同数量的同类型的分子给A.根据以上传输过程,我们可以推导出扩散的多跳分子通信模型的可靠性和时延分析情况. 图2 多跳链路的拓扑结构Fig.2 Topology of multihop link 假设s为多跳链路上W个纳米机器的集合,Bs为每条单链路的可靠性集合,Ds为每条单链路的时延集合.例如,假设多跳链路由三跳单链路构成,即W=4,则s=[1,2,3,4]表示多跳链路s中存在纳米机器1,2,3,4,分子可通过纳米机器1经由纳米机器2和3传递到纳米机器4.此时,该链路可靠性的集合记为Bs=[γ12,γ23,γ34],时延的集合为Ds=[τ12,τ23,τ34].W个纳米机器构成的多跳链路的可靠性γs和时延τs为 (12) (13) 当链路传输失败时,令fs表示相邻纳米机器组成的链路重传次数的集合.则此时多跳链路的可靠性Pre,s和时延Tre,s分别为 (14) (15) 其中,Bre,s和Dre,s分别表示考虑重传时单链路可靠性和时延的集合,Pre,ij和Tre,ij分别通过公式(10)(11)获得,其中的数据来源于Bs和Ds,节点ij间的最大重传次数fij取自fs集合. 本节将通过Matlab实验仿真展示扩散的分子通信模型中,不同参数,包括纳米机器之间的距离d、生物环境的扩散系数D、每个时隙发送的分子个数M对单链路及多跳通信场景下的可靠性和时延的影响. 本小节中,我们考虑单链路场景包括成功链路以及失败链路下的可靠性和时延分析. 4.1.1 成功单链路的可靠性分析 在图3和图4中,我们通过公式(6)分别描绘了生物环境的扩散系数D以及TN和RN之间距离d在取不同值的情况下,链路可靠性随着每个时隙发送的分子个数增大的变化趋势.参数设置如下:N=20,Ts=30s.此外,在图3中,d=200μm;在图4中,D=7μm2/s. 图3 D取值不同时单链路可靠性与M的关系Fig.3 Reliability of single link is varying with M for different values of D 由图3和图4可知,在其它参数保持不变的情况下,单链路的可靠性会随着每个时隙发送的分子个数增大而提高,但到达一定数量后不再增大.这是由于在生物环境中的分子个数变大导致分子到达接收方纳米机器的概率变大,从而使得单链路的可靠性增大.另一方面,在图3中,当生物环境的扩散系数增大时,该链路的可靠性会随之增大.扩散系数越大意味着分子运动越快,在相同的时间内到接收方纳米机器的概率就越大.而在图4中,保持其它参数不变,减小两个纳米机器之间的距离会增大单链路的可靠性.两个纳米机器之间的距离越小,使得相同数量的分子在相同时间内更容易到达接收方纳米机器,从而提高了该链路的可靠性. 图4 d取值不同时单链路可靠性与M的关系Fig.4 Reliability of single link is varying with M for different values of d 4.1.2 成功单链路的时延分析 在图5和图6中,我们通过公式(9)分别描绘了生物环境的扩散系数D以及TN和RN之间距离d在取不同值的情况下,单链路的时延随着每个时隙发送的分子数量增大的变化趋势.参数设置如下:N=50,Ts=30s.此外,在图5中,d=200μm,在图6中,D=7μm2/s.根据[8],每释放10个信息分子需要消耗准备时间τprepare为10-3s.当每个时隙发送的分子个数增大,时延会随之减少.这是由于生物环境中的分子个数增多导致分子到达接收方纳米机器的概率增大,从而所需的时延就会减少.在图5中,随着生物环境的扩散系数的增大,分子运动变快,分子到达接收方纳米机器的时延减少.在图6中,随着两个纳米机器之间距离的增大,分子到达接收方纳米机器的时延增大. 图5 D取值不同时单链路时延与M的关系Fig.5 Delay of single link versus M for different values of D 图6 d取值不同时单链路时延与M的关系Fig.6 Delay of single link versus M for different values of d 4.1.3 失败单链路可靠性和时延分析 图7和图8是失败单链路场景下,链路可靠性和时延在重传机制下与每个时隙发送的分子个数之间的关系.参数设置如下:d=200μm,D=3.6μm2/s,N=35,Ts=25s.默认在纳米机器1和2之间进行传输,f12表示最大重传次数,图中省略下标,之后相关图不另行说明.随着重传的次数增加,链路的可靠性增加,链路的时延也相应地变大.当分子个数为50时,重传一次的可靠性增大不到0.2,但时延差不多是原来的3倍.虽然重传一次所花费的时延代价比较高,但是在分子纳米通信中保证通信的可靠性非常重要,因此,在可以容忍的范围内以时延为代价提高链路的可靠性是值得的. 根据图2,我们假设一维生物环境中有四个纳米机器,包括发送方和接收方纳米机器,以及两个中继纳米机器.同时假设每两个纳米机器之间的距离相等,并假设每个纳米机器只能与相邻的纳米机器通信.图9和图10分别展示了多跳链路通信场景下的可靠性和时延与每个时隙发送的分子个数之间的变化关系.参数设置如下:在图9中,D=3.6μm2/s,N=20,Ts=40s,d=200μm.在图10中,D=10μm2/s,N=50,Ts=20s,d=200μm.根据公式(12)、(13)、(14)、(15)可以得到多跳链路的可靠性和时延的仿真结果. 图7 f取不同值时单链路可靠性与M的关系Fig.7 Reliability of single link versus M for different f 图8 f取不同值时单链路时延与M的关系Fig.8 Delay of single link versus M for different f 图9 f取不同值时,多跳链路可靠性与M的关系Fig.9 Reliability of multihop link versus M for different f 图10 f取不同值时,多跳链路时延与M的关系Fig.10 Delay of multihop link versus M for different f 多跳链路和单链路一样,当每个时隙发送的分子个数增大时,链路的可靠性增大,时延减小.另外,在图9和图10中,我们可以看到当最大的重传次数增大时,链路的可靠性和时延也相应地增大. 本节主要考虑在单链路通信场景中,在参数设置相同值的条件下,与[11]和[12]的分子通信模型中达到相同可靠性所需时延的对比. 图11展示的是扩散系数D分别取2μm2/s、3.6μm2/s和7μm2/s的情况下,单链路可靠性与时延间的关系.这里,参数设置如下:M=1500,d=200μm,N=20.由图11可知,当D=3.6μm2/s时,链路的可靠性达到0.9所需要的时延约为0.15小时.在参数包括释放总的分子个数,D和d设置相同值的情况下,当达到相同的可靠性0.9时,论文[11]中所需时延为5小时,论文[12]中所需时延为2.5小时.因此,与[11]和[12]中的分子通信模型相比,在相同的通信场景下,扩散的分子通信模型达到相同的可靠性所花费的时延开销大大降低. 图11 单链路时延与可靠性的关系Fig.11 Relationship between delay and reliability for single link 在本文中,我们考虑了发送方纳米机器在前面所有时隙释放的分子对当前时隙的码间干扰,分析了扩散的分子通信模型在单链路及多跳链路下的可靠性和时延.特别地,对于失败链路,我们利用重传机制保证信息传输的可靠性.在此情况下,也分析了失败的单链路和多跳链路下的可靠性和时延.随着每个时隙发送的分子个数的增加,生物环境的扩散系数越大,两个纳米机器之间的距离越小,可靠性会提高,同时,时延会减小.此外,重传可以大大增加链路的可靠性,与此同时,传输时延也会增大.值得一提的是,分别与[11]和[12]相比,对于相同的通信场景,扩散的分子通信模型达到相同的可靠性所花费的时延开销大大降低. : [1] Akyildiz I F,Brunetti F,Blázquez C.Nanonetworks:a new communication paradigm[J].Computer Networks(Comput.Netw.),2008,52(12):2260-2279. [2] Nakano T,Eckford A,Haraguchi T.Molecular communication[M].London:Springer,2006. [3] Jiang C,Chen Y,Liu K J R.Inter-user interference in molecular communication networks[C].IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP),2014:5725-5729. [4] Yoo J W,Irvine D J,Discher D E,et al.Bioinspired,bioengineered and biomimetic drug delivery carriers[J].Nature Reviews Drug Discovery(Nat.Rev.Drug Discov.),2011,10(7):521-535. [5] Peng Mu-gen,Yin Bo-nan,Wang Wen-bo.Bacteria-based molecular communication and body-area nano-networks[J].Journal of Beijing University of Posts and Telecommunications(JBUPT),2016,39(1):1-11. [6] Nakano T,Moore M.Molecular communication paradigm overview[J].Journal of Next Generation Information Technology(JNIT),2011,2(1):9-16. [7] Guney A,Atakan B,Akan O B.Mobile ad hoc nanonetworks with collision-based molecular communication[J].IEEE Transactions on Mobile Computing(IEEE Trans,Mobile Comput.),2012,11(3):353-366. [8] Unluturk B D,Malak D,Akan O B.Rate-delay tradeoff with network coding in molecular nanonetworks[J].IEEE Transactions on Nanotechnology(IEEE Trans.Nanotechnol.),2013,12(2):120-128. [9] Atakan B.Optimal transmission probability in binary molecular communication[J].IEEE Communications Letters(IEEE Commun.Lett.),2013,17(6):1152-1155. [10] Balasubramaniam S,Lio P.Multi-hop conjugation based bacteria nanonetworks[J].IEEE Transactions on Nanobioscience(IEEE Trans.Nanobiosci.),2013,12(1):47-59. [11] Walsh F,Balasubramaniam S.Reliability and delay analysis of multihop virus-based nanonetworks[J].IEEE Transactions on Nanotechnology(IEEE Trans.Nanotechnol.),2013,12(5):674-684. [12] Cheng Z,Zhu Y,Chi K,et al.Reliability and delay analysis of multicast in binary molecular communication[J].Nano Communication Networks(Nano Commun.Netw.),2016,9(1):17-27. [13] Singhal A,Mallik R K,Lall B.Performance analysis of amplitude modulation schemes for diffusion-based molecular communication[J].IEEE Transactions on Wireless Communications(IEEE Trans.Wireless Commun.),2015,14(10):5681-5691. [14] Yang Cheng-feng,Lin Lin,Wang Jian-dong,et al.The analysis of model for emission and reception in molecular communication[J].Journal of Computer Simulation,2015,32(2):210-214. [15] Karatzas I,Shreve S E.Brownian motion and stochastic calculus[M].New York:Springer,1988. 附中文参考文献: [5] 彭木根,尹博南,王文博.细菌分子通信和身体域纳米网络[J].北京邮电大学学报,2016,39(1):1-11. [14] 杨成凤,林 林,王建东,等.分子通信的发送和接收模型的分析[J].计算机仿真,2015,32(2):210-214.3.2 多跳链路场景下的可靠性和时延分析

4 仿真结果
4.1 单链路场景下的可靠性和时延分析



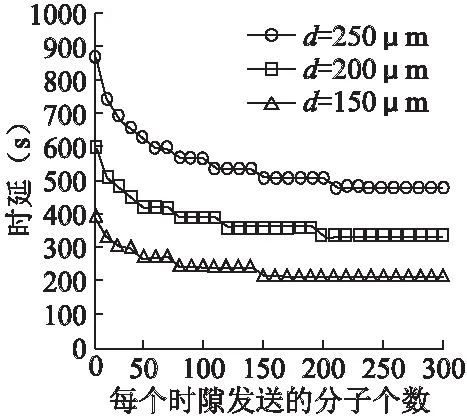
4.2 多跳链路的可靠性和时延分析

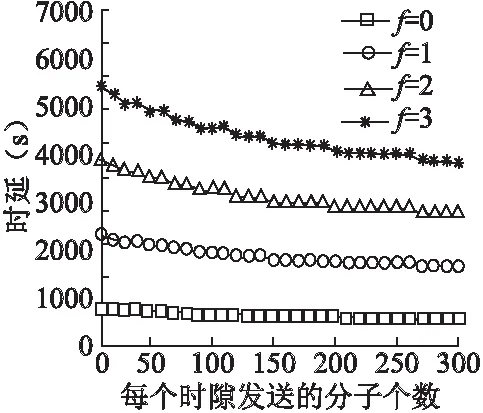

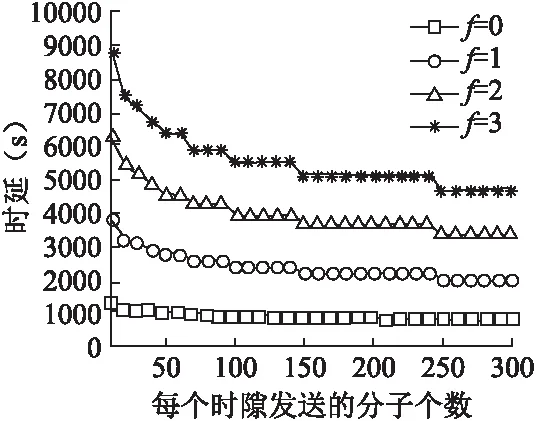
4.3 与其它分子通信模型的对比

5 结束语

