直觉模糊信息系统下的三支决策模型
刘久兵,张里博,周献中,黄 兵,李华雄
1(南京大学 工程 管理学院,南京 210093)
2(南京审计大学 审计科学研究院,南京 211815)
1 引 言
上世纪九十年代,Yao等将经典Pawlak粗糙集上、下近似集的代数包含关系放宽为概率包含关系,并引入贝叶斯最小风险决策理论,提出决策粗糙集模型[1].该模型不再将保持决策知识与数据的精确一致性作为唯一目标,而更加关注不同决策错误所带来的不同风险代价,使得模型对风险代价高的错误分类决策具有代价敏感性[2].决策粗糙集导出的分类规则具有正域、负域和边界域的三区域特征,因此被称为三支决策粗糙集,其对应的决策也称为三支决策[3].决策粗糙集的三支决策语义优于传统的二支决策,这与人类智能处理复杂决策问题的方法是一致的,适合在决策信息不明确、可用信息不充分的背景下获取有效的评估决策知识,并作出具有最小风险代价的评估决策[4].因此,决策粗糙集广泛应用于垃圾邮件过滤[5]、多属性决策[6,7]及不完备信息决策表[8,9]等领域.
模糊集是Zadeh教授于上世纪中期提出的用于处理不精确、不确定问题的经典数学方法[10].其采用适当的主观隶属函数,通过模糊集的运算和变换,实现对主观模糊概念的有效刻画[11].由于模糊集仅有模糊对象的隶属度指标,难以完整刻画人们对模糊概念的主观认识.1986年,保加利亚学者Atanassov在对象与集合的关系中增加非隶属度和犹豫度等两方面信息提出直觉模糊集[12].它增加了模糊对象的非隶属度和犹豫度指标,其在表达不确定信息时能更加真实地反映主体对客观事物模糊本质的认识[13].直觉模糊集和粗糙集均为处理不确定、不精确问题的有力工具,若采用直觉模糊集描述主观信息,并且以粗糙集为挖掘和表示知识方法,则可以集成两种理论的优点.
近年来,有关直觉模糊集和粗糙集的集成方法逐渐成为不确定决策与知识发现的研究热点[14,22].2003年,Cornelis等将直觉模糊集与粗糙集相结合,最早提出直觉模糊粗糙集模型[15].2008年,Zhou和Wu从粗糙近似算子角度研究直觉模糊粗糙集模型,提出一般化的直觉模糊粗糙近似算子[16].2010年,张植明等提出基于覆盖的直觉模糊粗糙集模型[17].2011和2012年,黄兵、李华雄等提出基于距离关系的直觉模糊粗糙集方法[18],然后将优势关系引入直觉模糊粗糙集中,提出基于优势-直觉模糊集的粗糙集知识获取方法,并应用于IT项目绩效评估中[19].2013年,Huang等采用粗糙集方法,研究区间直觉模糊信息系统的知识获取与规则提取方法[20].2014年,Huang等将多粒度粗糙集与直觉模糊集相结合,提出多粒度直觉粗糙集模型[21].2015年,Liang和Liu采用直觉模糊数表达决策粗糙集模型的代价函数,提出基于决策粗糙集的直觉模糊三支决策方法[22].
从上述研究现状可知,直觉模糊集、决策粗糙集和三支决策等理论在不确定决策与知识获取等领域引起学者的广泛关注,并在决策分析领域得到成功应用.然而,现实决策问题既依赖于历史的客观数据,又与决策者的主观风险偏好有关,如何将直觉模糊集的主观评判信息与决策粗糙集的客观知识获取过程有效结合,建立评估决策者的合理风险偏好模型,实现多风险偏好的决策评估知识获取,这是本文值得研究的问题.本文给出新的定义,并基于贝叶斯决策过程建立直觉模糊信息系统下的三支决策模型.
2 基本概念及定义.
2.1 直觉模糊数

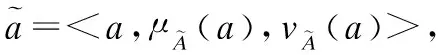
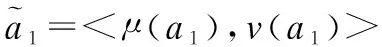
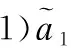

+|π(a1)-π(a2)|)
(1)
(2)
2.2 直觉模糊信息系统

定义3[25].设U为给定论域,一个二元直觉模糊关系R为U×U上的直觉模糊子集,即
R={<(x,y),μR(x,y),vR(x,y)>|(x,y)∈U×U}
(3)
其中μR和vR为U×U→[0,1]上的隶属相关映射和非隶属相关映射,且对任意的(x,y)∈U×U均满足:0≤μR(x,y)+vR(x,y)≤1.特别地,若R满足如下条件:
1)自反性,即对∀x∈U,恒有μR(x,x)=1∧vR(x,x)=0.
2)对称性,即对∀(x×y)∈U,有μR(x,y)=μR(y,x),vR(x,y)=vR(y,x).
则称R为U×U上的二元直觉模糊相容关系.记U上的二元直觉模糊相容关系全体为IFCR(U×U).
3 直觉模糊信息系统下的三支决策模型
3.1 直觉模糊粗糙近似
基于上述定义的直觉模糊数的标准海明距离和相异度,下面给出直觉模糊信息系统对象间关于属性的相容度和相异度定义.
定义4. 设IFSS=(U,C∪D,V,f),R∈IFCR(U×U),∀B∈C.f(x,c)=<μc(x),vc(x)>为对象x在属性c∈B下的直觉模糊属性值,则对象x,y关于属性集B的相容度μR(x,y)和相异度vR(x,y)分别定义为
(4)
其中d(f(x,c),f(y,c))和e(f(x,c),f(y,c))分别表示直觉模糊数f(x,c)与f(y,c)的标准海明距离和相异度.
基于定义3.1易证μR(x,y)和vR(x,y)具有的性质:
性质1. 设IFSS=(U,C∪D,V,f),对任意x,y∈U,c∈B⊆C,则
1)0≤μR(x,y)≤1,0≤vR(x,y)≤1;
2)μR(x,y)=μR(y,x),vR(x,y)=vR(y,x);
3)0≤μR(x,y)+vR(x,y)≤1;
4)若μR(x,y)=1,则vR(x,y)=0;反之,若μR(x,y)=0,则vR(x,y)=1;
5)f(x,c)=f(y,c)当且仅当μR(x,y)=1,vR(x,y)=0;
6)若f(x,c)=<1,0>,f(y,c)=<0,1>,则μR(x,y)=0,vR(x,y)=1.

(5)


定理1. 设R,H∈IFCR(U×U),0≤α≤1,0≤β≤1且满足:0≤α+β≤1,则




证明:

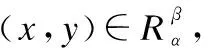



(6)
其中:<α,β>为由阈值对(α,β)构成的常直觉模糊数.
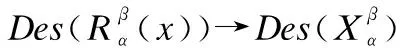

(7)
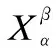
(8)
(9)


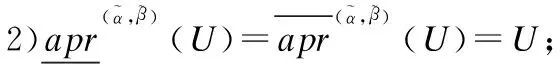

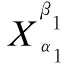
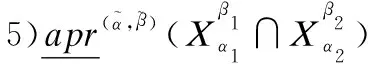
3.2 直觉模糊信息系统下的三支决策模型


表1 直觉模糊风险损失矩阵Table 1 Risk cost matrix of intuitionistic fuzzy decisions
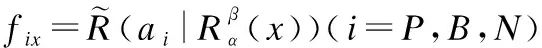


根据基于直觉模糊数的得分函数和精确函数排序法,可先计算直觉模糊风险期望fix(i=P,B,N)的得分函数和精确函数如下:
S(fPx)=μP-vP,H(fPx)=μP+vP;S(fBx)=μB-vB,
H(fBx)=μB+vB;S(fNx)=μN-vN,H(fNx)=μN+vN.
基于上述得分函数和期望函数,可对各期望风险损失fix(i=P,B,N)进行排序,并得到基于直觉模糊风险偏好的三支决策规则先决条件:
C1:S(fPx) 综上给出的决策先决条件,下面构建一种关于直觉模糊风险偏好的三支决策规则: 算法:基于直觉模糊信息系统的三支规则提取算法. 输入:直觉模糊决策系统IFSD=(U,C∪D,V,f),阈值α,β. 输出:对象x∈U的决策规则. 步骤1.式(4)分别计算任意两个对象x,y∈U关于条件属性C的相容度μR(x,y)和vR(x,y). 步骤3.计算对象x∈U在三种行动i={P,B,N}下的期望风险损失fix及其得分函数S(fix)和精确函数H(fix). 步骤4.根据决策先决条件C1-C12和三支决策规则(P)-(N)获得决策规则. 为说明本文方法的有效性,对文献[18]的安全审计风险评估算例进行改编,表2给出一个安全审计风险评估的直觉模糊目标决策系统,审计对象x={x1,x2,x3,x4},条件属性C={c1,c2,c3,c4,c5},其中c1,c2,c3,c4,c5分表表示“优良系统环境”、“较好的系统控制”、“可靠的财务数据”、“可信的审计软件”,“规范运作”等属性,决策属性c6表示“可接受的安全审计风险”.各条件属性取值由审计专家根据审计调查结果并依据自身职业素养综合给出,例如f(x4,c4)=<0.7,0.1> 表2 基于安全审计风险评估的直觉模糊决策系统Table 2 Security audit risk assessment based intuitionistic fuzzy information system 表示70%的审计专家认为被审计对象x4的审计软件可信,10%的专家认为不可信,20%的专家未作出评估.同理,对于决策属性c6如f(x2,c6)=<0.6,0.4>可理解为60%的专家认为被审计对象x2的安全审计风险可接受,40%的专家认为不可接受并在不同状态(安全审计风险可接受和不可接受)采取不同行动的损失值也由专家给定,见表3. 表3 安全审计风险在不同状态采取不同行动的损失矩阵Table 3 Cost matrix of different actions in different states 假设给定的阈值α=0.7,β=0.3,采用本文提出的方法对算例进行决策规则提取,详细步骤如下: 步骤1.计算对象xj,xk间的相容度μR(xj,xk)和相异度vR(xj,xk)(j,k=1,2,3,4;j≠k)如下: μR(x1,x2)=0.7,vR(x1,x2)=0.25;μR(x1,x3)=0.8,vR(x1,x3)=0.2;μR(x1,x4)=0.6,vR(x1,x4)=0.3;μR(x2,x3)=0.7,vR(x2,x3)=0.3;μR(x2,x4)=0.8,vR(x2,x4)=0.15;μR(x3,x4)=0.5,vR(x3,x4)=0.4. 步骤3.计算对象xj在三种行动i={P,B,N}下的期望风险损失fixj及其得分函数S(fixj)和精确函数H(fixj)如下: fPx1=<0.4549,0.5040>,fBx1=<0.5358,0.4642>,fNx1=<0.6825,0.3037>,fPx2=<0.3821,0.5657>,fBx2=<0.5271,0.4729>,fNx2=<0.7172,0.2736>,fPx3=<0.3821,0.5657>,fBx3=<0.5271,0.4729>,fNx3=<0.7172,0.2736>,fPx4=<0.5757,0.4000>,fBx4=<0.5528,0.4472>,fNx4=<0.6000,0.3742>. 进而,计算得相应得分函数如下: S(fPx1)=-0.0491,S(fBx1)=0.0716,S(fNx1)=0.3788,S(fPx2)=-0.1836,S(fBx2)=0.0542,S(fNx2)=0.4436,S(fPx3)=-0.1836,S(fBx3)=0.0542,S(fNx3)=0.4436,S(fPx4)=0.1757,S(fBx4)=0.1056,S(fNx4)=0.4436. 步骤4.根据决策先决条件C1-C12和三支决策规则(P)-(N)获得相应的决策准则如下: 即在给定的阈值α=0.7,β=0.3下,对于对象x1,x2和x3,其审计风险均认为是安全的;而对于对象x4来说,其审计风险需进一步商榷. 基于直觉模糊信息系统提出对象间的相容度和相异度概念,并给出相关的性质.进而定义直觉模糊相容关系下的(α,β)-水平截集和决策目标下的(α,β)-水平截集,并将上述定义及粗糙隶属度概念引入决策粗糙集模型中,结合直觉模糊数的得分函数和精确函数,进而提出一种基于直觉模糊信息系统的三支决策规则提取算法.最后通过算例说明方法的有效性.后续工作将对直觉模糊信息系统的属性约简和规则提取进行深入研究. : [1] Yao Y Y,Wong S K M.A decision theoretic framework for approximating concepts[J].International Journal of Man-machine Studies,1992,37(6):793-809. [2] Yao Y Y.Three-way decisions with probabilistic rough sets[J].Information Sciences,2010,180(3):341-353. [3] Yao Y Y.The superiority of three-way decisions in probabilistic rough set models[J].Information Sciences,2011,181(6):1080-1096. [4] Li H X,Zhou X Z.Risk decision making based on decision-theoretic rough set:a multi-view decision model[J].International Journal of Computational Intelligence Systems,2011,4(1):1-11. [5] Jia X Y,Zheng K,Li W W,et al.Three-way decisions solution to filter spam email:an empirical study[C].Proc of 7th RSCTC,LNCS,Springer,2012,7413:287-296. [6] Liang D C,Witold Pedrycz,Liu D,et al.Three-way decisions based on decision-theoretic rough sets under linguistic assessment with the aid of group decision making[J].Applied Soft Computing,2015,29:256-269. [7] Liang D C,Liu D,Kobina Agbodah.Three-way group decisions with decision-theoretic rough sets[J].Information Sciences,2016,345:46-64. [8] Li H X,Wang M H,Zhou X Z,et al.An interval set model for learning rules from incomplete information table[J].International Journal of Approximate Reasoning,2012,53 (1):24-37. [9] Liu D,Liang D C,Wang C C.A novel three-way decision model based on incomplete information system[J].Knowledge Based Systems,2016,91(C):32-45. [10] Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353. [11] Feng G.A survey on analysis and design of model-based fuzzy control systems[J].IEEE Transactions on Fuzzy Systems,2006,14(5):676-697. [12] Atanassov K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96. [13] Liu H W,Wang G J.Multi-criteria decision-making methods based on Intuitionistic fuzzy sets[J].European Journal of Operational Research,2007,179(1):220-233. [14] Zhang X X,Chen D G,Tsang E.C.C.Generalized dominance rough set models for the dominance intuitionistic fuzzy information systems[J].Information Sciences,2017,378:1-25. [15] Cornelis C,Cock M D,Kerre E E.Intuitionistic fuzzy rough sets:at the crossroads of imperfect knowledge[J].Expert Systems,2003,20(5):260-270. [16] Zhou L,Wu W Z.On generalized intuitionistic fuzzy rough approximation operators[J].Information Sciences,2008,178:2448-2465. [17] Zhang Zhi-ming,Bai Yun-chao.Tian Jing-feng.Intuitionistic fuzzy rough sets based on intuitionistic fuzzy coverings[J].Control and Decision,2010,25(9):1369-1373. [18] Huang Bing,Wei Da-kuan.Distance-based rough set model in intuitionistic fuzzy information systems and its application[J].Systems Engineering-Theory & Practice,2011,31(7):1356-1362. [19] Huang Bing,Li Hua-xiong.Evaluation rules acquisition of performance audit for IT projects in China Based on dominance intuitionistic fuzzy rough set model[J].Computer Science,2011,38(10):223-227. [20] Huang B,Zhuang Y L,Li H X.Information granulation and uncertainty measures in interval-valued intuitionistic fuzzy information systems[J].European Journal of Operational Research,2013,231(1):162-170. [21] Huang B,Guo C X,Zhuang Y L,et al.Intuitionistic fuzzy multi-granulation rough sets[J].Information Sciences,2014,277:299-320. [22] Liang D C,Liu D.Deriving three-way decisions from intuitionistic fuzzy decision-theoretic rough sets[J].Information Sciences,2015,300(C):28-48. [23] Li D F.Some measures of dissimilarity in intuitionistic fuzzy structures[J].Journal of Computer and System Sciences,2004,68(1):115-122. [24] Xu Z S,Yager R R.Intuitionistic and interval-valued intuitionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group[J].Fuzzy Optimization and Decision Making,2009,8(2):123-139. [25] Bustince H,Burillo P.Structures on intuitionistic fuzzy relations[J].Fuzzy Sets and Systems,1996,78:293-303. [26] Yuan Xue-hai,Li Hong-xing,Sun Kai-biao.The cut sets,decomposition theorem and representation theorem of intuitionistic fuzzy sets and interval valued fuzzy sets[J].Science in China Press,2009,39(9):933-945. 附中文参考文献: [17] 张植明,白云超,田景峰.基于覆盖的直觉模糊粗糙集[J].控制与决策,2010,25(9):1369-1373. [18] 黄 兵,魏大宽.基于距离的直觉模糊粗糙模型及应用[J].系统工程理论与实践,2011,31(7):1356-1362. [19] 黄 兵,李华雄.基于优势-直觉模糊粗糙模型的IT项目绩效审计评价规则获取[J].计算机科学,2011,38(10):223-227. [26] 袁学海,李洪兴,孙凯彪.直觉模糊集和区间值模糊集的截集、分解定理和表现定理[J].中国科学 F 辑:信息科学,2009,39(9):933-945.
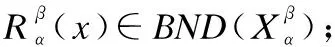

3.3 直觉模糊信息系统下的三支决策规则提取算法

4 算例分析



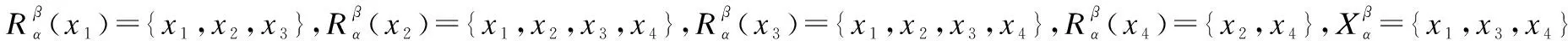
5 总 结

