船舶碰撞引起的自升式海洋平台结构损伤分析

刘洋， 桂洪斌

(哈尔滨工业大学(威海)船舶与海洋工程学院，山东 威海 264209)

0 引 言

随着世界各国对海洋资源开发利用幅度的加大，海洋平台的数量不断增多，船舶与海洋平台碰撞的事故也发生得越来越频繁。TEBBETT[1]对全球100个需要修理的海洋平台的损伤原因进行了分析，发现近25%的海洋平台的结构损伤是由碰撞引起的。船舶与平台碰撞的事故会使平台局部遭受严重的损伤甚至使平台整体被破坏。因此，对船舶碰撞引起的海洋平台的结构损伤分析具有非常重要的现实意义。自升式海洋平台数量在4种主要的海上可移动钻井平台中占比约60%，因此对这类平台碰撞特性的研究就显得尤为重要。

对船舶碰撞海洋平台的问题国内外学者们已经做了很多研究：林一等[2]针对自升式平台的耐撞性问题，准确模拟了船舶与自升式海洋平台碰撞的场景；WOISIN[3]进行了一系列高动能的船舶碰撞模型试验，结果发现船舶的船首形状不同则碰撞力显著不同；AZADI EMAMI[4]研究了船舶的质量和速度等参数对自升式平台损伤的影响；STORHEIM等[5]用非线性有限元法分析了半潜式平台在遭到船舶碰撞后的剩余极限强度；温小飞等[6]通过数值模拟和试验研究提出了关于船舶与海洋平台碰撞问题可行的研究思路；VILLAVICENCIO等[7]通过对加筋板结构的相关试验分析，提出了运用有限元法求解碰撞问题的可行性方案，并且给出了相关碰撞参数的设置要求。

上述研究都没有对船舶不同位置碰撞平台进行比较研究。文献[3]的研究结果表明，对于船首与平台碰撞的情况，船首的形状对平台的损伤特性有很大的影响，因此船的不同位置碰撞平台必然会很大程度上影响平台的结构损伤特性。本文针对船舶不同位置碰撞平台的问题展开研究，涉及的实际情况包括：由于驾驶员操作失误或者在极恶劣海况下过往船舶的船首直接碰撞平台；供应船或铺管船停靠平台时船中与平台相撞；在船舶为避开与平台碰撞而转向的过程中船尾与平台相撞等。本文在验证数值方法正确性的基础上，研究船首碰撞、船中碰撞和船尾碰撞这3种情况下平台的损伤特性，并通过对碰撞结果的对比分析研究船舶的碰撞部位对平台损伤的影响，为平台的损伤评估提供参考。

1 船撞平台问题的计算原理及验证

1.1 计算原理

在总坐标系中，物体的运动微分方程为

(1)

(2)

式(1)和(2)中加速度向量可以通过将结构的剩余载荷矩阵乘以质量阵的逆矩阵得到。线性方程组有解的条件是质量阵为对角阵，从而可求出加速度向量为

(3)

在时间的推进上采用中心差分法可以得到速度向量和位移向量：

v(n+1)/2=v(n-1)/2+an(Δt(n+1)/2+Δt(n-1)/2)/2

(4)

dn+1=dn+v(n+1)/2Δt(n+1)/2

(5)

1.2 数值方法验证

文献[8]对船舶与自升式海洋平台的碰撞系统进行了简化处理，其中将船舶简化为刚性三角楔形锤头，被撞平台简化为撞击区域的直管、T形管和K形管。本文将船舶简化为刚性三角楔形锤头，将被撞平台简化为撞击区域的K形管进行数值方法验证。锤头质量为209.7 kg，冲击速度为6.3 m/s。锤头模型选用四边形壳单元(S4R)，其质量与试验中的相同；其他构件均选用实体单元建模，通过定义全局网格尺寸对各个构件进行网格划分。模型的几何尺寸和全局网格尺寸见表1，材料的应变率与Cowper-Symonds模型[9]一致。

(6)

式中：σ′是在塑性应变率为ε时的动屈服应力；σ是相应的静屈服应力；D和q为应变率常数。

表1 船撞平台有限元模型几何尺寸和全局网格尺寸

陈永念等[10]研究了网格的尺寸对材料失效应变的影响。根据其研究结果和本文有限元模型的网格尺寸，材料的失效应变应为0.35，K形管的材料参数见表2。

表2 K形管材料参数

K形管的各构件之间的连接均设置为理想焊接，模型的边界条件为：弦管和斜撑杆的端板固定；锤头仅保留竖直方向的自由度；锤头与弦管的接触类型为通用接触；摩擦因数为0.3。建立的有限元模型见图1。

图1 锤头撞击K形管的有限元模型

图2为数值模拟与文献[8]的试验所得碰撞力时序曲线的对比图。从图2中可以看出，数值计算得到的碰撞力时序曲线与试验结果基本一致，碰撞力的最大误差为3.24%。这说明本文计算结果的误差控制在合理的范围内，利用数值方法研究此类碰撞问题是可行的。

图2 碰撞力时序曲线对比

2 船撞平台有限元模型

2.1 平台模型

图3是平台的有限元模型。平台为K形桁架式结构，可变载荷为6 500 t(大钩载荷为905 t)，平台桩腿总长为123 m，弦管中心距为10.6 m，节间距为5.44 m，工作水深为80 m，各构件之间均采用ABAQUS的理想焊接。平台模型主要包括主船体和桩腿，主船体质量为16 120 t，由于主船体不直接参与碰撞，只是在碰撞过程中产生动力响应，所以在不改变平台整体重心和惯性矩分布的前提下，对主船体进行了简化处理：只建立主船体的外壳而忽略上层建筑的影响。

图3 平台的有限元模型

平台的桩腿和主船体分别用四边形壳单元(S4R)和三角形壳单元(R3D3)划分：未发生碰撞区域的弦管网格尺寸为1 m，水平撑杆和斜撑杆的网格尺寸为0.5 m；碰撞区域的弦管网格尺寸为30 mm，水平撑杆和斜撑杆的网格尺寸为20 mm；主船体的网格尺寸为2 m。平台的网格总数为193 963个，其中碰撞区域(网格细化部分)的网格数为82 195个。平台桩腿结构的主尺度见表3，平台的有限元模型以及碰撞区域的局部网格放大模型见图3。

表3 平台桩腿结构主尺度

2.2 船舶模型

与平台发生碰撞的船舶类型主要为供给船，其占所报道的发生碰撞事故的船舶总数的78%，而大约95%的供应船的排水量为5 000 t[11]。因此，本文设船舶的排水量为5 000 t，船长为75.5 m，型宽为13.2 m，型深为7.5 m，船尾碰撞方向沿船长方向，碰撞位置与船中的距离为21.83 m。

对船舶的碰撞区域(船首、船中和船尾)进行网格细化，网格尺寸为80 mm。图4a、4b、4c分别为船首、船中和船尾碰撞平台的示意图。

2.3 材料属性

根据设置的平台网格尺寸，平台构件材料的失效应变为0.35，材料的基本参数见表4。因为船舶的相对刚度较大，在碰撞过程中发生变形的主要是平台的桩腿，而且本文主要研究的是平台桩腿的损伤，所以为提高计算效率，将船舶和平台主体简化为刚体。

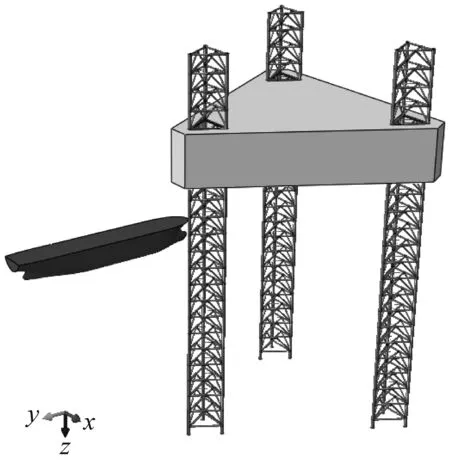
a)船首碰撞

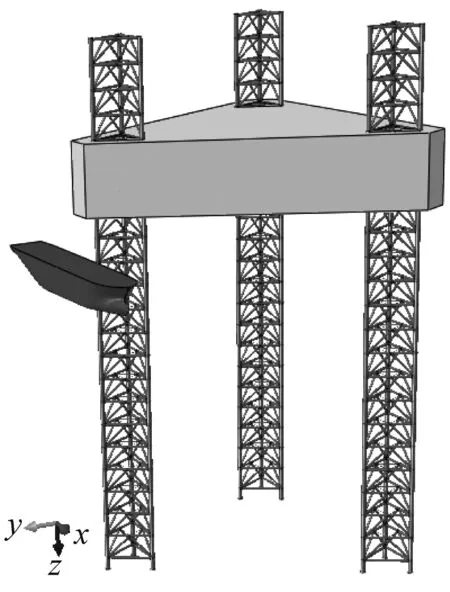
b)船中碰撞

c)船尾碰撞图4 船首、船中和船尾碰撞平台的示意图表4 平台桩腿材料参数

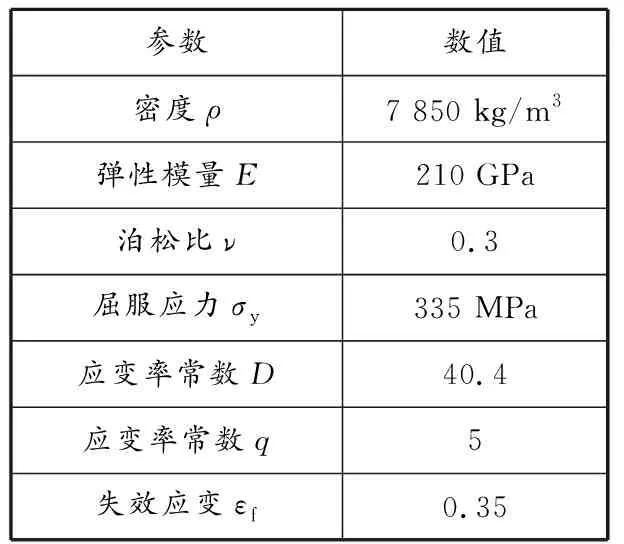
参数数值密度ρ7 850 kg/m3弹性模量E210 GPa泊松比ν0.3屈服应力σy335 MPa应变率常数D40.4应变率常数q5失效应变εf0.35

2.4 碰撞场景的确定

2.4.1 碰撞区域

对于船舶和平台而言，可能发生碰撞的角度很多，但是船舶正撞平台的弦管无疑是最危险的，对平台的损伤也是最严重的，因此本文选择船舶正撞平台的桩腿弦管作为研究工况。

2.4.2 附加质量

对于船舶与平台碰撞过程中附连水的考虑，王自力等[12]通过比较流固耦合法与附加质量法的计算结果，证明了用附加质量法与用流固耦合法得到的仿真结果相近。由于流固耦合法计算效率较低，所以本文选择附加质量法考虑附连水作用的影响。

元良誠三等[13]就附加质量系数进行了一系列模型试验和水动力分析，发现横移运动船舶的附加质量为0.4倍的船体质量，而纵移运动船舶的附加质量为0.1倍的船体质量。因此，当船首碰撞平台时船体的实际质量为5 500 t；当船中或船尾撞击平台时船体的实际质量为7 000 t。

2.4.3 碰撞速度

船舶的碰撞速度有赖于平台附近水域的波高，根据经验[14]，船舶碰撞速度与波高的关系为

v=0.5h

(7)

式中：v为碰撞速度；h为平台附近的最大名义波高。

自升式海洋平台在正常工作时，一般其附近水域的波高为1～4 m，则碰撞速度应为0.5～2 m/s。HARGREAVES等[15]认为2 m/s可以作为碰撞设计时的典型碰撞速度，因此本文在研究船首碰撞和船中碰撞时设定碰撞初始速度为2 m/s。为使3种碰撞情况下船舶的初始动能相同，船尾碰撞的角速度设定为0.082 3 rad/s(船尾碰撞时船体的运动方式被设为绕经过船体重心的竖直线转动)。

2.4.4 接触与边界条件

本文采用主从接触面(master-slave surface)算法模拟碰撞面之间的接触。考虑到由摩擦损失的能量不大，对摩擦计算采取简化处理，设静摩擦因数为0.10，动摩擦因数为0.05。根据《海上移动平台入级与建造规范》[16]，采用对桩腿泥面以下3 m进行铰支的方法来代替平台与海底桩土的耦合作用。

3 船撞平台的模拟计算与分析

3.1 碰撞位移

图5是在船首、船中和船尾碰撞平台情况下碰撞位移达到最大时平台的应力云图。图6为3种情况下的碰撞位移时序曲线。

从图5和6可以看出当碰撞位移达到最大值时，碰撞区域内单元的应力已经超过材料的屈服应力，材料已进入塑性变形阶段。船首碰撞的持续时间为3 s，最大碰撞位移为0.87 m；船中碰撞的持续时间为2.25 s，最大碰撞位移为1.289 m；船尾碰撞的持续时间为2.71 s，最大碰撞位移为1.13 m。通过比较可知：船首碰撞的持续时间最长，对弦管的局部破坏最严重，船首动能主要耗散在弦管的局部变形中；船中碰撞和船尾碰撞的最大位移较船首碰撞的大，其中船中碰撞的最大位移最大。这主要是因为船中碰撞和船尾碰撞使平台产生较大的整体变形，而且船中碰撞和船尾碰撞的附加质量较大，在相同初始动能(不计附加质量)的前提下，两者的实际动能(计附加质量)较大，这也是船中碰撞和船尾碰撞的最大位移较大的重要原因。

a)船首碰撞

b)船中碰撞

c)船尾碰撞图5 在船首、船中、船尾碰撞平台情况下碰撞位移最大时平台的应力云图

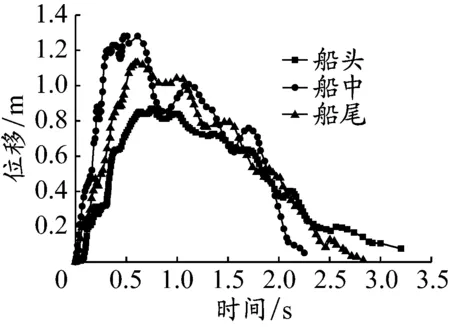
图6 船首、船中、船尾碰撞平台时的碰撞位移时序曲线

3.2 碰撞力

图7为船首、船中和船尾碰撞平台时的碰撞力时序曲线。

图7 船首、船中和船尾碰撞平台时的碰撞力时序曲线

从图7中可以看出：碰撞之初碰撞力的总体变化趋势都是增大，当碰撞位移最大时碰撞力达到峰值；碰撞力在达到峰值后并不是一直下降，而是会在下降过程中产生较小的峰值，这主要是因为船不仅碰撞了桩腿弦管而且碰撞了平台的其他构件。船首碰撞、船中碰撞和船尾碰撞的最大碰撞力分别为20.182、14.893和16.403 MN，其中船首碰撞的最大碰撞力最大，这主要是由于这3种情况中船首与平台弦管接触面的曲率变化最大，使平台桩腿的弦管受到的集中力也最大。

3.3 能量转化

由于碰撞过程中摩擦等因素损耗的能量很少，所以本文只对船的动能和平台的总吸能进行分析。图8a、8b和8c分别是船首、船中和船尾碰撞平台时船的动能和平台总吸能的时序曲线。表5为船首、船中和船尾碰撞平台时的能量统计表，其中：E0为船舶的初始动能(计附加质量)；Emax为平台总吸能的最大值；Eres为平台的塑性变形能；Pmax为平台总吸能的最大值在总能量中的比例；Pres为平台的塑性变形能在总能量中的比例。

a)船首碰撞

b)船中碰撞

c)船尾碰撞图8 船首、船中和船尾碰撞平台时船的动能和平台总吸能的时序曲线

从图8和表5可以看出：3种碰撞情况下的碰撞动能主要被平台的变形所吸收，船中碰撞时平台最大总吸能在总能量中占的比例较大，而船首碰撞时平台的塑性变形能在总能量中占的比例较大。这是因为：船首碰撞主要使平台发生较大的局部变形，碰撞区域产生的塑性变形较多；船中碰撞和船尾碰撞主要使平台发生整体变形，产生的弹性变形较多(其中船中碰撞使得平台产生的弹性变形最多)。船首碰撞使得平台结构的局部损坏最为严重，但是对于柔性较大的自升式海洋平台，如果船中碰撞或者船尾碰撞的初始碰撞动能很大(高能碰撞)，将会对平台整体造成更为严重的破坏。

表5 船首、船中和船尾碰撞平台时船的动能和平台总吸能统计

4 结 论

本文基于有限元软件ABAQUS对船首、船中和船尾与自升式海洋平台碰撞进行了数值模拟研究，通过比较得到的主要结论如下：

(1)在同一条船初始动能相同(不计附加质量)的前提下，船首碰撞持续的时间最长，碰撞力的峰值最大，对平台桩腿弦管的局部破坏最严重。船中碰撞和船尾碰撞时碰撞位移较大(其中船中碰撞时碰撞位移最大)，会使平台产生较大的整体变形。

(2)不论是船首碰撞、船中碰撞还是船尾碰撞，碰撞力的总体趋势都是先增大后减小的，船首碰撞碰时碰撞力最大，船尾碰撞时碰撞力其次，船中碰撞时碰撞力最小。

(3)撞击船的动能主要被平台桩腿的弦管变形所吸收，船中碰撞时平台最大总吸能在总能量中占的比例较大，而船首碰撞时平台的塑性变形能在总能量中占的比例比较大，说明船中碰撞使平台产生的弹性变形较多，而船首碰撞使平台产生的塑性变形较多。

参考文献：

[1] TEBBETT I E. The last five years’ experience in steel platform repairs[C]//Offshore Technology Conference, Houston, Texas, USA, 27-30 April 1987. Offshore Technology Conference, 1987: 261-268. DOI: 10.4043/5385-MS.

[2] 林一, 李陈峰, 田明琦. 船舶碰撞下自升式平台结构强度及主要撞击参数分析[J]. 哈尔滨工程大学学报, 2012, 33(9): 1067-1074.

[3] WOISIN G. The collision experiments of GKSS[J]. Nuclear Powered Ships, 1977, 8(24): 145-187.

[4] AZADI EMAMI M R. The influence of ship collision parameters on the global nonlinear dynamic response of a North-Sea jack-up platform[J]. Journal of Offshore Mechanics & Arctic Engineering, 2014, 136(4): 41-52. DOI: 10.1115/1.4028190.

[5] STORHEIM M, AMDAHL J. Design of offshore structures against accidental ship collisions[J]. Marine Structures, 2014, 37(4): 135-172.

[6] 温小飞, 卢金树, 崔振东. 船舶碰撞过程的数值模拟及试验研究[J]. 浙江海洋学院学报(自然科学版), 2011, 30(1): 71-76.

[7] VILLAVICENCIO R, LIU B, GUEDES S C. Experimental and numerical analysis of a tanker side panel laterally punched by a knife edge indenter[J]. Marine Structures, 2014, 37(4): 173-202. DOI: 10.1016/j.marstruc.2014.03.001.

[8] 包杰. 自升式海洋平台碰撞模型试验技术研究与应用[D]. 镇江: 江苏科技大学, 2016.

[9] 王自力, 顾永宁. 船舶碰撞动力学过程的数值仿真研究[J]. 爆炸与冲击, 2001, 21(1): 29-34.

[10] 陈永念, 谭家华. 数值仿真中单元密度对材料失效应变的影响[J]. 船海工程, 2007, 36(6): 1-4.

[11] HU Zhiqiang, ZHANG Dongwei, ZHAO Dongya,etal. Structural safety assessment for FLNG-LNGC system during offloading operation scenario[J]. China Ocean Engineering, 2017, 31(2): 192-201. DOI: 10.1007/s13344-017-0023-4.

[12] 王自力, 蒋志勇, 顾永宁. 船舶碰撞数值仿真的附加质量模型[J]. 爆炸与冲击, 2002, 22(4): 321-326.

[13] 元良誠三, 藤野正隆, 杉浦正憲, 等. 衝突時の等価附加質量について[J]. 日本造船学会誌, 2009, 1969(126): 141-152.

[14] POSEY C J. Protection of offshore structures against underscour[J]. Journal of the Hydraulics Division, 1971, 97(7): 1011-1016.

[15] HARGREAVES G L, PETRIE R, MOORE B B. Offshore installations: guidance on design and construction[J]. Ice Proceedings, 1978, 64(3): 513-515.

[16] 中国船级社. 海上移动式平台入级与建造规范[S]. 北京: 人民交通出版社, 2005: 3-8.