基于Memetic混合算法的桥区复杂水域船舶航路规划

杨帆， 王健宇,1b， 杨柯， 徐言民

(1. 武汉理工大学 a. 航运学院; b. 内河航运技术湖北省重点实验室, 武汉 430063;2. 安康市汉滨区交通运输局， 陕西 安康 725000)

0 引 言

近年来，自动化技术被应用到交通领域，无人机、无人艇、无人驾驶汽车等技术得到了飞速发展[1-2]。我国长江深水航道工程的实施和沿江港口的大规模建设，使交通流密度增大，局部通航条件更加复杂。目前船舶在群桥水域[3-4]航行时，仍然采用传统的手动操舵，而以往船撞桥事故主要是由人的失误引起的，因此，实现船舶在多障碍物复杂水域的自主航行，既是减少船撞桥事故的有效手段，又是急需攻克的技术难题。

船舶航路规划是实现船舶自主航行的重要前提。船舶航路规划问题属于多维非线性优化问题。如果考虑通航水域的动态障碍物，则船舶航路规划问题属于非线性时变函数优化问题[5]，这对航路规划求解算法的收敛性、时效性要求很高，传统算法难以适用。现有群智能算法具有自适应、自组织和自学习的特点，能够解决传统算法难以解决的非线性复杂问题，在航路规划方面具有很好的应用前景[6-7]，但运用该算法求解得到的多维非线性函数优化问题的解均为近似解，仍然有进一步优化的空间。

本文通过分析以长江武汉段群桥水域为典型代表的复杂水域通航特征，建立复杂水域通航环境模型，然后进一步建立复杂水域航路规划数学模型。为提高算法求解精度和求解速度，为动态环境航路规划研究奠定基础，结合遗传算法的全局搜索能力和模拟退火算法的局部搜索能力，设计了Memetic混合算法，对所建立的模型进行求解，并对规划航路进行优化处理。

1 航路规划模型

1.1 复杂水域通航环境特征简要分析

目前，学术界对于复杂水域并没有明确定义。一般来讲，复杂水域具有较为复杂的水文、交通流、通航条件、船舶状况等。本文将以群桥水域为代表的、存在近距离的多个障碍物的水域视为复杂水域。

通常情况下，桥区复杂水域的桥墩、浅点、沉船等障碍物间距小，障碍物分布无规律[8]；障碍物的挑流作用使得复杂水域的水流更加复杂；考虑安全水深因素，复杂水域内供船舶航行的水域往往被限制；复杂水域交通流复杂，船舶操纵难度大，非常容易发生碰撞事故。

1.2 桥区复杂水域通航环境建模

如果不考虑动态障碍物影响，则以桥区水域为代表的复杂水域最主要的障碍物是桥墩。本文假定研究水域障碍物为圆形。考虑障碍物的挑流作用和安全裕度，适当地扩大障碍物尺寸，在水域一定范围内随机生成大小不同的障碍物，见图1。

为使规划结果更加直观，图1中船舶被视为质点，障碍物的半径被等比例扩展，这样便可保证船舶与障碍物之间的距离仍符合要求。图1横、纵坐标中的L为船长。

包括起点和终点的所有黑点按顺序连接成的折线可表示搜索空间中的某一条路径，路径点与障碍物间的距离是判断航路危险性的主要依据。为便于在选取最优路径时进行路径长度计算，需要建立通航环境坐标系，将坐标系按如下关系进行转换：XOY为原坐标系，新坐标系为X′O′Y′，路径点在原坐标系和新坐标系中的坐标分别为(x,y)和(x′,y′)，在原坐标系中起点和终点的坐标分别为(xs,ys)和(xt,yt),θ为两个坐标系横轴的夹角。坐标转换关系见图2。

图2 坐标转换关系

路径点坐标在两个坐标系中的转化公式如下：

(1)

1.3 桥区复杂水域航路规划数学模型

船舶航行最重要的原则是安全、经济、高效，因此最优的航路规划就是找到一条从起点(xs,ys)到终点(xt,yt)的与障碍物不相交且长度最短的路径。本文先求出最短的路径，再对其进行实用化处理。按照文献[9]，航路规划数学模型为

(2)

式中：L为航路总长；J为航路跟踪代价；J1为障碍物威胁代价；J2为航路长度代价；wt表示航路上各点的威胁代价；wl表示每条边的长度代价；k为不同航路跟踪代价所占的比例，设定路径规划中障碍物威胁代价与路径长度代价同等重要，故本文k取0.5。

选取起点与终点之间线段的一部分(起始于M，终止于N)，分成10等份，在每个等分点(共9个等分点)处作MN的垂线。在每条垂线上各选择一个点，将这些点按从M到N的顺序连成一条航路LMN。当船舶沿着航路LMN航行时，威胁源(障碍物)个数为n，则总威胁代价为

(3)

为方便计算，在线段MN上取5个点(见图3)，按下式计算航路的障碍物威胁代价：

(4)

d1,k、d3,k、d5,k、d7,k、d9,k分别表示MN上的第1、3、5、7、9个等分点与第k个障碍物中心的距离。

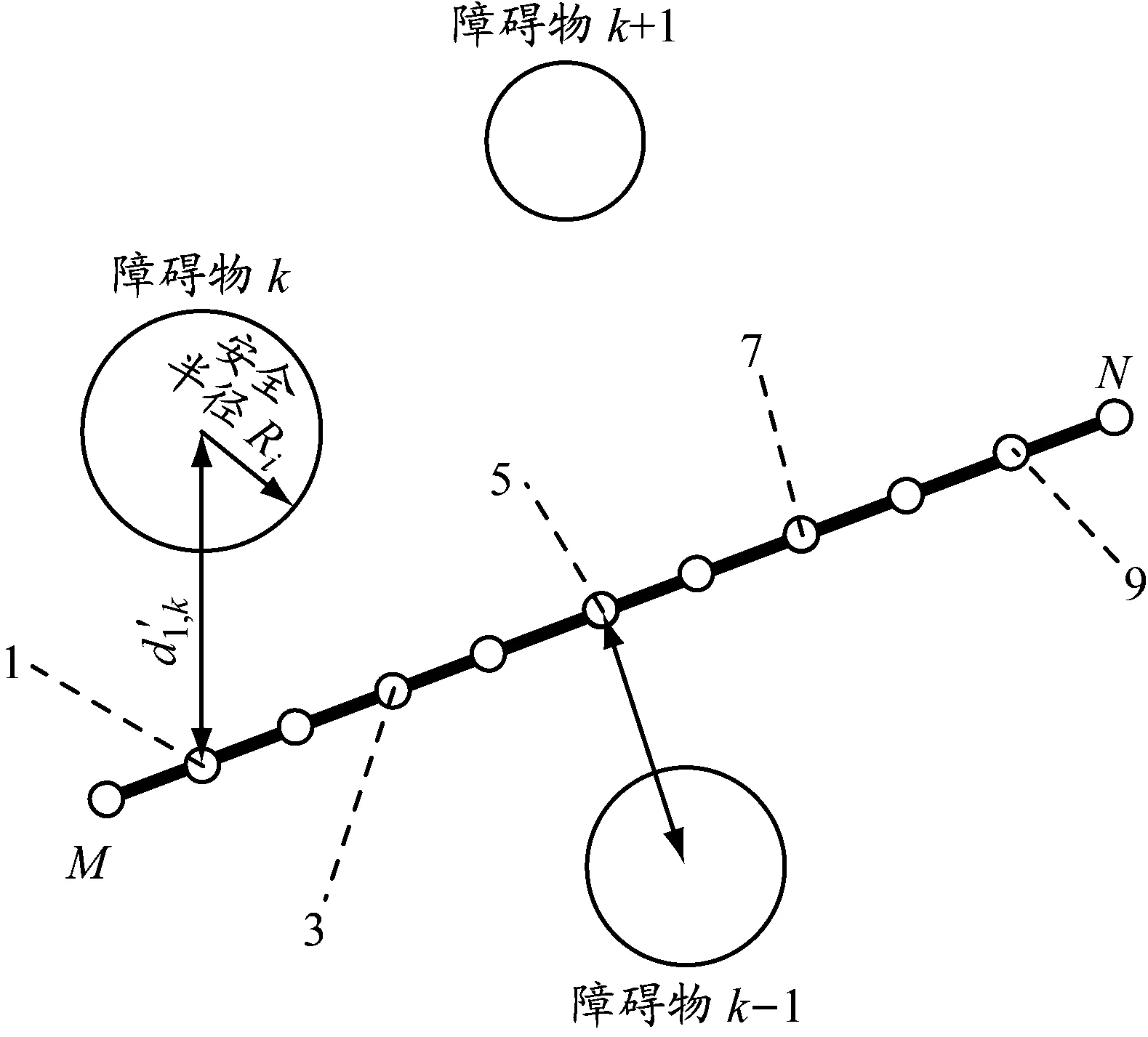
图3 障碍物威胁代价示意图

2 Memetic算法设计

2.1 Memetic算法概述

Pablo Moscato于1989年首次提出Memetic算法的概念[10]。Memetic一词由meme而来，可理解为“文化基因”，因此Memetic算法可称为文化基因算法[11]。Memetic算法最初的主要思想是在遗传算法每次迭代后对所有种群进行一次局部搜索，它实际上是一种混合算法。算法用局部启发式搜索来模拟由大量专业知识支撑的变异过程，使得遗传算法的变异得到有效的支撑，从而使算法在某些领域的搜索速度和计算精度有了极大提高。

2.2 Memetic算法设计

实际上，Memetic算法只是提供了一个算法框架，是全局搜索策略和局部搜索策略的有机结合。本文全局搜索策略采用遗传算法，局部搜索策略采用模拟退火算法。有关遗传算法和模拟退火算法的相关研究较多，这里不赘述。

通过代码设计，种群在每次更新后都会在其个体领域进行局部搜索，从而使得算法能够快速收敛于最优解。

遗传算法中参数设置的相关研究已有很多，本文选择较为常用的参数设置。降温过程的快慢会影响模拟退火算法的全局搜索能力与局部搜索能力的平衡[12]。在计算机实现中，如果降温速度慢，则会得到令人满意的解，但如果降温速度太慢，则其相较于其他简单的搜索算法不具有明显优势[13]；如果降温速度快，则该算法更容易求得局部最优解。初始温度高低也会影响模拟退火算法运行，较高的初始温度更容易求得全局最优解，但会大大增加算法复杂度，影响算法的求解时间。本文的算法更关注模拟退火算法的局部搜索能力，因此本文设置的初始温度较低，降温速度较快。

3 航路规划

根据上述算法，本文给定障碍物坐标分别为(21L，20L)，(26L，55L)，(40L，10L)，(55L，5L)，(55L，30L)，(55L，45L)，(55L，75L)，(73.3L，53.5L),(90.9L， 23.9L)。为增加航路规划难度，将航路规划的起点和终点设置在障碍物分布较为集中的连线上，起点坐标设置为(5L，5L)，终点坐标设置为(110L，70L)。分别使用遗传算法、模拟退火算法和Memetic混合算法进行航路规划。Memetic混合算法迭代次数设置为300，其中模拟退火模块内部迭代次数设置为100。求解结果见图4和5。

a)Memetic混合算法

b)遗传算法

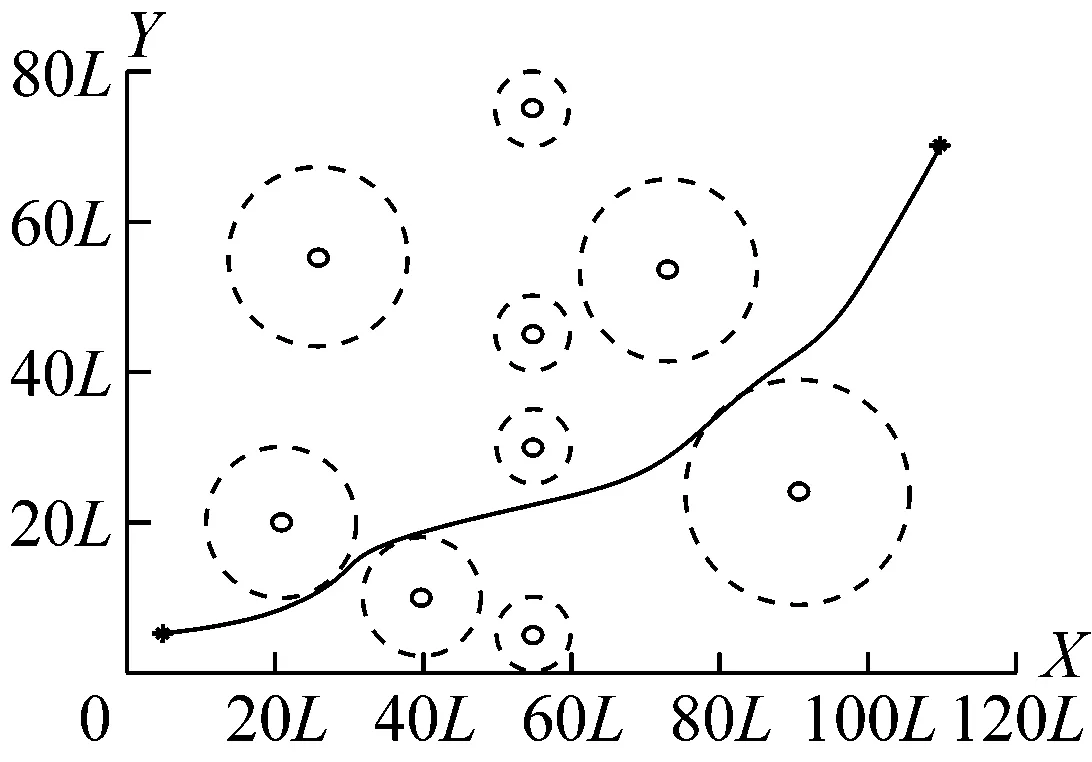
c)模拟退火算法图4 3种算法航路规划示意图

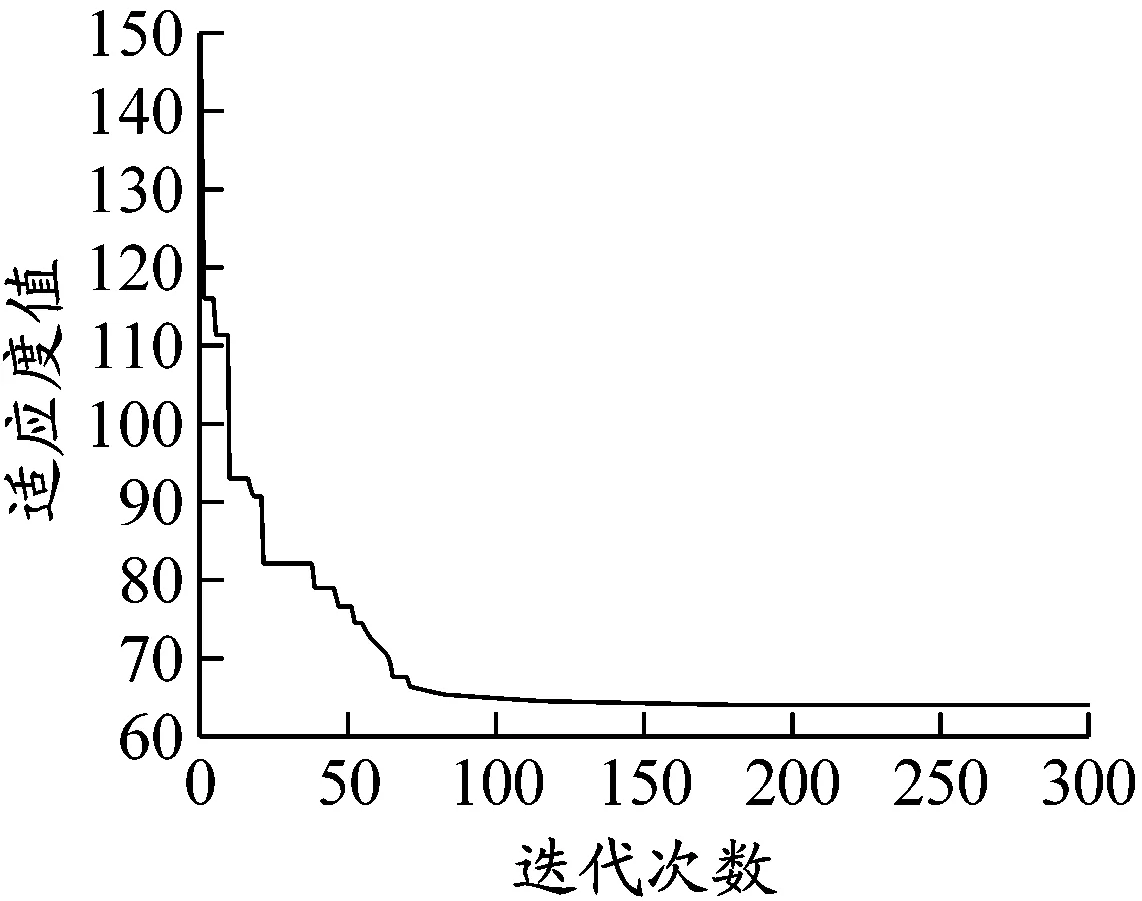
a)Memetic混合算法

b)遗传算法

c)模拟退火算法图5 3种算法迭代曲线示意图

由图5可以看出，Memetic混合算法能更快地求出最优解，算法大约在迭代次数为150时稳定收敛。

Memetic混合算法既结合了遗传算法的全局搜索能力，又在每次迭代过程中利用了模拟退火算法的局部搜索能力，使得算法收敛速度和求解精度有了极大的提高。

4 规划航路优化

针对D维优化问题，本文设计的算法能够寻找出D维最优解。对应本文所建立的规划模型，规划航路为D维向量加起始点的一组向量。为提高求解精度，常常将D取得比较大，最终求解的航路规划问题维数较多，得到的航路呈现出曲线或者有较多段线段的形态。另外，由于本文设计的算法求解的是目标函数的近似最优解，从规划结果图上可以直接看到规划航路在终点附近还存在一定的弯曲度，仍然有优化的空间。

利用所建立的模型，所选取的航路为端点(M和N)与9个节点所组成的10条线段。一种很简单的改进思想是：所求得的航路是一个近似最优解，在其附近的其他航路应该也是相对较优的。因此，可考虑在已经规划出来的10条线段中，以M点为第1个点，如果相邻两条线段的倾斜角差的绝对值小于一定的阈值，则可去掉相邻两条线段中间的点，两条线段转化为一条线段，否则这部分航路保持不变。依次进行以上操作，直到算法历经所有的11个点为止。如图6所示，假设第1个点为点k，由点k与k+1、点k+1与k+2，分别确定线段lk,k+1和lk+1,k+2。因为lk,k+1与lk+1,k+2的倾斜角差小于给定阈值，所以挖去点k+1，由新的线段l1取代原来的两条线段lk,k+1和lk+1,k+2，这样就达到了减少转向点的目的。接着对线段l1与线段lk+2,k+3的倾斜角差做上述比较，因为l1与lk+2,k+3的倾斜角差值仍小于给定阈值，所以可用新的线段l2取代l1和lk+2,k+3两条线段。

图6 航路节点优化示意图

经过试验，倾斜角差阈值的取值对最终结果有较大的影响。取阈值分别为5°、10°和15°进行试验，发现当阈值为10°时结果较为理想。取不同阈值时的优化结果见图7。

由图7b可以看出，最终的优化航路由起点、5个转向点和终点组成，一共有6个航段。

5 结 论

针对复杂水域船舶航路规划问题，建立了通航环境模型，基于遗传算法和模拟退火算法设计了Memetic混合算法，对模型进行了求解，并从航海实践角度对优化结果进行了实用化处理。实例验证表明，本文设计的算法能够快速规划出给定环境下的最优航路，并可以对航路进行进一步实用化处理，使航路规划结果更具有实际意义。本文所建立的航路规划数学模型是将船舶视为质点，并未充分考虑船舶自身动态变化，后期航路规则研究将设置船舶安全领域、气象条件等约束条件。

a)阈值为5°

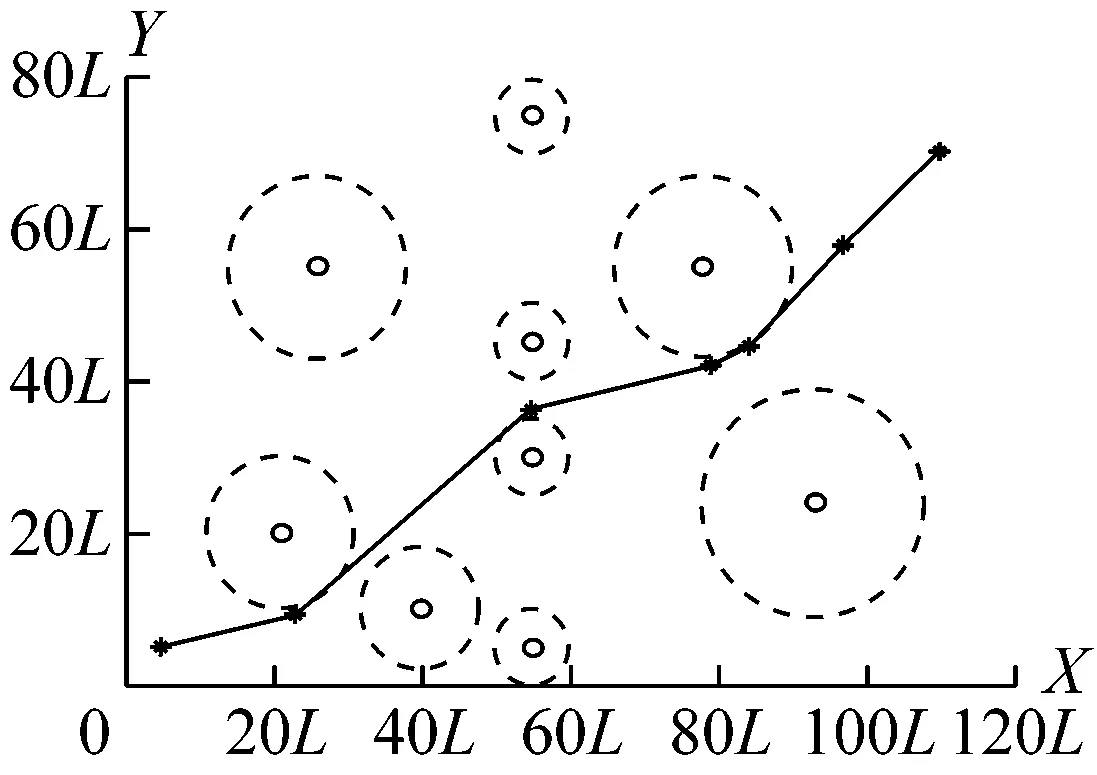
b)阈值为10°

c)阈值为15°图7 取不同阈值时的优化结果

参考文献：

[1] 杨俊超, 史越, 马海明. 一种人—自动化系统协作的无人机航迹规划方法[J]. 计算机测量与控制, 2015, 23(9): 3216-3218, 3224. DOI: 10.16526/j.cnki.11-4762/tp.2015.09.084.

[2] 吴博, 熊勇, 文元桥. 基于速度障碍原理的无人艇自动避碰算法[J]. 大连海事大学学报, 2014, 40(2): 13-16. DOI: 10.16411/j.cnki.issn1006-7736.2014.02.013.

[3] 徐言民, 杨柯, 关宏旭, 等. 基于SAPSO算法的群桥水域航路规划[J]. 中国航海, 2015, 38(3): 37-40.

[4] 徐言民, 杨柯, 关宏旭, 等. 基于混合SAPSO算法的简化群桥水域航路规划研究[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(3): 455-458. DOI: 10.3963/j.issn.2095-3844.2015.03.001.

[5] 吴剑, 张东豪. 基于卡尔曼滤波和D*算法的动态目标航路规划[J]. 电光与控制, 2014, 21(8): 50-53. DOI: 10.3969/j.issn.1671-637X.2014.08.011.

[6] 邹春明, 赵俊超, 杨柯, 等. 基于惩罚-PSO的群桥水域多约束航路规划[J]. 中国航海, 2016, 39(2): 67-70.

[7] 马文耀, 吴兆麟, 杨家轩, 等. 人工鱼群算法的避碰路径规划决策支持[J]. 中国航海, 2014, 37(3): 63-67.

[8] 徐言民, 杨柯, 关宏旭, 等. 群桥水域特征分析及建模研究[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(2): 250-253. DOI: 10.3963/j.issn.2095-3844.2015.02.005.

[9] 韩超, 王赢. 一种基于改进PSO的无人机航路规划方法[J]. 舰船电子工程, 2014, 34(4): 49-53. DOI: 10.3969/j.issn.1672-9730.2014.04.015.

[10] MOSCATO P. On evolution, search, optimization, genetic algorithms and martial arts: towards Memetic algorithms[R]. Pasadena, USA: California Institute of Technology, 1989.

[11] 刘漫丹. 文化基因算法(Memetic Algorithm)研究进展[J]. 自动化技术与应用, 2007, 26(11): 1-4, 18.

[12] 姚新, 陈国良. 模拟退火算法及其应用[J]. 计算机研究与发展, 1990(7): 1-6.

[13] 宋燕子. 基于模拟退火算法的启发式算法在VRP中的应用[D]. 武汉: 华中师范大学, 2013.