基于三节同课异构展示课的教学设计与启示*
●
(沛县第三中学,江苏 沛县 221600)
同课异构就是不同教师针对相同的教学内容依据自己对教材的理解设计各教学环节并组织教学,鉴于授课教师的个人风格、教学对象基础的差异等客观因素的影响,教学效果可能会千差万别,因此,教学设计的科学性会直接影响授课的效果.近期笔者所在县教研室组织了一次同课异构活动,旨在为与会教师提供一个学习、对比、交流的平台,以促进一线教师思考如何对教学精准把握,从而提升教师的教学科研水平,提高教学质量.笔者观摩了3位授课教师精彩的课堂,会后对比他们对各教学环节的处理,结合学生的表现并认真思考形成了对教学设计的一些看法,现整理成文与读者交流.
1 基本情况
1.1 授课教师与学生
授课的3位教师来自3所不同的学校,下文简称“师1、师2、师3”,他们的基本素质较好,且具有较强的课堂掌控能力.学生则来自一所层次较好的初级中学七年级的3个班级,他们在自主学习、合作交流等方面养成了较好的习惯.
1.2 教材分析
教学内容为新苏科版《数学(七年级下册)》第9.3节“多项式乘多项式”,前面学习了“单项式乘单项式”与“单项式乘多项式”,后面是“两组特殊的多项式乘多项式”(即完全平方公式与平方差公式),本节内容起到承上启下的作用.
教学目标1)知道利用乘法分配律将多项式乘多项式的运算转化为单项式与多项式的乘法运算;2)能熟练进行多项式与多项式的乘法运算;3)经历探索多项式与多项式乘法运算法则的生成过程,培养有条理的语言表达能力.
教学重点多项式与多项式乘法运算的法则.
教学难点探索多项式与多项式乘法运算法则的生成过程与法则的应用.
2 教学过程
2.1 情境创设与知识生成
片段1
师1:请同学们认真思考以下4个小题:
1) (-xy)·(-2x2y);
3) -m2n·(m-n);
(教师展示课件的同时,学生在导学案上完成以上4个小题,并选取4名学生进行板演,时间共3分钟,集中点评后教师提出问题引入新课.)
师1:请同学们观察下图(图1),回答问题.
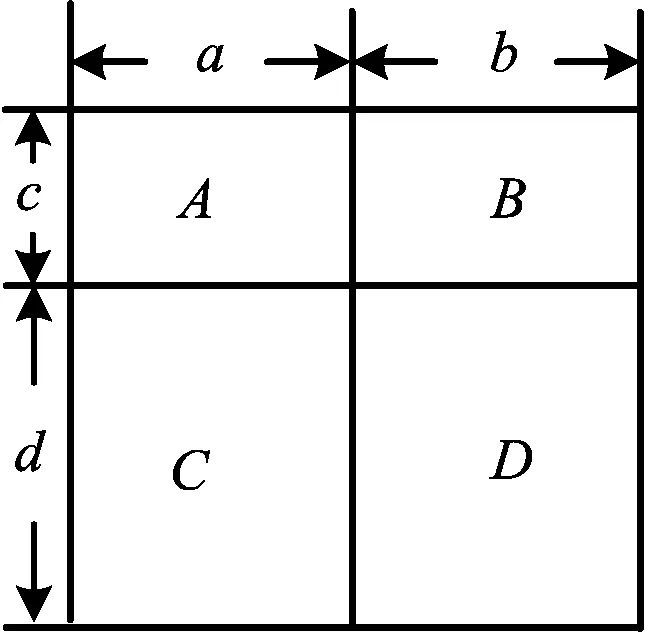
图1
1)大长方形的长为______,宽为______.
2)图1中小长方形A,B,C,D的面积分别为______,______,______,______;它们的和为______.
3)由第1)和第2)小题可得出等式______.
(小组合作交流,时间3分钟.)
片段2
师2:同学们,我们来看几个问题并解决它们:
1) (-2a2c)·(-3bc);
2) -6a·(a-3b);
3)m(c+d).
(学生板演,教师集中点评.)
师2:问题是数学的心脏,同学们认同老师的观点吗?请举手示意.好的,我们将第3)小题中的m换为a+b后题目变成了(a+b)·(c+d),问题的结果又如何呢?以前我们学过吗?
生(众):没有.
师2:要想解决这个问题,请同学们先将学案上的图形沿线剪一剪、想一想、拼一拼,并观察大长方形的面积有几种表示方法.
(学生通过小组合作,通过动手、实验、交流等环节课堂气氛异常活跃,时间10分钟.)
片段3
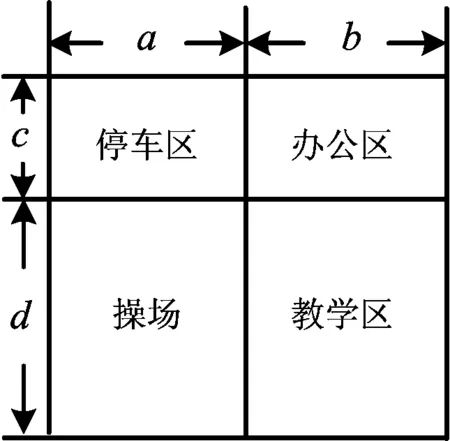
图2
师3:同学们,走进你们美丽的校园后发现校园的平面图(图2),你能结合图形中的尺寸从不同的角度求出大长方形的面积吗?有几种方法?用式子表示你的发现.
(学生带着自己学校的平面图,自豪、认真地观察图形,小组交流时间5分钟.)
点评3位教师对教材的理解出现了比较鲜明的差异,师1遵循教材,层层递进,先是设计了“单项式乘单项式”与“单项式乘多项式”的4个小题为本节课的新授内容作铺垫,接着直接给出图形并提出大长方形面积的不同求法,问题具有很强的针对性,学生只要从数与形的角度思考即可,且不难得出答案.而师2开始采取了与师1相同的方法,选取简单的题目开场,其中第3)小题来源于课本,问题难度不大,但教师提出“将m换成a+b”完全激发了学生的学习积极性与求知欲,同时教师结合学生已有的基本活动经验通过动手剪纸、观察、拼图将课堂带入一个小高潮,学生沿不同的线裁剪得到不同的长方形.师3直奔主题欣赏授课学校的平面图,结合图形也具有耳目一新的感觉,在提高学生学习兴趣方面具有不可忽视的作用.但HPM教学模式主张借鉴历史、重演历史和重构历史通过再创造的方式使学生获得数学知识,提升数学素养[1],它的应用有时需要借助已有的认知,但师3直奔主题略显突兀,缺少了铺垫环节.而从不同的角度研究大长方形的面积,3位教师的设计构思相差不大,均是由学生自主总结归纳出多项式乘多项式的法则,从而完成知识的生成.数学教学的基本要求就是通过具体的问题串进行适时引导,层层递进,螺旋式上升得出一个感性认识,再通过归纳、类比等手段概括出基本概念与数学思维,进而对具体问题实施操作,最终获得对问题本质的认识.
2.2 数学应用
作为教学中的重要一环,例题具有很强的示范性,形成“多项式乘多项式”的法则后如何运用公式解决问题摆在学生面前,3位教师均选取课本上的例题作为讲解重点,但3位教师处理的方法略有不同,师1与师3均是自己通过板演示范一道题,另一道题则交给学生通过交流后板演,而师2则是只讲解题思路,其他全部交给学生完成.
例题是新知所涵盖的数学方法、数学思想应用的集中体现.对比3位教师的做法,师1与师3的做法是先示范,后学生依葫芦画瓢,相对错误率较低,而师2只讲思路不写解题过程后放手学生,导致后续做题不规范,经过教师的不断引导有所改进但难免错误不断,因为新知应用还没有成为学生已经掌握的内容.
2.3 习题演练
片段4
师1:我们学习了多项式乘多项式的法则,请同学们完成一组判断题:
1) (a+b)(c+d)=ac+ad+bc;
2) (a-b)(c+d)=ac-bd+bc-ad;
3) (a+b)(a-b)=a2-ab+ab-b2.
(3道判断题采取口答的方式完成,旨在巩固法则中经常出现的错误.)
师1:请同学们再来看一组计算题:
1) (a+4)(a+3);
2) (x+2)(x-3);
3) (x-2)(x-3).
(学生交流后板演,时间5分钟.)
师1:通过这一组计算题,同学们有什么收获?
(学生讨论,师1引导学生归纳、总结规律:(x+a)(x+b)=x2+(a+b)x+ab.)
片段5
师2:同学们,累不累?
生(众):累!
师2:那好,我们休息一下做一个游戏.
生(众):什么游戏?
师2:我们来做一个“答题接龙”的游戏.
(学生又从疲惫中兴奋起来,师2展示课件上的幻灯片.)
师2:生1你选择几号卡片?
生1:我选1号卡片.
师2:哇,运气真好,请计算(x+1)(x+2),好简单!……
(教师不断激励学生勇于探索,学生抢答不断.)
点评习题演练是巩固新知的重要手段,通过学生交流、操作、对比、反馈等可以加深对新授知识的进一步理解.教师选取层次合理的题目可以让学生在发现问题、分析问题、解决问题的过程中自我纠正,掌握易错点.但习题演练的实际效果可能受学生疲劳感等客观因素的影响,如何恰当地选择教学设计至关重要,师1主要采取合作交流、板演、多媒体展示、互批等方式,最后还引领学生归纳出一个“副产品”:(x+a)(x+b)=x2+(a+b)x+ab,并应用结论解决与之相关的题目.但在总结结论等环节上遇到了困难,原因是多方面的,如结论的生成难度高于学生认知新事物的能力,同时偏离了本节课教学的重点,盲目扩大课堂容量也会给初中学生带来不小的难度;七年级学生的课堂专注力集中在前20~25分钟,而师2显然注意了这一点,他采取了游戏的方式,学生对于谜底的探求产生了好奇心,总想知道每张卡片下面到底是什么题目,是简单的还是复杂的,从而激发了学生参与活动的积极性.该设计避免了随课堂不断深入给学生带来的疲倦,还将课堂带入另一种境界,且师2准备了8张卡片共8道题目可随时间限制合理取舍,师1和师3则是选取传统的教学手段,结合学生活动的参与也取得不错的教学效果.教学是一门艺术,作为一线教师要思考如何在短暂的45分钟课堂巧妙设计,从而不断激发学生的学习兴趣,将学习效率提升一个层次.
2.4 当堂检测与小结思考
当堂检测是检验学生学习效果的必要手段.师1引导学生归纳(x+a)(x+b)=x2+(a+b)x+ab,并应用它来解题.师2在知识生成环节综合了数学实验,在巩固练习环节采取了答题接龙的数学游戏导致时间不是那么充裕,只能将当堂检测放到课后让学生自主完成.有人说课堂必须有课堂检测否则就有缺陷,但南京师范大学附属中学的特级教师马明老师说过:教学中完美的课堂很多是不完整的课堂,意思是只要将思维活动凸显出来即使缺少某些环节也是一节好课.
在小结与思考环节,3位教师均采取了由学生自主总结本节课所学知识的教学设计,学生自始至终参与活动,这与江苏省徐州市推行的“学进去、讲出来”的课改思路一致.
3 教学启示
3.1 充分体现学生学习的主体性
3位教师均采取了让大多数学生参与活动的教学策略,换言之就是将时间还给学生,让学生成为课堂的“主演”,而教师则扮演“导演”的角色,这与学生接受新知的一般规律相符.如何将时间还给学生?笔者认为应注重以下两点:一方面在教师给出问题后,可通过小组合作交流等让每个学生都参与到知识的生成过程中来,在表达自己的观点与见解时教师应少讲而是要倾听学生的声音;在例题讲解与课堂巩固等环节教师应鼓励学生多练而教师只需精评,在大量练习后总结出结论与课堂小结也应让学生感知总结而非教师越俎代庖.另一方面学生成为课堂的主人并非教师放纵他们“无法无天”,教师扮演引路人的角色并非形如路人,教师应该适时抛出问题,以问引思、以问促疑、以问导学.师2则开门见山询问学生是否同意“问题是数学学习的心脏”的观点,可见问题是教师掌控课堂节奏、不偏离教学目标方向的重要手段之一.
3.2 突出数学实验的重要性
数学实验不同于物理、化学、生物等实验,它的操作灵活多样,即可借鉴多媒体带来的数字化统计与图像动态演示上的便利,有时又可不依赖于实验室而仅仅借助对实物的操作,教具可简可繁.本节课师2借助导学案上印制的可裁剪与拼接的图1,使学生的活动是“做数学”而非“听数学”,这里的设计明显是一个亮点,师2的答题接龙也巧妙地利用现代多媒体将教学形象直观生动地展示出来.
但在实际教学中,很多课堂对数学实验的开发利用不是特别充分,其原因可能是多方面的,如课堂容量制约教学环节的时间,学生实验时间长了导致不能完成既定的教学任务;又如学生活动中穿插实验内容比传统的方法麻烦,不如直接以问题引领思考更加简洁;再如很多教师认为加大习题演练的成分而压缩数学实验的比例更能促进学生掌握知识方法等等.但数学实验给学生带来的是亲身经历的实实在在的生动的数学而非枯燥繁琐的图形与文字,这是传统与现代两种教学理念的碰撞,从师2的剪纸游戏可以看出实验能紧紧吸引学生的注意力,在不同的剪纸方法活动中得出不同的公式,对提高学生思维的深刻性、灵活性、广阔性具有不可替代的作用.
3.3 注重数学思想与数学方法的渗透
掌握解决问题的方法比知识本身更重要,而且提升解决问题的能力不是一蹴而就的,它需要教师经常进行有针对性的训练与点拨,也需要学生在活动中不断积累.数学思想方法就是发现问题、分析问题、解决问题的钥匙.
3位教师的教学设计均关注了诸多的数学思想方法,如他们均采取数形结合的思想来引入新课,结合图形整体来看长方形的面积是多少、每一个小长方形的面积是多少、它们的和是多少……通过以上问题的设置将图形和数、式联系起来,在活动中实现教学目标的达成,也有学生从不同的角度认为图1是两个长方形构成的,另辟蹊径得出公式(a+b)(c+d)=a(c+d)+b(c+d),这里就是初中数学教学中整体思想的体现,进而学生体会了多项式乘以多项式也可转化为单项式乘以多项式,这种转化与化归的思想潜移默化地开拓着学生的思维.
4 结束语
授课的3位教师身上均体现出扎实的基本功与严谨的教学态度,他们多维的角度、迥异的风格、不同的策略在活动中碰撞、升华,值得与会的每一位教师学习.好课的评判没有严格的标准,以上只是笔者一些粗浅的看法,不当之处敬请批评指正.
参 考 文 献
[1] 郭宗雨.HPM教学模式案例[J].中学数学教学参考,2014(8):6-9.

