双机并车齿轮箱中齿轮啮合振动仿真
程治斌, 周瑞平
(武汉理工大学 能源与动力工程学院, 湖北 武汉 430063)
0 引 言
随着全球经济的飞速发展,船舶在各个领域都有极大的使用价值,无论是民用、商用还是军用,船舶的载重量均越来越大,对船舶航行速度的要求也越来越高,与此同时,对船舶动力与能效的要求也相应提高。很多时候,常规单个柴油机推进的动力系统已无法满足厂家或使用者对船舶性能的要求,在这种情况下,船用柴油机的并车运行越来越多。
双机并车的推进体系相较于单机单桨的推进系统有以下特点:
(1) 船舶的航速范围更大,低速航行时可以只启用1台柴油机,高速航行时再将2台柴油机同时开启。
(2) 双机并车是多机操作系统,航行可靠性高,当1台推进柴油机发生故障时,可以启用另1台推进。
(3) 由于离合器的存在,双机并车系统更便于维修和开展系泊试验。
(4) 控制操作相较于一般的传统单机单桨推进系统更为复杂。
(5) 需增加齿轮箱,且齿轮箱传动结构比一般单机齿轮箱复杂。
正是基于这些双机并车动力系统的特点,双机并车的齿轮箱在2台柴油机都并入运行时,会受到更为复杂的激励,故而齿轮系统在自身啮合时产生的啮合振动也更加复杂,仅通过齿轮副定义传动结构使用齿轮模块自行运算仿真得到的结果与实际情况相比可能会有较大误差,因此如何准确地定义齿轮工作啮合时的激振力进而得出对齿轮系统啮合时准确的运动学分析具有重要意义。本文以武汉理工大学动力装置实验室的双机并车试验台架为研究对象,采用PRO/E参数化命令流的建模方法,对台架非标准斜齿轮系统进行合理建模,以Hertz碰撞理论为基础,定义齿轮工作所产生的激振力及相关参数,对双机并车齿轮箱齿轮啮合振动进行仿真研究,经实例验算,结果可靠。
1 非标准斜齿轮的参数化建模
基于对研究对象与内容的整体把握,双机并车齿轮啮合振动仿真流程如图1所示。

图1 仿真流程图
在双机并车系统的试验台架设计时,考虑到2台柴油机并车工作的特性与台架上需要进行的相关试验需求,该并车系统内的斜齿轮没有采用标准齿轮参数进行加工,而是采用通过自身试验需求与实际情况向厂家提供参数而加工的非标准斜齿轮,如今主流CAD三维建模软件中设有齿轮模块,可直接调用自动生成齿轮模型,但仅限于标准参数的齿轮系列。为保证并车齿轮系统振动响应仿真的真实性与齿轮系统模型的准确性,同时考虑到Adams自身建模的局限性,故采用三维软件PRO/E对并车齿轮系统中的非标准斜齿轮进行参数化建模。
将台架图纸中的非标准斜齿轮参数输入到建模软件中,如图2所示,之后在PRO/E软件的关系选项中,通过设置ha=(hax+x)×mn、hf=(hax+cx-x)×mn、d=mn×z/cosβ、da=d+2×ha、db=d×cosα、df=d-2×hf来约束齿轮的几何关系,其中:z为齿轮齿数;mn为模数;α为压力角;β为螺旋角;ha为齿顶高;hf为齿根高;x为变位系数;d为齿轮基圆直径;da为齿顶圆直径;db为基圆直径;df为齿根圆直径。选择笛卡尔坐标系,设置该坐标系下的渐开线方程:r=db/2、x=r×cosθ+r×sinθ×θ×π/180、y=r×sinθ-r×cosθ×θ×π/180、θ=t×45、z=0来约束齿轮渐开线,最终得到1对非标准的斜齿轮模型,如图3和图4所示,并车系统的整体齿轮模型装配如图5所示。
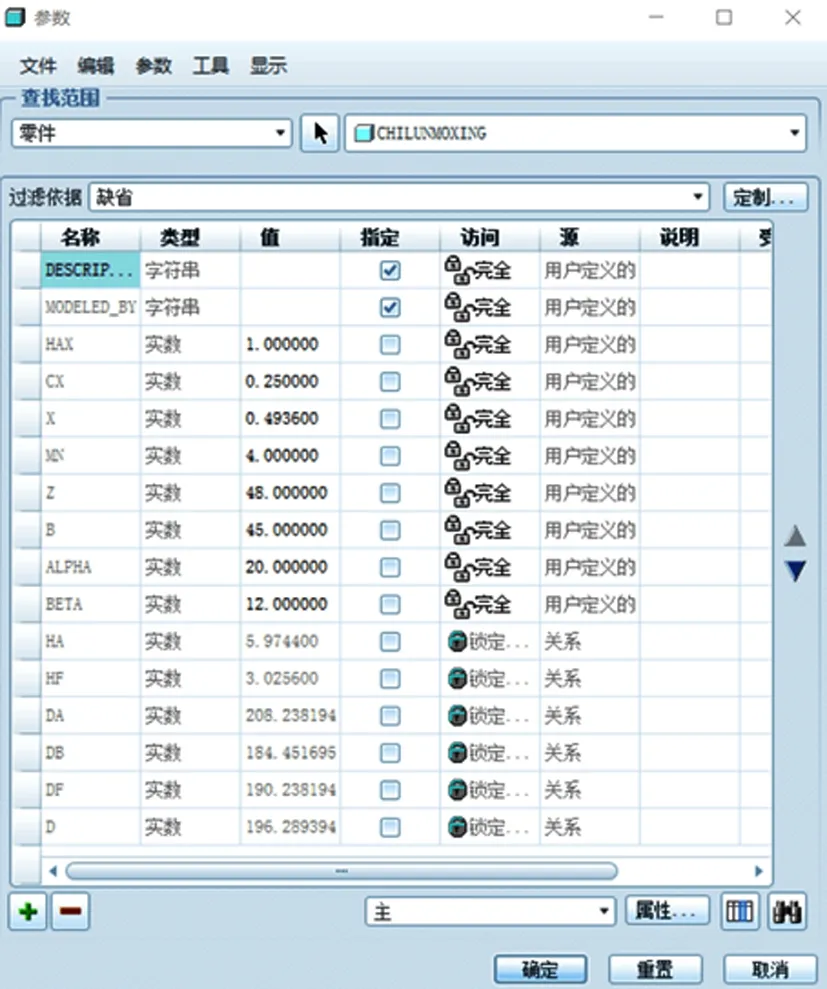
图2 参数设置

图3 齿轮1

图4 齿轮2

图5 齿轮系统装配图
2 基于碰撞理论的激振力分析
齿轮在运动过程中发生碰撞进而产生激振力,利用Hertz碰撞理论,可将1对齿轮简化为2个变曲率半径的圆柱体碰撞,在模型计算中设置齿轮的激励力。
首先建立1对旋转体的空间坐标系,如图6所示。定义a为这1对旋转体接触区的有效尺寸,R为相对曲率半径,R1和R2表示每个物体的有效半径。在产生变形之前,这1对旋转体表面上对应点S1(x,y,z1)和S2(x,y,z2)之间的间隙h可通过Hertz理论对接触区的几何假设得出:

图6 旋转体示例
在相对运动的过程中,两旋转体点T1与T2各自向原点平行于z轴移动,移动的距离分别为δ1与δ2。若这1对旋转体未发生变形,那么轮廓将会如图6中虚线所示重叠。每个旋转体由于产生的接触压力发生了平行于O2的位移,若变形之后的S1与S2重合,则1对旋转体在z方向上的相对位移有如下关系:
Uz1+Uz2=δ1+δ2-(x2+y2)/2R
=δ-(1/2R)r2
(2)
同时,作用于2个互相接触的无摩擦旋转体之间应力p与压力p0的关系可通过Hertz理论得出:
p=p0{1-(r/a)2}1/2
(3)
法相位移为
Uz=πp0(1-γ2)(2a2-r2)/4Ea
(4)

将Uz1与Uz2方程表达式代入式(4)中:
πp0(2a2-r2)/4aE*=δ-(1/2R)r2
(5)
由此可得接触圆半径为
a=πRp0/E*
(6)
两旋转体的总载荷与压力关系为
P=2πp0a2/3
(7)
由式(7)可得法向力P与变形δ的关系为
P=Kδ1.5
(8)
式(8)中:K是与物体的材料与形状相关的特征值。
本文的研究对象是齿轮传动系统,而齿轮在工作过程中啮合点是变化的,且渐开线上不同点之间的曲率半径也不相同,所以各啮合点曲率半径不等。对于斜齿轮,单就每个运动中的端面而言,都可等同于直齿轮的端面。因此有
(9)

(10)
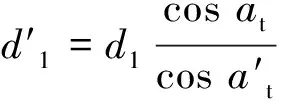
(11)
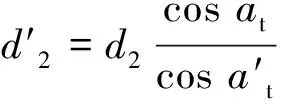
(12)
ρt2=uρt1
(13)

由上式可得
(14)
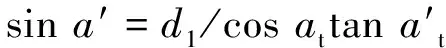
(15)

(16)
式(14)~式(16)中:d1为齿轮分度圆直径;βb为齿轮基圆的螺旋角,βb=arctan (tanβcosat);β为齿轮螺旋角。
斜齿轮的接触刚度系数K为
(17)
3 齿轮啮合振动仿真计算
将之前在Pro/E软件中建立的并车系统齿轮传动模型导入Adams后,结合之前通过Hertz碰撞理论得到的齿轮参数计算方法,同时根据齿轮系统自身的运动规律,设置好齿轮与传动轴之间的约束,定义齿轮轴自身的转动副,将每个部件定义为钢材,计算其质量、转动惯量、惯性矩、惯性积。
基于前文中的接触力理论,定义Adams中的齿轮啮合接触力。采用Impact函数计算齿轮啮合的接触力为
(18)
根据该试验台架的模型可得各级齿轮刚度系数为6.22×105N/mm3/2,另外,通过查阅材料碰撞参数,得出碰撞指数e取1.5;阻尼系数C取50 N·s/mm;变形距离取0.1 mm。考虑碰撞时的摩擦作用,2对齿轮均按润滑处理,取动摩擦系数为0.05,静摩擦系数为0.08,静摩擦速度为0.1 mm/s,动摩擦速度为10 mm/s,选择GSTIFF作为动力学积分器。
此处需要注意的是,由于在双机并车的运行初期与柴油机停止工作前期,并车系统自身的齿轮啮合振动都是受到突变的激励产生,此时的仿真结果与并车系统真正运转时齿轮传动系产生的啮合振动不符,因此将上述参数设置完毕之后,取1个平稳的运转周期之内的工作情况,在双机并车试验台架的额定转速工况下(1 200 r/min),对齿轮的啮合振动进行仿真,得到各个接触对在啮合时的冲击力仿真结果,如图7~图12所示。
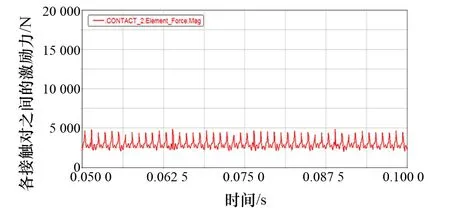
图7 接触对冲击力时域图1
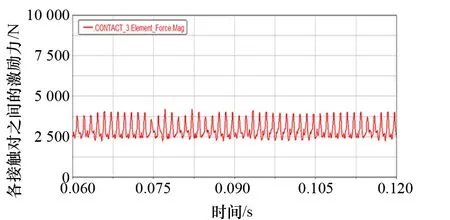
图8 接触对冲击力时域图2
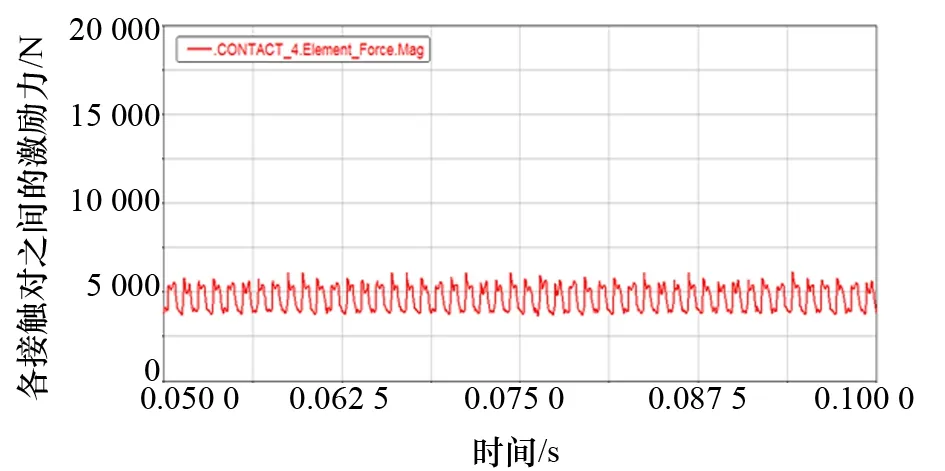
图9 接触对冲击力时域图3

图10 接触对冲击力时域图4

图11 接触对冲击力时域图5

图12 接触对冲击力时域图6
通过上述对齿轮啮合时的冲击力仿真时域图进行分析,不难得到,各个齿轮接触对在齿轮啮合运动时的冲击力都呈有规律的波动状态,这与齿轮实际运动过程中的物理状态与规律吻合,最大的接触对冲击力在时域图5中,这是由于第5对齿轮接触对在实际工作过程中不仅受到后方柴油机,还受到上方电机的双重负载,在仿真过程中对该接触对的激励设置较之于其他接触对更大,因此得到最大冲击力的仿真结果。
为验证并车系统中齿轮传动系统的齿轮啮合运动仿真结果的正确性,基于Hertz碰撞理论,定义激振力参数设置方法的准确性,提取其中1个接触对的仿真计算结果进行3个方向(即齿轮切向、径向和轴向)的分解如图13所示,利用经典机械公式计算齿轮力,与该分解后的结果进行对比。

图13 冲击力分解图
设置负载转矩T为50 000 N·mm,进行计算和验证。
齿轮切向力Ft为
(19)
齿轮径向力Fr为
(20)
齿轮轴向力Fx为
Fx=Fttanβ
(21)
计算后的结果:齿轮切向力Ft=509 N;齿轮径向力Fr=185.3 N;齿轮轴向力Fx=108.2 N。
通过经典机械公式计算所得的齿轮力与Adams软件仿真得到的齿轮冲击力对比,可得到如表1所示的对比结果。

表1 机械公式计算所得的齿轮力与Adams软件仿真得到的齿轮冲击力结果对比
通过表1的对比可知:运用Adams软件仿真的并车系统中齿轮系统的齿轮啮合力与理论计算结果误差在可接受范围内,说明基于Hertz碰撞理论的齿轮碰撞参数设置方法具有可行性,通过该方法仿真得到的齿轮啮合力仿真结果具有正确性。
[][]
4 结 论
本文以双机并车动力系统试验台架为基础,在PRO/E软件中合理创建了非标准斜齿轮与传动系统的三维模型,以Hertz碰撞理论为依据,在Adams中定义每个齿轮啮合接触对的激振力,进而对整体双机并车动力系统工作所产生齿轮啮合振动进行仿真,经过验算,结果可靠。该方法弥补了Adams齿轮副仿真模块在仿真分析齿轮啮合力时的不足,通过对实例的仿真计算,验证了方法的合理性,为工程中复杂齿轮传动机构的啮合力计算提供参考与理论依据。
[ 1 ] 唐增宝,周建荣. 直齿圆柱齿轮传动系统的振动分析[J].机械工程学报, 1992,28(4): 86-93.
[ 2 ] 李润方,陶泽光,林腾蛟. 齿轮啮合内部动态激励数值根据[J].机械传动,2001,25(2):1-3.
[ 3 ] 李润方,林腾蛟,陶泽光. 齿轮系统耦合振动响应的预估[J]. 机械设计与研究,2003,19(2):27-29.
[ 4 ] 王建军,李润芳. 齿轮系统间隙非线性振动研究综述[J].非线性动力学学报,1995,92(3):214-221.
[ 5 ] 金杨福,胡晓冬. 基于Pro/E的直齿圆柱齿轮参数化设计[J]. 轻工机械,2006,24(4):79-81.
[ 6 ] 王龙宝. 齿轮刚度计算及其有限元分析[D]. 镇江:江苏大学,2007.
[ 7 ] 谢海东,周照耀,夏伟. 斜齿轮精确建模及有限元模态分析[J].现代制造工程,2004(11):55-56.
[ 8 ] JIANG H,HE Z,DUAN C,et al. Gearbox fault diagnosis using adaptive redundant lifting scheme[J]. Mechanical Systems & Signal Processing, 2006,20(8):1992-2006.
[ 9 ] MAYEUX F, RIGAUD E, PERRETLIAUDET J. Dispersion of critical rotational speeds of gearbox:effect of bearings stiffnesses[J]. Mecanique & Industries, 2003.
[10] 徐向阳.柔性销轴式风电齿轮箱动力学研究[D].重庆:重庆大学,2012.

