曲面快速展开之三角线法
姚 方, 王雪林, 李 迅
(上海江南长兴造船有限责任公司, 上海 201913)
0 引 言
空间形体的表面在平面上摊平,这个过程称为展开。构成形体的表面可以分为2类:球面、圆环面等表面不能摊平的不可展曲面;平面、柱面、锥面等表面可以摊平的可展曲面。对于不可展曲面,常将它们分割成若干部分,把每个部分看作为可展直纹曲面并将其近似地展开。以下可展直纹曲面简称为曲面。
在船舶生产设计中经常会遇到需要得到曲面展开图的情况,比如锚台、侧推、曲面开孔等放样下料时,在工装设计中也会遇到求曲面零件展开图的情况,虽然在Tribon系统中可对曲面板架自动展开,但需要经过一系列的工程配置和曲面建模工作,繁琐且不适合于工装设计等非船工程。此时若有一种轻量级的插件直接在AutoCAD中运行能得到所需的结果,无疑会给设计工作带来极大方便。虽然很多大型成熟软件如TRIBON、CATIA、UG、PROE、SolidWorks、Rhino等均拥有曲面展开功能,但关于曲面展开的公开算法却并不多见。Tribon M3中运用的NURBS曲面对于轻量级的曲面展开算法而言并不适用,而一些软件则不能很好地根据已有详细设计图纸中的曲线建模,只能近似建模,使得建模精度不易控制。若直接在AutoCAD中使用三角线法手动放样展开曲面,也可得到较为精确的展开图,但求每条直线实长的过程需要大量的重复计算和绘图操作,枯燥耗时且容易出错。为此,根据放样展开基本原理对AutoCAD软件进行二次开发,实现自动批量求直线实长的功能,使用三角线法编程展开曲面而不借用其他图形库使得算法轻量简单,展开精度可控并可达到生产设计要求,可以帮助设计人员较为快速地绘制曲面展开图。
1 三角线法概念
几乎所有的曲面展开方法都是以近似的方式展开,采用三角线法,将曲面板分成近似于平面并且互相联系的三角面(3边组合成稳定的三角形),再把所有的三角面摊平组合后展开得到所需要下料的零件。图1为待展开曲面图,将曲面板划分成近似于平面并且相互联系的三角面,得到图2所示图形,然后将空间方向的一个三角面旋转角度放置到一个平面上,从而得出这个三角形真实形状尺寸,而后逐个将三角形放置在这个平面上就可以得到曲面的近似展开图。三角面划分越多,所展开的零件越精细,但工作量也显著增大,因此,编写程序将面板划分为非常细小的三角面,通过计算机高速运算后得到展开零件。
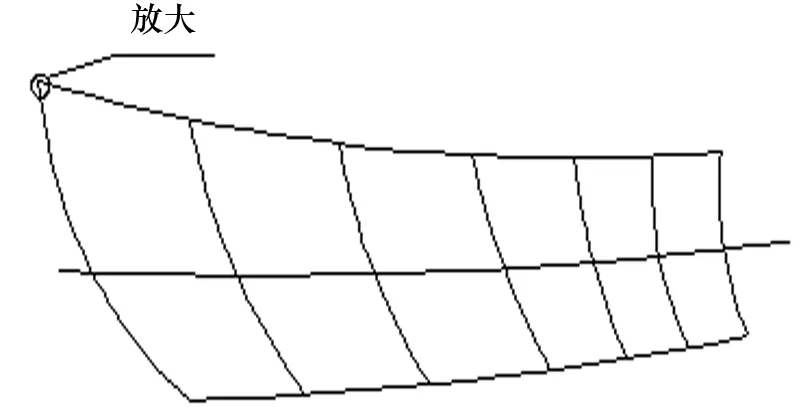
图1 待展开曲面

图2 三角面划分
2 展开基本原理
在几何画法中,可以通过1条直线段(以下将直线段简称为直线)的主视图和俯视图得到直线的实长。主视图中直线的高与俯视图直线作为1个直角三角形的2条直角边,该直角三角形的斜边即原直线的实长。
如图3所示,同一组配对直线内line 1的首尾端点坐标分别为(x1,yZ1)和(x2,yZ2),line 1'的首尾端点坐标分别为(x1,yF1)和(x2,yF2)。根据几何画法中求直线实长的原理:
line 1的高为
a=|yZ1-yZ2|
line 1的长度为
所以直线实长为
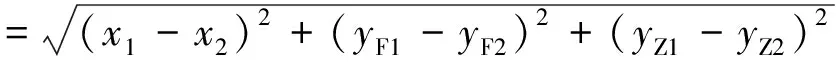
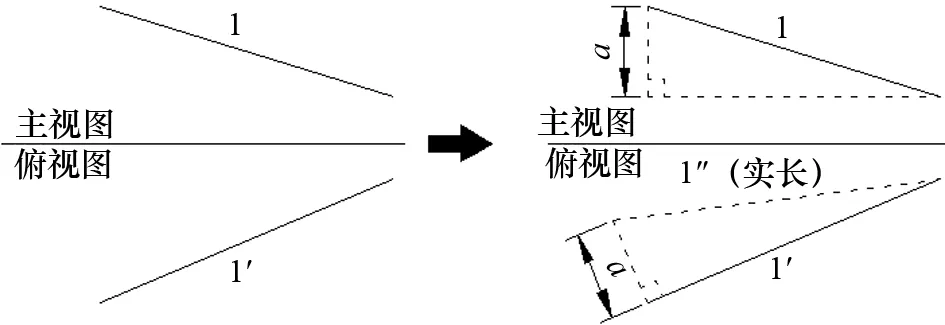
图3 求直线实长方法
根据此方法可通过一个三角形的主视图和俯视图求出该三角形三条边的实长,即空间三角形摊平在平面上的形状。如图4所示,选这3条边任意1条作为展开基准(即基准边),基准边的端点作为画圆弧的圆心点,再以其他2条边的实长作为半径画弧求出交点后连接交点和基准边端点,得到的图形就是三角面的实际外形尺寸。

图4 求三角形实形方法
如图5所示,将曲面沿直母线划分为若干个三角形,三角形顶点位于曲面顶点或边缘。然后求出所有三角形实形,并在平面上依序组合,就得到了曲面的展开图。三角形划分的越多,所得到的展开图就越精确。
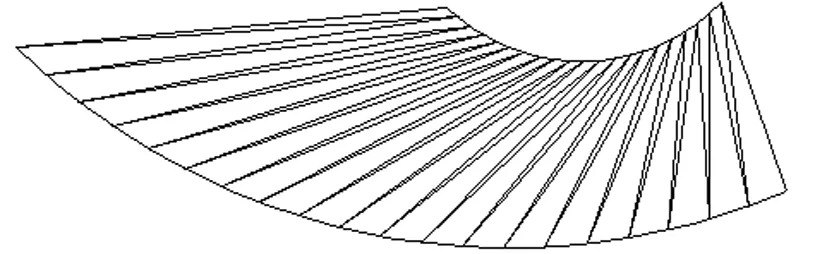
图5 沿直母线划分三角形
3 原始图形要求
如图6所示,首先要有曲面的主视图和俯视图,并且分界明显,如果为其他视图关系则旋转成主视图和俯视图。根据直母线划分三角形,三角形要求上下对应,所有直线颜色相同。
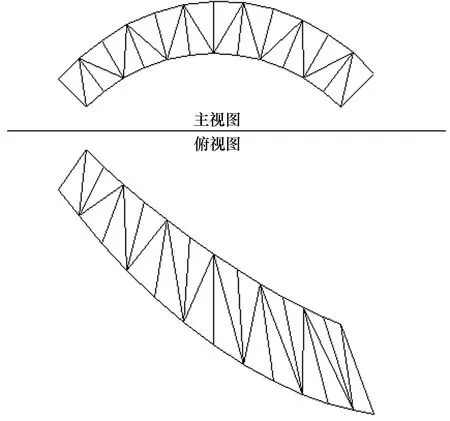
图6 原始图形要求
4 主要逻辑及实现
AutoCAD为二次开发提供了3种方式,分别是VBA脚本、AutoLisp脚本和ObjectARX库,其中:VBA脚本逐渐没落并在高版本中被抛弃;AutoLisp脚本不太适合处理复杂问题;ObjectARX库最为强大,可以访问部分VBA脚本和AutoLisp脚本无法访问的对象,需要C++编程语言支撑。由于曲面展开过程中涉及较复杂的数据结构和运算,在此使用C++编程语言基于ObjectARX库对AutoCAD进行二次开发较为方便高效,根据文章第2部分编写AutoCAD自动批量求直线实长的程序,程序流程图如图7所示。
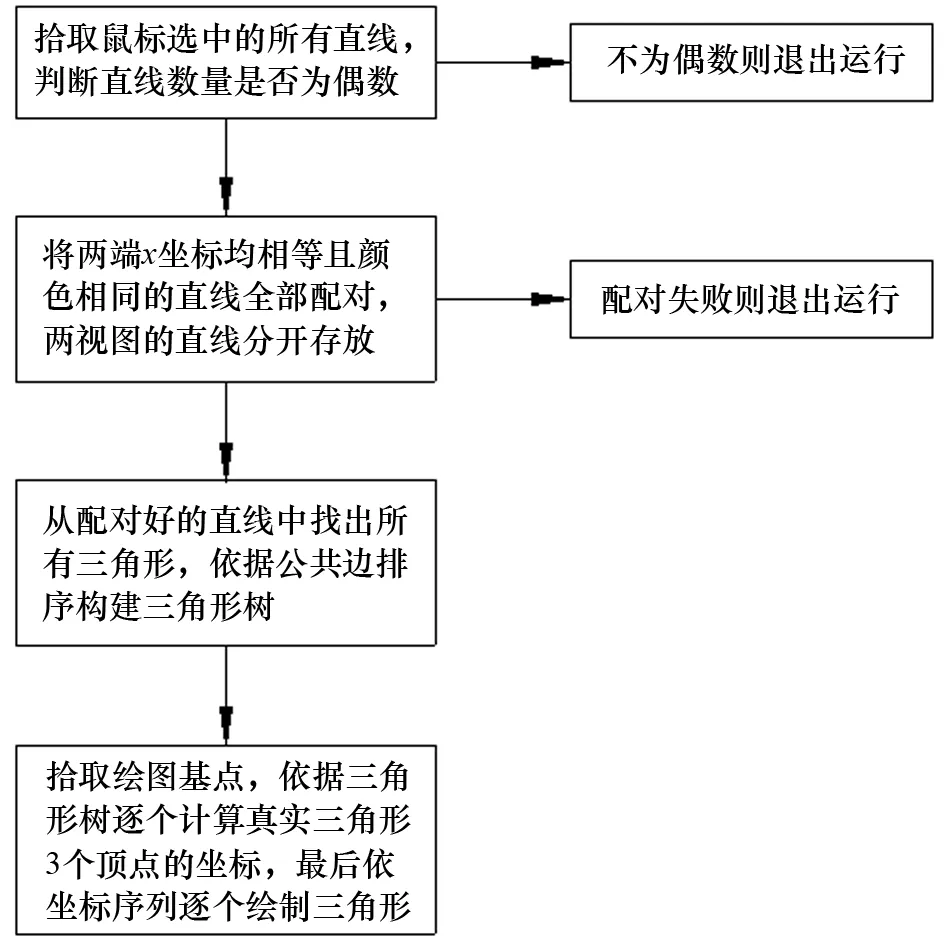
图7 程序流程图
(1) 拾取用户所选的直线。
long nLength;
ads_name ssLines;
struct resbuf eb1;
wchar_t sbuf1[10] = {0};
eb1.restype=0; //实体名
lstrcpy(sbuf1,_T("LINE"));
eb1.resval.rstring=sbuf1;
eb1.rbnext=NULL;
acdbHostApplicationServices()->workingDatabase();
acutPrintf(_T(" Select lines: "));
int stat = acedSSGet(NULL,NULL,NULL,&eb1,ssLines);
if ((stat == RTERROR)||(stat == RTCAN))
{
acutPrintf(_T(" User select canceled. "));
return;
}
acedSSLength(ssLines, &nLength);
if (nLength %2 != 0) //判断所选择的直线的数目是否为偶数
{
acutPrintf(_T(" Error! Line Number is not even number. "));
return;
}
(2) 将两端点x坐标均相等且颜色相同的直线配对存放。
typedef struct _PAIR_LINE //配对成功的2条线
{
AcGePoint3d pt1; //Line1 存放主视图直线
AcGePoint3d pt2;
AcGePoint3d pt3; //Line2 存放俯视图直线
AcGePoint3d pt4;
}PAIR_LINE,*PPAIR_LINE;
(3) 从配对好的直线组中找出三角形存放于三角形结构体。
typedef struct _TRANGLE //三组线组成的三角形
{
int nId; //nId表示三角形序号
bool bCenter; //用来指示当前三角形是否曾经为中心三角形
PAIR_LINE pl1; //配对成功的3组线
PAIR_LINE pl2;
PAIR_LINE pl3;
AcGePoint3d pt1; //主视图中三角形的3个点
AcGePoint3d pt2;
AcGePoint3d pt3;
AcGePoint3d pt4; //俯视图中三角形的3个点
AcGePoint3d pt5;
AcGePoint3d pt6;
}TRANGLE,*PTRANGLE;
每次以当前三角形为中心,依据公共边构建三角形树:
typedef struct _TRANGLE_TREE //构建三角形树,绘三角形时遍历
{
TRANGLE stTrangleNode; //当前三角形
struct _TRANGLE_TREE* ptt[3]; //与当前三角形共一条边的三角形
_TRANGLE_TREE()
{
for ( int i = 0 ; i < 3 ; i ++ )
{
ptt[i] = NULL;
}
}
}TRANGLE_TREE,*PTRANGLE_TREE;
(4) 依据绘图基点和三角形树逐个计算真实三角形顶点坐标。
typedef struct _REAL_TRANGLE //真实三角形
{
int nId; //三角形ID,与相应原三角形的ID相等
bool bReady; //顶点坐标是否已经计算完毕
bool bDrawed; //是否已经绘图
bool bCenter; //是否曾经作为中心三角形
double tb1; //3条边实长
double tb2;
double tb3;
AcGePoint3d pt1; //3个顶点的坐标
AcGePoint3d pt2;
AcGePoint3d pt3;
_REAL_TRANGLE()
{
tb1 = 0.0;
tb2 = 0.0;
tb3 = 0.0;
}
}REAL_TRANGLE,*PREAL_TRANGLE;
需要注意的是,遍历三角形树计算真实三角形时(见图8),下面的三角形为当前三角形,以当前三角形为中心去遍历计算具有公共边的三角形时,若以图8中水平边为公共边,分别以两端点和两边长画圆求交点,实际上会得到2个交点,这时用AutoCAD自带的IntersectWith函数得到圆的2个交点后应该去掉与当前三角形同一侧的顶点。
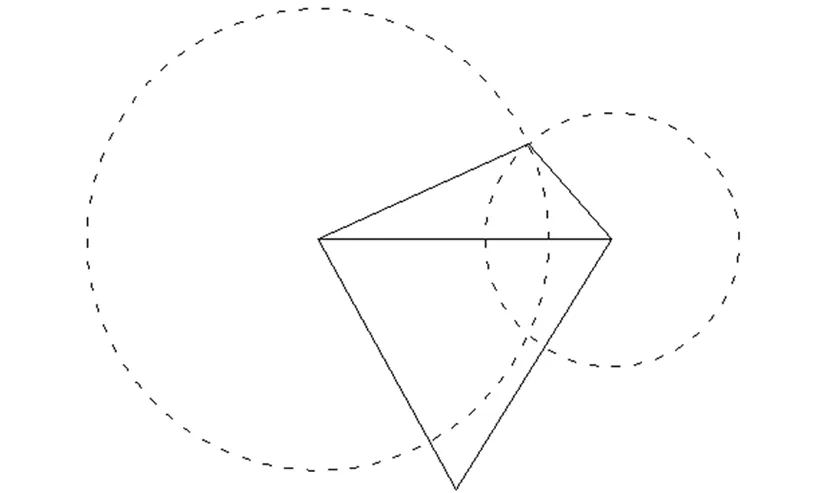
图8 遍历三角形树
(5) 调用CAD函数绘图,将实体添加到图形数据库中的模型空间绘制出来。
5 程序编译及运行
将源代码通过Visual Studio编译器编译生成.arx插件,在AutoCAD中使用ap命令加载插件,输入注册的CAD命令运行。如图9所示,选中主视图和俯视图中的所有三角形,然后确定绘图基点,程序自动绘制出展开图。
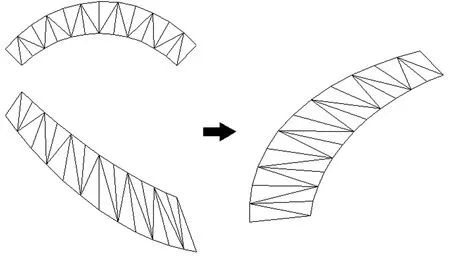
图9 某船型锚台半边图形展开
6 结 语
根据三角线法展开原理,对AutoCAD进行二次开发,实现批量自动求直线实长的功能,经测试,在锚台、侧推、曲面开孔放样下料中均可行。在实际应用中,对比原完全手动展开曲面的方式,可以节省约80%的工作量,并且确保了直线实长的准确性。需要注意的是,由于程序将3个顶点x坐标均相等的三角形判定为1组三角形,即同一个真实的三角形在主视图和俯视图中的投影, 并辅以直线颜色的判断,故划分三角形时不要使得三角形的边呈铅垂状态,对于类似锚台的环形曲面,本文示例则根据对称性只放样一半曲面,放样完成后再根据对称性补全。对于复杂的不可展曲面,需要手动分割成几块以便近似处理,否则展开图会出现裂缝。
在很长一段时间里,设计人员总是依据放样原理进行手工放样,不仅耗时而且设计人员的经验技艺难以传承下来,设计停留在经验阶段而无法迈向更高阶段,工作效率难以整体性提升。若将经验技艺升级为程序化、知识库化、系统化,则无疑有助于整体工作效率的稳定提升,三角线法程序化展开曲面正是一种尝试。
[1] 宋延杭, 王川, 李永宣. ObjectARX实用指南——AutoCAD二次开发[M] . 北京:人民邮电出版社, 1999.
[2] 徐荣璋, 刘晓毅, 陈军. 曲面展开方法的发展现状[J].模具技术, 2002(5):15-18.
[3] 余勇. 船舶曲面分段外板重构及其展开技术研究[D] . 镇江: 江苏科技大学, 2016.
[4] 潘炜, 吴慧, 李铁瑞,等. 基于曲面展开的自由曲面网格划分[J] . 浙江大学学报(工学版), 2016,50(10):1973-1979.
[5] 罗振华, 蒋芬, 蒋威. 针对不可展曲面的近似展开方法浅析[J] . 科技创新导报, 2014(30):51.
[6] 蒋威. 不可展曲面的近似展开及其应用[D] . 上海: 复旦大学, 2013.
[7] 肖雄, 黄朝炎, 胡勇,等. 三维曲面船体外板数学展开方法研究[J] . 船舶工程, 2013, 42(1):74-77.
[8] 阎佩佳, 薛卓, 张育丹. 复杂曲面展开[J]. 科技致富向导, 2012(14):366.

