“121”三段四环导学课堂教学模式的课型研究
——概念课的教学模式案例分析
翟彩云 张 勇 陈武钊
(广东省广州市增城区新塘中学,广东 广州)
概念教学是数学教学中不可缺少的重要组成部分。概念教学是一个“重新建构”过程,是一个“意义赋予”过程。“121”三段四环导学课堂教学模式中概念课的教学过程可概括为下图:

案例:函数的单调性(第一课时)
函数的单调性是函数的重要性质。其中增函数、减函数的概念是形式化定义,较为抽象,学生不易理解,可采用概念形成的教学方式。
一、概念的引入(约10分钟)
(一)重现已有知识
师:在初中我们已经学习过一次函数、二次函数、反比例函数的图象和性质。现在请同学们观察下列函数的图象,并说明函数值y随x的增大而怎样变化?
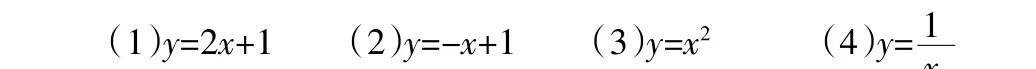
图1
学生可能有以下回答:
(1)函数y=2x+1在定义域内y随x的增大而增大。
(2)函数y=-x+1在定义域内y随x的增大而减小。
(3)函数 y=x2在[0,+∞)上 y随 x的增大而增大,在(-∞,0]上y随x的增大而减小。
(4)函数在(0,+∞)和(-∞,0)上y都随x的增大而减少。
(设计意图:观察具体函数图象特征,注重直观感知)
师:这些例子都反映了自变量变化时函数值也会发生改变,有的变大,有的变小,这是函数的一个重要性质,称为函数的单调性。同学们在初中对函数的这种性质虽然有所了解,但是没有严格的定义,今天我们的学习任务就是建立函数单调性的严格定义。
(二)引入新的概念
问题1:你能不能根据自己的理解说说什么是增函数、减函数?
学生可能回答:如果函数f(x)在某个区间随自变量x的增大,y也越来越大,我们说函数f(x)在该区间上为增函数;如果函数f(x)在某个区间随自变量x的增大,y反而越来越小,我们说函数f(x)在该区间上为减函数。
师:这种认识从图象的直观性很容易得到,即是从“形”的角度对函数单调性的直观性认识。
(设计意图:从图象直观感知函数单调性,完成对函数单调性的感性认识。)
问题2:如何从“数”的角度,对“函数值y随x的增大而增大(或减少)的特征”给予具体的定量刻画呢?以y=x2在[0,+∞)上是增函数为例,你能列举一些数据予以说明吗?
学生可能回答:当 x=0时,y=0;当x=1时,y=1;当x=2时,y=4……
问题3:这样的数据能列举完吗?你能用准确的数学符号语言表达出增函数的定义吗?
学生回答:不能。
老师:为什么不能呢?
逐步启发学生找到问题的根源:自变量不可能被穷举,从而逐步回答出:对任意的两个自变量 x1,x2∈[0,+∞),x1<x2,因为即即f(x1)<f(x2),所以f(x)=x2在[0,+∞)上为增函数。
(设计意图:引导学生思考讨论,把对单调性的认识由感性认识上升到理性认识的高度。事实上也给出了证明单调性的方法,为典例1的学习做好铺垫。)
(三)形成概念定义
(教师用投影展示)一般地,设函数f(x)的定义域为I:
如果对于定义域I内某个区间D上的任意两个自变量x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说f(x)在区间D是增函数,区间D为y=f(x)的单调增区间。(图2)
如果对于定义域I内某个区间D上的任意两个自变量x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说f(x)在区间D是减函数。区间D为y=f(x)的单调减区间。(图3)
如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间。

图2
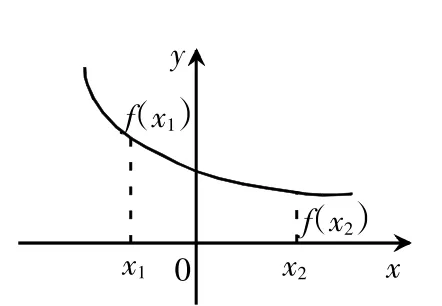
图3
二、概念的理解(约20分钟)
(一)探究概念等价变换
师:由不等式性质知:若 a<b 则 a-b<0;若 a>b 则 a-b>0,反之亦然。要比较f(x1)与f(x2)的大小,只要观察f(x1)-f(x2)<0?或f(x1)-f(x2)>0?因此,单调性的定义你能作出怎样的等价变换呢?
学生:对任意的两个变量x1,x2∈I,x1<x2有f(x1)-f(x2)<0,则称函数f(x)在区间I单调递增。
学生:对任意的两个变量x1,x2∈I,x1<x2,有f(x1)-f(x2)>0,则称函数(fx)在区间I单调递减。
(二)概念理解的变式练习
师:分别指出各函数(1)y=2x+1;(2)y=-x+1;(3)y=x2;(4)y=的单调区间。
学生可能回答:(1)函数 y=2x+1只有增区间(-∞,+∞);(2)函数 y=-x+1只有减区间(-∞,+∞);(1 3)函数y=x2的增区间是[0,+∞),减区间是(-∞,0];(4)函数的减区间为(-∞,0)和(0,+∞)。
问题4:能把函数的减区间(-∞,0)和(0,+∞)改写成(-∞,0)∪(0,+∞)吗?
一些学生回答可以,一些学生回答不可以。
师:请认为-1不2可∈以-的∞同0学∪说说0理∞由。-1<2f-1>f2学生甲:f,-1(<f2,)( ,),并且 ,应该是( )(),这与事实( )()矛盾。
师:甲同学说对了。一个函数∪同时有两个或以上的增(或减)区间要用“,”或“和”分开,不能用“ ”把各个单调区间连接起来,这是求函数的单调区间中最常见、最典型的错误,请同学务必注意。
(设计5意图:规范表达,防止典型错误的发生)
问题:请回答下面几个思考题
①已知因为 (f-1)<(f2),所以函数 (fx)是增函数,对吗?
②若函数在区间(1,2]和(2,3)上均为增函数,则函数(fx)在区间(1,3)上为增函数,对吗?
③因为函数在区间(-∞,0)和(0,+∞)上都是减函数,所以在定义域上是减函数,对吗?学生可能回答:都不对。师①:通过以上几个小x题的x讨论交流,我们得出以下结论:单调性定义中的1,2是区间内任意两个值,而不是特殊的两个②值。单调性是对定义域内某个区间而言的,离开了定义域和相应区间③就谈不上单调性,单调性是函数A的B局部性质。
函数在定义域A内∪的B两个区间 , 上都是增(或减)函数,一般不能认为函数在 上是增(或减)函数。
(设计意图:让学生由特殊到一般,从具体到抽象归纳出单调性的定义,通过几个思考题的辨析,加深学生对定义的理解)
(三)典例合作探究(交流研讨、展示点评、点拨整理)
例1.证明函数在(1,+∞)上是增函数。
1.分析解决问题
针对学生可能出现的问题,组织学生讨论、交流、展示、点评、质疑。
证明:任取且取值

∴ 函数在(1,+∞)上是增函数。 下结论
2.归纳解题步骤
引导学生归纳证明函数单调性的步骤:取值、作差、变形、判断符号、下结论。
(设计意图:初步掌握根据定义证明函数单调性的方法和步骤)
三、概念的运用(约10分钟)
1.证明函数f(x)=x2+1在[0,+∞)上是增函数。
2.对任意的两个变量x1,x2∈I,x1<x2如果有能判断函数f(x)在区间上是增函数吗?
(设计意图:通过练习1,巩固学习效果,练习2拓展学生思维)
四、总结提高
学生交流在本节课学习中的体会、收获,交流学习过程中的体验和感受,师生共同完成小结。
(一)小结
(1)探究得到函数单调性的概念。
(2)单调性的证明方法和步骤:取值、作差、变形、判断符号、下结论。
(3)数学思想方法:数形结合。
(二)作业
书面作业:课本第 39页,习题 1.3,第 1,2,3题。
选做作业:讨论函数的单调性。
五、案例点评
函数的单调性是函数的重要且基本的性质。函数的单调性从图象角度来看,清楚、直观,容易理解,但是用抽象的数学符号语言来刻画,即当x1,x2∈I,x1<x2都有f(x1)<f(x2),则f(x)在区间I上是增函数,当x1,x2∈I,x1<x2,都有f(x1)>f(x2),则f(x)在区间I上是减函数,对刚进高一的学生来说,就显得比较抽象。本案例针对函数单调性概念的形式化定义这一难点,教师通过学生初中已接触过的基本初等函数:一次函数、二次函数、反比例函数的图象与性质,引入课题,为新概念的学习创设情境,一定程度上达到承上启下的效果,为提高课堂效率打下良好基础。从已经掌握的一些简单函数的图象入手,让学生在问题情境中认识从“形”的直观性过渡到从“数”的角度上对函数单调性的特征进行辨析。在形成概念的过程中,紧扣概念中的关键语句,通过概念的变式思考、概念理解的变式练习、典例“证明函数f(x)=x+1 x在(1,+∞)上是增函数”的分析加深学生对单调性这个概念的理解,突破了如何用定义进行解题这一难点,并指出学生做题中最典型并且最常见的一个错误(一个函数同时有两个或以上的增〈或减〉区间要用“,”或“和”分开,不能用“∪”把各个单调区间连接起来),教师板书了规范的解答过程,师生一起总结解题的步骤。最后,通过概念的运用环节,让学生学以致用。通过解决:对任意的两个变量x1,x2∈I,x1<x2,如果有能判断函数f(x)在区间I上是增函数吗?达到拓展提升的目的。整节课学生都能主动参与课堂,顺利形成准确概念,使“单调性”顺利融入学生的知识体系。
[1]肖凌戆.高中数学“优效教学”的理论与实践[M].陕西师范大学出版社,2015.
[2]葛永.提高数学试卷评讲有效性的探索[J].高中数学教与学,2012(12):1-3.
[3]穆镇海.如何引导学生积极参与数学学习过程[J].中学数学教与学,2015(4):5-8.

