交换环的w-弱finitistic维数的注记
李 庆
(西南民族大学计算机科学与技术学院,四川 成都 610041)
1 引言及准备知识
Glaz和Vasconcelos在文献[1]中引入了semi-divisorial模的定义.semi-divisorial模推广了divisorial模和内射模.Wang和McCasland在文献[2]中改进了semi-divisorial模,并定义了semi-divisorial包络(即w-包络),形成了w-算子.这一算子在乘法理想理论和模理论中有重要的应用.文献[3-7]成功地将w-算子运用到内射模、平坦模和投射模的研究中.另外,Prufer整环在经典的理想理论中发挥着举足轻重的作用.从同调代数的角度看,Prufer整环就是弱整体维数小于等于1的整环.Wang和Qiao在文献[4]中利用w-算子给出了交换环上w-平坦维数和w-弱整体维数w-w.gl.dim(R)的定义,并证明了PvMD实际上就是w-w.gl.dim(R)≤1的整环.众所周知,PvMD是Prufer整环的一类重要推广的整环.以此为启发,利用w-算子引入交换环上w-投射维数的概念并研究它的应用.
恒设R是具有单位元的交换环,E(M)是R-模M的内射包.设J是R的理想.根据文献[8],如果J是R的有限理想且自然同态φ:R→J*=HomR(J,R)同构,则称J是R的GV-理想.R的GV-理想的集合记为GV(R).实际上,GV(R)是环R的理想乘法系.定义torGV(M)={x∈M|存在J∈GV(R)使得Jx=0}.易知torGV(M)是M的子模.称R-模M为GV-挠模(或GV-无挠模),是指torGV(M)=M(torGV(M)=0).
注意,R-模M是GV-挠模当且仅当对任意的m∈w-Max(R),Mm=0.w-Max(R)记为R的所有极大w-理想集合.称GV-无挠R-模M是w-模,是指对任意的J∈torGV(R),E(,M)=0.对任 意 的 GV-无 挠R-模M,Mw={x∈E(M存在J∈GV(R)使得Jx⊆M}是包含M的E(M)的w-子模,称为M的w-包络.显然,GV-无挠R-模M是w-模当且仅当Mw=M.更多关于w-模的性质和所涉及的概念和术语请参见文献[8-13].
2 w-投射维数
设M,N是R-模,f:M→N是R-模同态.根据文献[10],称f是w-单同态(或w-满同态或w-同构),是指对任意的m∈w-Max(R),fm:Mm→Nm是单同态(或满同态或同构).模同态序列A→B→C是w-正合列,是指对任意的m∈w-Max(R),模同态序列Am→Bm→Cm是正合列.R-模M是有限型模,是指存在w-正合列F→M→0,其中F是有限生成自由R-模.R-模M是有限表现型模,是指存在w-正合列F1→F0→M→0,其中F1,F0是有限生成自由R-模.由文献[14],R-模M是w-平坦模,是指对任意的w-单同态f:A→B,1⊗Rf:M⊗RA→M⊗RB是w-单同态.显然,平坦模和GV-无挠模都是w-平坦模.令由文献[3],R-模M是w-投射模,是指对任意无挠的w-模N,Ext1R(L(M),N)是GV-挠模.下面给出w-投射分解和w-投射维数的定义.
定义2.1 设M是R-模,如果有w-正合列…→Pn→Pn-1→…→P1→P0→M→0,其中Pi都是w-投射模,则称该w-正合列是R-模M的w-投射分解.
定义2.2设M是R-模,如果有w-投射分解…→Pn→Pn-1→…→P1→P0→M→0,则称M有有限的w-投射维数.并通俗地说M有长度不超过n的w-投射分解.当有有限的w-投射维数时,M的最短的投射分解的长度称为M的w-投M射维数,用wpdR(M)表示.如果M没有有限长度的w-投射分解,则记w-pdR(M)=∞.
显然,若M有一个长度为n的w-投射分解,则有w-pdR(M)≤n.
w-pdR(M)=0当且仅当M是w-投射模.因为投射模是w-投射模,正合列是w-正合列,因此wpdR(M)≤pdR(M).
定义2.3设M是R-模,如果有w-正合列0→Pn→Pn-1→…→P1→P0→M→0,其中Pi都是有限型的w-投射模,则称M有有限w-投射分解.此时显然有w-pdR(M)<∞.
注若M有有限w-投射分解,则M是有限表现型模.实际上,若M有有限w-投射分解0→Pn→Pn-1→…→P1→P0→M→0,则对任意m∈w-Max(R),由文献[3]中 Theorem2.5有正合列0→(Pn)m→(Pn-1)m→…→(P1)m→(P0)m→Mm→0,其中(Pi)m是有限生成自由模,i=0,1,2,…,n.故M是有限表现型模.
定义2.4设R是交换环,令w-fPD(R)=sup{w-pdR(M)有有限w-投射分解}称之为R的w-弱 finitistic维数.
定理2.5下列命题等价:
(1)w-fPD(R)=0;
(2)若0→K→P→F→0是w-正合列,其中K,P是有限型的w-投射模,则F是有限表现型的w-投射模.
(3)若M有有限w-投射分解,则M是w-投射模.
证明(1)⇒(2)设w-fPD(R)=0.因0→K→P→F→0是w-正合列,其中K,P是有限型的w-投射模,故F有有限w-投射分解.由于w-fPD(R)=0,于是w-pdRF=0,从而F是w-投射模.由文献[3]中Theorem2.5,对任意m∈w-Max(R)有正合列0→Km→Pm→Fm→0是正合列,其中Km,Pm是有限生成自由模,故F是有限表现型模.
(2)⇒(1)设M有有限w-投射分解,不妨设w-pdRM=n<∞,故存在一个w-正合列故对任意m∈w-Max(R)有正合列令是w-正合列,这里Pn,Pn-1都是有限型的w-投射模 . 因此,Kn-2是有限表现型的w-投射模 . 故 0 →Kn-2→Pn-2→…→P1→P0→M→0是M的有限w-投射分解.从而w-pdRM≤n-1<n,矛盾.故w-fPD(R)=0.
(1)⇔(3)直接由w-弱finitistic维数的定义可得结论.证毕.
由文献[3]中Theorem 2.5和文献[14]中Theorem3.3可知,w-投射模是w-平坦模,反之,不成立.但是以下结论成立.
定理2.6有限表现型的w-平坦R-模M是w-投射模.
证明对任意m∈w-Max(R),Mm是有限表现型的平坦模.于是Mm是投射的Rm-模,从而Mm是自由模.由文献[3]中Theorem 2.5,M是w-投射模.证毕.
既然w-投射模是w-平坦模,因此w-fdRM≤wpdRM.
记f-Mod(R)={R-模M|M有有限w-投射分解}.
命题2.7设M∈f-Mod(R),n是一非负整数.则有
w-pdRM≤n当且仅当对任意m∈w-Max(R),pdRmMm≤n.
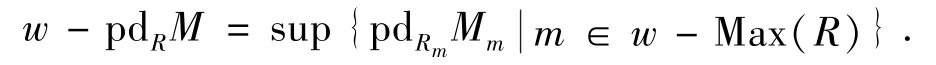
证明(1) 设0→Pn→Pn-1→…→P1→P0→M→0是M的一个有限w-投射分解,则对任意m∈w-Max(R),0→(Pn)m→(Pn-1)m→…→(P1)m→(P0)m→Mm→0是正合列.由文献[3]中Theorem2.19,有限型的w-投射模是是有限表现型的,故P0,…,Pn是有限表现型的 .由文献[3]中 Theorem2.8,Pi是w-投射模当且仅当对任意m∈w-Max(R),(Pi)m是投射模.于是,w-pdRM≤n当且仅当对任意m∈w-Max(R),pdRmMm≤n.
(2)直接由(1)可得结论.证毕.
显然,w-fPD(R)=sup{w-pdR(M)|M∈f-Mod(R)}=sup{pdRm(Mm)|m∈w-Max(R),M∈f-Mod(R)}.
3 某些环上w-弱finitistic维数的应用
由文献[10],R-模M是w-凝聚模,是指M是有限型模,且M的每个有限型模都是有限表现型的.环R是w-凝聚环,是指R作为R-模是w-凝聚模.
定理3.1设R是w-凝聚环,M是有限表现型模,则M有w-投射分解…→Pn→Pn-1→…→P1→P0→M→0,其中Pi是有限型的w-投射模,i=0,1,….
证明由文献[10]中Theorem 2.1,存在一个w-正合列0→K0→P0→M→0,其中P0是有限生成投射模,K0是有限型模.于是,对任意m∈w-Max(R),0→(K0)m→(P0)m→Mm→0是正合列,其中(P0)m是自由模,(K0)m是有限生成的.因R是w-凝聚环,故对任意m∈w-Max(R),Rm是凝聚环.因(K0)m是自由模(P0)m的有限生成子模,故(K0)m是有限表现型模.下证K0是有限表现型模.由于K0是有限型模,所以存在一个w-正合列0→I0→F0→K0→0,其中F0是有限生成自由模,I0是F0的子模.因此,对任意m∈w-Max(R),0→(I0)m→(F0)m→(K0)m→0是正合列.因(K0)m是有限表现型模,(F0)m是有限生成自由模,故(I0)m是有限生成模.因Rm是凝聚环,于是(I0)m是有限表现模.因此,存在一个正合列(F1)m→(I0)m→0,其中F1是有限生成自由R-模.从而有正合列(F1)m→(F0)m→(K0)m→0,于是F1→F0→K0→0是w-正合列,其中F0,F1都是有限生成自由R-模.因此,K0是有限表现型模.类似地,存在一个w-正合列0→K1→P1→K0→0,其中P1是有限生成投射模,K1是有限表现型模.因此,有如下正合列0→(K0)m→(P0)m→Mm→0和0→(K1)m→(P1)m→(K0)m→0.从而有正合列0→(K1)m→(P1)m→(P0)m→Mm→0,于是0→K1→P1→P0→M→0是w-正合列.继续以上过程,于是存在一个w-正合列…→Pn→Pn-1→…→P1→P0→M→0,其中Pi是有限生成投射模,从而Pi是有限型的w-投射模,i=0,1,….证毕.
从定理3.1证明过程中可知存在一个w-正合列0 →Kn-1→Pn-1→ … →P1→P0→M→0 ,其中P0,…,Pn-1是有限生成投射模,Kn-1是有限表现型模.
定理3.2设R是w-凝聚环,M是有限表现型模,则w-fdR(R)=w-pdR(R).
证明只需证明w-pdR(R)≤w-fdR(R).设w-fdR(R)=n.由定理3.1,存在一个w-正合列0→Kn-1→Pn-1→ … →P1→P0→M→0 ,其中P0,…,Pn-1是有限生成投射模,Kn-1是有限表现型模.由文献[4]中 Proposition 2.3,Kn-1是w-平坦模 . 由定理2.5,Kn-1是w-投射模 . 于是
w-pdR(R)≤n.从而w-pdR(R)≤w-fdR(R).
证毕.
回顾w-模M是w-Noether模,是指M满足M的w-子模的升链 条件.环R是w-Noether环,是指R作为R-模是w-Noether模.众所周知,w-模M是w-Noether模当且仅当M的每个子模都是有限型的.
根据文献[15],环R是w-半遗传环,是指R的每个有限型理想都是w-投射理想.注意,若环R是w-半遗传环,则对任意m∈w-Max(R),Rm是半遗传环.实际上,假设Im是Rm的有限生成理想,其中I是R的有限生成理想.由文献[12]中Theorem4.11,I是w-投射理想,从而由文献[3]中Theorem 2.4,Im是Rm的投射理想.于是Rm是半遗传环.
推论3.3设环R是w-Noether环,M是有限型的,则w-fdR(R)=w-pdR(R).
证明 若R是w-Noether环,则有限型的R-模是有限表现型的.既然w-Noether环是w-凝聚环,由定理3.2直接得出结论.证毕.
定理3.4设R是w-半遗传环,则w-fPD(R)≤1.
证明设M∈f-Mod(R),则M是有限表现型的.由文献[15],w-半遗传环是w-凝聚环.由定理3.1,存在一个w-正合列0→K→P→M→0,其中P是有限生成投射模,K是有限表现型模.于是,对任意m∈w-Max(R),0→Km→Pm→Mm→0是正合列,其中Pm是有限生成自由模,Km是Pm的有限生成子模.因Rm是半遗传环, 故Km是投射模.由文献[3]中Theorem 2.8,K是有限型的w-投射模.因此,w-pdR(M)≤1,从而w-fPD(R)≤1.证毕.
[1] GLAZ S,VASCONCELOS W V.Flat ideals II[J].Manuscripta Mathematica,1977,22:325-341.
[2] WANG F G,MCCASLAND R L.On Strong Mori Domains[J].Journal of Pure and Applied Algebra,1999,135(2):155-165.
[3] WANG F G,KIM H.Two generalizations of projective modules and their applications[J].Journal of Pure and Applied Algebra,2015,219(6):2099-2123.
[4] WANG F G,QIAO L.Thew-weak global dimension of commutative ring[J].Bulletin of the Korean Mathematics Society,2015,52(4):1327-1338.
[5] FUSACCHIA G.Injective modules and semistar operations[J].Journal of Pure and Applied Algebra,2012,216:77-90.
[6] KIM H,KIM E S,PARK Y S.Injective modules over strong Mori domains[J].Houston Journal of Mathematics,2008,34:349-360.
[7] 王芳贵,张俊.w-Noether环上的内射模[J].数学学报,2010,53(6):1119-1130.
[8] YIN H,WANG F G,ZHU X S,et al.w-modules over commutative rings[J].Journal of the Korean Mathematical Society,2011,48(1):207-222.
[9] WANG F G.Onw-projective modules andw-flat modules[J].Algebra Colloquium,1997,4(1):111-120.
[10] WANG F G.有限表现型模和w-凝聚环[J].四川大学学报(自然科学版),2010:33(1):1-9.
[11] 赵国,汪明义.关于极大内射性的注记[J].四川大学学报(自然科学版),2005,21(1):1451-1458.
[12] 王芳贵,汪明义,杨立英.交换环上的极大性内射模[J].四川师范大学学报(自然科学版),2010,33(3):277-285.
[13] 王芳贵.交换环与星型算子理论[M].北京:科学出版社,2006.
[14] KIM H,WANG F G.On LCM-stable modules[J].Journal of Algebra and its Applications,2014,13(4):1350133.
[15] WANG F G,KIM H.w-injective modules andw-semi-hereditary rings[J].Journal of the Korean Mathematical Society,2014,51(3):509-525.

