基于CVaR的逼近算法求解一类随机逆变分不等式
山述强,宋建成
(西南民族大学计算机科学与技术学院,四川 成都 610041)
1 引言
假定(Ω,ℑ,P)是一概率空间,〈.,.〉表示Rn空间的内积,K⊂Rn为非空闭凸子集,有限维空间中的随机逆变分不等式(SIVI(f,h))可以表示为:找x*∈Rn,满足
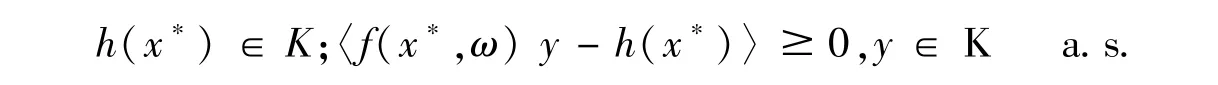
其中f:Rn×Ω→Rn,h:Rn→Rn为两向量值函数,a.s.表示在概率 P下几乎必然成立.
随机逆变分不等式可以被广泛的应用于交通均衡、网络经济均衡、物流供应链管理等实际问题.对于上述问题,由于模型受随机因素影响,一般很难求解,所以需要建立合理的模型求解随机逆变分不等式.
对于类似的问题,许多学者做了相应的研究.例如:Chen和Fukushima[1]研究了随机线性相补问题,并用期望残差极小化方法给出了随机线性相补问题的解;Fang、Chen和Fukushima[2]研究了随机线性相补问题的随机R0函数;Zhang和Chen[3]研究了随机非线性相补问题,并将其应用于交通均衡中;Luo和Lin[4]用期望残差极小化方法求解随机变分不等式问题;Ma和Huang[5]用期望残差极小化方法求解一类随机拟变分不等式问题.其它工作可参见于文献[6-13].
但是,如果将残差量看作损失,那么期望残差极小化方法并没有对风险加以考虑,所以仅仅极小化期望可能带来高风险,这使得随机逆变分不等式在网络经济,物流管理等领域中受到极大限制.为此,Chen和Lin[14]研究了关于基于CVaR的逼近算法求解了随机变分不等式,Ma和Huang[15]改进了Chen和Lin在文献[14]中的模型,并用改进后的模型研究了一类随机变分不等式.受上述学者的工作启发,将采用基于CVaR的逼近算法求解一类随机逆变分不等式问题.并用拟蒙特卡洛方法给出该问题的解.
2 预备知识
定义2.1函数g:Rn×Ω→R满足下面条件:
(1)∀x∈K,g(x,ω)≥0, a.s.;
(2)x*∈K,g(x*,ω)≥0 a.s.⇔x*是随机逆变分不等式的解;则称g为随机逆变分不等式在集合K上的间隙函数.
令X={x∈Rn:h(x)∈K}为SIVI(f,h)的可行集,则由文献[16]中引理2易得下面引理.
引理2.1定义函数其中0<α<1,则有下面结论:
① ∀x∈X,g(x,ω) ≥0,a.s.
②x*∈X,g(x*,ω)≥0 a.s.⇔x*是随机逆变分不等式的解;
③SIVI(f,h)等价于求解下面的优化问

其中Rα(x,ω)=h(x)-PK(h(x)-αf(x,ω)),PK表示在K上的投影.
由引理2.1可知gα(x,ω)为SIVI(f,h)的间隙函数,将称其为SIVI(f,h)的正则化间隙函数.
令φ(x,μ,ω)=μ+(1-β)-1[gα(x,ω)-μ]+,基于CVaR 的模型就是考察下面的优化问题:
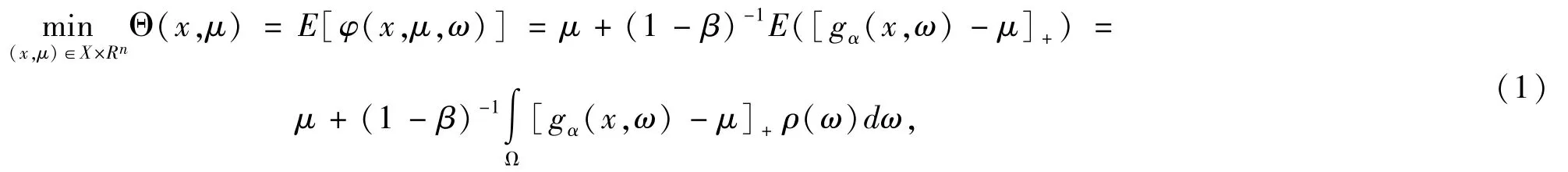
其中0<β<1,[t]+=max{t,0},ρ:Ω → [0,+∞) 为概率密度函数,并满足
对于给定的u>0,定义函数如下:
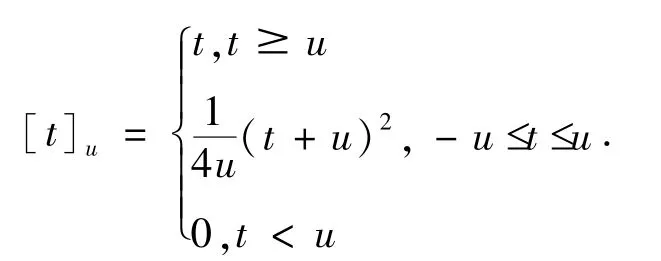
易证

引理2.2[15]对于任意的t,s,有下面结论:
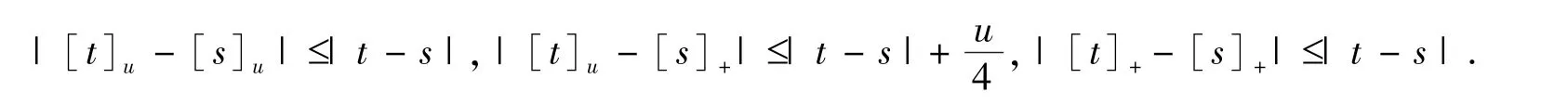
由于问题(1)包含数学期望,使得其求解变得极为困难.因此,将用拟蒙特卡洛方法给出问题(1)的解.考察下面的优化问题:

其中 Φ(x,μ,ω,u)=μ+(1-β)-1[gα(x,ω)-μ]u,Ωk={ωj∈Ω:j=1,2,…,Nk} 为观测集,当k→∞时,Nk→∞.
引理2.3[17]如果Φ(ω)在Ω上可积,那么
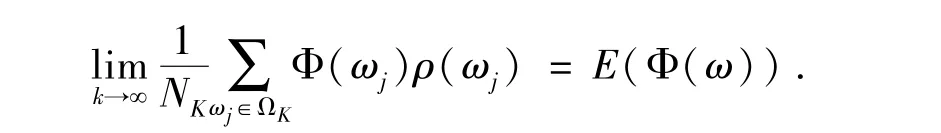
由引理2.1和文献[3]中的方法易得下面引理.
引理2.4 假定对于任意的ω∈Ω,f(.,ω)是连续可微的,h(x)连续可微,且满足对于x∈X,E(||f(x,ω)||2)<∞,E(||∇xf(x,ω)||2)<∞.那么,对于任意的ω∈Ω ,gα(x,ω)对于x也是连续可微的.特别的,对于任意的x∈X,ω∈Ω,有

3 主要结果
在这一节中,将给出优化问题(1)的解存在的一些充分条件,并在一定条件下求解出该问题.
定理3.1定义向量值函数M2(ω),N2(ω)如下:
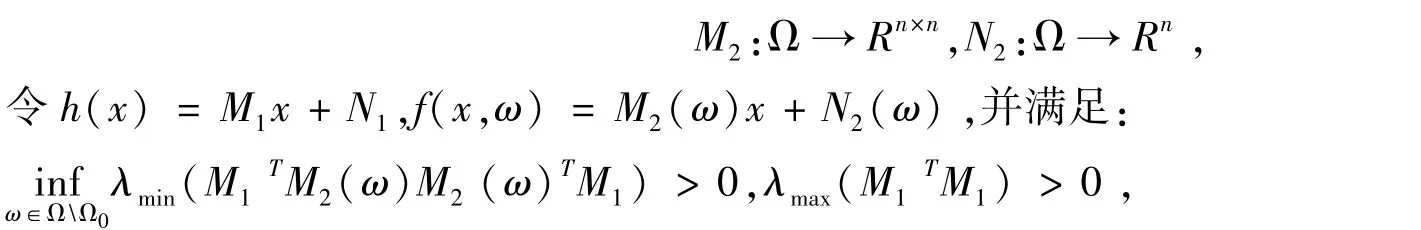
其中Ω0表示Ω的一个零测集.若分别用λmin(G),λmax(G)表示对称矩阵G的最小和最大特征值.那么,下列结论成立:
(i)如果,那么,对于几乎处处的ω∈Ω,gα(.,ω)为一凸函
数;进一步的,优化问题(1)为一凸优化问题.
(ii)如果,那么,对于几乎处处的ω∈Ω,gα(.,ω)为一强凸函数.优化问题(1)中目标函数Θ(x,μ)是关于x的强凸函数.
证明:(i)由[15]中定理1可知,对于任意的半正定矩阵A,
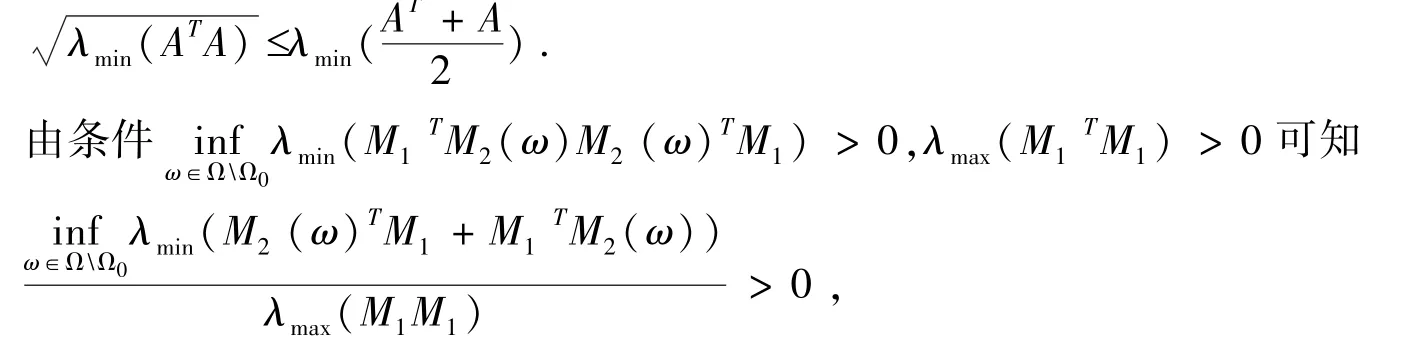
所以α是良定义的.
因为,由(3)式可知,对于任意的y,几乎处处的ω∈Ω,
h(.,y,ω)的Hessen矩阵是半正定的,所以对于任意的y,几乎处处的ω∈Ω,h(x,y,ω)是关于x的凸函数.由gα(x,ω)的定义可知对于几乎处处的ω∈Ω,gα(x,ω)是关于 x的凸函数,进而可知优化问题 (1)是凸优化问题.
(2)由(3)式可知,当时,对于任意的y,几乎处处的ω∈Ω,h(.,y,ω)的Hessen矩阵是正定的,那么对于任意的y,几乎处处的ω∈Ω,h(x,y,ω)是关于x的强凸函数,所以对于几乎处处的ω∈Ω,gα(x,ω)是关于x的强凸函数,进而可知优化问题 (1)中目标函数Θ(x,μ)是关于x的强凸函数.
注3.1:由定理3.1和[18]中定理3.2、定理3.3可知,当Θ(x,μ)满足一定条件时,优化问题(1)有解.
定理3.2定义函数M2:Ω →Rn×n,N2:Ω →Rn,假定h(x)=M1x+N1,
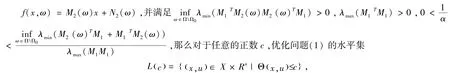
有界.
证明.由定理3.1可知,E(gα(x,ω))是强凸函数.那么
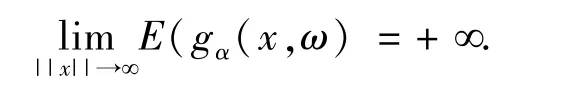
假设存在c*使得Lc*( )无界.那么存在(xk,μk)⊆Lc*( )满足:
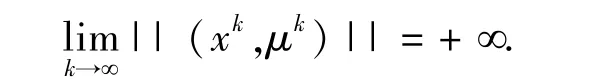
由Lc()和Θ(x,μ)的定义可知,对于任意的 k,有

和

因为进而可知,对于任意的 k,μk有界,所以
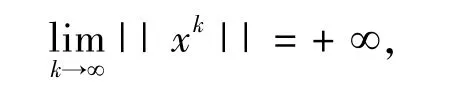
从而有

这与c*有界矛盾.所以,对于任意的正数c,Lc()有界.
定理3.3令h(x)=M1x+N1,f(x,ω)=M2(ω)x+N2(ω),并满足:
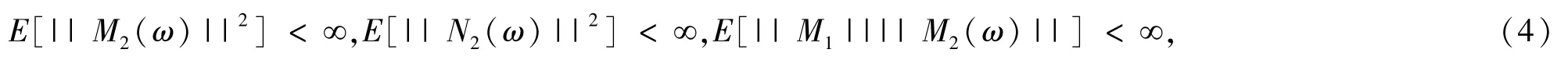
如果(xk,μk)为优化问题 (2)的最优解,则(xk,μk)的所有聚点都是优化问题 (1)的最优解.
证明:不妨假设(x*,μ*)是(xk,μk)的聚点,即(xk,μk)→(x*,μ*)∈X×Rn,在此将分三步证明定理成立.
首先,证明对于任意的(x,μ)∈X×Rn,下面式子成立:
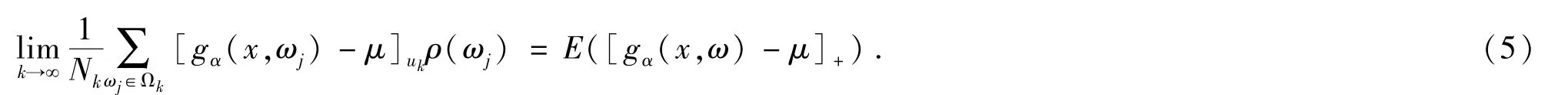
由引理2.2知
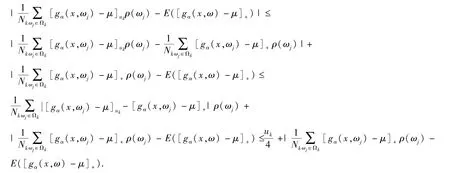
因为,所以上式收敛于0,进而可知(5)式成立.
其次,证明
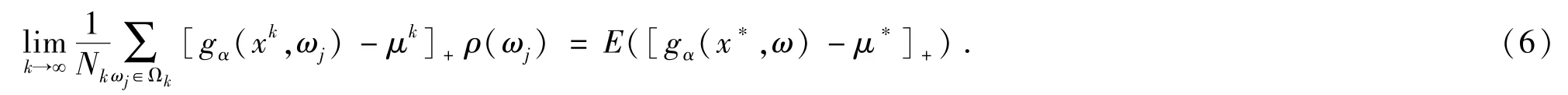
由中值定理可知
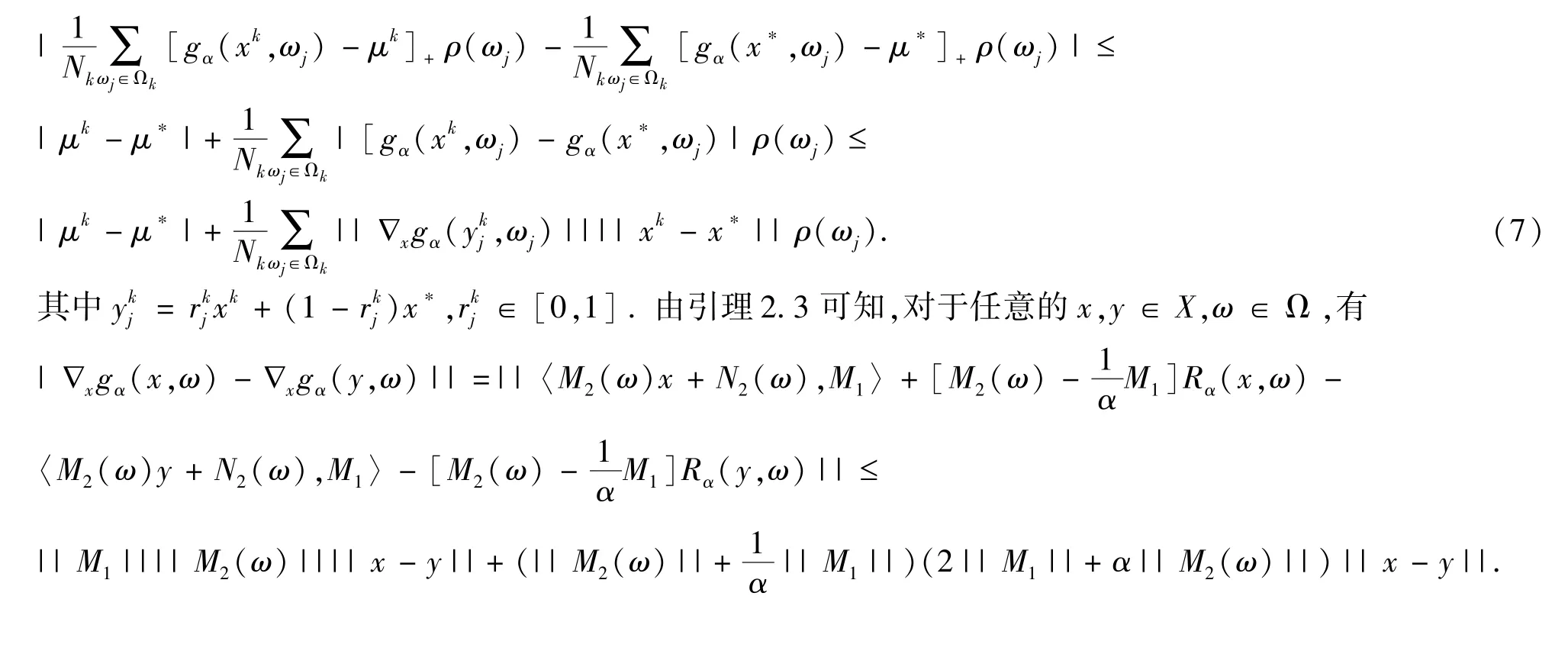

所以由(4)式可知下面式子成立:
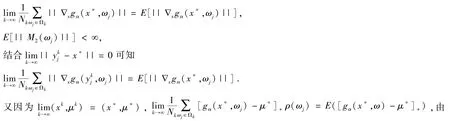
(7)式可知(6)式成立.
由引理2.2可知,下式成立:
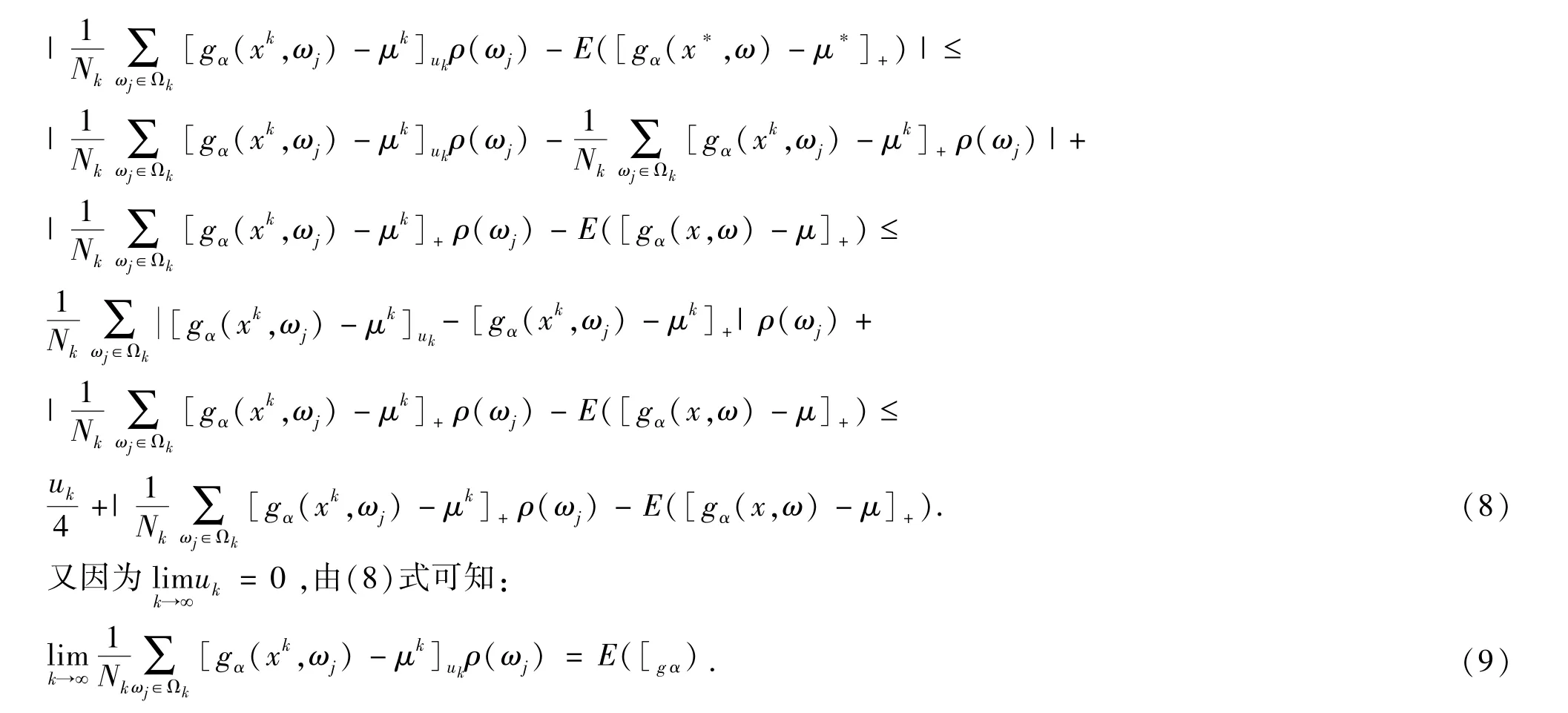
最后,证明(x*,μ*)是优化问题(1)的解.
因为(xk,μk)是优化问题 (2)的解.所以,对于任意的(x,μ)∈K×Rn,有
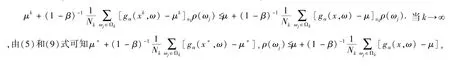
ρ(ωj),所以,(x*,μ*) 是优化问题(1)的解.
注3.2 由定理3.3可知,优化问题(1)的解可以先通过求解优化问题(2)的解,再用定理3.3的逼近算法求得.
注3.3 定理3.3的结果是对文献[14]中定理2的推广.当h(x)=x时,定理3.3将退化为文献[14]中的定理2.
[1] CHEN X J,FUKUSHIMA M.Expected residual minimization method for stochastic linear complementarity problems[J].Mathematics of Operations Research,2005,30:1022-1038.
[2] FANG H,CHEN X J,FUKUSHIMA M.Stochastic$R_0$matrix linear complementarity problems[J].SIAM Journal on Optimization,2007,18:482-506.
[3] ZHANG C,CHEN X J.Stochastic nonlinear complementarity problem and applications to traffic equilibrium under uncertainty[J].Journal of Optimization Theory and Applications,2008,137:277-295.
[4] LUO M J,LIN G H.Expectted residual minimization method for stochastic variational inequality problems[J].Journal of Optimization Theory and Applications,2009,140:103-116.
[5] MA H Q,HUANG N J.Expected residual minimization method for a class of stochastic quasivariational inequality problens[J].Journal of Applied Mathematics,2012,2012:doi:10.1155/2012/816528.
[6] LIN G H,FUKUSHIMA M.New reformulations for stochastic nonlinear compelementarity problems[J].Optimization Methods and Software,2006,21:551-564.
[7] JANG H,XU H.Stochastic approximation approaches to the stochastic variational inequality problems[J].IEEE Trans Automat Control,2008,53:1462-1475.
[8] LUO M J,LIN G H.Convergence results of the ERM method for nonlinear stochastic variational problems[J].Journal of Optimization Theory and Application,2009,142:569-581.
[9] MA H Q,WU M,HUANG N J,et al.Expected residual minimization method for stochastic variational inequality problem with nonlinear perturbations[J].Applied Mathematics and Computation,2013,219:6256-6267.
[10] CHEN X J,WETS J B,ZHANG Y F.Stochastic variational inequalities:residual minimization smoothing sample average approximations[J].SIAM Journal of Optimization,2012,22:649-673.
[11] CHEN X J,ZHANG C,FUKUSHIMA M.Robust solution of monotone stochastic linear complementarity problems[J].Mathematical Programming,2009,117:51-80.
[12] LUO M J,LIN G H.Stochastic variational inequality problems with additional constraints and their applications in supply chain network equilibria[J].Pacific Journal of Optimization,2011,7:263-279.
[13] MA H Q,WU M,HUANG N J.Expected residual minimization method for stochastic variational inequality problem with nonlinear perturbations[J].Applied Mathematics and Computation,2013 219:6256-6267.
[14] CHNE X J,LIN G H.CVaR-based formulation and approximation method for a class of stochastic variational inequality problems[J].Numerical Algebra,Control and Optimization,2011,1:35-48.
[15] MA H Q,HUANG N J.CVaR-based formulation and approximation method for a class of stochastic variational inequality problems[J].Mathematical inequalities and Applications,2013,16:981-998.
[16] D.Aussel,R.Guptab and A.Mehrab,Gap functions and error bounds for inverse quasi-variational inequality problems,Journal of Mathematical Analysis and Applications,2013,407,270-280.
[17] .PATRICK B.Probability and Measure[M].New York:Wiley Interscience,1995.
[18] M.Fukushima.非线性最优化基础[M].林桂华,译.北京:科学出版社,2011.

