基于直方图匹配的艺术Mosaic图像并行拼贴

宋 磊，朱晓强，叶翰辰，史 璇，朱梦尧，王向阳

(上海大学a.通信与信息工程学院；b.智慧城市研究院，上海200444)

对于由若干子图拼贴生成的新图，若从远、近观察可分别看出Mosaic效果图像和内容丰富的子图像，则称该类图像为艺术Mosaic图像。艺术Mosaic是最古老的装饰艺术之一，教堂常用瓦砾、玻璃等拼贴艺术Mosaic[1]。目前艺术Mosaic拼贴技术已广泛用于广告宣传、绘画艺术、视频影像等行业，如采用艺术Mosaic拼贴技术拼贴装饰性瓦片艺术品[2]，基于统拼贴风格[3-6]或数字蒙太奇风格[7-10]拼贴照片集锦等。1996年Robert[11]第一次提出艺术Mosiac图像智能拼贴，后有学者对其改进，如Finkelstein等[12]使用平移及缩放规则基于颜色均值法对拼贴图像进行颜色校正，但算法中使用传统半色调法，易产生人工周期纹理，且整体拼贴耗时较长；Zhang[13]用两种不同颜色空间的颜色匹配方法对其Mosaic图像拼贴效果进行了对比分析，认为可采用其他更佳方法挑选匹配的子图像，而现多数学者采用颜色均值法完成原图像与子图像的匹配[14-15]；Fujisawa等[16]构建基于GPU(graphic processing unit，图形处理器)的艺术Mosaic拼贴交互系统，拼贴时长从数分钟缩短至0.05 s，且实现了可交互的图像递归式拼贴，但使用的颜色匹配法导致远观艺术Mosaic图像具有明显的颗粒感。

直方图包含比颜色均值更丰富的颜色分布信息，其更适合用于艺术Mosaic拼贴的颜色校正，可实现图像灰度的重新排列，使指定图像色调拟合目标图像，从而获得子图像在原图中和谐融入的效果。鉴于此，笔者提出基于直方图匹配的艺术Mosaic并行拼贴算法，采用直方图匹配的方法选择最佳图像并进行颜色校正，使拼贴子图像之间过渡自然，获得高质量的艺术Mosaic拼贴视觉效果。另借鉴文献[16]，拼贴过程多处采用CUDA并行运算[17-18]，以期提高拼贴效率并实现交互式艺术Mosaic图像递归拼贴。

1 艺术Mosaic图像并行拼贴

提出的艺术Mosaic图像并行拼贴算法流程如图1。首先，对原图像基于四叉树结构进行分割，并分别计算各分割图像的RGB(red green blue，红绿蓝)直方图，同时根据分割布局生成原图像的分割索引表；其次，读取子图像库中的所有图像，且生成各自RGB直方图；然后，在GPU上基于直方图距离比较各分割图像与子图像的相似度，获取与各分割图像最相似的子图；最后，基于直方图匹配法对该子图像进行颜色校正以拟合分割图像，再根据分割索引表填充至原图像相应位置，生成艺术Mosaic拼贴图像。该拼贴算法中，原图像分割、直方图比较、颜色校正及子图像填充过程均使用CUDA并行计算。

1.1 分割索引表的并行生成

对图像进行艺术Mosaic拼贴，需分析整体图像分割布局并制作一张作为填充依据的分割索引表，以减少实时匹配计算量。首先，根据颜色分布对原图像基于四叉树多层分割，颜色变化缓慢区域用少量或单张子图像填充，细节丰富区域需多层细分并填充多张匹配子图像。拼贴细分过程中，根据用户定义最小分割尺寸对原图像统一分割，并将该分割结果作为第一层，即四叉树的叶子结点。然后，计算第一层每块图像颜色值，并从第二层开始逐层根据前一层的田字格计算当前层对应区域块的颜色均值，将其作为该田字格是否需合并的依据，从而得到原图像分割布局。如图2所示，其中图2(c)(d)分别为图2(a)(b)框出区域的第一、二层，图2(d)中每一块等同于图2(c)中4个相应位置的田字块。设第一层某田字格每块的颜色值为ci(i=1,2,3,4)，第二层对应格颜色值为C，判断颜色距离di=|C-ci|(i=1,2,3,4)是否大于指定阈值T，若di均小于T，则该块缺少颜色细节，将其合并为下一层的一整格，由此得到的分割结果如图2(b)。

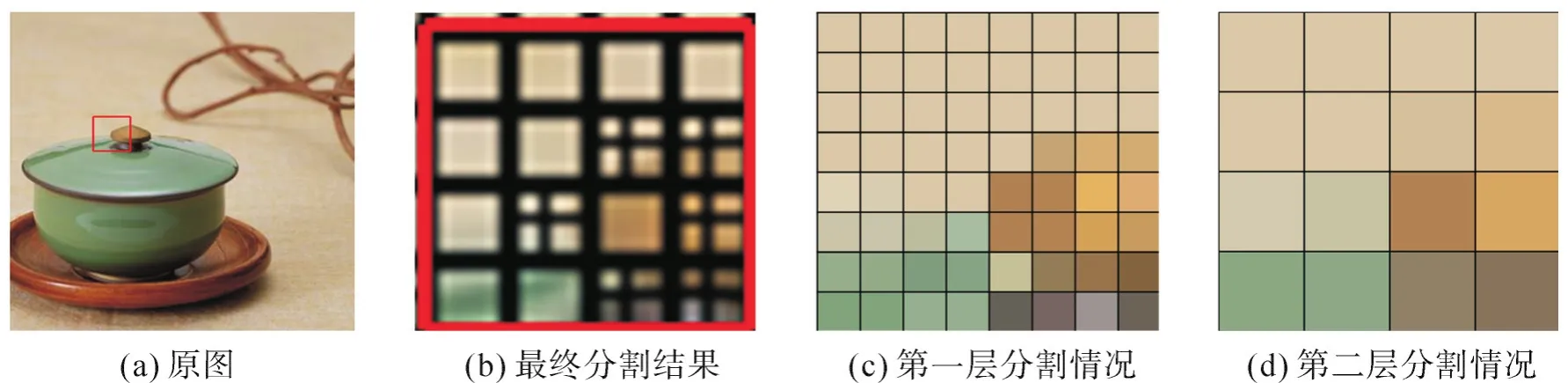
图2 图像分割Fig.2 Image segmentation

为便于后续子图像填充，制作一张二维分割索引表作为填充依据。该表中每个值都用二进制表示，其中二进制值(1111)2表示不可合并原图块，0表示可合并，整张索引表可表示原图像的分割情况。制作索引表步骤如下。

1)制作一张与第一层分割块数相同的表，并初始化为0，表示该格待合并为下一层。

2)若颜色距离di(i=1,2,3,4)至少有一项大于阈值T，则将下一层对应格设为(1111)2，表示该格颜色细节较丰富，需细分；若4项都小于阈值T，则设下一层对应格的值为0，表示可合并，如图3。

图3 分割索引表Fig.3 Index table of segmentation

3)根据前一层索引表所得二进制值，再次合并田字格得到下一层索引表，如图4。田字格中，左上角的格子位置由二进制值(0001)2表示，右上角由(0010)2表示，左下角由(0100)2表示，右下角由(1000)2表示。其中n表示第n层，n∈[1,N]，N为分割层数。下一层对应格的值为上一层四格中值为0的二进制求和，如式(1)。

图4 索引表合并Fig.4 Merging of index table

1.2 基于直方图的子图像并行匹配

通过计算直方图距离检索与分割图像最相似的子图像，较颜色均值法更能体现颜色分布，不易受极端颜色变化影响。

1.2.1 直方图的计算

为方便比较直方图，将子图像尺寸预先归一化为s×s（综合考虑到效率和子图像清晰度，文中选取子图像尺寸为512×512）。然后分别计算分割图像与各子图像的RGB直方图，并按序存入显存中，便于CUDA运算。

1.2.2直方图的比较

将每块分割图像与所有子图像进行RGB直方图对比，选取与分割块最相似的子图像，并将该子图像的编号填充至索引表中，从而得到子图像填充编号表，如图5，该表的生成规则如下。

1)设原图像总层数为N，当前层为n。当n≠N时，根据该层对应的分割索引表，若某格值为(1111)2，表示需细分，则根据式(2)分别计算该格对应四格直方图与所有子图像直方图的距离h。h值越小则图像越相似，选取最相似的图像编号填入子图像填充编号表相应位置，如图5。

其中：b为直方图计算设定的图像灰度区间数，较大的区间数表示灰度越细、匹配越好，但计算量也越大；分别表示分割图像在R(red，红)、G(green，绿)、B(blue，蓝)颜色通道第i个灰度区间中的像素个数；则分别表示子图像在R、G、B颜色通道第i个灰度区间中的像素个数。

2)若分割索引表中某格值为(1110)2，(1101)2等非零值，则该格对应田字格中存在已填充子图像，只需填充剩余未填充子图像，计算子图像填充编号方法同规则1)。

3)当n=N时，若该层索引表中某格值为0，则表示该位置需填充第N层分割大小的图像，子图像填充编号计算方法同规则1)。

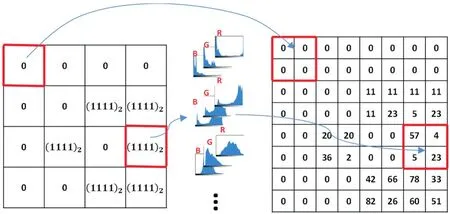
图5 子图像填充编号表Fig.5 Table of sub-image filling numbers

1.3 子图像的颜色校正与并行填充

直接填充匹配子图像会产生子图像间的明显边界，使原图像轮廓和细节过于模糊，因此需校正子图像颜色，使其色调尽可能拟合原图像。文中采用直方图匹配法进行颜色校正，将待填充子图像直方图调整至与目标图像块直方图基本一致，此时两幅图像色调也基本一致。直方图匹配的主要步骤如下：

1)计算子图像的累积直方图H；

2)计算分割图像的累积直方图M；

3)求H中每一个值在M中距离最小的位置j；

4)将子图像直方图通过索引j映射到相应分割后原图像的直方图。

相较于统计直方图，累积直方图不易受颜色变化与分布的影响，能更好地反映两幅图像之间的颜色差别。最后将经颜色校正的子图像填充到其相应位置。由于子图像均已调整为统一大小，填充时可根据目标填充大小均匀选取子图像像素填入。若子图像填充编号表中某格不为0，则选取子图像填入；反之则等待下一层填充，如图6。所有子图像填充完毕后，即为一幅完整的艺术Mosaic图像。

图6 子图像填充过程Fig.6 Process of sub-image filling

2 实验分析与应用扩展

通过实验对比分析基于直方图匹配法与颜色均值法的艺术Mosaic图像拼贴结果，并将单幅图像的单次艺术Mosaic拼贴扩展至递归式拼贴进行实验。实验中采用GeForce GTX 750 Ti显卡，RGB直方图的灰度区间数b设为10，子图像集数量为150张。

2.1 艺术Mosaic图像拼贴

图7，8分别为基于直方图匹配法与颜色均值法[12，17]的实验结果。其中原图像尺寸均为450×450，最小分割尺寸为9，拼贴层数设为2。

图7 基于直方图匹配的艺术Mosaic拼贴Fig.7 Artistic Mosaic collage based on histogram matching

图8 基于颜色均值法的艺术Mosaic拼贴Fig.8 Artistic Mosaic collage based on mean color method

比较图7，8可知：未进行颜色校正情况下，采用颜色均值法进行图像匹配的效果略优于直方图法，直方图法实验中为尽量减少计算时间，仅将直方图分为10个灰度区间，同一区间灰度值跨越度较大，因此直方图法的视觉差异较明显；颜色校正之后，基于直方图匹配的方法明显优于基于颜色均值的颜色校正，使用直方图匹配进行颜色校正更好地贴近原图像视觉效果，边界平滑过渡；颜色均值法的结果中，虽大部分颜色与原图像颜色接近，但普遍存在颜色突变现象，且子图像边界较明显，存在颗粒感，这主要源于直方图能体现颜色分布情况，可根据颜色分布对图像进行颜色调度；而颜色均值法对于颜色分布极端的情况不能很好地体现图像给人的印象色，颜色校正时也只能对所有像素整体加减灰度值，因此处于RGB通道极端灰度级区间的颜色易受颜色均值影响，视觉差异较大。此外，比较图7(b)(c)可见，通过离散化避免相同子图像相邻，有效减少了大面积区域块。

图9为未进行颜色校正时，用户设定不同分割层数的艺术Mosaic拼贴。原图像大小为512×512，最小分割尺寸为8。由图9可看出：分割层数设为多层时，对于颜色值相近区域，单张子图像即可良好表达该区域信息，细节部分则通过细分填充多张子图像展现。

图9 多层艺术Mosaic拼贴Fig.9 Artistic Mosaic collage with multiple layers

通过用户评测进一步验证本文算法的有效性。对50张原图像分别采用基于直方图和颜色均值的方法生成两组艺术Mosaic拼贴图片，同时加入原图像比较两种方法的拼贴效果。30名用户根据视觉效果选择心仪的拼贴效果图像。结果显示，平均每位用户选择基于直方图法的拼贴图像占总图像的比例是40.3/50=80.6%，由此可见用户更倾向于本文算法得到的结果。

选用20张相同尺寸原图像，统计基于CUDA的不同情况下算法的平均运行时间，结果见表1，2。表1为基于颜色均值且未颜色校正算法（简称A算法）的运行效率，表2为分割2层时不同算法的运行效率。其中：B表示基于颜色均值且使用颜色校正的算法；C表示基于直方图且未颜色校正的算法；D表示基于直方图且使用颜色校正的算法。由表1可见，A算法运行效率与原图像尺寸、子图像数量及用户所设层数密切相关。由表2可见：采用颜色校正比未颜色校正算法分别慢0.06，2 s；基于颜色均值比基于直方图算法快5～10 s，主要原因在于基于直方图算法中计算直方图较为耗时。艺术Mosaic拼贴过程具有较高的并行度，因此使用CUDA可加速本文算法，有效缩减处理时长。

表1 基于CUDA的A算法运行效率Tab.1 Efficiency of Algorithm Abased on CUDA

表2 二层拼贴各算法运行效率Tab.2 Efficiency of 2-layercollage with different algorithms

基于颜色均值算法的拼贴效率高于基于直方图算法，但对于子图像收集时的效率，其比基于直方图算法低很多。实验过程中，基于颜色均值算法收集子图像每次均耗时15 s左右，而基于直方图算法仅需2 s左右。因为基于颜色均值算法需在子图像收集时计算每张子图像每个通道的最大最小灰度值，用于后续颜色校正。因此，针对单张艺术Mosaic图像无需颜色校正的拼贴过程，基于颜色均值法较快；有颜色校正需求时，基于直方图法效率更高。

2.2 艺术Mosaic图像的递归式拼贴

借鉴文献[16]，对基于直方图的艺术Mosaic图像进行递归拼贴，即艺术Mosaic图像中子图像的放大与二次拼贴。此时子图像库不变，因此当原图像变化时，可直接使用显存中子图像及其直方图矩阵，节省大量计算时间。

图10(a)为已拼贴艺术Mosaic图像，当鼠标选中其中某一子图像后，该子图像平移至距离最近的窗口一角，如图10(b)，开始放大，如图10(c)。尽管图像放大会变模糊，但放大到预设阈值时，可将更清晰图像的像素并行填充至显示区域，此时图像会恢复至其未颜色校正状态，如图10(c)(d)。再次放大直到充满整个窗口，如图10(e)，对图像重新进行拼贴得到图10(f)，该过程可无限次执行。本文艺术Mosaic图像拼贴充分利用了显存中缓存的子图像库，提供交互式艺术Mosaic图像生成，满足用户以子图库任一张图作为原图递归生成新的艺术Mosaic图像。

图10 子图像放大再拼贴Fig.10 Enlargement and re-collage of sub-images

3 结 论

提出一种基于直方图匹配的艺术Mosaic图像拼贴算法，根据预设的分割层数及最小分割尺寸，基于四叉树对原图像进行分割。通过计算直方图距离检索与分割图像最相似的子图像，并采用直方图匹配法对子图像进行颜色校正和拼贴。相比于传统颜色均值法，基于直方图的子图像匹配和颜色校正生成的拼贴结果与原图像视觉上更相似，且平滑了子图像相接边缘，颜色细节更清晰，整体更和谐。使用CUDA对本文算法并行加速，可有效缩减拼贴处理时间，实现了递归式艺术Mosaic图像拼贴。

本文方法仍存在待改进之处，整体算法效率有待提高，虽可用于图像的交互式拼贴，但对于艺术Mosaic视频拼贴的实时性要求，依然存在较大差距。可从如下几个方面展开本文相关的下一步工作：增加拼贴子图像多样性，如方向角的改变、提取子图像显著性区域后拼贴[21]等；在图像分割与子图像匹配过程加入纹理、形状信息等。