机器人无标定手眼协调系统视觉跟踪

秦伟洋, 岳晓峰, 吴焕新, 张鹏飞

(长春工业大学 机电工程学院， 吉林 长春 130012)

0 引 言

手眼协调控制是机器人系统重要的控制手段。相比传统的在标定条件下使用的手眼协调系统，无标定视觉手眼协调系统具有更高的灵活性与适应性，是机器人伺服控制系统未来重要的发展方向和研究热点[1]。Herve[2]阐述了图像信息从图像空间映射变换到机器人任务空间的可操作性。Cooperstock J等[3]在手眼关系无标定的情况下，利用神经网络方法实现机器人的控制，进行了机器人的静态定位和抓取目标物体的实验。神经网络方法具有强大的函数拟合能力，能够比较准确地拟合机器人任务空间和图像空间之间的非线性关系，根据系统的动态特性建立控制率[4-5]，神经网络的缺点是必须进行大量的样本学习，相对来说，较为繁琐和复杂、计算量较大。苏剑波等利用ADRC方法来设计控制器[6-7]，其原理是将机器人手眼协调系统近似地看成一个简单的线性系统，将对该系统有影响的各种因素归为外部干扰，对其进行在线补偿，以此来实现系统的动态反馈。但这种方法由于系统响应初期误差较大，而且参数的选取大多是靠累积的经验，运动目标跟踪结果并不理想。Sutanto等通过研究实时估计图像雅可比矩阵来实现无标定手眼协调的方法[8-9]。

文中研究基于雅可比矩阵的无标定手眼协调系统视觉跟踪问题，提出一种改进的Kalman滤波算法对雅可比矩阵进行在线估计，并推导出相应的雅可比矩阵在线估计算法，在Matlab平台上进行仿真，验证了文中雅可比矩阵在线估计算法的可行性。

1 雅可比矩阵

假设f∈Rm为图像特征参数向量，r∈Rn为机械手在机器人工作空间中的位姿向量，m为图像特征空间维数，n为任务空间维数，则图像雅可比矩阵可以描述从机器人工作空间到图像特征空间的变换，其表达式如下：

(1)

其中

(2)

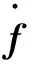
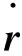
Ji(r)----图像雅可比矩阵，Ji(r)∈Rm×n。

此模型首先由Weiss[10]提出,它反映了机器人工作空间和图像特征空间的映射变换关系，又被称为特征敏感度矩阵[11-13]。

(3)

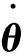
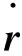
Jr(θ)----机器人雅可比矩阵,Jr(θ)∈Rn×p。

(4)

(5)

令

J=Ji(r)·Jr(θ)

则可以写为：

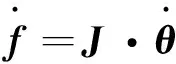
(6)

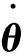
雅可比矩阵不是定常矩阵[14]，随着机器人的位姿改变，机器人运动空间和图像特征空间会发生相对变化，雅可比矩阵也会随之变化，因此雅可比矩阵具有时变的特点。所以，对雅可比矩阵进行实时估计是非常重要的。

2 图像雅可比矩阵的在线辨识

构造一个系统，将系统的状态设为待估计的雅可比矩阵参数，那么对系统的观测即可得到雅可比矩阵的估计值。根据图像雅可比矩阵的表达式，将其离散化，则有：

f(k+1)≈f(k)+J(r(k))·Δr(k)

(7)

设系统的观测矢量x是一个mn×1维矢量，定义如下：

(8)

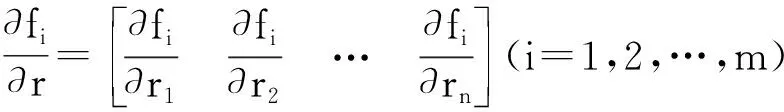
令图像雅可比矩阵的观测向量x(k)为系统状态，由机械手运动所引起的图像特征变化为系统输出，即y(k)=f(k+1)-f(k),得到如下状态方程：

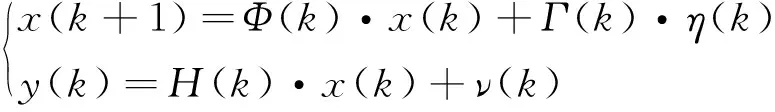
(9)

式中:η(k)，ν(k)----分别为状态噪声和图像观察噪声，假定为高斯白噪声。

根据系统特点和工程实际应用，建立简化的自适应Kalman滤波算法，将基于极大似然估计准则的R和Q矩阵的估计和调整问题转变成一个确定新息协方差矩阵Pv,以及对应的自适应调整参数αk的问题，其递推方程为：

状态预测：

(10)

观测噪声协方差阵：

(11)

系统噪声协方差阵：

(12)

增益矩阵：

(13)

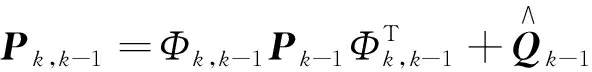
(14)

估计均方误差：

Pk=[I-KkHk]Pk,k-1

(15)

新息协方差矩阵：

(16)

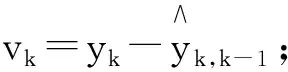
N----平滑窗口的宽度。

状态估计方程：

(17)

(18)

3 视觉控制器设计

(19)

式中:c1,c2----分别为PI控制器的比例与积分系数。

成像系统中，从世界坐标系变换到图像像素坐标系过程如下：

1)从世界坐标系到相机坐标系

(20)

其中,R为3×3的旋转矩阵，T为3×1的平移矩阵：

2)从相机坐标系变换到图像物理坐标系

(21)

式中:f----摄像机焦距。

3)从图像物理坐标系变换到图像像素坐标系

(22)

式中:fu,fv----分别为图像平面上X和Y轴方向上单位距离内的像素数;

u0,v0----分别为图像物理坐标系的中心坐标。

过程1)中的R，T一般被称为摄像机的外部参数。2)中的方程一般被称为摄像机的针孔模型。3)中的fu、fv、u0、v0以及2)中的f则是摄像机的内部参数。

4 仿 真

在Matlab平台上对手眼协调系统运动目标跟踪过程进行仿真，任务定义为：机器人末端执行器作二维平面运动，跟踪在工作平面上运动的点目标。使机器人末端执行期保持始终在目标点正上方。仿真参数设置如下：目标运动平面为机器人基坐标系的xoy平面，手抓运动平面高于xoy平面60 mm。手上摄像机相对于机器人末端坐标系设定为

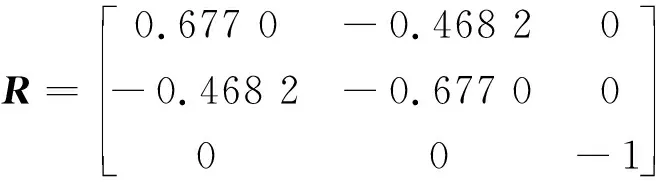
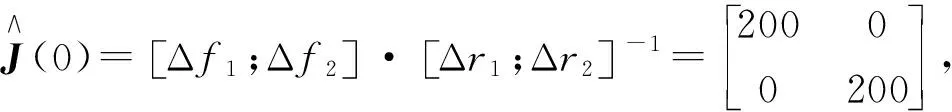
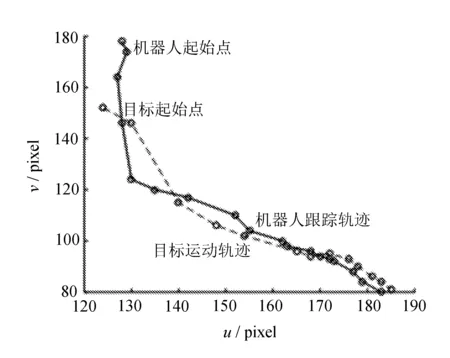
(a) 目标与机器人运动轨迹

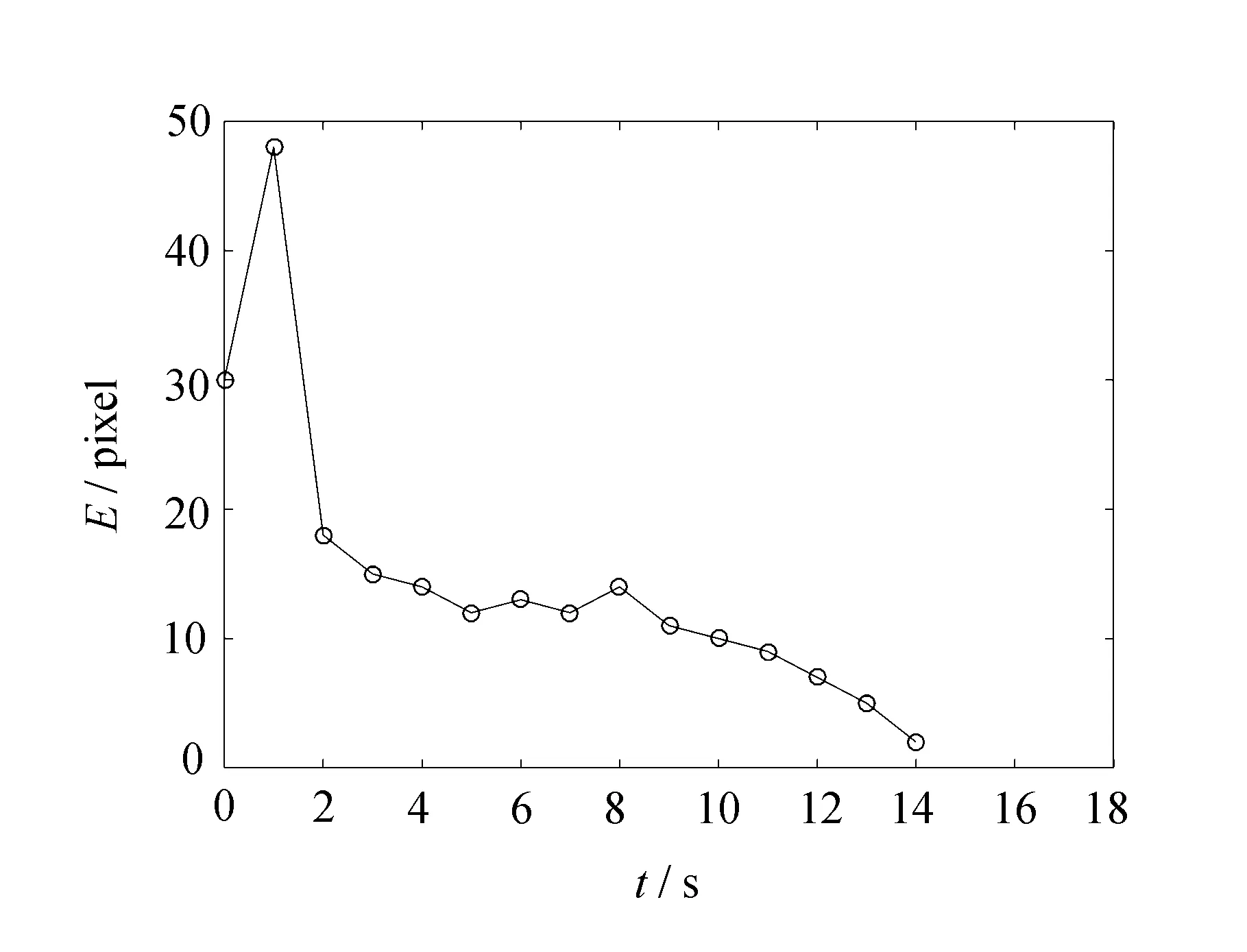
(b) 误差变化曲线

利用Kalman滤波算法对图像雅可比矩阵进行估计，对其进行相同条件的仿真，平面的仿真跟踪轨迹和跟踪误差变化如图2所示。

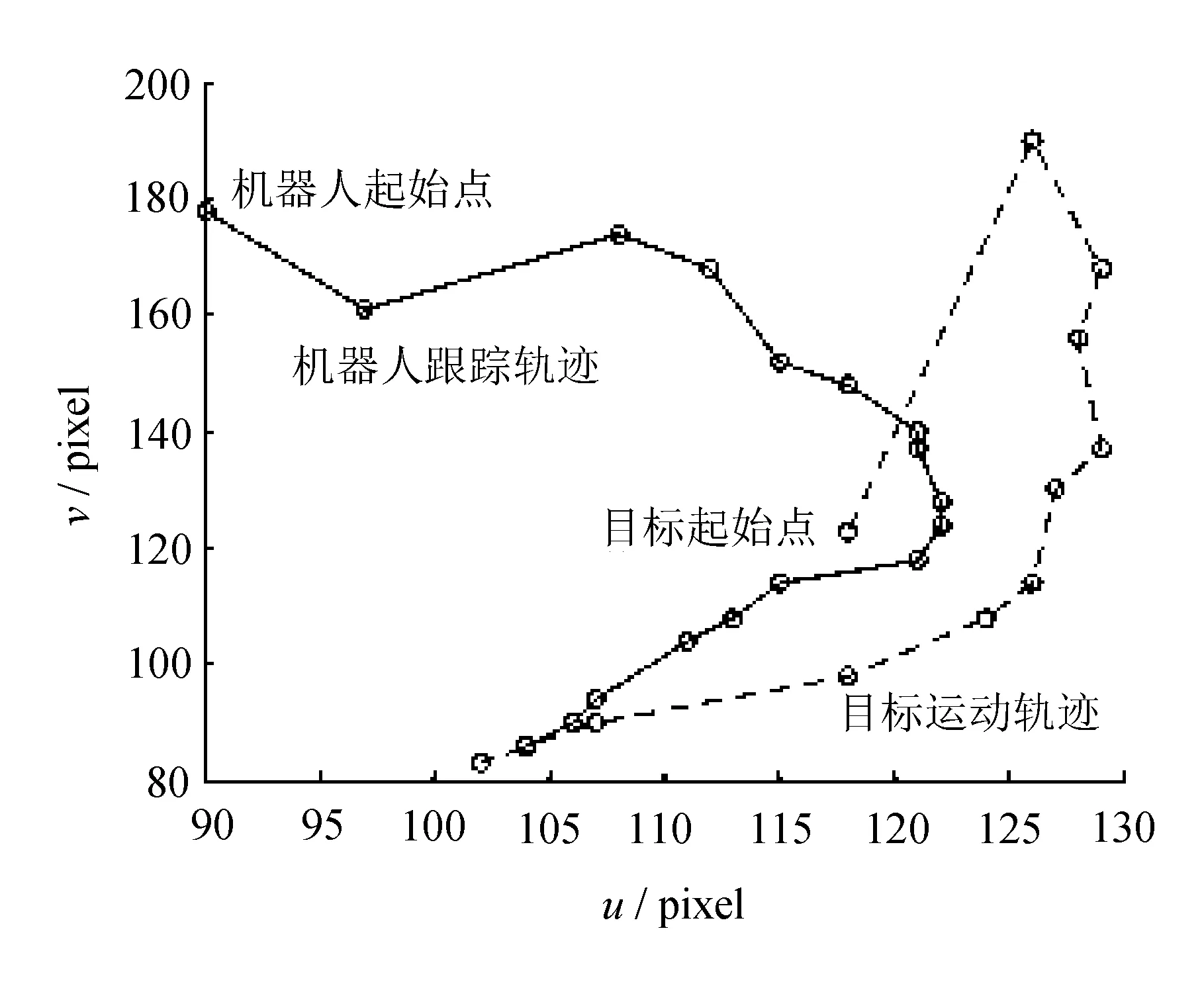
(a) 目标与机器人运动轨迹

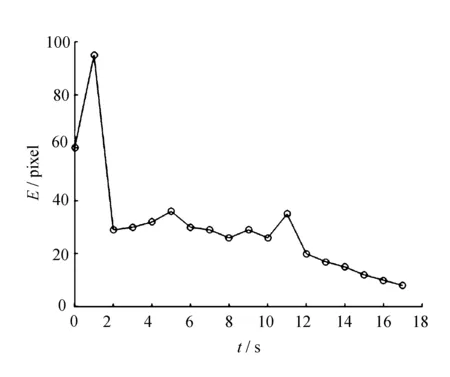
(b) 误差变化曲线

从图1(a)和图2(a)可以看出，比较利用Kalman滤波算法和文中提出的算法对图像雅可比矩阵进行在线辨识，文中提出的算法鲁棒性更好，机器人跟踪运动目标的准确率更高；从图1(b)和图2(b)可以看出，利用改进的Kalman滤波算法，跟踪误差较小且收敛速度较快。

5 结 语

分析了工业机器人手眼协调系统的原理，研究了世界坐标系、相机坐标系以及图像坐标系之间的变换关系，分析了图像雅可比矩阵的定义以及在线辨识算法，并提出了一种改进的Kalman滤波算法对其进行在线辨识，实现了机器人工作空间内跟踪运动目标，仿真结果验证了文中算法的有效性。

参考文献：

[1] Papanikolopoulos N P, Nelson B J, Khosla P K. Six degree-of-freedom hand/eye visual tracking with uncertain parameters[J]. Robotics & Automation IEEE Transactions on,1994,11(5):725-732.

[2] Herve J Y, Sharma R, Cucka P. Toward robust vision-based control: hand/eye coordination without calibration[C]// IEEE International Symposium on Intelligent Control. [S.l.]: IEEE,1991:457-462.

[3] Cooperstock J R, Milios E E. Self-supervised learning for docking and target reaching [J]. Robotics & Autonomous Systems,1993,11(3/4):243-260.

[4] 潘且鲁,苏剑波,席裕庚.基于神经网络的机器人手眼无标定平面视觉跟踪[J].自动化学报,2001,27(2):194-199.

[5] 谢冬梅,曲道奎,徐方.基于神经网络的机器人视觉伺服控制[J].微计算机信息,2006,22(4):4-6.

[6] 马红雨,苏剑波.基于耦合ADRC原理的机器人无标定手眼协调[J].机器人,2003,25(1):39-43.

[7] 刘晓丽.基于优化ADRC的无标定机器人手眼协调[D].西安:西安理工大学,2006.

[8] Sutanto H, Sharma R, Varma V. Image based autodocking without calibration[C]//IEEE International Conference on Robotics and Automation. [s.l.]: Proceedings. IEEE,1997,2:974-979.

[9] 钱江,苏剑波.基于图像雅可比矩阵的无标定二维运动跟踪[J].模式识别与人工智能,2003,16(3):257-262.

[10] Weiss L E, Sanderson A C, Neuman C P. Dynamic sensor-based control of robots with visual feedback [J]. IEEE Journal on Robotics & Automation,1987,7(5):404-417.

[11] Espiau B, Chaumette F, Rives P. A new approach to visual servoing in robotics[J]. IEEE Transactions on Robotics & Automation,1992,8(3):313-326.

[12] 钱江,苏剑波.图像雅可比矩阵的在线Kalman滤波估计[J].控制与决策,2003,18(1):77-80.

[13] 曾祥进,黄心汉,王敏.基于Broyden在线图像雅可比矩阵辨识的视觉伺服[J].华中科技大学学报:自然科学版,2008,36(9):17-20.

[14] 徐波，王金生，徐洲石.智能巡检机器人调度与路线规划能力[J].长春工业大学学报,2016,37(3):269-272.