探求一类最值问题的解题策略

程敬伟

（福建省惠安县第三中学）

题目 求函数（fx）=x+（0＜x≤1）的最小值。

本题函数的结构特征很容易让人产生应用均值不等式求解的思路,而且常会有以下解法：由于 0＜x≤1,所以 f（x）=x+然是个错解。在利用均值不等式求最值时“,一正二定三相等”这三个条件缺一不可，本题出现错误的原因在于没有验证不等式的等号是否成立。事实上，若x=,则x=±2,这在条件中定义域的制约下是无法取到的，因此，本题并不能直接简单地通过均值不等式来求解。

本文就上题为例探求其解题策略，以求达到解决型如（fx）=mx+（m，n都是大于0的常数）的一类函数在某个区间上的最值问题。

策略一：创设条件应用均值不等式求最值

∵0＜x≤（当且仅当x=1时，上式两个等号同时成立），∴函数（fx）的最小值为5。

评析：应用均值不等式是解决本题的直观想法，但必须要创造应用的条件。合理拆分项或配凑因式是常用的创设技巧，这需要在实践中多多体验、归纳、总结。

策略二：确定函数的单调性求最值

方式1：（利用定义确定函数的单调性）

设 0＜x1＜x2≤1，∴（fx2）-（fx1）＜0，即 （fx2）＜（fx1），∴ 函数 （fx）在x∈（0,1］上是减函数，∴当x=1时，函数的最小值为5。

方式2：（利用导数确定函数的单调性）

对函数 （fx）求导∴f′（x）＜0，∴ 函数 （fx）在x∈（0,1］上是减函数，∴ 当x=1时，函数 （fx）的最小值为5。

方式3：（利用单调函数的性质确定函数的单调性）

函数式可配方在x∈（0,1］上是增函数，∴函上都是减函数，∴函数函数，∴当x=1时，函数（fx）的最小值为5。

评析：创设应用均值不等式的条件有时技巧性较强，学生不易掌握，因此确定函数的单调性求最值是解决此类问题最主要的方法，本法有三种方式而应用导数是最为简捷方便的。

策略三：作出函数图象，应用数形结合思想求最值

函数 （fx）=x+的图象如下所示，则可知当0＜x≤1时，（fx）是减函数，∴当x=1时，函数的最小值为5。

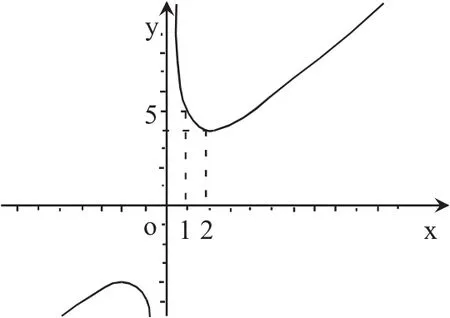
评析：函数图象形象地显示了函数的性质，为研究数量关系问题提供了“形”的直观性，它是探求解题途径、获得问题结果的重要工具，要重视这种数形结合解题的思想方法。

策略四：构建函数与方程，应用根的分布求最值

原函数式可变形为方程 x2-y·x+4=0，则方程在x∈（0，1］上有实数解。令 g（x）=x2-y·x+4，则 g（x）在（0，1］内有零点且故函数的最小值为5。

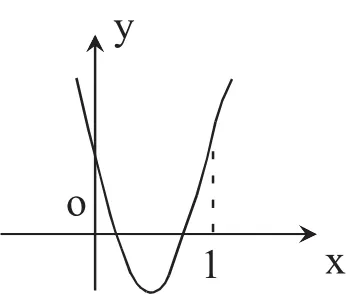
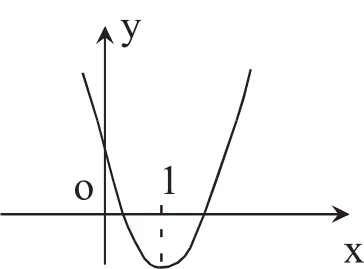
评析：函数与方程思想是解决最值问题的重要途径。本题通过构建二次方程，利用根的分布来处理，问题迎刃而解。

通过以上对本题不同的处理策略的探索，不仅让学生认识到把握问题本质的必要性，而且体会到从多角度、多方位思考问题的重要性，这不仅有利于培养学生良好的思维品质，激发了学生的学习兴趣，而且对于提高学生综合运用知识的能力大有裨益。