三棱锥外接球问题的模式探究
吴文姬
(福建师大二附中)
我们知道棱长分别为a、b、c的长方体,其外接球的直径就是长方体的体对角线,故而其外接球半径要是与长方体共顶点的三棱锥,我们都可以将之补成长方体,从而快速解题.那么由长方体顶点构成的三棱锥究竟有哪些类型呢?
模型1:(三棱互垂型)棱面垂直,底面是直角三角形

如图1,已知三棱锥P-ABC中,PA⊥平面ABC,且△ABC是直角三角形,PA=a,△ABC两直角边分别为b,c,则其外接球的半
例 1.在四面体SABC中,SA⊥平面 ABC,∠ABC=90°,SA=AC=2,AB=1,则其外接球的表面积为_________。
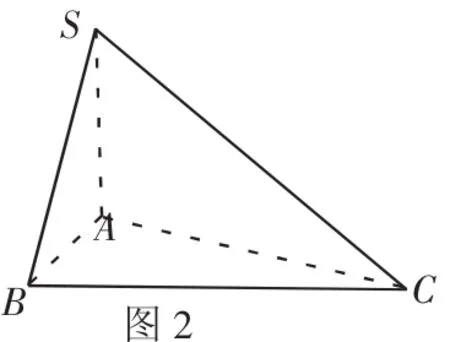

解析:如图2,这个三棱锥互垂的三棱分别为SA,AB,BC,故可以将其补成如图3的长方体,因此其外接球半径R=
模型2:(斜边公共型)一棱所对的两个角都是直角

如图 4,已知三棱锥 P-ABC 中,PC⊥AC,PB⊥AB,且 AP=1,
说明:AP中点O到A,B,C,P四点的距离相等,因此AP就是外接球的直径。需要特别说明的是AB与AC是否垂直并不影响这个结论。
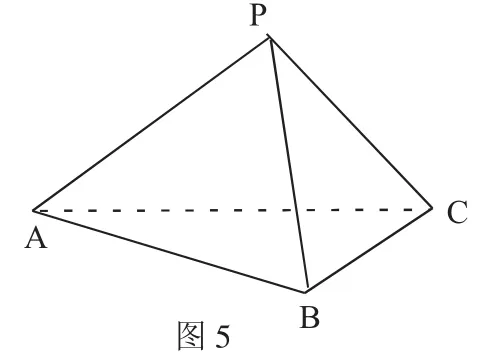
例2.在三棱锥P-ABC中∠ABC=,则三棱锥P-ABC外接球的表面积为( )。
A.4π B.π C.π D.16π
解析:如图5,在Rt△ABC中,由条件可知∠APC=,因此AC是两直角三角形的公共斜边,即外接球的直径。所以外接球半径R=2,故答案选D。
模型3:(对棱相等型)三对对棱分别相等

如图 6,已知三棱锥 P-ABC 中,PA=BC=l1,PB=AC=l2,且 PC=
例3.四面体中A-BCD中,AB=CD=2,AC=B
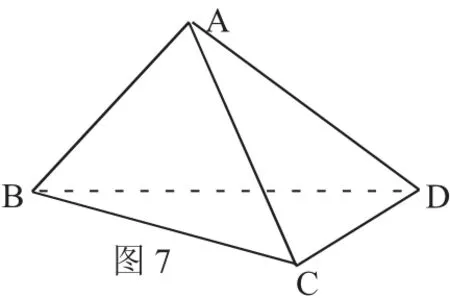
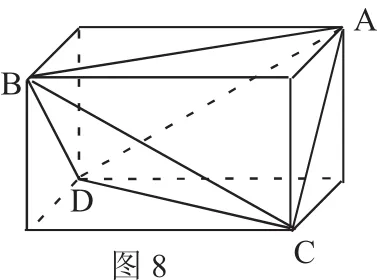
解析:如图7,三棱锥A-BCD因三对对棱相等,可以补成如图因此答案为6π。
这三个模型是以长方体为基础的模型中提炼出来,学生在解题时应认真分析图形的结构特征,熟练应用这三种模型,就能化繁为简,大大提高解题效率。
[1]赵舸.三棱锥的三视图问题解法扫描[J].高中生,2015(33).
[2]陶涛,刘艳清.用长方体模型解决棱锥外接球问题[J].高中生,2015(33).

