基于自适应的单形采样UKF组合导航算法

黄 平, 孙婷婷, 仝彦龙

(哈尔滨工程大学自动化学院, 黑龙江 哈尔滨 150001)

0 引 言

无迹卡尔曼滤波器(unscented Kalman filter,UKF)是近些年发展起来的一种非线性滤波[1-3]。它以无迹变换(unscented transform,UT)[4]为关键技术,以卡尔曼滤波为框架,通过确定性采样策略直接逼近状态的后验分布。UKF不仅提高了滤波精度,而且不必计算Jacobian矩阵[5-6],对系统模型没有要求,适用于任何线性和非线性模型。但UKF通常的问题是,采样点到中心点的距离会随着系统维数的增加而增大,产生采样的非局部效应问题[7-8];另外,传统的UKF采用对称采样策略[9],计算量大,无法应用到对实时性要求较高的系统中。针对UKF存在上述问题,很多学者进行了相应的改进算法研究[10-14]。但是上述文献中,作者只是在其中的一个方面改进UKF算法,并没有同时解决两个问题。

本文基于最小偏度单形采样[15]的比例UT变换,分析比例因子α的影响,提出了一种自适应的选取方法,并将改进后的算法应用在SINS/GPS紧组合导航系统中,通过Matlab仿真实验将其与传统的UKF进行对比,分析仿真结果。

1 自适应比例UKF算法

传统UKF算法采用对称采样策略,计算量较大,对于实时性要求较高的系统,如何降低计算量则成为首要的问题。对于一个n维分布的状态空间,对称采样需要2n+1个采样点,而最小偏度单形采样只需要n+2个采样点,虽然精度略有降低但计算量较小,综合考虑精度和计算量等因素,本文选用最小偏度单形采样。

1.1 最小偏度单形采样策略

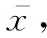
y=f(x)

(1)

首先选择

(2)

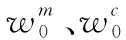
Sigma采样点一阶二阶权系数分别为

(3)

初始向量(对应于状态维数为j=1的情况)为

(4)

当输入维数为j=2,3,…,n时,其向量递推公式如下

(5)

根据式(5)生成的Sigma采样点为

(6)

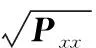
1.2 最小偏度单形采样的比例修正

UT变换虽然简单方便,但当系统维数较大时,会产生采样的非局部效应,导致估计精度下降,常用的解决办法是比例采样修正。修正算法为

(7)

(9)

(10)

(11)

式中,比例因子α取值范围一般为10-4≤α≤1,改变α的值,可以减小UT变换的非局部效应造成的影响。参数β用来描述x的先验分布信息,对于高斯分布的系统,β=2时最优。将此方法引入最小偏度单形采样算法,便可得到最小偏度单形采样的比例修正算法:

(12)

(14)

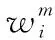
1.3 自适应比例因子的选取方法

在使用比例修正算法进行UT变换时,通常是给α取一个α∈[10-4,1]的固定值,虽然这有时也能得到满意的值,但这并不能使系统性能最优。如果能在递归运算时,每一步自适应地选取一个最合适的α参数,才能充分发挥α的性能。为此提出了一种自适应选取α的方法,如图1所示。

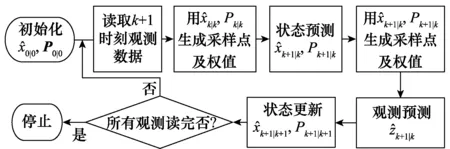
图1 UKF算法流程图Fig.1 UKF algorithm flowchart

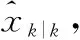
(15)

(16)

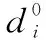
综合以上推导和分析,自适应选取比例因子α的具体步骤如下所示:

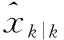
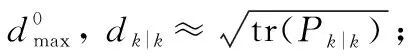
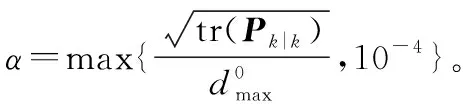
在每次UT变换的过程中,用自适应比例因子α对采样策略进行修正,就得到自适应比例无迹卡尔曼滤波(adaptive scaled unscented Kalman filter, ASUKF) 算法。

2 SINS/GPS紧组合系统的模型

2.1 SINS/GPS紧组合导航系统的状态方程

2.1.1 SINS误差方程

(1) 平台误差角方程

(17)

式中,φt=[φE,φN,φU]T;陀螺漂移εt=[εE,εN,εU]T=Tεb,T为姿态矩阵。

(2) 速度误差方程

(18)

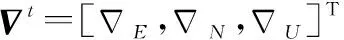
(3) 位置误差方程

(19)

式中,λ,L,H为当地经度、纬度和高度;RN和RM别是运载体在地球上某一点的卯酉圈的曲率半径和子午圈的曲率半径。

(4) 惯性仪表误差方程

通常取陀螺漂移为

εb=εc+εr+ωg

(20)

式中,ωg为陀螺仪的随机漂移,假定其为高斯白噪声;εr表示陀螺仪的一阶马氏过程,假定其为当前时刻的陀螺漂移;εc表示陀螺仪的常值漂移。

加速度计的测量误差包含零偏和随机噪声,可表示为

(21)

式中,Ta表示相关时间;ωa表示加速度计的随机漂移。

系统误差状态方程的一般表达式为

(22)

式中

XI=[φEφNφUδυEδυNδυUδλδLδh

2.1.2 GPS误差状态方程

GPS的误差状态,在紧组合系统中,通常取时钟误差等效的距离误差δtu与时钟频率误差等效的速度误差δtru。

(23)

式中

XG(t)=[δtu,δtru]T,WG(t)=[ωtu,-ωtru]T

将SINS误差状态方程与GPS误差方程合并,则得到紧组合系统的状态方程。

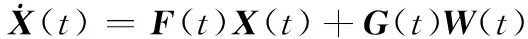
(24)

其中

X(t)=[XI(t),XG(t)]T,W(t)=[WI(t),WG(t)]T

2.2 SINS/GPS紧组合导航系统的量测方程

在GPS/SINS紧组合导航系统中,选择SINS和GPS两者伪距之差和伪距率之差作为组合导航系统的观测量。

2.2.1 伪距误差量测方程

Zρ(t)=Hρ(t)X(t)+Vρ(t)

(25)

2.2.2 伪距率误差量测方程

(26)

将伪距量测方程式与伪距率量测方程式合并,则组合成组合导航系统的量测方程,组合系统的量测方程可表达为

(27)

也即

Z=HX+V

(28)

由于滤波器采用离散系统滤波方程进行滤波计算,还需要将上述方程离散化处理。

2.3 ASUKF滤波

(1) 滤波初值选取

设置初始比例因子α并计算Sigma样本点和相应的权值,再根据第1.3节介绍的方法更新比例因子α=αk+1|k。

(2) 时间更新

将Sigma采样点通过状态函数求取系统的一步状态模型值，即

(29)

预测k+1时刻的模型值，即

(30)

(31)

(32)

估计系统的量测值:

(33)

(3) 量测更新:

计算自协方差矩阵Pzz(k/k-1)和互协方差矩阵Pxz(k/k-1):

(34)

(35)

计算增益阵:

(36)

校正状态的预测值:

(37)

更新系统的协方差:

(38)

3 仿真分析

3.1 仿真参数设置

仿真所使用的轨迹是利用Matlab产生的机载运动,系统导航信息的输出频率为100 Hz,GPS的输出频率为10 Hz,组合导航系统的数据输出频率与SINS系统同步。设陀螺仪常值漂移0.1°/h,白噪声均方差0.01°/h;加速度计常值零偏1×10-4g,白噪声均方差5×10-5g;GPS伪距白噪声10 m,伪距率白噪声0.5 m/s。飞机产生的航迹如图2所示,机体在东、北、天3个方向上的位置、速度和姿态如图3所示。

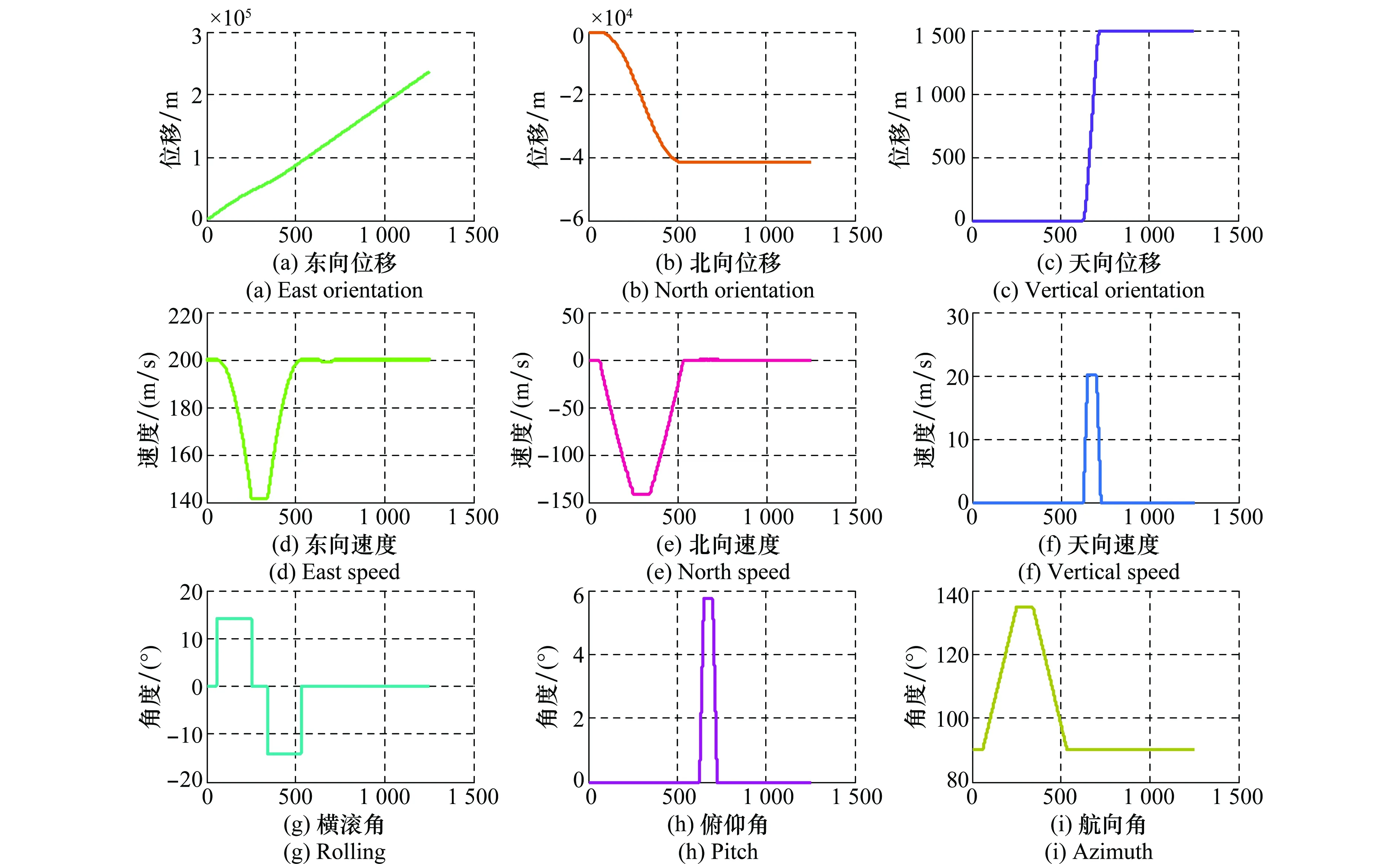
图3 载体各方向运动Fig.3 Each direction of motion of the carrier

3.2 仿真结果

分别采用对称采样UKF、单形采样UKF(记为SUKF)和采用单形采样策略的ASUKF算法对SINS/GPS导航系统的紧组合模型进行Matlab仿真,并对实验结果进行对比分析,如图4和图5所示。

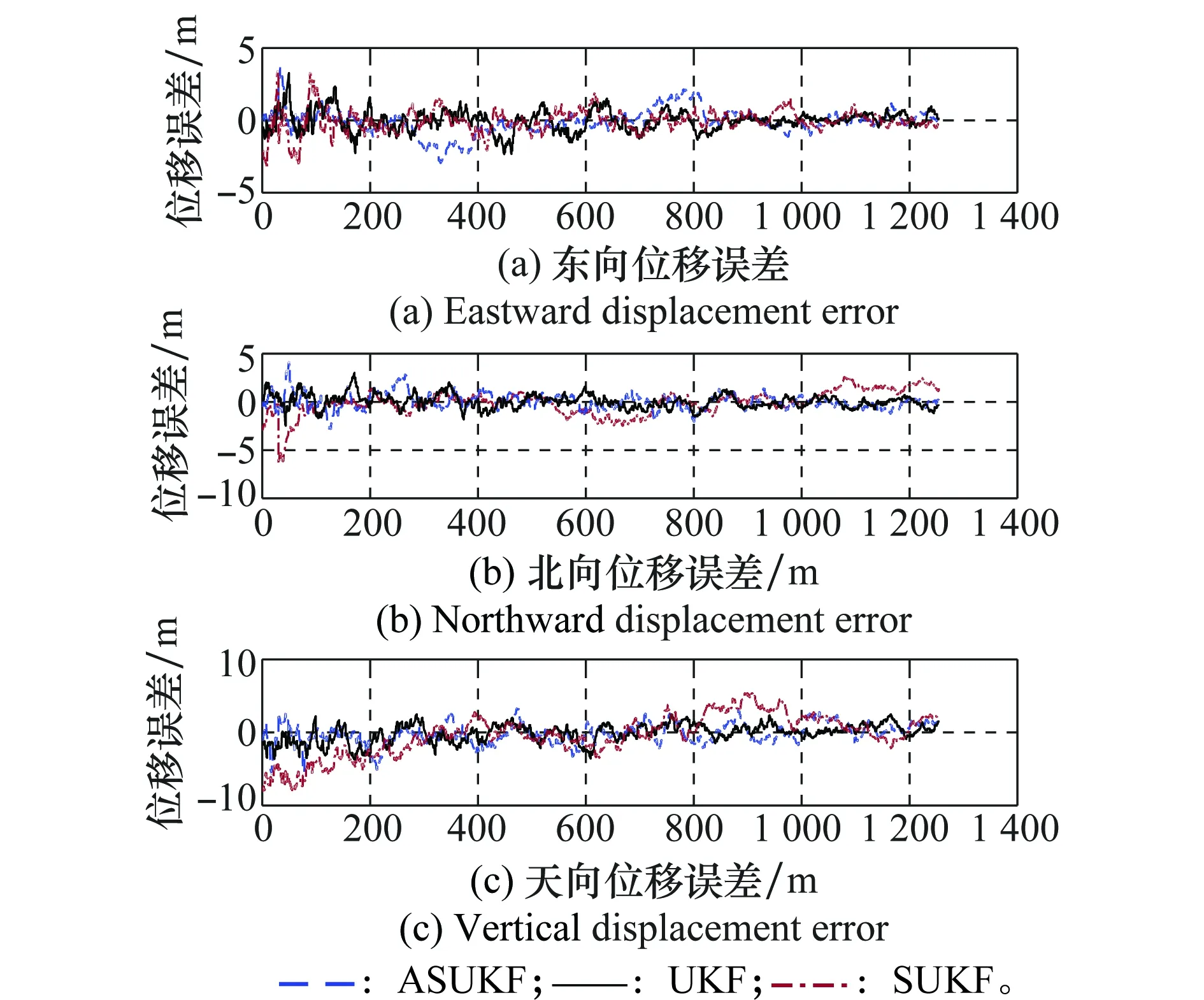
图4 定位误差Fig.4 Positioning error

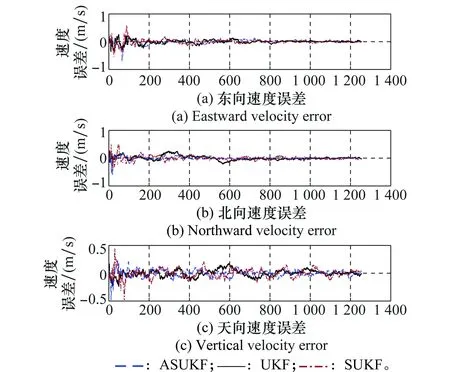
图5 速度误差Fig.5 Velocity error

重复进行50次MC仿真实验,并计算3种UKF算法各类误差信息的RMSE,统计这3种UKF算法的平均运行时间,结果如表1所示。

表1 紧组合3种UKF算法仿真效果对比

3.3 仿真结果分析

由图4和图5的误差曲线图及表1的仿真效果统计信息可得:曲线最终均收敛在零值附近,且这3种UKF算法估计输出的速度误差均值都小于0.1 m/s,定位误差都不大于3 m,说明这3种算法都能取得不错的滤波效果。对比这3种滤波算法的误差曲线可以得出,固定比例数的SUKF滤波精度比采用对称采样的UKF滤波精度稍差,但用时比对称采样UKF少了大概有30%。ASUKF算法虽然在UT变换的过程中,计算量较固定比例参数的单形采样UT变换策略只是略微增大,大概增大了5%,但其精度却有很大的提高,尤其是其速度精度提高了将近20%,位置精度也有10%多的提升。而ASUKF滤波与常规的对称采样UKF滤波相比,在估计精度大体相同的情况下,使计算量却减小了大约25%。综合来看,ASUKF算法精度较高,计算量也较小,与理论分析基本一致,综合效果最好。

4 结 论

文中针对UKF做出了一些改进,采用最小偏度单形采样策略和比例参数自适应改进UKF算法。既降低了系统的计算量,提高了精度,也减弱了UT变换的非局部效应,但仍有一些问题尚未解决:

(1) 本文中比例参数α的取值范围是根据经验确定的,并未对其进行推导验证,也不一定就是最优值,还需要对比例参数α的自适应选取问题做更深入的研究。

(2) 在做Matlab仿真时可以发现:与对称UKF相比,系统维数越高,自适应比例参数UKF算法计算量优势越明显,但精度有些下降,如何选择合适的维数还需再做深入的研究。

参考文献：

[1] STRAKA O, DUN J, JIND K, et al. Unscented Kalman filter with advanced adaptation of scaling parameter[J]. Automatica, 2014, 50(10): 2657-2664.

[2] ANASTASIA D, ANDREOPOULOS Y. Throughput distortion computation of generic matrix multiplication: toward a computation channel for digital signal processing systems[J]. IEEE Trans.on Signal Processing, 2012, 60(4): 2024-2037.

[3] JINWHAN K, VADDI S S, MENON P K, et al. Comparison between nonlinear filtering techniques for spiraling ballistic missile state estimation[J]. IEEE Trans.on Aerospace and Electronic Systems, 2012, 48(1): 313-328.

[4] 刘庆元, 郝立良, 黄书捷,等. 改进的UKF在 GPS/INS 组合导航中的应用[J]. 测绘科学技术学报, 2014, 31(5): 450-453.

LIU Q Y, HAO L L, HUANG S J, et al. The application of improved UKF in GPS/INS integrated navigation[J]. Journal of Surveying and Mapping Science and Technology, 2014, 31(5): 450-453.

[5] 管军, 易文俊, 常思江, 等. 基于UKF的北斗/SINS 组合导航系统研究[J]. 弹道学报, 2015, 27(1): 1-6.

GUAN J, YI W J, CHANG S J, et al. Research on the navigation system of Beidou/SINS base on UKF[J]. Journal of ballistic, 2015, 27(1): 1-6.

[6] ZHOU W D, CAI J A, SUN L, et al. Time-space difference based GPS/SINS ultra-tight integrated navigation method[J]. Measuremnet, 2014,58: 87-92.

[7] BISHT S S, SINGH M P. An adaptive unscented Kalman filter for tracking sudden stiffness changes[J]. Mechanical Systems and Signal Processing, 2014, 49(1/2): 181-195.

[8] ZHU Z L, SHAN Y D, YI Y, et al. INS/GNS integrated method based on innovation orthogonality adaptive Kalman filter[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 66-70.

[9] HU G G, GAO S S, ZHONG Y M. A derivative UKF for tightly coupled INS/GPS integrated navigation[J]. ISA Transactions, 2015, 56: 135-144.

[10] CAFFERY L J, SMITH A C. Investigating the quality of video consultations performed using fourth generation (4G) mobile telecommunications[J]. Journal of Telemedicine & Telecare, 2015, 21(6):348.

[11] MOHAMMAD T S, POURIA S, MOSTAFA Z. Extended and unscented Kalman filters for parameter estimation of an autonomous underwater vehicle[J].Ocean Engineering,2014,91(15):329-339.

[12] HUANG J, YAN B. Federated filter based on dynamic information allocation with unscented Kalman filter[C]∥Proc.of the International Conference on Electrical, Computer Engineering and Electronics, 2015: 911-916.

[13] 冯鹏程,胡高歌,高社生.基于新息正交原理的抗差UKF及其在INS/GPS组合导航中的应用[J].测控技术,2015,34(10):92-95.

FENG P C, HU G G, GAO S S. Robust UKF based on the principle of new interest orthogonality and its application in INS/GPS integrated navigation[J]. Measurement and Control Technology, 2015, 34(10): 92-95.

[14] GUPTA M, BEHERA L, SUBRAMANIAN V K, et al. A robust visual human detection approach with UKF-based motion tracking for a mobile robot[J]. IEEE Systems Journal, 2015, 9(4): 1363-1375.

[15] 李晓旭, 戴彬, 曹洁. 基于多特征融合的改进UPF目标跟踪算法[J]. 上海交通大学学报, 2014, 48(10): 1474-1478.

LI X X, DAI B, CAO J. Improved UPF target tracking algorithm based on multi feature fusion[J]. Journal of Shanghai Jiaotong University, 2014, 48(10): 1474-1478.