采用ESO补偿的再入飞行器姿态预测控制方法

王 涛, 张洪波, 汤国建

(1. 国防科技大学航天科学与工程学院, 湖南 长沙 410073; 2. 中国人民解放军32032部队, 北京 100094)

0 引 言

大升阻比再入飞行器是这些年的研究热点,它能借助气动力进行大范围机动,实现定点着陆。可应用于空间作战、天地运输等任务。但由于其自身结构特点和高超声速的飞行速度,姿态系统呈现较强的非线性和耦合性,对控制器设计要求较高。

PID控制方法是最早的再入飞行器姿态控制方法,已在航天飞机上得到成功验证。为了提高控制系统的性能,一些先进的控制算法逐渐被引进来。如线性化控制方法[1]、鲁棒控制方法[2]、最优控制[3]、滑模变结构控制方法[4]、模糊控制方法[5-6]、自抗扰控制算法[7]、预测控制算法[8]等。其中,预测控制方法在解决高超声速飞行器快时变控制问题中表现出了良好的适用性。文献[8]基于动态逆方法设计了预测控制律,将输入量约束和状态量约束映射为虚拟控制量的约束,然后对虚拟控制量寻优。文献[9]采用泰勒级数展开的近似方法将非线性系统线性化,进一步得到解析的预测控制方法。文献[10]提出了基于模糊系统的非线性预测控制方法,采用模糊系统逼近非线性运动方程,保证了预测控制方法的精度。文献[11]提出了一种预测滑模控制方法,结合了滑模控制算法和预测控制算法的优点。

为了提高系统的鲁棒性,干扰观测器被引到姿态控制律中。文献[12]采用一种干扰观测器实时观测参数不确定性,抑制了滑模控制中的抖振现象。文献[13]和文献[5]分别将扩张滑模观测器和扩张状态观测器(extended states observer,ESO)应用到滑模控制律和模糊控制律中,达到了良好的效果。文献[14-16]将干扰观测器引入到预测控制律中,分别采用支持向量回归方法[14]、滑模干扰观测器[15]、和非线性观测器[16]对外界扰动进行在线估计,改善了预测控制律的性能。

本文针对再入飞行器姿态运动提出了一种基于ESO的预测控制方法。首先将姿态系统分成姿态角回路和姿态角速率回路,降低了系统的阶数。然后针对两个回路分别设计控制器。采用动态逆方法将运动方程线性化,并基于此推导了解析的最优预测控制律。为了提高控制器的精度和鲁棒性,采用ESO对模型误差和不确定干扰进行估计,并在预测控制律中进行补偿。最后通过六自由度仿真测试,验证了控制方法的性能。

1 运动模型

已知飞行器的攻角为α,侧滑角为β,倾侧角为σ,令x=[α,β,σ]T,姿态角速度ω=[ωx,ωy,ωz]T,则姿态运动模型为

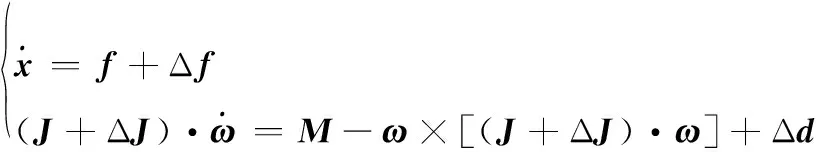
(1)

式中,Δf为有界模型误差项,包含地球自转和质心运动对姿态运动的作用项,参见文献[5];ΔJ为转动惯量误差;Δd为扰动力矩,二者也是有界的。f、J、M表达式为

式中,J为惯量矩阵;MAero,0为稳态气动力矩;Mc为操纵力矩,包含气动舵偏角产生的力矩MAero,δ和RCS产生的力矩MRCS;M的变化范围可根据飞行器的状态变量、舵偏角的变化范围以及RCS的性能进行计算,M∈[Mmin,Mmax]。

2 控制律设计

根据飞行器姿态运动的特性,将姿态控制系统分为姿态角回路(外环)和姿态角速率回路(内环),对两个回路分别进行控制器设计,如图1所示。[α0,β0,σ0]T为制导指令,外环控制器通过调节ωc跟踪制导指令,内环控制器通过调节Mc跟踪ωc。本文采用预测控制方法,为了得到解析的控制律,首先采用动态逆方法将运动系统线性化。

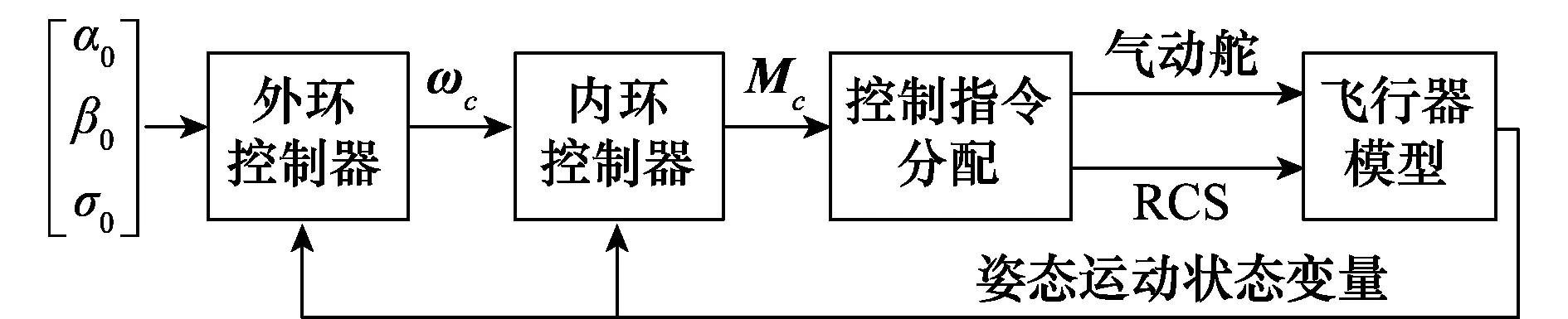
图1 飞行器控制系统结构图Fig.1 Control system of entry vehicle

2.1 外环控制律

外环运动方程为方程(1)的第一式,考虑到地球自转和平移运动对姿态影响较小,将Δf视为建模误差,同时构建中间变量v=[vx,vy,vz]T,动态逆控制律为

(2)

将以上控制律代入方程(1)的第一式,得到以v为控制量的线性状态方程

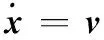
(3)

将状态方程(3)离散化,假定α、β、σ为系统输出量

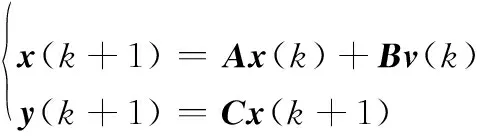
(4)

其中

式中,Ts为采样周期,假设控制周期为p个动力学积分步长,第p步的状态为

(5)

将p个时刻的状态组合起来

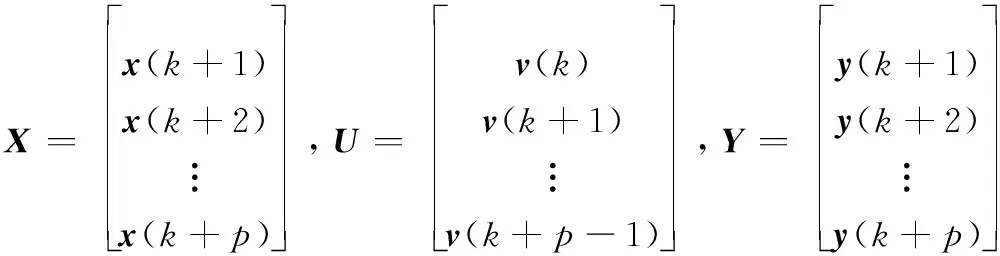
(6)

新的状态方程为

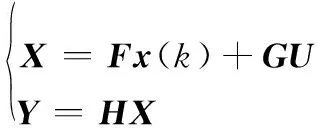
(7)

式中

(8)

取优化指标

Jmin=[Y-Yref]TQ[Y-Yref]+UTRU

(9)

式中,Yref为标称值,由制导系统给出。对J求导

2HGQ[HFx(k)+HGU-Yref]+2RU

(10)

为使性能指标取得最优,令∂Jmin/∂U=0,得到

U=((HG)TQHG+R)-1HGQ(Yref-HFx(k))

(11)

式中,Q和R为加权矩阵。其表达式为

式中,n和m分别为状态变量和控制变量的维数,n=m=3,如果令矩阵中的权值相等,则存在q1=q2=…=qn×p=q,r1=r2=…=rm×p=r,通过调节常数q和r改善控制器的性能。

预测控制律建立在动态逆线性化模型的基础上,而动态逆方法必须以精确的动力学模型为前提,因此对动力学模型中的不确定项Δf进行估计,不断修正动力学模型,保证控制算法的精确性。采用扩张状态观测器ESO[17]对Δf进行估计,ESO如下:

(12)

式中,z1(k)为第k步x的估计值;z2(k)为第k步Δf的估计值;e为估计值与输出值的误差;h为ESO的步长;u(k)为第k步的控制量;f0为状态方程(1)中的确定部分,此处令f0=0;b为控制量的系数矩阵,表达式为

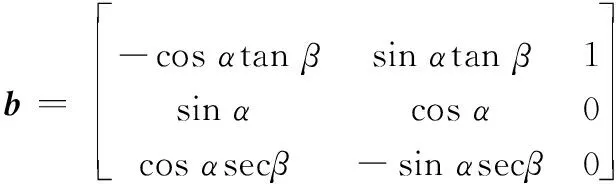
(13)

方程(12)中fal的表达式如下:

(14)

式中,β01、β02、δ为ESO的参数,参见文献[17]。

2.2 内环控制律

内环运动方程为方程(1)的第二式,将内环运动方程进行整理得

MAero,0+Mc-ω×(J·ω)+Δg

(15)

式中,Δg为误差总和。构造中间变量w=[wx,wy,wz]T,动态逆控制律为

Mc=(J·w-Δg)+ω×(J·ω)-MAero,0

(16)

将方程(16)代入到方程(15)中,得到线性化状态方程

(17)

按照对外环系统的处理方式,将方程(17)离散化,并设计预测控制律

U2=((HG)TQHG+R)-1HGQ(Yref,2-HFω(k))

(18)

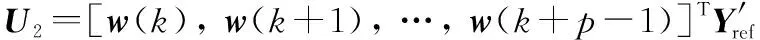
如果考虑控制力矩约束,将得不到解析的控制律表达式,此时可将其转化为二次规划问题,然后采用有效集求解,从而得到最优控制指令。实时求解二次规划问题会增加计算量,对控制约束有一种简易的处理方法,首先求解无约束的控制律,如果控制力矩超出范围,则取边界值,这种方法不能保证控制律是最优的。另一方面,增大优化指标中的R矩阵,也可有效地减小控制力矩的幅值。

然后,采用ESO对方程(16)中的不确定因素Δg进行估计,从而得到姿态运动的控制力矩。

在再入飞行器的姿态控制中,需要将控制力矩分配给各个控制机构。由于论文研究的重点在于控制算法,控制指令分配方法参考文献[18],此处不再详述。控制力矩与控制机构的关系为

(19)

式中,q为飞行动压;S为飞行器参考面积;b为参考长度;Cm(α,Ma,δ)为气动系数,与攻角α、马赫数Ma以及舵偏角δ有关;RRCS为RCS安装位置;FRCS为RCS的推力矢量。

3 稳定性分析

采用动态逆方法处理运动方程(1)后,姿态内外回路的闭环方程相似,只需证明一个回路的稳定性即可。以外回路为例,闭环系统为

(20)

式中,v为预测控制器的间接控制量;z2为ESO对Δf的估计值。对于有界的不确定因素,ESO的估计误差也是有界的[17],即|z2-Δf|≤ε,ε为接近零的常数。因此,要证明方程(20)稳定,只需证明方程(3)稳定即可。

对于方程(3)的离散系统,已知预测步数为p,在控制的作用下,判断第p步的状态x(k+p)是否稳定。为了不失一般性,一个预测控制周期内,控制步数设置为l(l≤p)。相关矩阵为

(21)

式中,I为3维单位方阵,q、r为正数;将方程(21)、方程(11)代入到外环运动方程(4)中,则闭环运动方程的系统矩阵为

A*=I-G(GTQG+R)-1GQF

(22)

为了便于求解A*,考虑到处理后的系统各状态变量之间已经解耦,因此只对单状态变量进行分析。

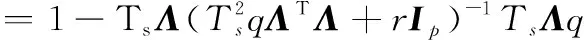
(23)

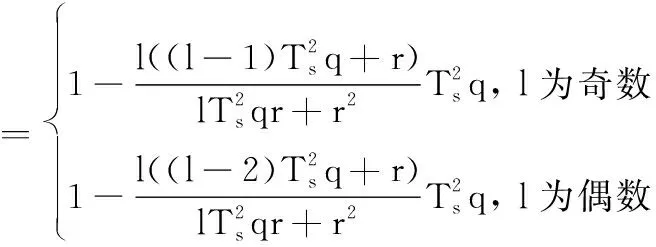
(24)

如果系统是稳定的,对于任意正定对称矩阵S,必然存在正定对称矩阵P,满足离散李雅普诺夫方程

A*TPA*-P+S=0

(25)

将方程(23)代入方程(25)得到

(26)

因为q、r、Ts为正数,由方程(24)可知A*<1。如果S正定,则P也正定,所以外环回路是稳定的。同理,采用此方法也可证明内环回路是稳定的。

4 仿真校验

对本文中姿态控制方法进行仿真实验。假设飞行器的质量为2 700 kg,惯量矩阵为

以飞行器再入过程中的某一局部状态为仿真场景,飞行高度60 km,飞行速度4 000 m/s。初始攻角为39°,初始倾侧角和侧滑角都为零,三者的制导指令分别设置为40°、2°和0°。扰动惯量ΔJ=0.1J,扰动力矩Δd=sin(t)·[50,100,100]TN·m。

离散采样周期为Ts=0.05 s。预测控制律中,设置p=2,控制器参数Q=I,R=0.02I。状态观测器ESO参数β01=200,β02=500,δ为5倍的ESO步长。仿真结果如图2和图3所示。

图2给出了控制器对制导指令的跟踪效果,从左到右依次是攻角、倾侧角、侧滑角的变化,实线为制导指令,虚线为控制器的跟踪曲线。在预测控制器的作用下,初始偏差被消除。尽管系统中存在干扰力矩,但干扰被控制器抑制,姿态角的稳态曲线在微小的范围波动。图3给出了飞行器的控制力矩曲线,从左到右依次对应于滚转、偏航、俯仰通道。控制力矩呈现明显的波动,这抵消了扰动力矩的影响,保证了良好的控制效果。其中,滚转力矩的稳态值不为零,这是因为飞行器的质心与几何中心有微小的偏移量,飞行器大攻角飞行时的升力比较大,产生了不利的滚转力矩,要使飞行器姿态稳定,必须控制滚转舵补偿该力矩。

图2 固定点的姿态角跟踪结果Fig.2 Tracking curves of attitude angles for a local state

图3 固定点的控制力矩Fig.3 Control moments for a local state

进一步,为了充分测试预测控制律的性能,在整个再入过程中施加姿态控制。再入段参数如表1、表2所示。以表1中的数据为再入起始点,表2中的数据为终端约束,制导算法采用文献[19],对飞行器进行六自由度仿真分析。

表1 再入初始点数据

表2 再入终点数据

飞行器的控制机构包含RCS和气动舵。在高层大气中,由于大气密度稀薄,采用RCS进行姿态控制。随着高度的降低,大气密度逐渐稠密,气动舵的控制能力逐渐增强,从而代替RCS成为姿控的主要执行机构,具体控制分配算法参考文献[18]。仿真结果如图4～图6所示。

图4给出了整个再入过程的控制结果。从左到右依次是攻角、倾侧角、侧滑角的变化。即使在倾侧角翻转时,控制器也展示出较好的跟踪效果。从侧滑角的控制曲线可以看出,前半部分为RCS控制,曲线较为震荡,后半部分为气动舵控制,曲线较为平滑,曲线跳跃处对应于倾侧角的翻转位置,反映出横向运动和侧向运动有一定的耦合作用。图5和图6给出了控制力矩曲线和控制机构响应,从左到右依次对应于滚转、偏航、俯仰通道。图6和图7分别给出了气动舵响应曲线和RCS开关机响应曲线。再入初始阶段,采用RCS进行控制,控制力矩出现抖动,从而导致图4中姿态角的震荡。当进入气动舵控制阶段时,控制力矩变得平缓。当制导指令剧烈变化时,控制力矩急剧增大。

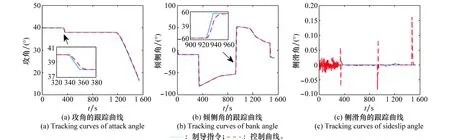
图4 再入过程中的姿态角跟踪结果Fig.4 Tracking curves of attitude angles for entry process

图5 再入过程中的控制力矩Fig.5 Control moments for entry process

图6 再入过程中气动舵响应曲线Fig. 6 Rudder response for entry process

图7 再入过程中RCS响应曲线Fig. 7 RCS response for entry process

5 结 论

针对再入飞行器的姿态运动,本文提出了一种基于ESO的最优预测控制律。得到结论如下:

(1) 采用动态逆方法将系统线性化,得到了最优预测控制律的解析表达式;

(2) 采用ESO对模型误差和扰动因素进行估计,保证了控制精度和鲁棒性;

(3) 仿真中升力产生了不利的滚转力矩,然而却得到了有效地补偿,这体现了预测控制律的优势,合理利用了各个通道的控制能力;

(4) 横向通道和侧向通道耦合性较强,倾侧角翻转导致侧滑角跳变,要抑制这种跳变需要增大控制器参数r。

参考文献：

[1] JOHNASON E N, CALISE A J. Limited authority adaptive flight control for reusable launch vehicles[J]. AIAA Journal of Guidance, Control and Dynamics, 2003, 26(6): 906-913.

[2] XIN M, BALAKRISHNAN S N. Nonlinear H∞missile longitudinal autopilot design with θ-D method[J]. IEEE Trans.on Aerospace and Electronic Systems, 2008, 44(1): 41-56.

[3] CIMEN T. Survey of state-dependent Riccati equation in nonlinear optimal feedback control synthesis[J]. Journal of Guidance, Control and Dynamic, 2012, 35(4): 1025-1047.

[4] GENG J, SHENG Y Z, LIU X D. Finite-time sliding mode attitude control for a reentry vehicle with blended aerodynamic surfaces and a reaction control system[J]. Chinese Journal of Aeronautics, 2014, 27(4): 964-976.

[5] 胡超芳, 刘运兵. 基于ESO 的高超声速飞行器模糊自适应姿态控制[J]. 航天控制, 2015, 33(3): 45-51.

HU C F, LIU Y B. Fuzzy adaptive attitude control based on ESO for hypersonic vehicles[J]. Aerospace Control, 2015, 33(3): 45-51.

[6] SONG B, MA G F, LI C J. Robust fuzzy controller design for a rigid spacecraft attitude regulation system[C]∥Proc.of the International Symposium on Systems and Control in Aerospace and Astronautics, 2006.

[7] PU Z Q, YUAN R Y, TAN X M, et al. An integrated approach to hypersonic entry attitude control[J]. International Journal of Automation and Computing, 2014, 11(1): 39-50.

[8] RECASENS J J, CHU Q P, MULDER J A. Combined feedback linearization and constrained model predictive control for entry flight[J]. Journal of Guidance, Control, and Dynamics, 2006, 29 (2): 427-434.

[9] WANG P, TANG G J, LIU L H, et al. Nonlinear hierarchy-structured predictive control design for a generic hypersonic vehicle[J]. Science China Technological Sciences, 2013, 56(8): 2025-2036.

[10] 方炜, 姜长生. 基于自适应模糊系统的空天飞行器非线性预测控制[J]. 航空学报, 2008, 29(4): 988-994.

FANG W, JIANG C S. Nonlinear predictive control of an aerospace vehicle based on adaptive fuzzy systems[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(4): 988-994.

[11] CHEN X L, TANG G J, WANG P, et al. Predictive silding mode control for attitude tracking of hypersonic vehicle using fuzzy disturbance observer[J]. Mathematical Problems in Engineering, 2015, 2015: 1-13.

[12] 王芳, 宗群, 田栢苓, 等. 再入飞行器带有干扰观测器的有限时间控制[J]. 控制理论与应用, 2016, 33(11): 1527-1534.

WANG F, ZONG Q, TIAN B L, et al. Finite time control design for re-entry hypersonic vehicle with disturbance observer[J]. Control Theory & Applications, 2016, 33(11): 1527-1534.

[13] SAGLIANO M, MOOJI E, THEIL S. Adaptive disturbance-based high-order sliding-mode control for hypersonic-entry vehicles[J].Journal of Guidance,Control,and Dynamics, 2017,40(1):1-16.

[14] CHENG L, JIANG C S, PU M. Online-SVR-compensated nonlinear generalized predictive control for hypersonic vehicles[J]. Science China Information Sciences, 2011, 54 (3): 551-562.

[15] 高海燕, 蔡远利. 高超声速飞行器的滑模预测控制方法[J]. 西安交通大学学报, 2014, 48(1): 67-72.

GAO H Y, CAI Y L. Sliding mode predictive control for hypersonic vehicle[J]. Journal of Xi’an Jiaotong University, 2014, 48(1): 67-72.

[16] 孙光, 朱如意, 王征. 基于干扰观测器的飞行器再入姿态广义预测控制[J]. 航天控制, 2016, 34(4): 10-15.

SUN G, ZHU R Y, WANG Z. Generalized predictive control of vehicle re-entry attitude based on disturbance observer[J]. Aerospace Control, 2016, 34(4): 10-15.

[17] 韩京清. 自抗扰控制技术[M]. 北京: 国防工业出版社, 2008.

HAN J Q. Active disturbance rejection control technology[M]. Beijing: National Defense Technology Press, 2008.

[18] 房元鹏. 可重复使用航天器再入段复合控制方法研究[J]. 飞行力学, 2008, 26(1): 60-63.

FANG Y P. Research on composite control method for reusable launch vehicle[J]. Flight Dynamics, 2008, 26(1):60-63.

[19] 王涛, 张洪波, 朱如意, 等. 考虑阻力加速度的再入预测-校正制导算法[J]. 宇航学报, 2017, 38(2): 143-151.

WANG T, ZHANG H B, ZHU R Y, et al. Predictor-corrector reentry guidance based on drag acceleration[J].Journal of Astronautics, 2017, 38(2): 143-151.