3-DOF并联微夹取器的运动学建模

，，

(南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京 210016)

0 引言

近几十年来，随着微纳米技术的快速发展，研究对象的不断细微化，微操作技术受到人们越来越多的关注[1-3]。为了实现对微小物体的抓取、移动等操作，微操作机器人的末端执行器需要2个手指的协调作用，即微夹取器。目前，绝大多数的微夹取器均是以基于镊子夹取物体的操作原理而设计的，它具有结构简单、操作方便、控制精度高的特点[4-7]。但是，由于2根手指之间只有1个自由度，限制了微夹取器的操作能力。而采用基于筷子操作原理的方式对细胞进行抓取、翻转是更加灵活的操作方式。日本东京大学的Tanikawa[8]和Ramadan[9]设计了一种由压电陶瓷管驱动的基于筷子操作原理的微夹取器，其操作空间为几百微米，定位精度小于0.1 μm。虽然该微夹取器成功抓取了微米级的球形物体，但是它的结构复杂，体积也较大，进而造成加工成本高等问题。

在此，提出了一种由直线超声电机[10-11]驱动的基于筷子操作原理的三自由度并联微夹取器，其结构紧凑且简单。利用空间坐标转换和矢量链法建立了其运动学模型，求解了微夹取器输入与输出的运动学关系。通过实验测量验证了该运动学模型的准确性，并对出现的误差进行了分析，最后运用该微夹取器成功夹取了虾卵细胞。

1 微夹取器结构

基于筷子操作原理的微夹取器是微操作机器人设计的发展方向。本文所设计的微夹取器采用并联结构，它包括手臂、驱动部件、柔性铰链、圆盘、固定手指、活动手指和底座，如图1所示。手臂为圆柱体结构，固定在底座上，是微夹取器的主体支撑结构。为方便将驱动部件安装在手臂上，在手臂的圆柱形表面切割出3个凹槽，3部驱动元件均匀安装在手臂的中轴线周围，两两相差120°。驱动部件包括直线超声电机、滑块和直线导轨，其中导轨与手臂的中轴线平行。3个万向柔性铰链的一端固定在导轨上，另一端固定在圆盘上。固定手指安装在手臂上，指尖穿过圆盘上的中心孔，不产生任何运动。活动手指安装在圆盘上，与手臂中轴线成一夹角，指根固定在圆盘上的位置与其中一个柔性铰链的底端面关于圆盘对称。

直线超声电机驱动导轨移动，导轨带动圆盘转动，而圆盘的转动实现活动手指的运动，从而实现活动手指和固定手指之间的相对运动，并用于对微小物体进行抓取和调整位姿的操作。3个导轨的位移是相互独立的，它驱动圆盘产生1个自由度的平动和2个自由度的转动，因此，活动手指也有3个自由度的运动，表现在手指尖端点在x,y,z3个方向的移动。

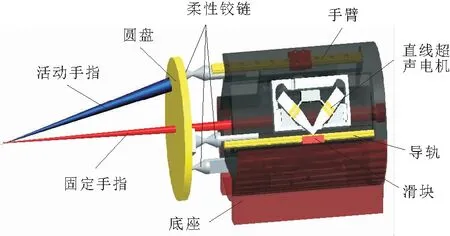
图1 微夹取器的结构示意

2 运动学建模及分析

该微夹取器采用的是万向柔性铰链，其在受力时可产生弯曲变形从而使得运动平台能够转动。圆盘在实际操作中发生的转动角度极其微小，因而柔性铰链的弯曲变形也极其微小[9]，因此为了简化模型，得到简单的且更直观的运动学模型，将各向同性的万向柔性铰链视作球铰。

2.1 运动学模型描述

由于固定手指没有运动，因此只针对活动手指来建立模型。微夹取器的数学模型如图2所示。全局坐标系{O}建立在手臂的底面圆心处，z轴沿着手臂中轴线，正方向指向圆盘，x轴指向其中一条运动链，根据直角坐标系右手法则，y轴方向也就确定了。圆盘视为一个以C为圆点、R为半径的活动平台。3条相同且平行的运动链通过与底面垂直的滑动副di(由直线超声电机驱动)来连接底面和活动平台，i=1,2,3代表运动链的顺序。运动链和活动平台之间由球铰Pi连接，其在活动平台上的分布如图3所示。

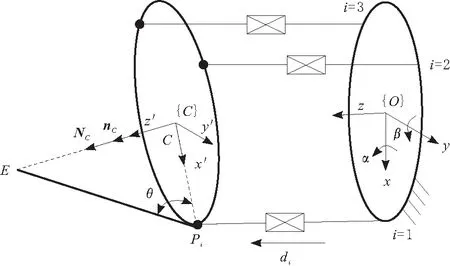
图2 微夹取器的数学模型

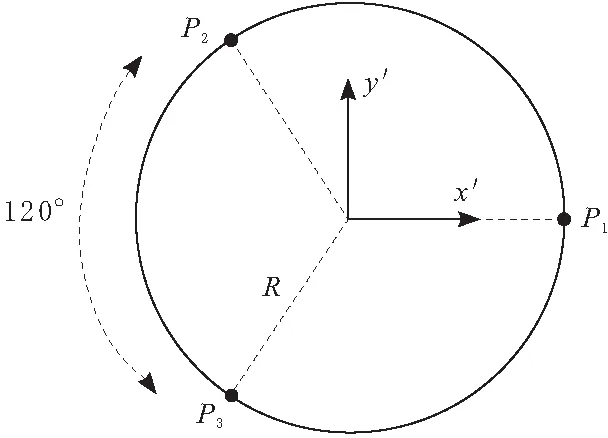
图3 铰链在活动平台上的分布

手指的一端固定在与球铰P1相连的活动平台上，与活动平台之间的角度为θ，另一端点定义为点E，即微夹取器的操作末端。在活动平台的圆心C处建立局部坐标系{C}，其法向量为NC,单位法向量为nC。微夹取器的广义输出坐标定义为xE=[xEyEzE]T，其中，xE，yE，zE表示操作末端在全局坐标系中的位置。球铰在坐标系{O}中的位置为xPi=[xPiyPizPi]T。初始状态下，活动平台没有发生转动，即手指的末端点E与活动平台中心点C之间的连线垂直于圆柱形底面。

由于活动平台在z轴方向没有转动，所以活动平台相对于全局坐标系的转动，可以用1个3×3的空间坐标变换矩阵来表示。根据刚体有限转动欧拉定理可知，坐标系{O}和坐标系{C}之间的空间坐标变换矩阵为：

RXY′(α,β)=RY′(β)·RX(α)=

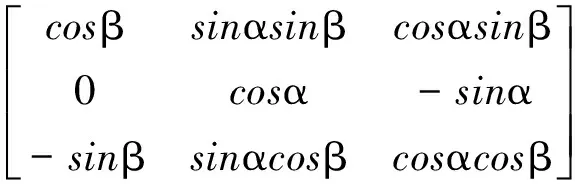
(1)

RX，RY′为坐标轴各次转动后所对应的方向余弦矩阵；角α，β分别为活动平台绕x轴和y轴的转动角度。根据微夹取器的数学模型，利用矢量链法可得操作末端点E在全局坐标系中的坐标为：

(2)

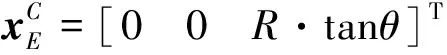
(3)

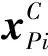
(4)

球铰在坐标系{O}中z轴的坐标即直线滑动副在z轴的坐标，对于直线滑动副，也就是输入变量di有:di=zPi。因此，通过式(4)即可得到该微夹取器的运动学模型。

2.2 各运动链输入与输出的位移关系

式(4)中含有未知变量α和β，为了通过输入变量di来计算活动平台的转角α和β，利用活动平台的法向量与转角之间的关系来获得。如图4所示，假设

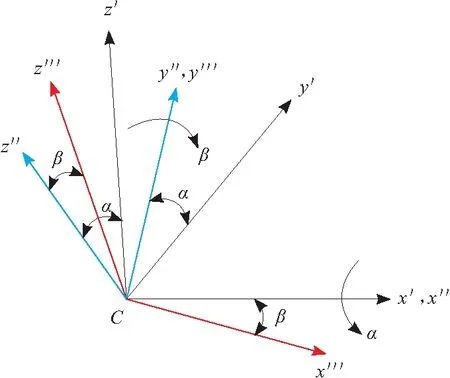
图4 先α后β旋转坐标系

活动平台的起始坐标系{C}首先绕着x′轴转动了角度α，此时x′轴与平面y′y″z′z″是垂直的。然后，转动后所形成的新的坐标系{Cx″y″z″}绕着y″轴转动了角度β，那么x′轴，z″轴，z‴轴是在一个平面内的，因此可得：β=π/2-∠x′Cz‴。

同理，当活动平台的起始坐标系{C}首先绕着y′轴转动角度β，然后新坐标系{Cx″y″z″}再绕x″转动α，可得：α=∠y′Cz‴-π/2。

为了得到∠x′Cz‴和∠y′Cz‴的表达式，可利用活动平台的单位法向量来求解。由di=zPi，可得由输入变量di表示的铰链Pi在全局坐标系中的坐标位置为：

(5)

进而可分别求得活动平台的法向量和单位法向量分别为：

(6)

[cos∠x′Cz‴ cos∠y′Cz‴ cos∠z′Cz‴]

(7)

|NC|=

i，j，k代表全局坐标系{O}中的单位法向量。

联合上述各式，角α，β即可由di求出，分别为：

(8)

(9)

根据式(4)所描述的运动学模型，微夹取器的输出位移xE可由输入位移di表达出来。如果只考虑操作末端的位移变化量ΔxE随输入的位移变化量Δdi之间关系，可得到3条运动链上输入与输出之间的位移关系，分别为：

(10)

(11)

(12)

3 微夹取器的实验研究

构建如图5所示的实验系统，来测试所研制的微夹取器的工作性能，开展抓取微小物体的实验。为了实时测量直线超声电机的输出位移，即微夹取器的输入位移，将位移分辨率为0.5 μm的光栅尺安装在3条导轨的尾部。利用高精度电子显微镜系统的显示器能实时监测手指末端的运动情况，即能测量微夹取器的输出位移。

图5 微夹取器的实验系统

3.1 运动学关系验证

微夹取器的圆盘半径为R=52 mm。令活动手指与圆盘之间的夹角θ为60°，这样的角度既能保证2根手指方便地对物体进行抓取操作，又能使得整体机构紧凑，不会因为手指过长而造成微夹取器的体积太大。

分别驱动图2中3条运动链上的超声电机导轨运动，选取导轨的移动位移量为0.1～1 mm之间的10个点，在显微镜下测量活动手指尖端在x轴、y轴和z轴上的移动位移量。通过多次实验测量取平均值后，与利用MATLAB软件计算出的运动学模型理论结果作对比，如图6～图8所示。图6～图8中的曲线代表模型计算结果，圆圈、三角形和星点分别代表手指尖端在x轴，y轴和z轴上的实验测量值。

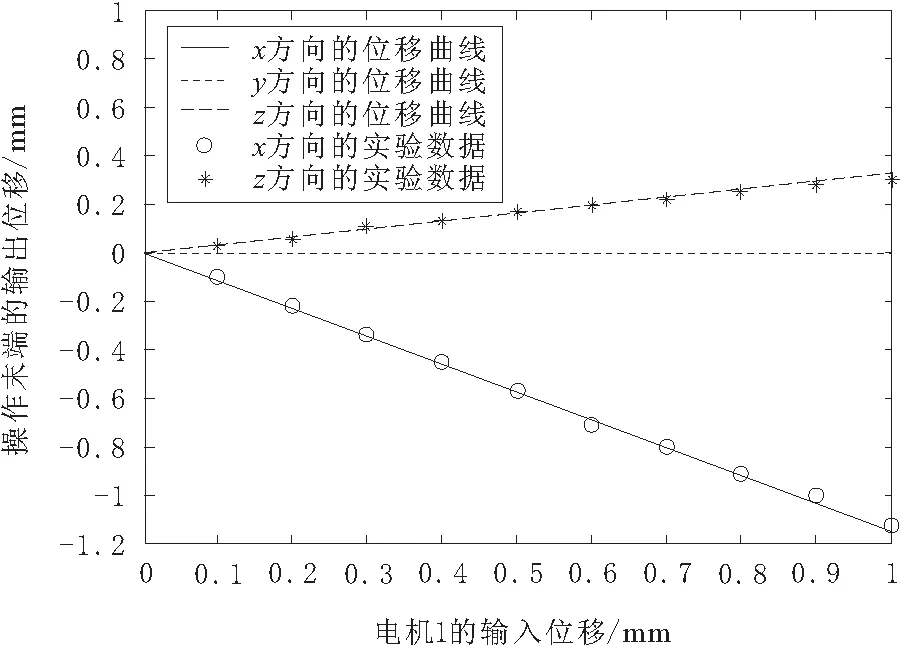
图6 运动链1的理论与实验对比

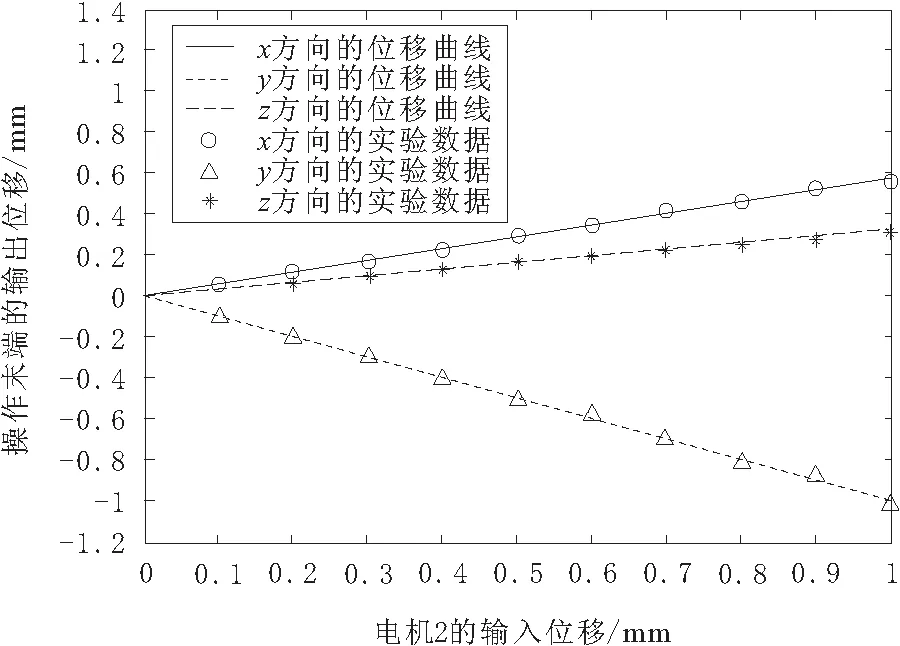
图7 运动链2的理论与实验对比

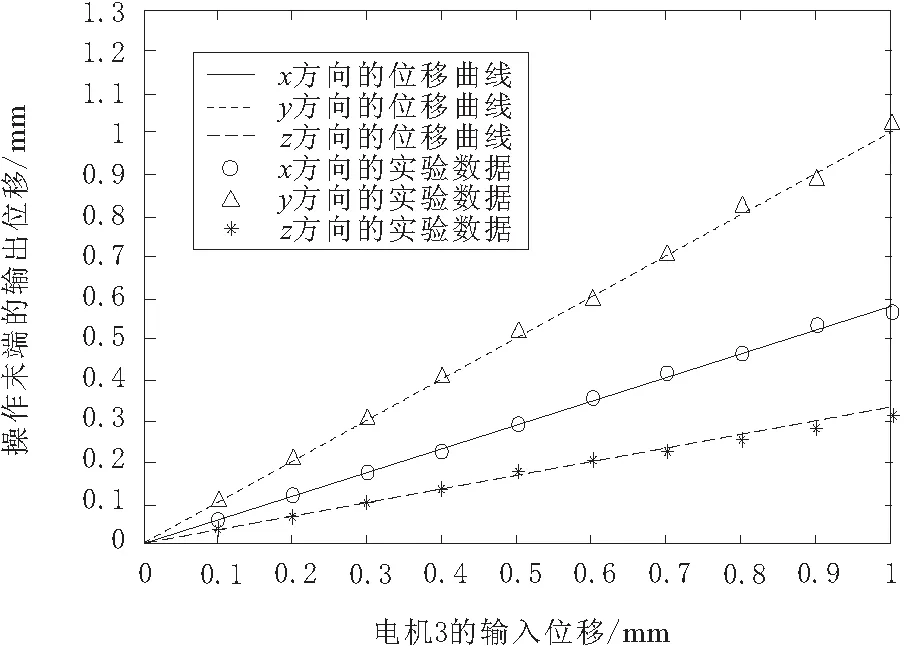
图8 运动链3的理论与实验对比

3.2 误差分析

由图6～图8可知，3条运动链在x，y，z轴上的实验测量值与理论计算结果都基本吻合，只有部分数值有超过20 μm的误差，而且误差大的测量点都分布在电机驱动到1 mm的位置附近，其原因主要有：

a.所建立的运动学模型没有考虑柔性铰链的弯曲变形而造成的在x-y平面上的位移，因此柔性铰链的弯曲变形量越大，实验测得的实际值与模型结果相差越大。

b.当电机的输入位移在1 mm左右时，此时柔性铰链的变形恢复力很大，使得操作末端存在机械漂移现象。

c.直线超声电机具有响应快、瞬时冲击力大的特点，因此会引起操作末端的微幅振动。

3.3 虾卵细胞的夹取实验

为了探究该微夹取器的夹取性能，开展了对微小物体的夹取实验研究。显微镜下抓取直径约为250 μm虾卵细胞的具体过程如图9所示。首先，根据被抓取物体的大小调整2根手指尖端之间的距离，如图9a所示。然后，使固定手指末端缓慢靠近细胞，最终触碰到虾卵细胞的一侧，如图9b所示，以便活动手指的夹取工作。接着，驱动第1条运动链上的超声电机，使活动手指末端靠近细胞，第2条和第3条运动链的电机用来保证2根手指对细胞位置的姿态调整和平衡，如图9c所示。最后，通过调节3个电机的运动，当细胞有一定的变形量时，则表示已经抓取成功，如图9d所示。单人便可完成抓取的整个过程，而且对操作人员的要求不高，使用起来比较方便。

图9 虾卵细胞的夹取过程

4 结束语

提出了一种由直线超声电机驱动的基于筷子操作原理的3-DOF并联微夹取器。为简化模型，将万向柔性铰链简化为球铰，利用空间坐标转换和矢量链法建立了其运动学模型，求解了微夹取器各运动链输入与输出的位移关系。构建了微夹取器的实验系统，通过实验测量验证了该运动学模型的准确性，分析了出现误差的原因。成功地抓取了直径为250 μm的虾卵细胞，表明该微夹取器具有良好的操作性。

参考文献：

[1] 宋宇, 郭伟, 孙立宁. 基于微小型移动机器人的微操作系统[J]. 机械工程学报, 2007,43(2):96-103.

[2] 李杨民, 汤晖, 徐青松, 等.面向生物医学应用的微操作机器人技术发展态势[J].机械工程学报, 2011,47(23):1-13.

[3] Roy D. Development of novel magnetic grippers for use in unstructured robotic workspace[J].Robotics and Computer-Integrated Manufacturing, 2015,35:16-41.

[4] Liu J, Gong Z, Tang K, et al. Locating end-effector tips in robotic micromanipulation[J]. IEEE Transactions on Robotics, 2014,30(1):125-130.

[5] Herrero S, Mannheim T, Prause I, et al. Enhancing the useful workspace of a reconfigurable parallel manipulator by grasp point optimization[J]. Robotics and Computer-Integrated Manufacturing, 2015,31:51-60.

[6] 雷志刚, 黄心汉.机器人压电陶瓷微操作手的设计[J]. 兵工自动化, 2004,23(2):21-22,35.

[7] Zubir M N M, Shirinzadeh B, Tian Y. A new design of piezoelectric driven compliant-based microgripper for micromanipulation[J]. Mechanism and Machine Theory, 2009,44(12):2248-2264.

[8] Tanikawa T, Arai T. Development of a micro-manipulation system having a two-fingered micro-hand[J]. IEEE Transactions on Robotics and Automation, 1999,15(1):152-162.

[9] Geng R R, Mills J K, Yao Z Y. Design and analysis of a novel 3-DOF spatial parallel microgripper driven by LUMs[J]. Robotics and Computer-Integrated Manufacturing,2016,42:147-155.

[10] 付前卫,姚志远.用于驱动汽车天窗的直线超声电机设计[J].机械与电子,2016,34(7):30-33,45.

[11] 曹会平,叶明, 姚志远,等. 直线超声电机精密运动平台系统模型辨识[J].机械与电子,2014(4):39-42.