小波包能量熵与EMD结合分析法在风机滚动轴承故障诊断中的应用

，，，

(1.沈阳工业大学机械工程学院，辽宁 沈阳 110870；2.辽宁装备制造职业技术学院自动控制工程学院，辽宁 沈阳 110161；3.中认(沈阳)北方实验室有限公司，辽宁 沈阳 110164)

0 引言

近年来，我国的风力资源开发正在进入一个高速增长期，风力发电的规模也在逐步扩大。由于风力发电机组长期处于载荷多变、风速不稳的工况下，机组的机械部件极易发生故障，其中轴承故障占总故障率的40%以上[1]。轴承出现早期故障时，会使系统出现振动和噪声，若未能及时处理，则可能导致其他传动部件崩溃甚至报废，严重影响风力发电机组的运行[2]。由于轴承拆卸不便，传统的人工维修方式效率低、成本高，这就需要探索轴承故障诊断的新方法、新策略。

轴承作为一种典型的旋转部件，其故障常从振动信号中表征出来，对振动信号的分析与诊断是目前常用的手段[3]。常用的信号分析方法有时域分析、频域分析和时频域分析。其中，时频域分析具有降低强噪声干扰、适应复杂工况的优点，在故障特征提取方面得到了越来越多学者的关注。加拿大卡尔加里大学Sharma 等[4]对多种状态指标的齿轮故障诊断进行了综述。清华大学张智等[5]提出了小波能量熵在铣削振动状态分析中的应用，研究了信号的能量分布规律。西安交通大学雷亚国[6]提出了基于集成经验模态分解的希尔伯特黄变换诊断方法。西安航空学院杨武成[7]提出了一种基于阶次跟踪和Hilbert包络解调的滚动轴承故障诊断方法。南京农业大学钱林等[8]将小波包与质心粒子群理论用于齿轮箱的故障诊断中。这些文献虽然从不同方面描述了振动信号从稳定向不稳定状态演变的阶段性特点，但大多数研究仍停留在实验验证阶段，且单一的分析方法往往不能全面反映振动信号的特征，难以实现对风力发电机组故障的快速、准确、有效的诊断。因此，有必要将传统分析方法结合起来，从多个角度处理故障信号。

针对以上问题，提出了一种基于小波包能量熵与EMD(经验模态分解)联合分析法处理风机轴承故障信号的诊断方法。该方法从能量分布和包络谱分析的角度处理振动信号，可以有效地提取故障特征频率，准确地诊断出故障所在的位置。

1 小波包分析

小波包分析方法可以使信号能量集中，有利于寻找信号的有序性和规律性，是一种更加精细的分析方法，是对小波分析的延伸。它对信号频带进行多层次的划分，对没有细分的高频部分进行更加细致的分解，并能够根据被分析信号的特征自适应地选择频带，使之与信号频谱相匹配，从而提高信号的时域分辨率[9]。

1.1 小波包阈值消噪

使用小波包分析方法处理含有噪声的故障振动信号时，常需要设置阈值来分离特征信号和噪声信号，阈值的选取关系到信号消噪的质量。利用固定形式的阈值可以获得较好的消噪效果，其算法为：

(1)

T为给定阈值；σ为噪声信号的偏差；N为含噪信号在所有尺度上的小波包分解得到的小波系数的个数总和。

小波包对振动信号的消噪处理步骤为：

a.对原始信号进行小波包分解。选择最佳小波包基并确定小波包分解的层数。

b.小波包分解系数的阈值量化。使用固定阈值准则进行高频信号处理，保留低频系统。

c.信号的小波包重构。根据小波包分解保留的低频系数和经过量化处理的高频系数进行小波包重构。

1.2 小波包能量熵

在信息论中，熵常用来度量信息的混乱程度。当信息越确定，越单一，信息熵越小；信息越不确定，越混乱，信息熵越大[10]。

信息熵的计算公式为：

(2)

H(x)为信息熵；P(xi)为若干个xi产生的概率。

在振动信号分析中，熵可以反映幅值波动的程度，而幅值又是能量的体现，故能量熵是一种有效的故障诊断方法。

对于某一信号源，设其信号长度为N，将该信号进行j层小波包分解后，得到m(m=2j)个小波包重构系数序列，计算每个子序列的能量值Ejk，即

(3)

xi(t)为第i个子信号的重构系数；ti和ti-1分别为信号获取的起止时间。

通过计算m个子信号，可以得到一组能量向量[Ej1,Ej2,…,Ejm]，对各能量值进行归一化处理，得到能量比为：

(4)

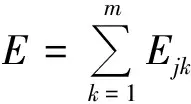
能量熵可由式(5)得到：

(5)

在滚动轴承正常工作时，能量主要集中分布在转频及其倍频处，而当轴承发生故障时，能量会集中在故障频率附近[11]，使得振动信号的能量分布发生变化，依据这一特点，能够有效进行故障特征的提取。

2 EMD模态分解

2.1 EMD方法基本原理

经验模态分解(empirical mode decomposition)简称EMD，是以傅里叶变换为基础的稳态频谱分析方法[12]。它是依据数据自身的时间尺度特征将非线性、非平稳信号分解为有限个本征模函数(intrinsic mode function，简称IMF)，然后在对各本征模函数进行希尔伯特(Hilbert)变换，得到包络谱。

其中，1个本征模函数必须要满足以下2个条件[13]：

a.在整个时间范围内，局部极值点数和过零点数相等或最多相差1个。

b.对于任意时刻，局部极大值包络线和局部极小值包络线均值为0，即信号的波形局部对称。

EMD方法的分解步骤如下所述。

a.找出信号x(t)的所有极值点。

b.用插值法求出所有极大值点形成的上包络线和所有极小值点形成的下包络线，分别记为emax(t)和emin(t)。

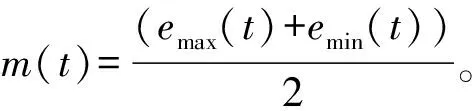
d.抽离信号差d(t)=x(t)-m(t)。

e.判断d(t)是否满足IMF的2个条件，若满足，则d(t)为IMF；若不满足，则记d(t)=x(t)，重复步骤a～步骤c，直到得到1个IMF。

f.重复a～步骤e，得到n个IMF，则原信号可表示为：

(6)

Ci(t)为各IMF分量；Res(t)为信号余项。

g.将得到的IMF分量分别与原信号作相关分析，得到相关系数最大的分量。

2.2 Hilbert包络谱

选取分解后相关系统最大的IMF分量进行Hilbert变换[14]，则有：

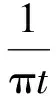
(7)

可见，信号通过Hilbert变换后可对其频率成分作90°的移相。

于是，c(t)的解析信号可写为：

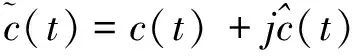
(8)

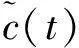
(9)

再对包络进行FFT变换[8]，可得：

(10)

3 实例分析

以某风场G52-58风力发电机组的驱动端轴承为研究对象，进行故障诊断分析。该轴承型号为SKF6205，基本参数如表1所示。

表1 SKF6205滚动轴承参数

当轴承出现局部故障时，损伤点与接触点会产生一个冲击信号，其频率可由轴承的参数求得，计算公式如式(11)～式(14)所示[15]。

外圈故障特征频率为：

(11)

内圈故障特征频率为：

(12)

滚动体故障特征频率为：

(13)

保持架故障特征频率为：

(14)

将表1中的轴承参数代入式(11)～式(14)，得到各部件的故障特征频率如表2所示。

表2 滚动轴承各部件故障特征频率 Hz

当滚动轴承发生故障时，风机由于振动过大报警并停机，测试信号的采样频率为12 kHz，采样点数为4 096，振动信号的时域波形如图1所示。

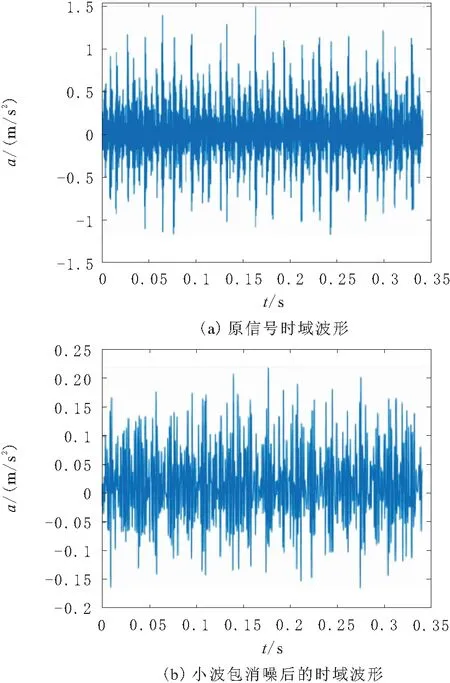
图1 滚动轴承故障振动信号的时域波形

由图1a可知，轴承振动的幅值很大且伴有较大噪声。为了进一步分离特征信号，选取db4小波基对被测信号进行3层分解，对原时域信号信号进行消噪处理，如图1b所示。

再利用能量熵标准分别提取第3层从低频到高频的各频率成分的信号特征，从而得到各子频带的小波包分解节点分别为(3,0),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(3,7)。通过系数重构，得到各频带信号的能量向量和总能量，经过归一化处理后的各频段能量分布情况如图2所示。

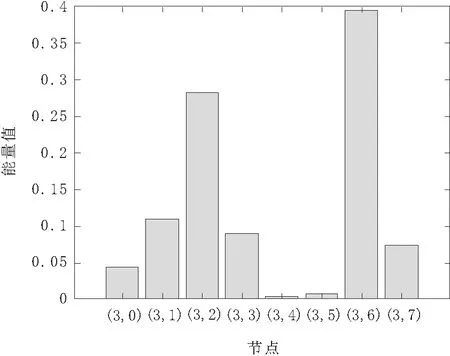
图2 故障频段能量

由图2可知，故障轴承的能量集中分布在节点(3,6)处，其频率为高频段，能量熵较小(计算得1.55，正常工况通常在2.0附近)。为进一步获取信号的故障特征频率，有必要进行进一步分析。

对小波包重构后的信号做EMD模态分解，得到9个IMF分量和1个残余量。

将各IMF分量分别与原信号做相关分析后，得到相关系数如表3所示。

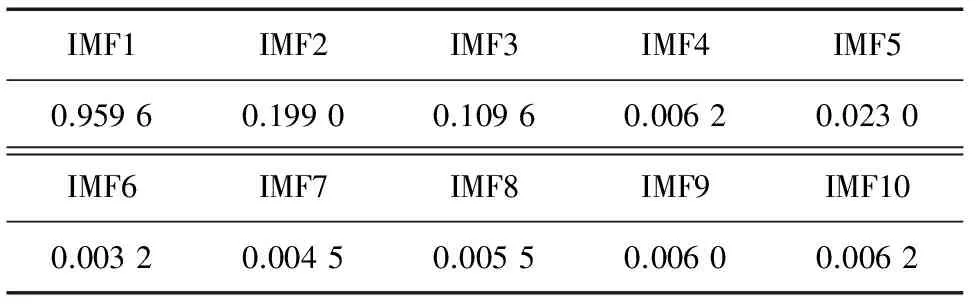
表3 IMF分量的相关系数

由表1可知，IMF1的相关系数最大，该分量能够体现振动信号的主要特征，故选用IMF1做Hilbert包络谱分析，如图3所示。

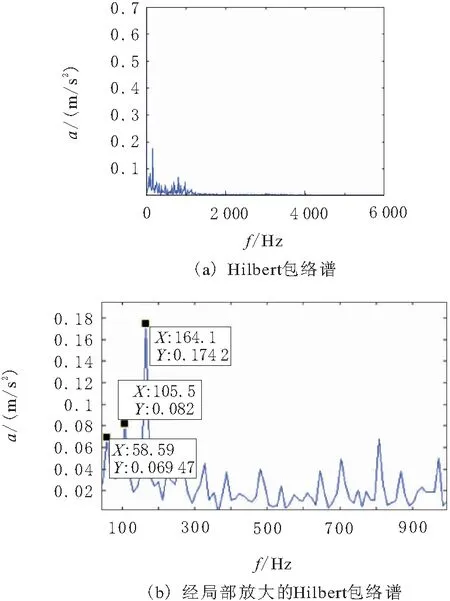
图3 IMF1分量的Hilbert包络谱

图3a体现了包络谱的分布情况，图3b是经过局部处理放大后的包络谱。从包络图可以看出，前3个峰值有明显的谱线，其中最大峰值频率为164.1 Hz，对比表2所示的轴承各部件故障特征频率值，与内圈故障特征频率f2=162.21 Hz相近，说明轴承内圈发生了故障。

4 拆解验证

根据诊断结果，对该台机组的驱动端轴承进行了拆解，如图4所示。

图4 风机驱动端轴承内圈磨损状况

由图4可知，驱动端轴承内圈出现了严重的表面磨损故障，验证了本文提出的诊断方法的正确性和有效性，使故障轴承得到及时的更换并找到了产生故障的原因。

5 结束语

将小波包能量熵理论与EMD分解法结合起来，对风机驱动端的滚动轴承振动信号进行了分析。当滚动轴承发生故障时，其振动信号的时域特性体现了故障点对各频带能量的影响。为了寻找这些隐含着的故障信息，采用小波包变换很好地滤除了原始振动信号中的高频噪声，使振动信号能量与故障状态之间建立起映射关系，通过小波能量熵理论得到了各频段能量分布情况，确定了故障频率所在的频段范围。同时，使EMD分解后得到的IMF分量更准确地反映处故障特征，经过相关性系数计算，选取最能体现故障特征的模态分量进行Hilbert包络谱分析，不仅提高了频率分辨率，还有效避开了其他频率成分的影响，使得故障特征频率的谱峰更加容易识别，拆解实验验证了分析结果的正确有效。这种结合分析法简单实用，诊断结果准确，可为后续风力发电机的故障识别和寿命预测提供有力的理论支撑。

参考文献：

[1] 孔德同，贾思远，王天品，等. 基于振动分析的风力发电机故障诊断方法[J]. 发电与空调, 2017,38(1): 54-58.

[2] 戴耀辉，苗瑞，罗兴铭，等. 基于小波变换和高阶特征提取的直驱风机轴承故障诊断方法[J]. 四川电力技术, 2016,39(6):41-46.

[3] 杨玉昕．风机轴承故障诊断中的振动信号特征提取方法研究[D].秦皇岛:燕山大学，2013．

[4] Sharma V, Parey A. A review of gear fault diagnosis using various condition indicators[J]. Procedia Engineering, 2016,144:253-263.

[5] 张智, 刘成颖，刘辛军，等. 采用小波包能量熵的铣削振动状态分析方法研究[J].机械工程学报, 2017, (9): 1-6.

[6] 雷亚国，贾峰，孔德同，等. 大数据下机械智能故障诊断的机遇与挑战[J]. 机械工程学报, 2018,54(5):94-104.

[7] 杨武成.阶次跟踪和Hilbert包络解调在滚动轴承故障诊断中应用[J].机械科学与技术,2017,36(12):1873-1876.

[8] 钱林，康敏. 基于小波包与质心粒子群的齿轮箱故障诊断及应用[J].振动与冲击,2016,35(11):191-195.

[9] 张智胜,张云鹏,刘青.支持向量机和小波包分析下的轴承故障诊断[J].机械设计与制造,2017(3):204-207.

[10] 高扬，卫峥，尹会生．白话大数据与机器学习[M].北京：机械工业出版社，2017．

[11] 邓飞跃，唐贵基．基于时间-小波能量谱样本熵的滚动轴承智能诊断方法[J].振动与冲击，2017,36(9):28-34.

[12] 何刘，林建辉，丁建明，等．调幅-调频信号的经验模.态分解包络技术和模态混叠[J].机械工程学报，2017，53(2):1-10.

[13] 王利英，孙中伟.EMD在LabVIEW中的实现及其在水轮机主轴振动信号分析中的应用[J].水电能源科学,2017,35(2):185-188.

[14] 朱永利，贾亚飞，王刘旺，等．基于改进变分模态分解和Hilbert变换的变压器局部放电信号特征提取及分类[J].电工技术学报,2017,32(9):221-235.

[15] 孙鲜明，刘欢，赵新光，等．基于瞬时包络尺度谱熵的滚动轴承早期故障奇异点识别及特征提取[J].机械工程学报,2017,53(3):73-80.