非平稳强噪条件下的视频相位放大技术研究

,

(中国科学技术大学精密机械与精密仪器系，安徽 合肥 230026)

0 引言

使用高速相机拍摄视频分析物体的振动，相比传统接触式测量不会带来质量负荷，而且成本更低，分辨率更高。但是有时物体的振动很微弱，对于人眼来说很难察觉，需要放大后才能更好地观察。传统的线性欧拉放大技术[1]在高空间频率时只能放大较小的倍数，并且当放大倍数增大时，噪声也会被放大。

Wadhwa提出了基于复数金字塔的视频运动处理技术[2-3]，依据在图像的一个空间子带中复数金字塔的相位变化正比于局部运动的原理[4]，计算局部相位的变化并对选定的频率范围做带通处理，再将放大处理后的信号重构为视频。这种基于相位的方法可以达到更大的放大倍数和更好的噪声表现。但是这种方法在处理非平稳信号时，带通滤波器需要选择较大的频带范围，在此频带范围内存在的噪声也将被放大，所以需要更好的方法来处理宽频带内的噪声。时频滤波[5]是一个比较理想的选择。同时对每个像素点进行时频处理会大大增加计算量，降低运算速度。

在此，提出了一种基于参数化时频分析[6]及主成分分析(PCA)[7]的滤波方法，来放大非平稳强噪视频信号。相比于传统相位视频放大技术，这种方法可以有效提取非平稳信号并实现原始视频信号的放大。

1 时变视频相位放大技术

1.1 相位放大原理

在空域，根据复数可控金字塔原理，将图像序列I(m,n,t)多分辨率分解为：

A(γ,θ,m,n,t)eiψ(γ,θ,m,n,t)

(1)

γ表示尺度；θ表示方向。在时域，依据t0时刻的相位可以计算出t时刻的相位变化量：

δ(γ,θ,m,n,t)=ψ(γ,θ,m,n,t)-ψ(γ,θ,m,n,t0)

(2)

(3)

但是这种方法在处理非平稳信号时，往往需要选择较大的带宽，此带宽内的噪声信号也将会被放大，此时就无法有效地提取所需要的信号，所以要从时频角度来分析提取信号。在此之前，需要了解信号时频分布类型，才能选择有效的滤波器。

根据Davis的研究，对相位变化信号进行幅值加权，可以得到局部振动信号：

Φi(γ,θ,t)=∑m,nA(γ,θ,m,n,t)2δ(γ,θ,m,n,t)

(4)

那么进一步，可以得到全局振动信号：

(5)

1.2 PCA降维和时频滤波

通过复数金字塔可以将各尺度方向上相位随时间变化的信号δ(m,n,t)提取出来，但是对每个像素点的δ时频变换，计算量巨大，耗时严重。为解决这个问题，采用PCA将δ降维，对降维后的信号做时频处理。将时刻j的δ重排为一列向量δj∈RK×1，其中K=M×N，则δ(m,n,t)可以表示为：

X=[δ1,δ2,δ3,…,δT]

(6)

PCA分解是指对矩阵X∈RK×T，存在特征向量矩阵U∈RK×K和特征值矩阵D∈RK×K满足下列方程：

XX′=UDU′

(7)

将特征向量按对应特征值大小从上到下按行排列成矩阵，取其前r行组成矩阵P∈Rr×K，那么就可以得到降维到r维后的数据：

Y=PX

(8)

(9)

1.3 算法流程

基于参数化时频分析和PCA降维处理原理，提出了针对非平稳强噪声的视频相位放大技术。具体流程如图1所示，算法描述如下：

a.将视频信号I通过复数金字塔分解，提取图像相位信号ψ和幅值信号A。

b.对相位信号ψ在时间维度上做差分求出相位变化信号δ，对其幅值加权求和，得到对应尺度方向上的局部振幅Φ，再对各尺度方向求和得到全局振幅s(t)。

c.对s(t)做参数化时频分析，得到时频脊线函数，选择带宽，构造时频模板ymask。

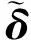
图1 时变视频放大方法流程

2 实验分析

2.1 转子振动信号采集实验

实验数据采集平台如图2所示。振动信号采集系统包括Basler acA2000高速摄像机、光源、转子实验台和台式机电脑。转子实验台电机为三相异步电机，型号为YE2-8012，电机驱动器型号为MICROMASTER440。

设置电机最高转速为3 000 r/min，依据驱动器设置电机将在10 s内匀减速至停止。实验中，相机分辨率设置为400像素×1 024像素，采样率为392 Hz，一次采样3 000帧。

图2 实验设备

2.2 振动信号提取分析

根据Davis的方法，分析得到电机降速过程中转子振动信号的波形如图3所示，对其做STFT，可以看出振动频率随时间近似线性减小，但是在27 Hz处存在能量较高的干扰频率，严重影响视频相位放大的结果。

用多项式参数化时频分析方法处理该信号，假设其时频函数为：

f(t)=z0+z1t+z2t2+z3t3

(10)

求得z0=36.627 5，z1=-5.096 2，z2=-0.002 9，z3=0.008 9，其斜率与实际频率变化率5 Hz近似一致。选取图像金字塔分解得到的某一尺度、方向上图像一像素点的相位变换信号δ进行时频分析，其波形及时频如图4所示。

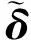
图3 视频麦克风信号波形和时频

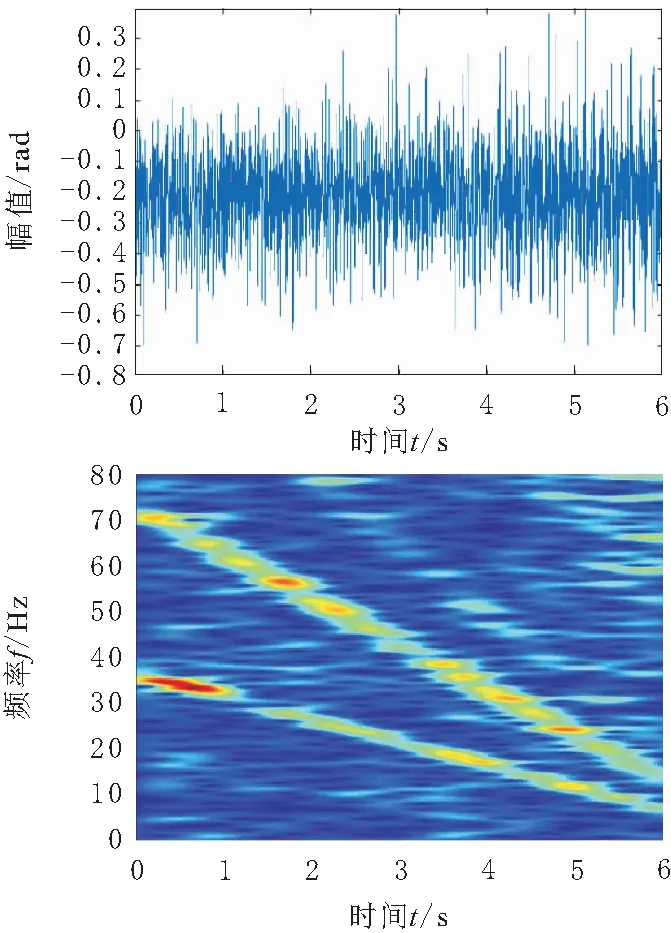
图4 原始相位变化波形与时频

设置放大系数12倍，对滤波后的相变信号重构，得到重构视频。放大前和放大12倍后视频对应帧对比如图6所示，其中，上图表示放大处理前的原始视频图片，下图表示放大处理后的视频图片。图6a表示处理前后视频对应帧图像，由于处理时为加快运行速度，对图像做了缩放，所以下图相对模糊。图6b表示取视频在100～300帧(0.255～0.765 s)的切片组成的图片，可以看出处理后轴发生明显振动，并且振动频率较快。图6c表示视频在1 800～2 000帧(4.592～5.102 s)的切片组成的图片，可以看出电机转速降低后，对应的振动频率也变慢了。

在MATLAB2017中，在没有使用PCA方法时，直接对各像素点时频滤波，在单一尺度、方向上运算时间超过半小时，而使用PCA降维处理，则运算时间降低至130 s左右，说明PCA方法有效降低运算量，大大提高运行速度。

图5 降维滤波后信号波形与时频

图6 处理前后图像对比

3 结束语

提出了一种基于参数化时频分析和PCA降维算法的视频相位放大方法，用于将物体的微小振动放大，便于观察和分析。相比于传统的视频相位放大方法，所提方法更加针对非平稳振动信号，因此，该方法在消除噪声干扰和放大非平稳信号上具有明显优势。实验结果表明，该方法能有效地提取电机降速过程中转子振动频率，并可将视频中转子振幅放大。

参考文献：

[1] Fuchs M, Chen T, Wang O, et al. Real-time temporal shaping of high-speed video streams[J]. Computers and Graphics, 2010, 34(5): 575-584.

[2] Simoncelli E P, Freeman W T.The steerable pyramid: a flexible architecture for multi-scale derivative computation[C]// Proceedings of the IEEE International Conference on image Processing，1995, 3: 444-447.

[3] Wadhwa N,Rubinstein M,Durand F,et al.Phase-based video motion processing[J]. ACM Transactions on Graphics (TOG), 2013, 32(4): 80.

[4] Davis A,Rubinstein M,Wadhwa N, et al. The visual microphone: passive recovery of sound from video[J].ACM Transactions on Graphics (TOG),2014,33(4): 79.

[5] 李燕,魏宗信,刘军.机电系统振动信号分析技术的研究[J].机械与电子,2010(2):30-32.

[6] 杨扬.参数化时频分析理论、方法及其在工程信号分析中的应用[D].上海：上海交通大学,2013.

[7] Yang Y, Dorn C, Mancini T, et al. Blind identification of full-field vibration modes from video measurements with phase-based video motion magnification[J]. Mechanical Systems and Signal Processing, 2017, 85: 567-590.