高速铁路列车运行线铺画模型与算法设计
, , ,
(1.交通运输部管理干部学院,北京 101601;2.北京赛宝工业技术研究院有限公司,北京 100041;3. 中铁物资集团华北有限公司,河北 石家庄 050000;4.石家庄铁道大学 交通运输学院,河北 石家庄 050043)
0 引言
我国的专家学者对于列车开行方案和计算机编图的研究开始于20世纪60年代。众多学者[1-7]先后开展了大量相关研究工作,经过多年对列车运行图的深入研究,积累了丰富的理论方法和实践经验,提出了动态规划法、统筹图方法、分支定界法、原始对偶法、区间推进法、时间循环迭代法以及动态系统法等优化方法。论文基于高中速混跑模式,构建了我国高速铁路列车运行线铺画模型,采用遗传算法进行求解,能够为我国高铁系统列车运行线的自动智能铺画提供理论和决策参考。对高铁系统建设的现代化具有十分重要的理论意义和实用价值。
1 高速铁路列车运行线铺画模型构建
1.1 模型假设
(1)本模型针对单条复线高速铁路线路,线路采取高中速列车共线运行模式。列车的开行方案已知,列车开行频率已知,列车停站方案已知。(2)铺画列车运行图所需的各种参数已知,需铺画线路的沿线车站名称、区间里程、各车站到发线数量等线路数据已知。(3)把列车的等级分为两类,一类时速300 km/h的A类列车后文称高等级列车,一类时速200 km/h的B类列车后文称低等级列车,模型不考虑同等级列车之间的越行。(4)本文所列模型仅适用于计划阶段的列车运行图编制,而不适用于列车运行图的调整规划。(5)假设需铺画线路的各车站到发线满足本文模型中到发线约束条件。
1.2 参数定义
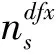
1.3 约束条件
(1)列车区间运行时间约束
(1)
(2)
(s,s+1)为上行方向,(s+1,s)为下行方向,下同。
(2)车站停站时间约束
(3)
(4)
(3)追踪列车间隔时间约束
(5)
(6)
(7)
(8)
(4)车站间隔时间约束
(9)
(10)
(11)
(12)
(5)车站发车、到达时间域约束

(13)

(14)

(15)

(16)
(6)车站到发线约束。在任意时刻t,在车站s同时停留的列车数不能大于车站到发线数量,当车站到发线分上下行方向使用时,应分别考虑上行和下行的到发线约束,定义函数
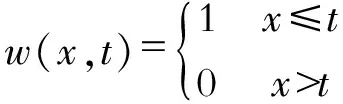
(17)
则到发线约束为
(18)
车站到发线分上下行方向使用时,上下行列车使用到发线约束分别为
(19)
(20)
(7)列车越行约束。两列同向列车经过相同区间应满足区间越行关系约束,分为如下4种情况:
①同等级列车之间不能相互越行(不考虑同等级之间的越行);②高等级列车可以越行低等级列车;③低等级列车禁止越行高等级列车;④一列低等级列车最多连续被两列高等级列车越行;⑤一列高等级列车最多连续越行一列低等级列车。
(8)天窗约束。a为天窗开始前最后一列车与天窗之间的最小间隔时间;β为天窗结束后发车的第一个列车与天窗之间的最小间隔时间。
(21)
(22)
(23)
(24)
1.4 目标函数
以列车总旅行时间最小为目标
(25)
式中,w1(i)、w2(i)分别代表上、下行列车的等级系数,列车等级越高系数越大,可以确保高优先级列车优先权。本文构建了以列车总旅行时间最小为目标函数,8个约束条件的数学模型。
2 列车运行线铺画的优化算法设计
2.1 遗传算子设计
本算法选择染色体编码方式为整数编码,每个染色体定义为n层,每一层代表着一个区间的列车发车顺序,比如第1层编码代表列车在始发站的发车顺序,第k层编码代表第k个区间的列车发车顺序,编码的初始化令所有的区间列车发车顺序相同。

本文采用部分匹配交叉算子来保证基因的唯一性和完整性。本文模型编码初始化每一层编码的序列是相同的,如果仅仅随机一行进行交叉操作,那么交叉后的个体编码中只有一行与其它行不同,这样的个体编码满足越行约束的概率是极小的,所以本文采用全部行都进行交叉操作的策略。
2.2 遗传解码策略
在遗传算法中,编码操作和解码操作互为逆操作,在用遗传算法求解列车运行线铺画模型中,编码表示在每个区间列车的发车顺序,解码就是根据确定的列车发车顺序求解列车在每个车站的到发时刻。
解码步骤如下:
始发站定义为第0站,按照线路下行方向依次为第1站、第2站,…,第n站,时间单位以分钟计,例如6:05即为365,13:15计为795,一天时间为0~1 440。

(1)计算第0站的列车发车时刻。取个体编码的第一行编码[1,3,2,5,4],按照编码顺序,设第1列车的始发时间为360(满足了列车发车时间域约束),第2列车的始发时间为前行列车的始发时间加上列车最小发车间隔(满足列车最小发车时间间隔约束),依次类推,求出第0站所有列车的始发时刻。
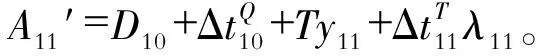





3 算例
本文采用的京沪高速铁路数据主要有车站名称、车站的到发线数量、高等级列车在区间的运行时间、低等级列车在区间的运行时间。实例的开行方案在现有列车时刻表的基础上修改得到。(1)列车运行图参数设置如下:停车附加时间 ,高等级列车为3 min,低等级列车为2 min;启动附加时间2 min,停站时间3 min;追踪间隔时间4 min;同方向列车最小到达间隔时间2 min;同方向列车最小发车时间间隔2 min;天窗时间:0点~4点。(2)遗传算法的参数设置。本文的遗传算法设计中参数设置如下所示:最大迭代次数maxgen = 1 000;种群规模popsize = 20;交叉概率:pc = 0.6;变异概率pm = 0.3。列车运行线铺画仿真结果如图1。

图1 列车运行线铺画仿真结果
在本实例铺画的列车运行图中可以看出D1次列车在沧州西连续被G7、G43越行,在德州东被G45越行,在济南西被G47越行,在滕州东连续被G49、G9越行,在枣庄西被G21越行,在徐州东连续被G51、G53越行,D1最多连续被两列高等级列车越行,而一列高等级列车最多连续越行一列低等级列车,完全符合列车越行约束。
4 结论
采用遗传算法求解高速铁路列车运行线铺画模型,设计了n层编码方式,以列车总旅行时间的倒数为适应度函数,采用轮盘赌选择算子,改进的部分匹配交叉方法,改进的两点变异方式,以适应本模型的二维矩阵编码,保证了染色体编码的唯一性,设计列车越行约束检查算法,在每个遗传操作结束后均进行越行约束检查,引导遗传进化往好的方向发展,并详细说明了其它约束条件的处理方法;以MyEclipse10为平台,开发设计了计算机铺画列车运行线仿真系统,并以京沪高速铁路为背景,铺画了47对高等级列车、3对低等级列车,总共50对列车的运行线,输出了列车时刻表,验证了模型和算法的有效性。
参 考 文 献
[1]张英贵. 铁路客运站股道运用优化方法与应用研究[D].长沙:中南大学,2012.
[2]朱向,雷定猷. 带平衡约束三维装箱问题的双层混合遗传算法[J].交通运输系统工程与信息,2015,2:203-209.
[3]马建军,胡思继. 基于网状线路的京沪高速铁路列车运行图编制理论的研究[J].中国铁道科学, 2002,23(5):135-137.
[4]彭其渊,杨明伦. 计算机编制复线实用货物列车运行图的整数规划模型及求解方法[J].中国铁道科学, 1994,15(4):60-66.
[5]倪少权,杨明伦. 计算机编制全路直通旅客列车运行图的研究[J].铁道运输与经济, 2002, 24(6),41-43.
[6]Tormos P. A genetic algorithm for railway scheduling problems [J].Studies in Computational Intelligence, 2008,128: 255-276.
[7]李明. 遗传算法的改进及其在优化问题中的应用研究[D].长春: 吉林大学, 2004.

