断裂过程区内聚力分布对简支梁刚度和自振特性的影响研究

， ， ，

(石家庄铁道大学 土木工程学院，河北 石家庄 050043)

0 引言

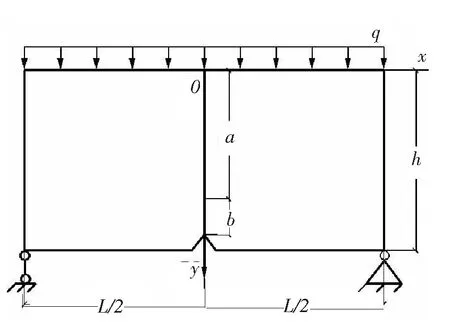
图1 均布荷载作用下带裂缝简支梁

由Dugdale[1]提出的模型可应用于理想弹塑性断裂[2-4]，但并不适用于混凝土类拉应变软化材料。根据混凝土的变形特点，Hillerborg[5]于1976年提出了“虚裂纹模型”(简称FCM)；Bazant[6]于1983年提出了“钝裂纹带模型”(简称BCBM)。FCM、BCBM等模型虽然较好地反应了混凝土等软化材料在断裂过程区的应力和变形特点，但不能从数学上对过程区应力分布进行解析求解。20世纪八十年代，段树金等提出了有限应力集中的概念，采用加权积分法和奇异曲面叠加法得出了过程区应力场解析解，该模型在国际上被称为“Duan and Nakagawa’s Model”[7-10]。郭全民等[11]用函数叠加法得出了含断裂过程区简支梁在均布荷载作用下的应力函数全场解析解并通过仿真验证了解的可靠性，但所取函数数量不足导致裂纹面上呈现了较大应力。本文基于“Duan and Nakagawa”模型和文献[11]；叠加多种不同荷载作用、不同裂纹长度下无限大板的弹性解答，得到含断裂过程区的简支梁的更高精度的解析函数；研究不同断裂过程区内聚力分布对拉应变软化曲线和梁自振频率的影响。

1 基本问题与基本方程

1.1 研究对象

研究对象为含切口和断裂过程区的简支梁，如图1所示，其中，a+b为韧带长度，b为断裂过程区长度。

1.2 基本方程

引用复变函数，弹性力学平面问题应力函数的一般形式可表示为

(1)

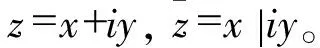
(2)

(3)

式中，G为剪切弹性模量；对于平面应变问题k=3-4v，对于平面应力问题k=(3-v)/(1+v),v为泊松比。

(1)弯矩作用下对称边裂纹的无限大板。如图2所示，为一对称边裂纹的无限大板受弯曲作用，采用加权积分法，取一次型权函数，通过加权积分法消除裂纹尖端应力奇异性，弹性解答如下[5]

(4)

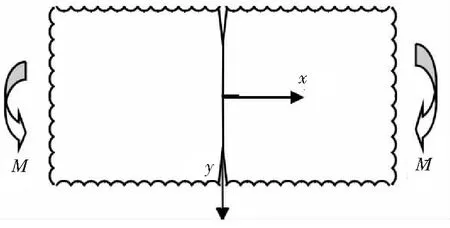
图2 弯矩作用下无限大板

(2)均布荷载作用下的简支梁。考虑一均布荷载作用下的简支梁，其中h为梁高，l为梁长，q为梁上均布荷载。直接给出相应的应力分量

(5)

(3)切应力作用下的半无限大板。如图3所示，为一半无限大板，其自由表面作用着对称于y轴的剪应力，用于消除前述第(1)项中沿x轴产生的剪应力。其相应的应力函数为

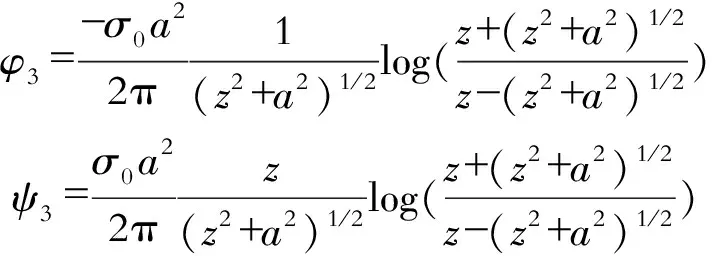
(6)

(4)拉应力作用下的无限大板。考虑一带对称边裂纹的无限大板，在无穷远处受拉应力作用，如图4所示。其应力函数为

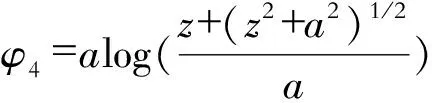
(7)

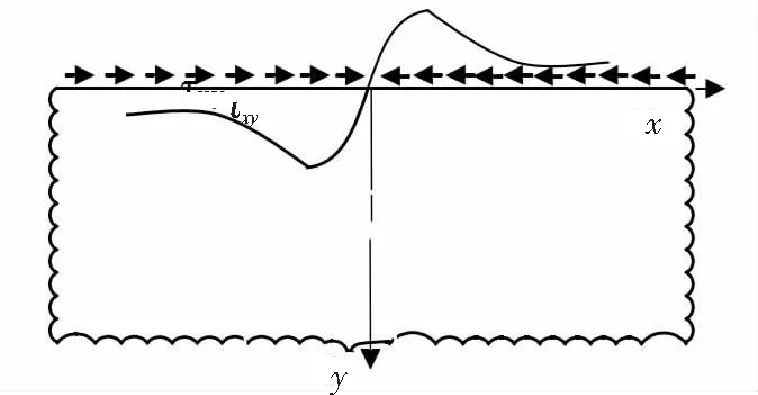
图3 受切应力作用的半无限大板

图4 受拉力作用的开裂板

2 不同内聚力分布下问题的求解

研究的裂缝模型满足以下条件：

(1)梁的有效高度为韧带长度和断裂过程区长度之和a+b。

(2)裂缝尖端y=a处正应力达到抗拉强度ft，即∑σ=ft时，裂缝向前扩展，并始终沿y轴方向。

(3)梁截面有效高度范围内应力合力为零，即∑T1j=0。

(4)梁端弯矩和正应力合力为零，即∑T2j=0，∑Mj=0；梁底一半的正应力和切应力的合力为零，即∑T3j=0，∑Qj=0。

设带裂缝无限大板受弯矩作用时荷载大小为X1，均布荷载作用下简支梁受力大小为X2，半无限大板受切应力作用大小为X3，半无限大板受水平集中力作用大小为X4，韧带宽度a不变，改变受弯矩作用带裂缝无限大板的断裂过程区长度b，对应荷载大小为X5，X6，X7，改变均布荷载作用下简支梁梁底位置，对应荷载大小为X8，X9。通过叠加几种无限大板和半无限大板的弹性解答，计算各种模型权重。

2.1 水压力型分布

定义断裂过程区[a,a+b]处应力分布呈水压力分布，现指定

基于上述条件，可以得到以下平衡方程

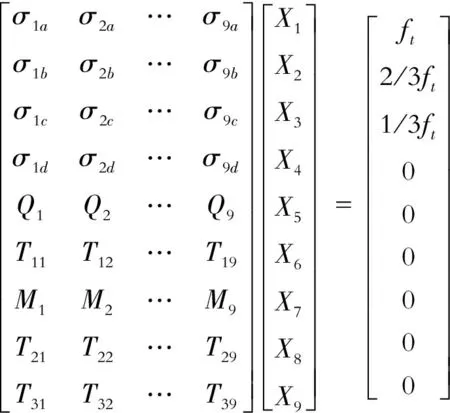
(8)

从中可以求得[Xi]=[-3.598 3 -0.007 9 -0.329 9 3.431 2 0.000 9 -5.664 3 10.642 0

-0.107 0 0.175 9]。

2.2 恒定型分布

定义断裂过程区[a,a+b]的应力为常数，现域内以等距离取3个点，其应力值等于ft，由此可以得到以下平衡方程

(9)

从中可以求得[Xi]=[-8.448 0 0.048 9 -1.937 6 12.127 0 0.002 1 -2.636 0 12.175 7 -0.214 0 0.197 2]。

2.3 一次权函数型

断裂过程区不设约束条件，基于上述边界条件，其相应的平衡方程可以表示为

(10)

由矩阵可以得到[Xi]=[2.402 4 0.010 7 -1.688 7 8.157 1 0.000 9 0.750 2 -1.895 5]。上述方程中的Xi为各基本应力函数在解中的权重，通过叠加即可以得到图1所示问题的应力函数和位移函数。

3 算例

一混凝土简支梁，高度H=8 cm，宽度B=7.5 cm，长度L=30 cm，裂缝长度1 cm，混凝土抗拉强度ft=5.6 MPa，泊松比v=0.2，弹性模量E=28 GPa。

由应力函数得出沿y轴的正应力分布及断裂过程区的拉应变软化曲线，分别如图5和图6所示。从图5可以看出，裂纹尖端应力奇异性被消除；应力最大值出现在断裂过程区尖端；满足正应力合力为零的条件；裂纹面上正应力不等于零，但波动幅度不大。从图6看出，一次权函数型与内聚力水压力型的拉应变软化曲线相似；内聚力恒定型的最大张开位移远小于一次权函数型和内聚力水压力型。梁的自振频率和断裂能如表1所示，带裂缝简支梁自振频率低于无裂缝简支梁，恒定型自振频率高于水压力型与一次权函数型。

图5 沿断裂韧带正应力分布

图6 拉应变软化曲线

考察了梁顶和梁底面切应力的分布，其值不完全为零，切应力最大值与抗拉强度比值分别为4.8%和7.3%。

表1 简支梁的自振频率和断裂能

4 结论

研究了含切口和断裂过程区简支梁的解析，给出了算例，结论如下：

(1)采用函数叠加和选点法得到了带裂缝和断裂过程区简支梁在均布荷载下的全场解析解，基本满足应力边界条件；随着选点数量的增加，可以进一步提高计算精度。

(2)内聚力呈水压力型分布与一次权函数下拉应变软化曲线有相似的变化趋势；内聚力恒定型断裂能最大，水压力型与权函数型断裂能较小且数值相近。

(3)无裂缝简支梁自振频率最高，内聚力恒定型次之，水压力型和一次权函数型时最低。

参 考 文 献

[1]Dugdale D S. Yielding of steel sheets containing slits[J]. Mech. Phys. Solids, 1960(8):100-104.

[2]Li Wu, Xie Lingyun. A Dugdale-Barenblatt model for a strip with a semi-infinite crack embedded in decagonal quasicrystals[J]. Chin. Phys. B, 2013, 22(3):1-6.

[3]杨林. 带单边裂纹的有限狭长体的Dugdale-Barenblatt模型[J]. 山东大学学报：理学版, 2013, 48(8): 63-67.

[4]王慧晶, 林哲. 塑性区模型损伤修正及其对声发射活动的影响[J]. 船舶力学, 2011, 15(4):389-393.

[5]Hillerborg A. Analysis of fracture by means of the fictitious crack model particularly for fiber-reinforced concrete[J]. Int. J. Cement Compos, 1980,2(4): 177-184.

[6]Bazan Z P,OH B H. Crack band theory for fracture of concrete[J]. Mater. Struct., 1983(16):155-177.

[7]Duan S J, Nakagawa K. Stress functions with finite stress concentration at the crack tips for central cracked panel[J]. Engng Fracture Mech, 1988, 29(5): 517-526.

[8]Duan Shujin, Nakagawa K. A mathematical approach of fracture macromechanics for strain-softening material[J]. Engineering Fracture Mechanics, 1989,34(5/6): 1175-1182.

[9]段树金. 断裂过渡区长度张开位移和J积分的计算[J]. 石家庄铁道学院学报, 2000,13(3):6-9.

[10]段树金. 断裂过程区解析理论[M]. 北京: 中国水利水电出版社, 2013.

[11]郭全民, 段树金. 混凝土简支梁在均布荷载作用下的断裂过程区及自振特性[J]. 石家庄铁道大学学报:自然科学版, 2017, 30(2): 6-10.