重型汽车轮胎径向刚度实验研究

, ，2,

(1.石家庄铁道大学 机械工程学院，河北 石家庄 050043；2. 河北省交通安全与控制重点实验室，河北 石家庄 050043)

0 引言

轮胎是底盘的核心，是车辆系统的唯一接地部件，也是车辆在行驶过程中的主要减振元件，起到支撑整个车辆，并与悬挂元件共同抑制路面不平引起的振动和冲击等作用[1-2]。轮胎的动力学特性对汽车的操纵稳定性、制动安全性、乘坐舒适性及NVH性能等都有重要的影响。刚度是描述轮胎动力学特性的主要参数之一，对轮胎径向刚度的非线性特性进行研究具有非常重要的意义。目前，各国学者对于轮胎刚度、阻尼及其影响因素的研究取得了一定的进展。庄继德研究了子午轮胎和斜交轮胎的刚度特性，分析了滚动速度、激振频率和振幅等对轮胎动态刚度的影响[3]。陈栋华等通过分析轮胎变形量、充气压力和振动频率等对轮胎刚度和阻尼的影响，建立了轮胎刚度和阻尼的非线性解析模型[4]。胡林等通过建立三维非线性有限元模型，计算出了30.00R51 子午线轮胎的径向刚度、侧偏刚度和切向刚度[5]。聂信天等对农用轮胎径向刚度和阻尼系数进行试验研究，得出了农用拖拉机导向轮与驱动轮轮胎径向刚度和阻尼系数的回归公式[6]。Reza N. Jazar分析了轮胎加卸载曲线不重合产生的机理，将轮胎力分为刚度力和阻尼力两部分，并分别建立了非线性模型和线性模型[7]。但是，对于重型汽车轮胎径向刚度非线性特性的研究尚不多见。本文主要对重型汽车轮胎在静态和非滚动动态激励下的径向刚度进行实验研究，并建立了非线性解析模型。

1 轮胎径向刚度实验及结果分析

购置重型车用10.00R20子午线轮胎，采用静态加载-卸载法测试轮胎的静态刚度，采用非滚动动态激励法测试轮胎的动态刚度，动态激励采用正弦激励。将轮胎装配在实验台架上，利用弘达HT-9711测试系统完成测试，如图1所示。通过改变静载荷、充气压力和激振频率等，共进行了64种工况的测试。

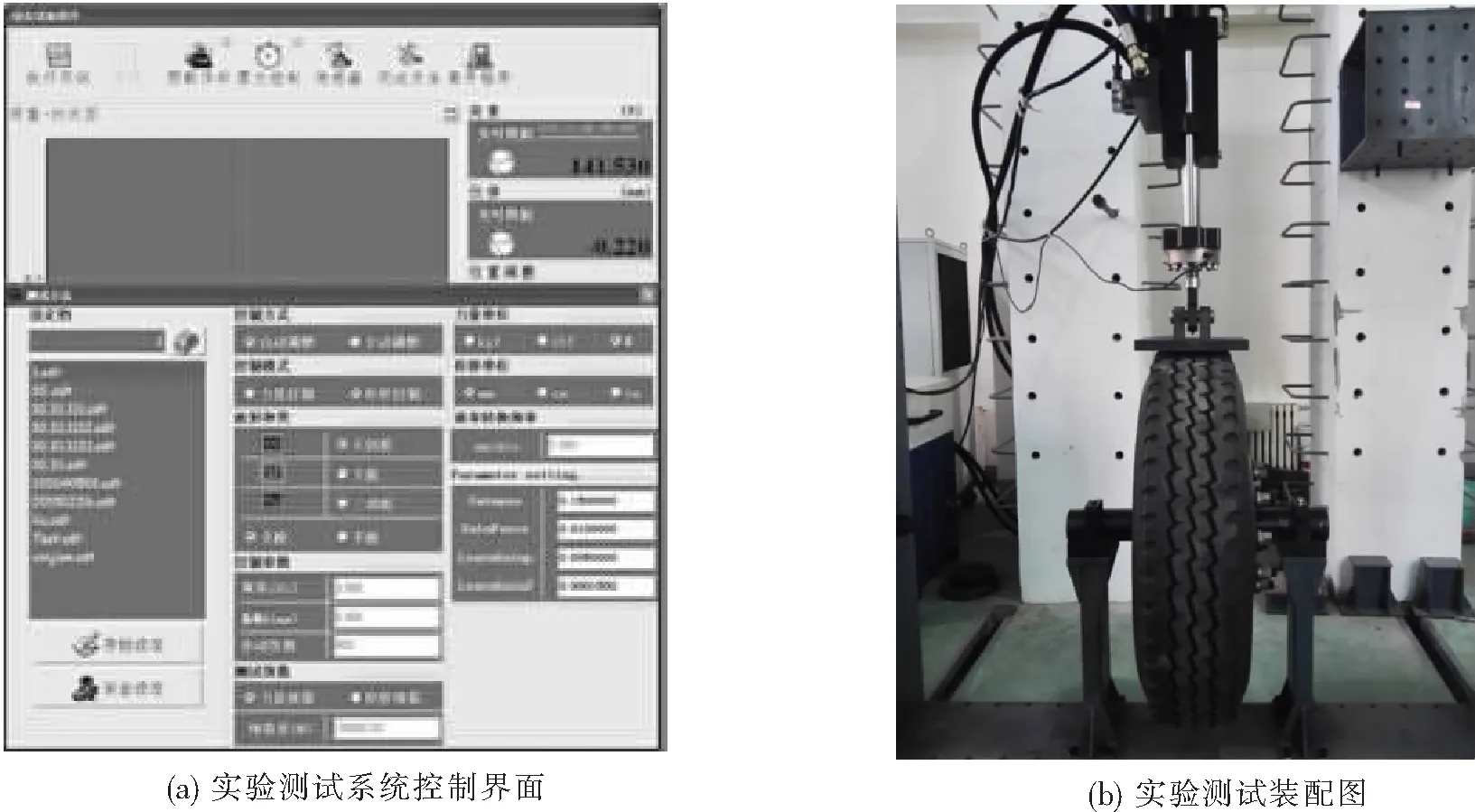
图1 轮胎径向刚度实验测试系统界面及其实验装配图

1.1 轮胎静态径向刚度实验及结果分析

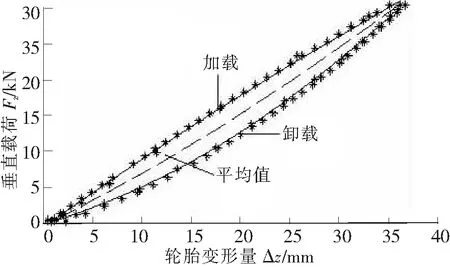
图2 胎压为830 kPa实验数据处理图形

进行静态刚度测试实验时，分别对在充气压力为480 kPa、550 kPa、620 kPa 、690 kPa、760 kPa和830 kPa等状态下的轮胎进行加载-卸载测试。根据轮胎额定载荷值，进行加载载荷设置：起点为0，步长为2 kN，最大终止载荷为30 kN。通过分析实验结果发现：轮胎力在一个加载-卸载循环内的加卸载曲线并不完全重合。这是因为轮胎橡胶是一种粘弹性材料，在经历重复周期变形和恢复时，会因为热量消散而损失能量，从而产生迟滞特性[7-8]。图2为轮胎充气压力830 kPa时的加卸载测试曲线。为了准确地表达轮胎的静态径向刚度特性，采用加卸载变形的均值来表征轮胎的静态径向刚度曲线，称之为轮胎静态刚度力曲线[4]。轮胎静态径向刚度力曲线上的横坐标值为轮胎的径向变形量Δz，纵坐标值为轮胎所受垂直载荷FZ，轮胎的静态径向刚度为垂直荷载的增量∂FZ与径向变形的增量∂(Δz)之比，即轮胎静态刚度力曲线的斜率[7]。

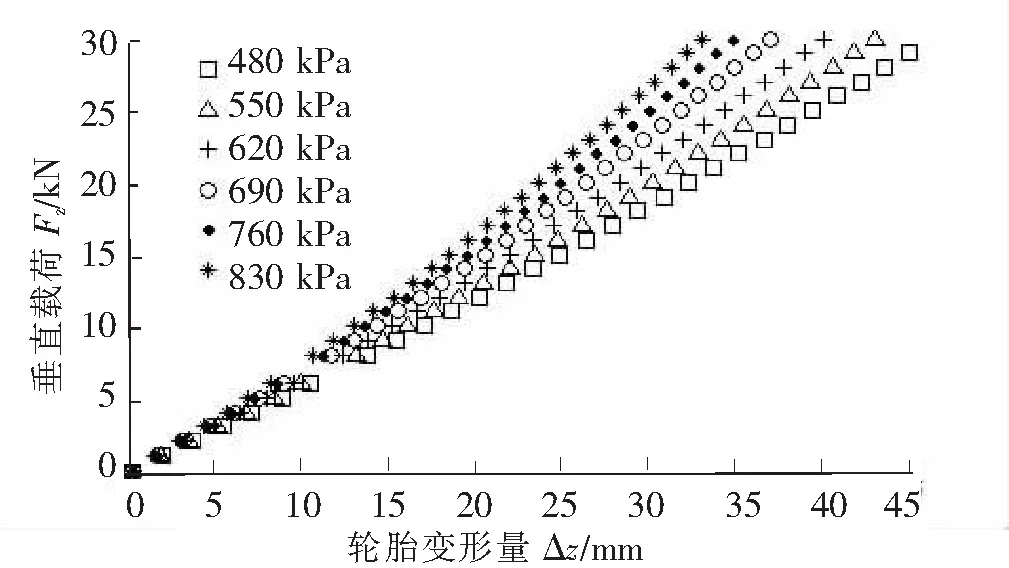
图3 不同胎压下轮胎变形量与垂向载荷之间的关系图

对不同压力状态下的实验数据，采用加卸载变形的均值来表征轮胎的静态径向刚度曲线的方法进行处理，得到各压力状态下的静态径向刚度曲线，如图3所示。由图3可以发现：当轮胎充气压力一定时，随轮胎径向变形量的增大，轮胎静态径向刚度增大，且呈现出非线性特性；不同充气压力状态下，随着轮胎充气压力的升高，轮胎静态径向刚度增大。

1.2 轮胎动态径向刚度实验及结果分析

进行动态刚度测试实验时，对不同充气压力(同静态测试实验)状态下的轮胎采用不同频率的正弦信号进行激励，预加载荷设置为10 kN，正弦激励频率范围为1.0～10.0 Hz，激励振幅为5 mm。其中，轮胎充气压力为830 kPa时，不同激振频率下的轮胎动态径向刚度力线如图4所示。

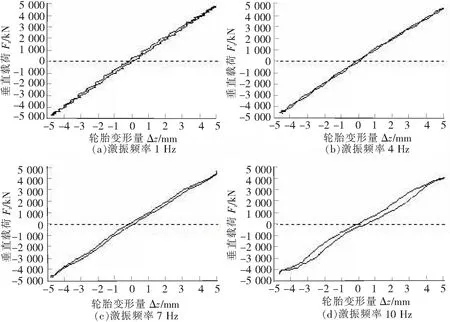
图4 不同激振频率下的轮胎动态径向刚度力线

通过分析发现：在特定的充气压力和激振频率状态下，轮胎力在一个振动循环内的加卸载曲线并不重合；当轮胎充气压力一定时，任一振动循环内轮胎的动态径向刚度随轮胎径向变形量的增大而增大；不同的充气压力状态下，动态径向刚度随充气压力的升高而增大；不同激励频率下，轮胎的迟滞特性存在差异；激振频率较高时，迟滞特性较为明显，滞回环的面积较大，在加载-卸载循环内能量损耗较大。

2 轮胎径向刚度模型的建立

径向刚度是轮胎的主要特性，对车辆振动分析的结果起到关键作用[7，9]。如何建立更为准确的反映轮胎刚度非线性特性的模型，一直以来备受学者们关注。本文基于实验测试数据，分别建立了静态径向刚度非线性模型和动态径向刚度非线性模型。

2.1 静态径向刚度模型的建立

通过分析实验测试结果可知，轮胎的变形量和充气压力是影响轮胎静态径向刚度的主要因素。因此，在建立静态径向刚度非线性模型时，主要考虑这两个因素。为了准确地表达轮胎的非线性特性，采用最小二乘法，对不同充气压力状态下的实验测试数据进行曲线拟合，得出垂直载荷Fz与轮胎变形量Δz之间的数值关系。经过对比分析发现，选取二次多项式较为合理，即

Fz=k1·Δz+k2·Δz2

(1)

式中，Fz为垂直载荷；Δz为轮胎变形量；k1、k2为静态径向刚度系数。得到轮胎在不同压力状态下的k1和k2值，如表1所示。

表1 轮胎静态径向刚度系数

通过对表1中实验数据的分析，可以得到静态径向刚度系数k1、k2随轮胎充气压力p的变化趋势，如图5所示。

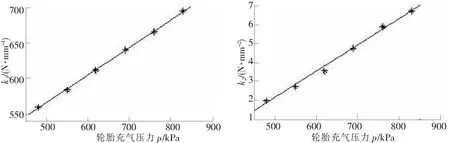
图5 k1、k2值随轮胎充气压力的变化关系

从图5可以看出，静态径向刚度系数k1、k2均与轮胎充气压力成一次线性关系，采用最小二乘法拟合可以得到k1、k2与p之间的数值关系。选取多项式为

k1=α11+α12p

(2)

k2=α21+α22p

(3)

式中，k1、k2为轮胎静态径向刚度系数；p为轮胎充气压力；α11、α12、α21和α22为系数。

将式(2) 、式(3)代入式(1)，可以得到反映充气压力的轮胎静态径向刚度非线性模型，即

Fz=(α11+α12p)·Δz+(α21+α22p)·Δz2

(4)

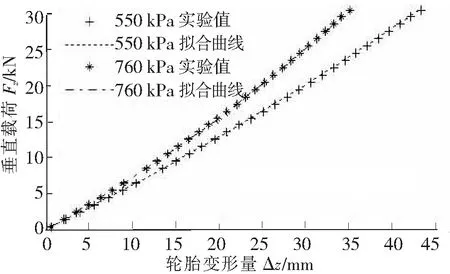
图6 静态径向刚度模型曲线与实验值对比

根据实验数据拟合可以得到，所测试轮胎的系数α11、α12、α21和α22值分别为372.339 5 N·mm-1、0.385 6 N·mm-1·p-1、-4.836 1 N·mm-2和0.013 9 N·mm-2·p-1。

选取550 kPa和760 kPa两个压力状态验证所建模型的准确性，静态径向刚度模型曲线与实验测试值对比如图6所示。从图6可以看出，所建立的轮胎静态径向刚度非线性模型与实测结果吻合。表明该静态模型可用于轮胎力学和车辆动力学的计算中。

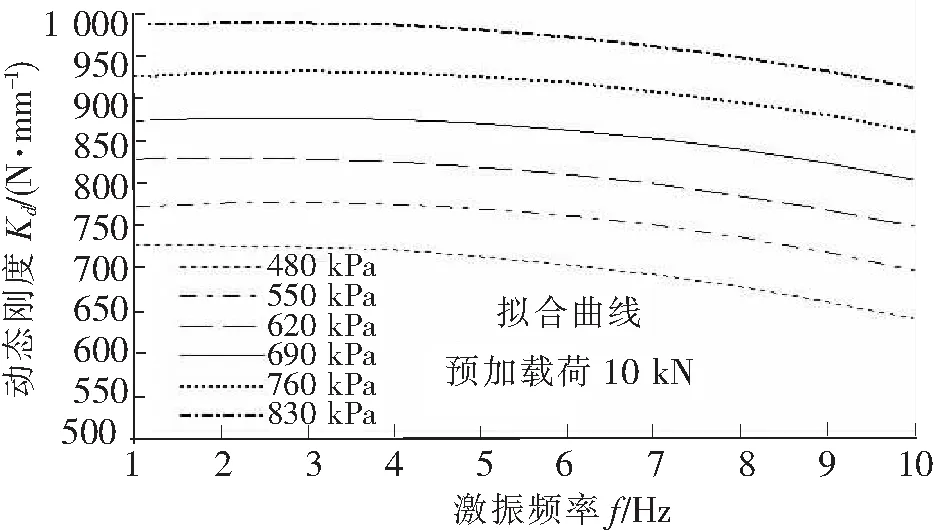
图7 动态径向刚度随激振频率与充气压力的变化关系

2.2 动态径向刚度模型的建立

在建立动态径向刚度非线性模型时，主要考虑激励频率对轮胎径向刚度的影响。对不同充气压力状态的轮胎，各取1.0～10.0 Hz之间的 10个频率进行激振测试。对所有动态实验测试的数据均采用最小二乘法进行拟合处理，得到轮胎动态径向刚度随激振频率与充气压力的变化关系，如图7所示。通过分析发现，动态径向刚度值与激振频率间存在二次非线性关系。

为了获得轮胎的动态径向刚度值和振动频率之间的数值关系，采用二次多项式(5)进行拟合

Kd=α0+α1f+α2f2

(5)

式中，Kd为动态径向刚度；α0、α1和α2为系数；f为正弦激振频率。根据实验测试结果，进行分析计算得到α0、α1和α2的具体数值，如表2所示。

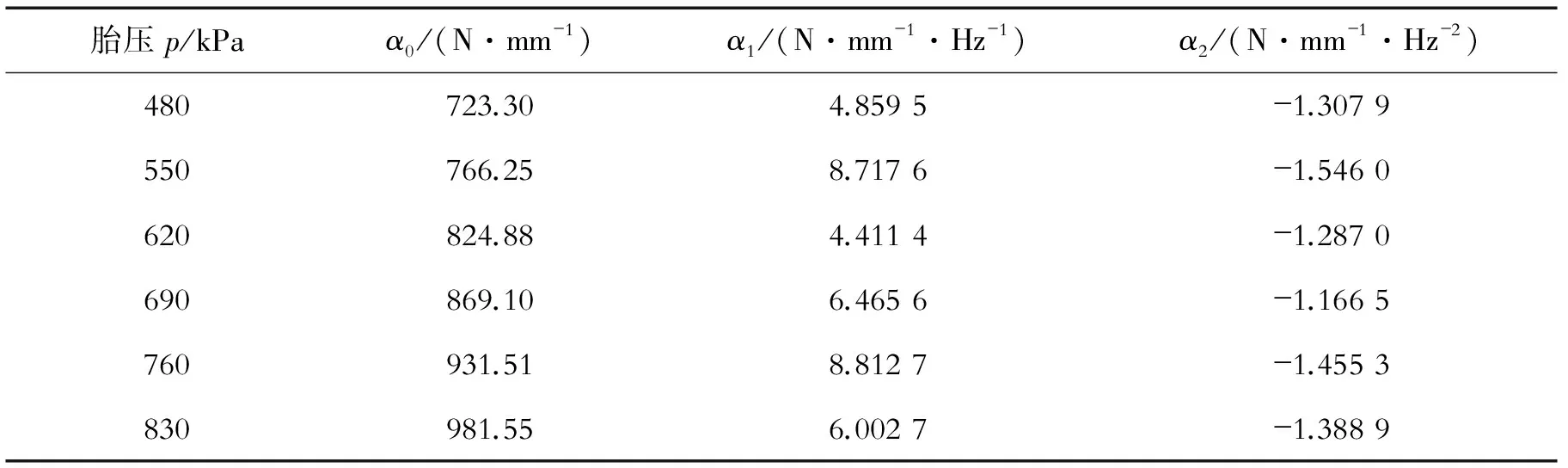
表2 轮胎动态径向刚度系数

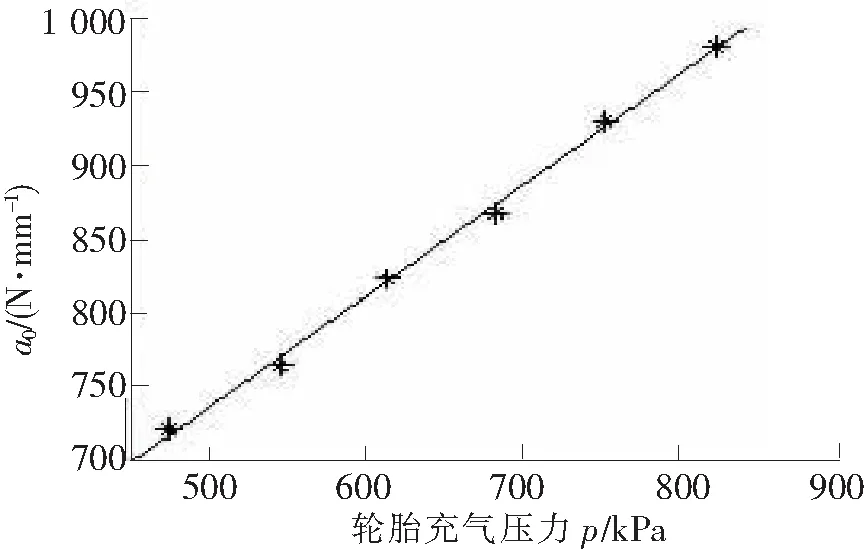
图8 α0值随轮胎充气压力的变化

分析表2中的数据可以发现α1和α2值随轮胎充气压力变化无明显规律，α0值随轮胎充气压力的升高呈线性增长趋势，如图8所示。为了更准确地表达系数α0值随轮胎充气压力p的变化关系，可用一次多项式拟合得到二者之间的数值关系，即

α0=α0d+α1dp

(6)

式中，α0d、α1d为系数。

将式(6)代入式(5)，可以得到反映充气压力和振动频率的轮胎动态径向刚度非线性模型，即

kd=α0d+α1dp+α1f+α2f2

(7)

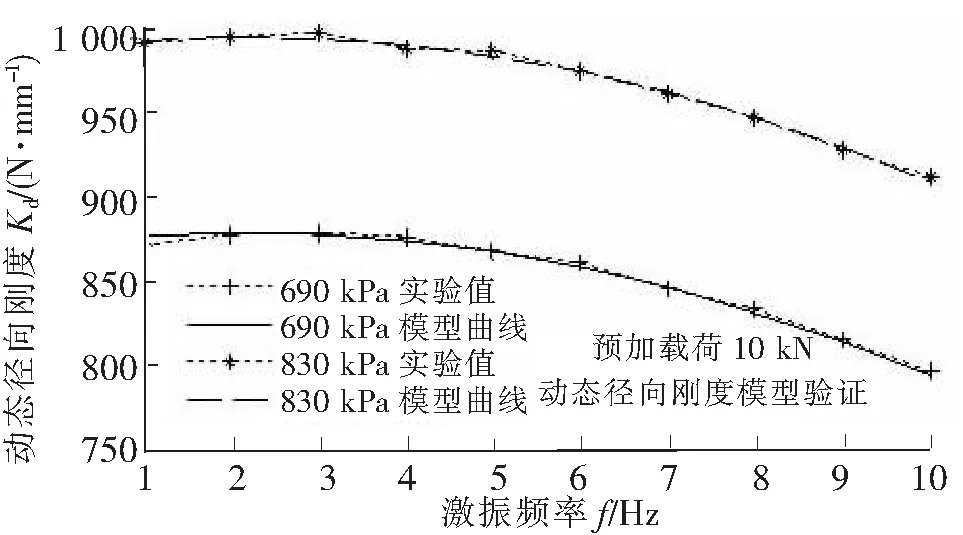
图9 动态径向刚度模型曲线与实验值对比

根据实验数据拟合可得，所测试10.00R20子午轮胎的系数α0d、α1d值分别为359.852 6 N·mm-1、0.747 4 N·mm-1·p-1。

选取690 kPa和830 kPa两个压力状态验证所建模型的准确性，动态径向刚度模型曲线与实验测试值对比如图9。从图9可以看出，所建立的轮胎动态径向刚度非线性模型与实测结果吻合。表明该动态模型可用于轮胎力学和车辆动力学的计算中。

3 结论

通过对重型车用10.00R20子午轮胎进行静态和动态径向刚度实验研究，揭示了轮胎径向刚度与轮胎变形量、充气压力和振动频率之间的非线性关系，并发现振动频率对轮胎径向刚度力的迟滞特性有影响。根据静态和动态实验测试结果，分别建立了考虑轮胎变形量、充气压力等因素的静态径向刚度非线性模型和考虑轮胎变形量、充气压力及振动频率等因素的动态径向刚度非线性模型。为轮胎力学和车辆系统动力学研究中轮胎刚度模型的建立奠定了基础。

参 考 文 献

[1]辛振祥,邓涛,王伟.现代轮胎结构设计[M].北京:化学工业出版社,2011: 1-2.

[2]王伟,燕山.带花纹轮胎静负荷试验与仿真分析[J].橡胶工业,2014,2:107-110.

[3]庄继德.汽车轮胎学[M].北京:北京理工大学出版社,1996: 273-320.

[4]陈栋华,靳晓雄.轮胎刚度和阻尼非线性模型的解析研究[J].中国机械工程学报,2004,2(4):408-412.

[5]胡林,谷正气,黄晶,等.30.00R51子午线轮胎刚度仿真[J].系统仿真学报,2008,8:2210-2214.

[6]聂信天,史立新,顾浩,等.农用轮胎径向刚度和阻尼系数试验研究[J].南京农业大学学报,2011,34(5):139-143.

[7]Reza N Jazar. Vehicle dynamics theory and application[M]. 2nd ed. New York: Springer Science,2014:103-107.

[8]范院琴,徐伟,韩群,等.随机激励下一类含分数阶阻尼的轮胎的振动响应[J].应用数学和力学,2014(12):1330-1340.

[9]喻凡,林逸.汽车系统动力学[M].北京:机械工业出版社,2005:58-63.