新型有轨电车整体道床路基顶面动态回弹模量预估方法
(国家开发银行河北省分行,河北 石家庄 050051)
0 引言
新型有轨电车采用整体道床,较传统有轨电车具有运行噪音低、运输效率高等优势,较城市公交车具有效率高、能耗低、排放少等优势,是现代城市公共交通系统的重要组成部分。自20世纪90年代欧洲、美国、日本、澳大利亚等国家开始将新型有轨电车应用于城市公共交通体系,21世纪初期我国开始新型有轨电车的建设,目前已在上海、苏州、大连、珠海等城市建设了新型有轨电车,与地铁、公交车等传统公共交通系统共同组建了新的公共交通系统。目前,采用整体道床的高速铁路路基设计已经引入了动模量指标Evd,考虑到有轨电车多需要与两边道路协同设计,本研究认为将已应用于公路设计的路基顶面动态回弹模量指标引入新型有轨电车整体道床路基设计具有重要意义。但是如何通过预估有轨电车路基顶面动态回弹模量来合理设计路基结构是亟需解决的问题[1-2]。
1 预估方法与流程
1.1 预估方法
基于有轨电车整体道床路基各层位动态回弹模量预估方程,由层状弹性体系理论,根据路基弯沉等效原则,计算路基顶面当量动态回弹模量。路基顶面当量动态回弹模量预估涉及以下主要技术问题:
(1)路基各层位动态回弹模量预估。依据各路基材料动态回弹模量预估模型,结合路基各层位应力状态、湿度与压实状态,预估有轨电车整体道床路基各层位动态回弹模量。有轨电车整体道床路基主要包括级配碎石、水泥稳定碎石、石灰处治土与素土4种材料。水泥稳定碎石较普通散粒体材料模量高、刚度大,可按照路面材料回弹模量试验方法测试其回弹模量。级配碎石、石灰处治土与素土可通过动态回弹模量预估模型计算。
(2)路基顶面弯沉计算。以弯沉等效原则计算路基顶面当量动态回弹模量,依据层状弹性体系理论计算多层结构体系的路基顶面弯沉,当满足与路基顶面基准弯沉值误差后,以路基顶面基准弯沉值所对应的路基当量动态回弹模量值作为路基顶面当量动态回弹模量。机车一组转向架与轨道共有4个接触面,所对应路基顶面范围形成一个弯沉盆,其弯沉最大点在转向架中心所对应位置。通过对静、动荷载下路基顶面弯沉值的分析,每组轮对中心处的弯沉也可达到最大弯沉值的97%以上[3],因此为了简化计算量,可选单组取轮对中心所对应的路基顶面作为弯沉计算点。有轨电车整体道床路基典型断面通常包括三层:级配碎石层(水泥稳定碎石层)、石灰处治土层与素土层(或复合地基层),因此可采用三层弹性体系计算理论进行计算。
1.2 预估流程
综合考虑路基各结构层的应力状态、湿度、压实度影响的路基顶面当量动态回弹模量计算的流程,如图1所示,其实施过程主要包括两个阶段。
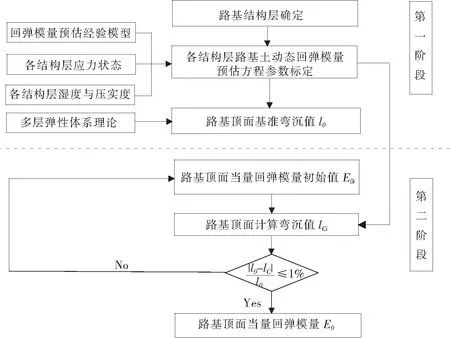
图1 路基顶面当量动态回弹模量预估流程
第一阶段:
(1)依据设计资料,确定路基各结构层所采用材料,厚度与设计压实度;通过现场试验或湿度预估,确定各层位路基土含水率;通过数值分析方法或理论求解得出各结构层应力状态。
(2)以路基土动态回弹模量本构经验模型预估方程为基础,对各结构层路基土响应本构模型中的参数进行标定,并依据上步得到的应力状态、含水率与压实度进行各结构层动态回弹模量预估;若路基结构中包括水泥稳定碎石层,则采用水泥稳定碎石结构的设计回弹模量,不需对其进行预估。
(3)依据上步预估的各结构层回弹模量值,通过多层层状弹性体系理论计算路基顶面基准弯沉值(l0)。
第二阶段:
在均质弹性半无限空间体上施加相同形式与级位的静态荷载,反复调整该均质体的回弹模量,计算路基顶弯沉值,经过多次试算,直至路基顶计算弯沉与第一阶段的路基顶基准弯沉之间的差异满足预先设定的熟练精度为止(本文要求精度达到1%),此时的调整值即为所求的路基顶面当量动态回弹模量。
2 当量动态回弹模量预估的力学模型与分析方法
2.1 空间坐标系与基本假设
对有轨电车整体道床路基而言,上部的换填层、水泥稳定碎石层与处治土层均视为路基结构。若将其简化为层状弹性体系进行计算,可将土基上部的换填层、水泥稳定碎石层与处治土层等视为弹性层状结构,将土基部分视为弹性半无限空间体。将对有轨电车整体道床路基结构简化为层状弹性体系后应符合以下4项基本假设:
(1)各结构层均为线弹性、完全均匀、各向同性、完全连续材料;
(2)自然应力状态为零,即在外部荷载作用之前,结构内无初始应力;
(3)整个结构变形符合小变形原则;
(4)土基无穷远处的应力、应变与位移均为零。
有轨电车整体道床路基结构简化为层状弹性体系后,在水平面方向无限延伸,在垂直方向向下无限延伸,因此宜采用z轴向下的柱面坐标系建立方程求解,采用右手定则。
2.2 荷载表达式
有轨电车路基结构多采用如下形式:级配碎石+石灰处治土+素土(或复合地基)。路基结构各层位模量与厚度均会对路基顶面力学响应构成影响,通过数值分析平台分析多工况组合条件下荷载作用点所对应的路基顶面竖向应力。数值分析模型如图2所示。
该分析模型中轨道、道床板、支承板、碎石层与处治土层采用弹性模型,各土层采用Mohr-Coulomb模型模拟。
分析中使用隐式动态分析步(Dynamic,Implicit),分析时长0.2 s,矩形荷载。将轨道结构阻尼比ζ设定为0.05,计算相应的Rayleigh阻尼比例系数,结果为α=2.532×10-5,β=3.082×10-3。路基结构阻尼比ζ取0.10,其中α=5.065×10-5,β=6.163×10-3。
图3是荷载分别作用于板中与横跨两板时动荷载作用下路基顶竖向应力分布形态,选取竖向应力最大的分析步结果。当荷载作用于板中时,动荷载作用下路基顶竖向应力在荷载作用下区域呈近似圆形分布;当荷载横跨两板时,由于板边挠度大,在板边所对应的路基顶面出现应力集中。如果不考虑板边应力集中影响,路基顶面的应力可近似为圆形。路基顶部的圆形应力也不是均布的,中心大,四周小,呈近似球形。为了表达方便,将路基顶部竖向应力简化为均布圆形应力,如式(1)所示。

图3 不同工况条件下路基顶竖向应力分布

(1)
式中,σ为等效应力集度;δ为路基顶面应力当量半径。δ可通过式(2)计算。
(2)
式中,P为作用在车轮上的荷载;p为路基顶面当量竖向应力。作用在车轮上的荷载P为列车轴载的一半。路基顶面当量竖向应力p的确定成为路基顶面应力当量半径δ确定的关键。
各结构层模量与厚度取值范围列于表1中,共选取36种路基结构组合,进行路基顶面应力分析,采用动态应力分析,动应力系数k=2.6[3-4],电车轴重取12.5 t。图4为荷载分别作用于板中、板边与横跨两板时各工况条件下荷载作用区域路基顶面最大动应力的分布情况,横轴代表最大应力所在区间,纵轴代表各应力区间的路基结构组合数量。
图4中数据表明各荷位下路基顶面的最大动应力呈正态分布,因此荷载作用于板中、板边与横跨两板时路基顶面最大动应力分别选取42.5 kPa,57.5 kPa与125.0 kPa。前文分析已表明每个轮轨接触面下路基顶面竖向应力以近似“碗状”分布,而方程(1)将路基顶面应力简化为一均布圆形应力,因此应将路基顶面最大动应力予以折减,作为路基顶面的均布应力。本文取折减系数为0.7[3],因此荷载作用于板中、板边与横跨两板时路基顶面当量竖向应力p分别为29.75 kPa,40.25 kPa与87.5 kPa。依据式(2),将路基顶面应力当量半径δ列于表2。
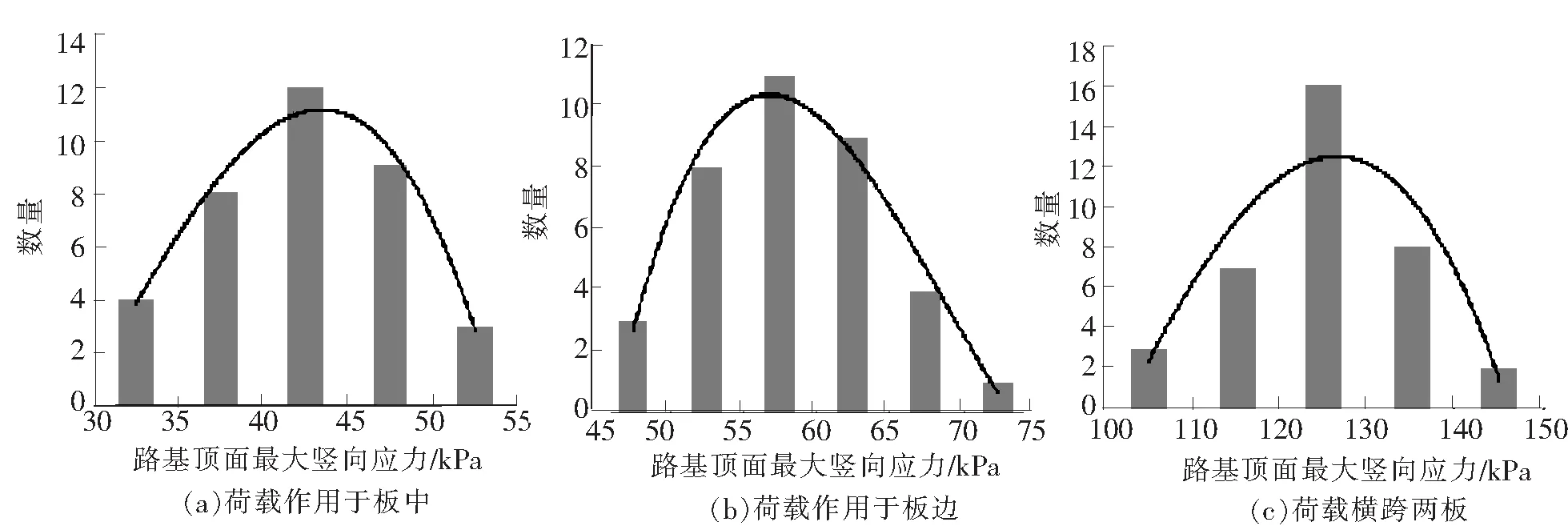
图4 荷载作用区域路基顶面最大动应力分布

表1 有轨电车整体道床路基各层位参数范围

表2 路基顶面当量竖向应力与竖向应力当量半径
2.3 力学分析方法
在道路工程中,已经比较成熟地使用层状弹性理论来计算路基路面中的力学问题。层状弹性体系可用来计算路基顶的弯沉值,因此依据弯沉等效原则计算路基顶当量动态回弹模量。有轨电车整体道床路基结构中土基上多铺设级配碎石层(或水泥稳定碎石层)与石灰处治土层两层换填与改良土层,因此可将有轨电车整体道床路基结构视为三层弹性体系模型,并假定层间完全连续,采用圆形轴对称荷载。
3 算例分析
3.1 各层位路基填料动态回弹模量预估
3.1.1 土基动态回弹模量计算
选取某有轨电车项目试验段的复合地基和天然地基断面进行分析,复合地基断面结构如图5示。该段土基强度较差,采用了旋喷桩进行地基处理,桩径800 mm,桩长4.0 m,横向桩间距2.4 m,纵向桩垂直间距2.1 m,近似等边三角形布桩。桩体无侧限抗压强度≥1.0 MPa。石灰处治土采用8%~10%的石灰掺入比。级配碎石最大粒径小于60 mm,不均匀系数大于15,0.02 mm以下颗粒小于3%。石灰处治土层与级配碎石层的压实度均为96%。
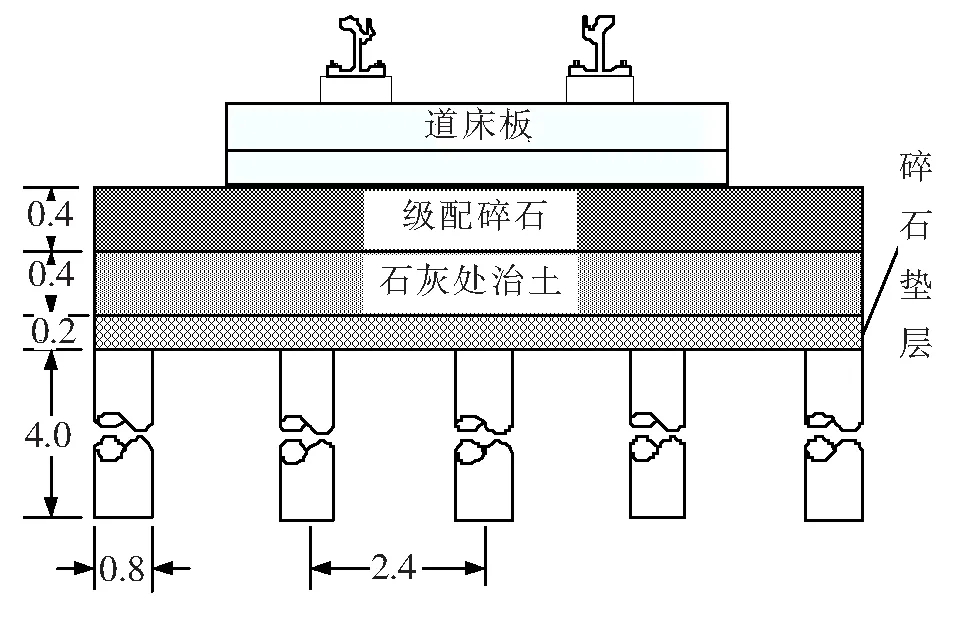
图5 复合地基段路基结构示意图(单位:m)
将复合地基等效为均质土基,方可通过本文提供的方法进行路基顶面动态回弹模量预估。可通过复合地基的承载板试验得到其静态回弹模量,再根据动态回弹模量与静态回弹模量之间的经验关系,计算复合地基动态回弹模量。
本文通过桩的面积置换率计算复合地基动态回弹模量。
Ecd=mEpd+(1-m)Esd
(3)
式中,m为桩土面积置换率;Ecd为复合地基动态回弹模量;Epd为桩体动态回弹模量;Esd为桩间土动态回弹模量。
通过现场承载板试验获取桩体与桩间土回弹模量。桩体的现场承载板试验结果表明桩的弹性模量为646 MPa,依据水泥材料动态回弹模量与静态回弹模量的关系,将桩体的动态回弹模量取为646 MPa。桩间土的承载板试验结果表明其回弹模量为36.2 MPa,依据路基土动态回弹模量与静态回弹模量的关系,将桩间土动态回弹模量取为72 MPa。从而可求得复合地基动态回弹模量Ed=129.4 MPa。研究结果表明动应力作用下路基工作区深度可达到8 m[3],因此土基部分动态回弹模量应综合复合地基动态模量与下覆土层动态回弹模量,考虑到各层位应力状态对土基顶面当量动态回弹模量的影响,本研究采用地基设计规范[5]中地基压缩模量当量值的计算方法。
(4)
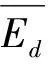
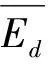
3.1.2 石灰处治土层动态回弹模量预估
石灰处治土试样含水率为16.5%,比最佳含水率高1.1%,试样干密度1.64 kg/cm3,压实度为96.5%。选取压实度为96%时,wopt工况下三参数模型,可得本算例中最佳含水率下石灰处治土层动态回弹模量预估方程为[3]
(5)
依据数值分析结果,动应力系数k=2.6时石灰处治土层竖向应力可取为45.0 kPa,水平应力为17.0 kPa,从而可求得体应力θ=79 kPa,八面体应力τoct=13.20 kPa。此工况下最佳含水率时石灰处治土的动态回弹模量MR(opt)=128.38 MPa。

3.1.3 级配碎石层动态回弹模量预估
级配碎石层动态回弹模量预估同样借用既有研究成果,罗志刚[6]通过对3种不同压实度与含水率下的级配碎石动三轴测试结果,建立了级配碎石材料动态回弹模量的三参数预估模型,如式(6)所示,三参数采用回归结果的中值。
(6)
依据数值分析结果,动应力系数k=2.6时级配碎石层竖向应力可取为80.0 kPa,水平应力为35.0 kPa,从而可求得体应力θ=150.0 kPa,八面体应力τoct=21.21 kPa。此工况下级配碎石层的动态回弹模量MR=216.51 MPa。
3.2 路基顶面弯沉与当量动态回弹模量
3.2.1 基准弯沉值
根据路基结构与各层动态回弹模量预估结果,路基结构各层模量与厚度如表3所示。
依据前文提供的有轨电车整体道床路基顶面当量竖向应力预估方法,计算路基顶面基准弯沉值,结果如表4所示。

表3 路基结构计算参数

表4 路基顶面基准弯沉值
3.2.2 计算弯沉值与路基顶面当量动态回弹模量
将路基等效为一层均质材料,依据表4中的路基顶面当量竖向应力与当量半径,分别计算弯沉值与当量动态回弹模量的关系,经过试算,路基当量动态回弹模量以4 MPa为步长进行搜索。各工况下路基当量动态回弹模量结果列于表5与表6。

表5 复合地基中路基顶面计算弯沉与当量动态回弹模量

表6 天然地基中路基顶面计算弯沉与当量动态回弹模量
3.3 结果验证
本次测试采用CARL BRO HWD对路基顶面进行弯沉测试。荷载板直径30 cm,设9个弯沉传感器,距荷载中心位置2.5 m范围内可以任意调节位置。可认为路基顶面应力当量半径δ=15 cm,可求得路基顶面当量竖向动应力p=884.6 kPa,因此将测试动应力设定为900 kPa。
在试验段复合地基段与天然地基段的级配碎石层顶面各选取5个试验点进行HWD测试。表7为各试验点路基顶面弯沉测试结果,并依据弯沉等效原则反算各测点的当量动态回弹模量。

表7 路基顶面动态回弹模量测试结果
表7中复合地基与天然地基两种工况下路基顶面动态回弹模量测试结果的平预估均值与各测点的误差均在10%以内,因此采用表7中提供的模量均值分别作为复合地基与天然地基之上路基顶面当量动态回弹模量值。表8为路基顶面当量动态回弹模量预估值与原位测试结果的对比分析。
表8中的数据表明路基顶面当量动态回弹模量的预估值与实测值的误差均在10%以内;荷载横跨两板时的预估值均大于实测值,荷载位于板中与板边时预估值小于实测值。荷载位于板边时的预估值略小于实测值,出于工程安全考虑,可选取荷载位于板边时的预估值作为路基顶面当量动态回弹模量值。
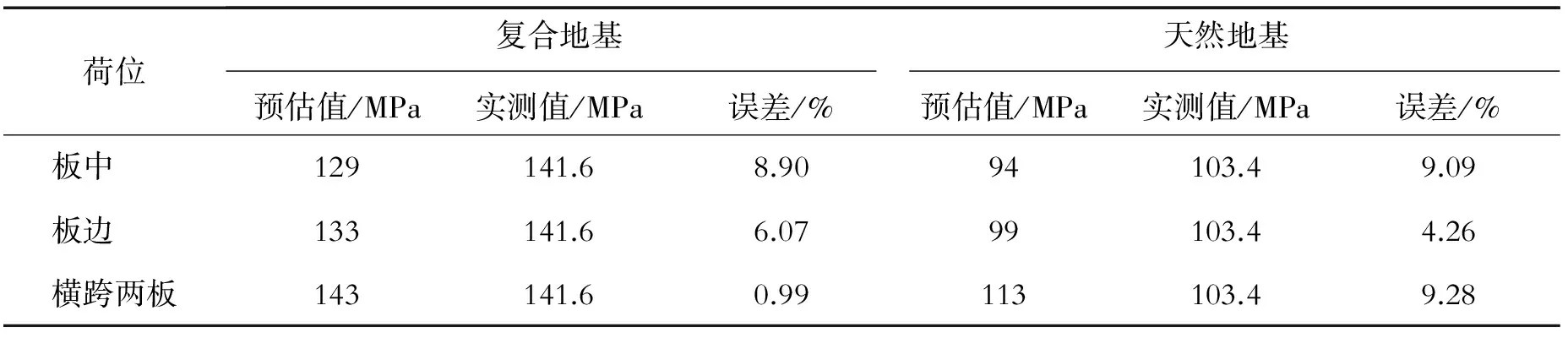
表8 路基顶面当量动态回弹模量预估值与实测值对比
4 结论
本研究基于新型有轨电车整体道床路基结构特点,建立了一套用于预估路基顶面动态回弹模量的方法,主要有以下成果:
(1)基于有轨电车整体道床路基各层位动态回弹模量预估方程,由层状弹性体系理论,根据路基弯沉等效原则建立了预估流程;
(2)通过数值分析研究了各工况下有轨电车整体道床路基顶面的应力分布特征,路基顶部应力可等效为圆形分布,且当转向架横跨两个道床板时路基顶部应力最大;
(3)以某软土地区有轨电车项目为案例,预估结果与现场测试结果误差在10%以内,因此本研究提供的预估方法是有效的。
参 考 文 献
[1]Leighton K, Gillespy M. Nottingham express transit line 1: geometrical aspects [J]. Transport, 2005, 159(2): 63-68.
[2]Lamaran G, Derdas Menon. Evaluation of dynamic load on railtrack sleepers based on vehicle-track modeling and analysis[J].International Journal of Structural Stability and Dynamics, 2002, 2(3): 355-374.
[3]王硕. 有轨电车整体道床路基力学响应与设计参数研究[D]. 上海: 同济大学, 2013.
[4] 杨宏印,陈志军,彭旭民. 基于子区间的车-线-桥振动不平顺影响分析[J]. 石家庄铁道大学学报:自然科学版,2016,29(2):6-11.
[5]中华人民共和国建设部. GB 50007—2011 建筑地基基础设计规范[S]. 北京: 中国建筑工业出版社, 2011.
[6]罗志刚. 路基与粒料层动态模量参数研究[D]. 上海: 同济大学, 2007.

