双渠道闭环供应链博弈模型的复杂性分析
张 芳,马小林
(天津工业大学 理学院,天津 300387)
随着经济全球化和技术的高速发展,再制造对经济和环境的可持续发展的影响日益显著[1].同时,由于严格的环境法律法规和资源短缺的意识增强,越来越多的公司对回收的旧产品进行了再制造[2].因此闭环供应链被广泛应用于生产和学术研究中[3-4].美国国际贸易委员会数据表明:美国再制造产品总销售额从2009年的373亿美元增加到2011年的430亿美元[5].张宏伟等[6]以及马祖军等[7]研究了逆向物流的优化设计模型.Xu等[8]研究了带有参考价格的闭环供应链,分析了参考价格对各个成员利益的影响.
近年来,随着电子商务的迅猛发展,网上购物越来越盛行,成千上万的供应商,例如:IBM、思科和耐克,在开通传统渠道的同时,在网上又开通了直销渠道.Mathieu等[9]研究了在零售渠道、直销渠道和双渠道下的利润影响,研究表明:双渠道将会达到最优利润;Kurata等[10]研究了直销渠道和间接渠道以及品牌店竞争下的定价决策;此外,关于供应链长期动态博弈模型很多学者做了大量的研究.Guo等[11]建立了零售商回收的闭环供应链博弈模型,分析了参数对系统的影响,从经济学的角度解释了复杂的非线性动态博弈行为;Zhang等[12]研究了带有关切公平的零售商的双渠道供应链的动态博弈,通过数值模拟,分析了公平关切系数和决策参数对系统的影响,研究了系统的分岔图以及最大Lyapunov指数和混沌吸引子等复杂的动力学行为.
本文在上述相关文献的研究基础之上,建立了一个考虑参考价格影响的双渠道闭环供应链博弈模型,研究了在制造商主导回收下的静态和动态博弈模型,分析了渠道偏好参数以及参考价格系数对定价的影响,并利用分岔图、最大Lyapunov指数[13]以及混沌吸引子分析了该模型的动力学行为.
1 问题描述与假设
本文研究了一个由单一制造商和单一零售商组成的考虑参考价格的双渠道闭环供应链.假设制造商生产某种产品,同时开设直销渠道销售,将产品以批发价批发给零售商.顾客既可以通过零售渠道也可以通过直销渠道去购买产品.同时,产品在市场上会被回收.考虑制造商回收情形,并且在制造商主导下进行Stackelberg价格博弈.供应链结构如图1所示.
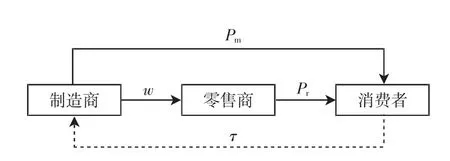
图1 供应链系统Fig.1 Dual-channel closed loop supply chain systerm
图1中:w为单位批发价格;Pr为单位零售价格;Pm为单位直销价格;τ为回收率.
制造商开设直销渠道销售产品,直销渠道和传统渠道在一个具有潜在市场大小的普通市场上竞争.本文考虑了消费者参考价格的影响[14],则零售渠道和直销渠道的需求函数[15]分别为:
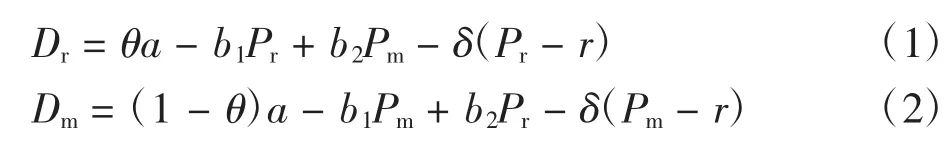
式中:Dr表示零售渠道中消费者的需求;Dm表示直销渠道中消费者的需求.参数α代表了潜在的市场规模.θ(0<θ<1)代表顾客对零售渠道忠诚度.则θα=ar表示倾向零售渠道的顾客数,而(1-θ)α=am表示倾向于直销渠道的顾客数.b1(b1>0)表示Dr和Dm的价格弹性系数.交叉价格敏感度b2(b2>0)反映了产品通过2个渠道销售互为替代品的程度.设b1>b2即自身价格作用大于交叉价格作用.r为消费者的参考价格,δ是参考价格系数,它反映了参考价格对需求的影响,较高的δ值表示消费者对当前价和参考价的差异非常敏感.此外,根据实际情况,参数应满足:(i)Cm,Cr< w 由此推出: 式中:Cm为使用原材料制造新产品的单位成本;Cr为使用回收材料再制造新产品的单位成本;Δ为单位节约成本,即:Δ=Cm-Cr. 本文关于闭环供应链做如下一些假设: ①市场中回收生产的再制造产品和原材料制成的新产品具有统一的销售价. ②参考价格大于用原材料生产新产品的成本.即r>Cm. ③回收再制造的单位成本小于原材料生产新产品的单位成本.即Cr<Cm. ④单位节约成本大于传递价格,传递价格大于单位处理成本.即A ⑤回收率借鉴文献[16],即是回收率,B是尺度参数,I是回收投资. 本模型中,制造商具有领导地位,零售商是跟从者,二者形成Stackelberg博弈.同时,制造商主导回收过程,其首先决策批发价w,直销价Pm和回收率τ,然后零售商决策零售价Pr. 制造商的利润函数为: 零售商的利润函数为: 则零售商对制造商制定的价格的反应函数为: 其中,A为处理回收产品的单位成本. 其中当满足: 时,Hessian矩阵是负定的,故制造商的利润函数是凹的并且存在唯一的最优解.求得均衡解为: 式中: 将 Pm、w、τ和 Pr代入式(5)和式(6)即可算出制造商的最优利润函数πMm和零售商的最优利润函数πMr. 取参数 b1=6、b2=3、Δ =10、A=5、B=1 000、Cm=20、r=25、ar=200θ、am=200·(1- θ)、b=7、δ=0.5 进行数值模拟.分析渠道参数 θ对 Pm、Pr、w、τ以及制造商利润πMm和零售商利润πMr的影响,如图2所示. 由图2可知,当渠道忠诚度θ在0.3和0.5之间时,批发价w小于Pm、Pr,在实际生产中有意义.此时,零售商的利润随着θ的增加而增加,而回收率和制造商的利润随着θ的增加反而减小.这是因为随着渠道忠诚度θ的增大,倾向零售渠道的顾客增多而直销渠道的顾客减少,使得零售商的利润逐渐增加而制造商的利润有所损失.制造商制造商可以从提高服务质量、加大广告力度等方面去提高直销渠道的顾客数,使其获得较大收益. 取参数 b1=6、b2=3、Δ =10、A=5、B=1 000、θ=0.45、Cm=20、r=25、ar=90、am=110 进行数值模拟.分析渠道参数 δ对 Pm、Pr、w、τ以及制造商利润 πMm和零售商利润的影响,如图3所示. 由图3 可知,Pm、w、τ和制造商利润均随着参考价格系数δ的增加而减小,回收率τ和零售商利润则随着参考价格系数的增加而增加.这说明在一个对参考价格和实际价格差异比较敏感的市场里,价格竞争明显,制造商利润会受到影响. 图2 渠道忠诚度对价格、回收率和利润的影响Fig.2 Effects of channel parameter on price,collection rate and profit 通过以上分析可以看出,随着渠道忠诚度参数和参考价格系数的增加,零售商利润均是逐渐增加的,制造商利润则是降低的,2个参数对回收率的影响刚好相反.所以,在生产实际中,制造商应该采取措施增加直销渠道的渠道偏好,同时也要考虑参考价格系数对系统的影响. 图3 参考价格系数对价格、回收率和利润的影响Fig.3 Effects of reference price parameter on price,collection rate and profit 本文认为决策者在价格决策过程中不可能完全理性,基于已有的文献和相关经济理论,认为决策者在决策过程中是有限理性的,其对应的价格调整表达式为: 式中:αi>0为企业的价格调整速度,为正值;为边际利润,可从式(10)、式(11)和式(12)中获得. 公式(14)给出了制造商的决策,决策变量直接与α1、α2和 α3有关.零售商的决策变量 w(t)直接与 Pm(t)有关.即: 由公式(14)确定的系统的8个均衡点如下: 式中:EM是 Nash均衡点;w、Pm和Pr分别为(10) 式、(11)式和(13)式. 命题:在条件(3)、(4)和(9)下,所有的边界均衡点Ei(i=1,2,…,7)均是不稳定的. 证明:系统的雅可比矩阵为: 其中: 对于均衡点Ei(i=1,2,3),它们对应的其中一个特征值分别为: 由于 b1> b2,得到|r1|> 1,|r2|> 1,|r3|> 1,故均衡点Ei(i=1,2,3)是不稳定的. 对于均衡点E4,其雅可比矩阵一个特征值为: 由(9)式以及 E6中的 w6大于零,可证|r4|> 1,故均衡点E4不稳定. 对于均衡点E5,其雅可比矩阵的一个特征值为: 由式(3)和式(4)可得: 由此可得出:|r5|>1,故均衡点E5不稳定. 对于均衡点E6,其雅可比矩阵的一个特征值为: 由(9)式以及 Pm大于零,可得:|r6|> 1,故均衡点E6不稳定. 对于均衡点E7,其雅可比矩阵的一个特征值为: 由式(9)、2(b22-(b1+δ)2)< 0 以及均衡解 w 大于零,可得:|r7|>1,故均衡点E7不稳定.故系统在Ei(i=1,2,…,7)均不稳定.证毕. 利用Jury条件[17-18]可以研究Stackelberg均衡点EM的局部稳定性.雅可比矩阵的特征多项式为: 同时,其对应的Jury条件下的局部稳定性为: 下面针对动态Stackelberg博弈模型进行数值模拟,研究调整参数对系统稳定域以及产品价格的影响.基于实际的竞争情况,本文选择了一些参数值.令α=20;θ=0.45;b1=6;b2=3;δ=0.5;Δ =10;A=5;B=1 000;Cm=50;r=25;此时算出均衡点为 w=25.29,Pm=26.35,τ=0.1,Pr=26.61. (1)系统的稳定域.图4给出了均衡点EM的稳定区域.可以看出稳定区域大致为α1<0.012,α2<0.06,α3<0.01,.当参数属于稳定区域时,均衡解是局部吸引的.较高的调整速度会使系统离开稳定区域. 图4 系统的稳定域Fig.4 The stable region of the system (2)调整参数αi(i=1,2,3)对系统的影响.由于调整参数αi对系统影响的分岔图以及最大Lyapunov指数图类似,下面以调整参数α2对系统影响为例.系统的分岔图、最大Lyapunov指数图以及混沌吸引子图如图5所示. 图 5(a)、(b)展示了 α1=0.02,α3=0.002,α2介于0 到 0.01 之间时,Pm、Pr、w、τ随 α2变化的分岔图,图 5(c)为对应的最大的Lyapunov指数图. 由图 5(a)、(b)、(c)可以看出:当 α2<0.006 31时,系统处于稳定状态,此时,w=25.29,Pm=26.35,τ=0.1,Pr=26.61;当 α2=0.006 31 时,系统开始进入分岔期,随着α2的增加,当α2=0.008 04时,系统进入2倍分岔周期,然后4倍分岔、8倍分岔等等,α2=0.008 41时,Lyapunov指数大于零,系统进入混沌,此时价格波动剧烈,对整个市场不利.图 5(d)展示了公式(14)的另一个动力学特征,即混沌吸引子. 图5 系统的分岔图、最大Lyapunov指数图以及混沌吸引子图Fig.5 Bifurcation diagrams,the largest Lyapunov exponent and Chaos attractor of system 本文考虑了一个由单一制造商和单一零售商组成的带有参考价格的双渠道闭环供应链的定价决策问题.建立了制造商主导回收的静态和动态博弈模型,并通过数值模拟分别分析了在静态模型下渠道忠诚度以及参考价格系数对定价决策的影响.利用稳定域图、分岔图、最大Lyapunov指数图以及混沌吸引子研究了动态模型的复杂动力学性质.结果表明:在静态模型中,制造商利润均随着渠道忠诚度和参考价格系数的增大而减小,而零售商利润随着它们的增大而增大;在动态重复博弈中,过快的调整速度会使系统进入混沌,当调整参数α2过大时,系统进入不稳定,价格波动明显,市场情况不可预测.因此,参与者应当考虑适当的调整参数,使市场进入有序竞争.对于在零售商主导下渠道参数与参考价格系数对系统的影响,以及多个制造商或者多个零售商组成的复杂闭环供应链系统等问题的研究是未来进一步研究的方向. [1]MUKHOPADHYAY S K,MA H.Joint procurement and production decisions in remanufacturing under quality and demand uncertainty[J].International Journal of Production Economics,2009,120(1):5-17. [2]高丽峰,赵丹丹.基于循环经济理念下的电子废弃物再利用[J].中国环保产业,2004(12):20-22.GAO L F,ZHAO D D.Reuse of electronic wastes based on circular economy [J].China Environmental Protection Industry,2004(12):20-22(in Chinese). [3]候光明,李存金.管理博弈论[M].北京:北京理工大学出版社,2005.HOU G M,LI C J.Game Theory of Management[M].Beijing:Beijing Institute of Technology Press,2005(in Chinese). [4]冯·诺依曼,摩根斯坦恩.博弈论与经济行为 [M].上海:生活·读书·新知三联书店,2004.JOHN V N,OSKAR M.Theory of Games and Economic Behavior[M].Shanghai:SDX Joint Publishing Company,2004(in Chinese). [5]BULMUS S C,ZHU S X,TEUNTER R.Competition for cores in remanufacturing [J].European Journal of Operational Research,2014,233(1):105-113. [6]金晨泽,张宏伟.基于低成本的逆向物流回收策略探讨[J].铁道运输与经济,2005,27(11):19-21.JIN C Z,ZHANG H W.Discussion on the take-back strategy of reverse logistics based on low cost[J].Railway Transport and Economy,2005,27(11):19-21(in Chinese). [7]马祖军,代颖.产品回收逆向物流网络优化设计模型[J].管理工程学报,2005,19(4):114-117.MA Z J,DAI Y,Optimization model for reverse logistics network design for product recovery[J].Journal of Industrial Engineering Management,2005,19(4):114-117(in Chinese). [8]XU J,LIU N.Research on closed loop supply chain with reference price effect[J].Journal of Intelligent Manufacturing,2017,28(1):51-64. [9]MATHIEU R G,LEVARY R.Hybrid retail:Integrating ecommerce and physical stores [J].Industrial Management,2000,42(5):6-13. [10]KURATA H,YAO D Q,LIU J J.Pricing policies under direct vs.indirect channel competition and national vs.store brand competition[J].European Journal of Operational Research,2007,180(1):262-281. [11]GUO Y,MA J.Research on game model and complexity of retailer collecting and selling in closed-loop supply chain[J].Applied Mathematical Modelling,2013,37(7):5047-5058. [12]ZHANG F,MA J.Research on the complex features about a dual-channel supply chain with a fair caring retailer[J].Communications in Nonlinear Science&Numerical Simulation,2016,30(1/2/3):151-167. [13]张家忠.非线性动力系统的运动稳定性、分岔理论及应用[M].西安:西安交通大学出版社,2010.ZHANG J Z.Stability and Bifurcation of Nonlinear Dynamic Systems and Their Applications[M].Xi′an:Xi′an Jiaotong University Press,2010.(in Chinese) [14]FINE C H,PORTEUS E L.Dynamic process improvement[J].Operations Research,1987,37(4):580-591. [15]KOPALLE P K,ASSUNCAO J L.Asymmetric reference price effects and dynamic pricing policies [J].Marketing Science,1996,15(1):60-85. [16]YAO D Q,YUE X,LIU J.Vertical cost information sharing in a supply chain with value-adding retailers[J].Omega,2008,36(5):838-851. [17]罗昌,贾素玲.基于系统动力学的供应链稳定性判据研究[J].计算机集成制造系统,2007,13(9):1762-1767.LUO C,JIA S L.Stability criterion of supply chain based on system dynamics[J].Computer Integrated Manufacturing Systems.2007,13(9):1762-1767(in Chinese). [18]PUU T.Attractors,bifurcations,and chaos:Nonlinear phenomena in economics[J].Springer Berlin,2000,75(2):186-189.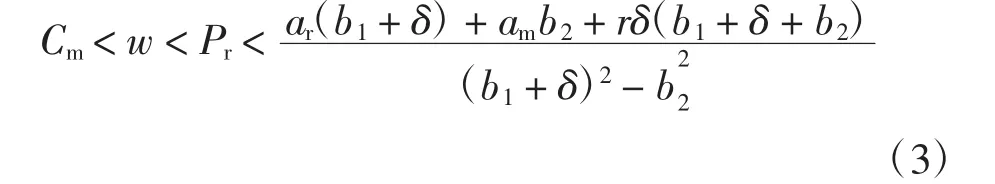
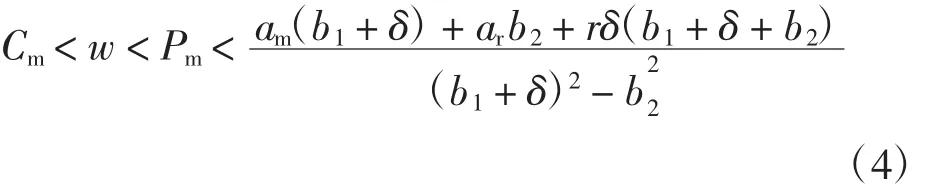
2 静态模型
2.1 模型建立
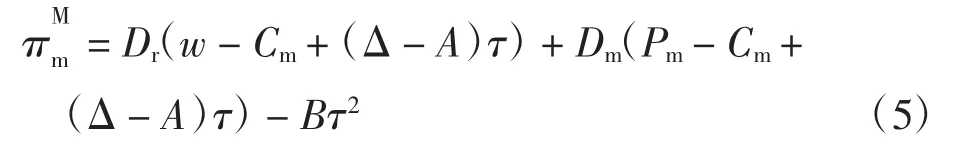

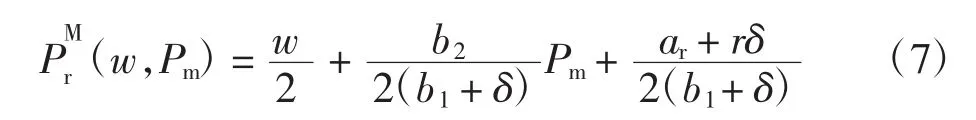
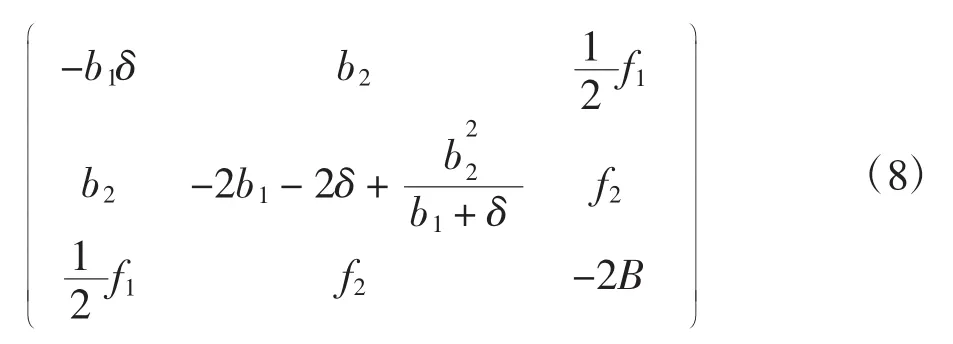
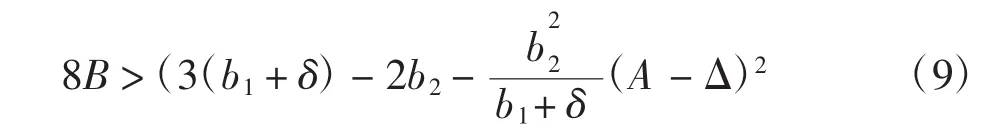
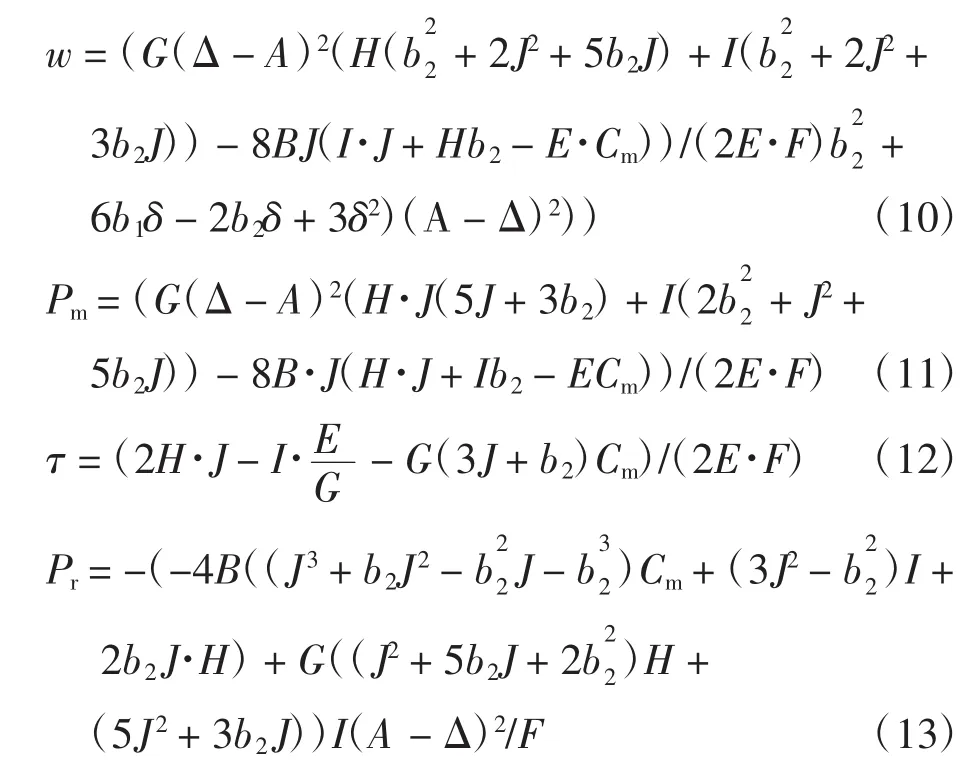
2.2 渠道忠诚度θ对系统的影响
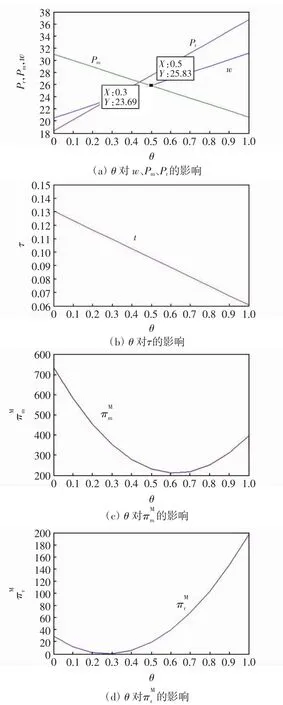
2.3 参考价格系数δ对系统的影响
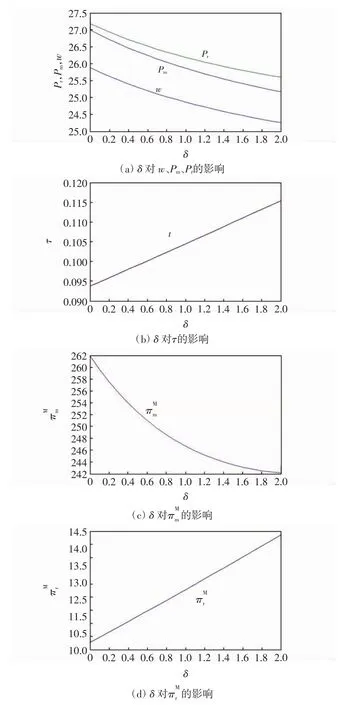
3 相应的动力学价格调整模型
3.1 模型建立
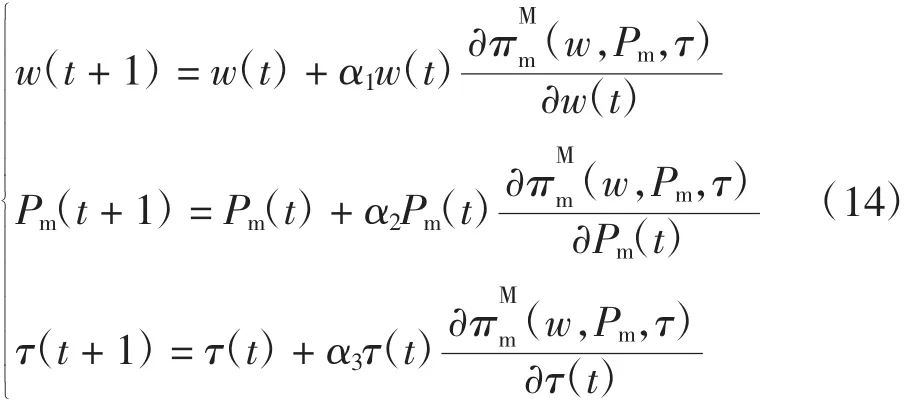
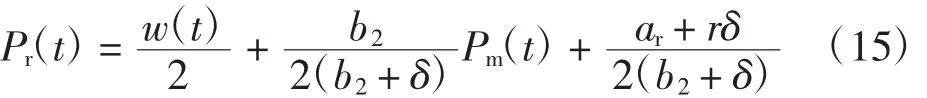
3.2 系统的稳定性分析

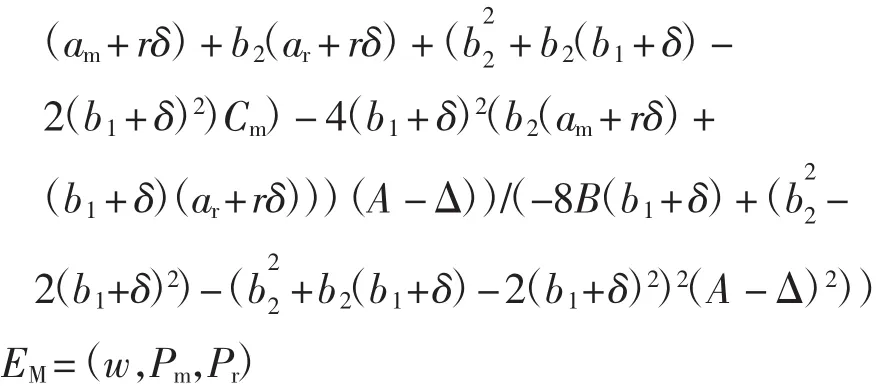
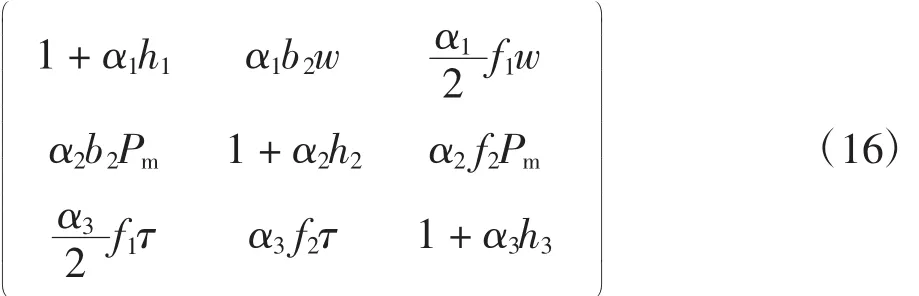
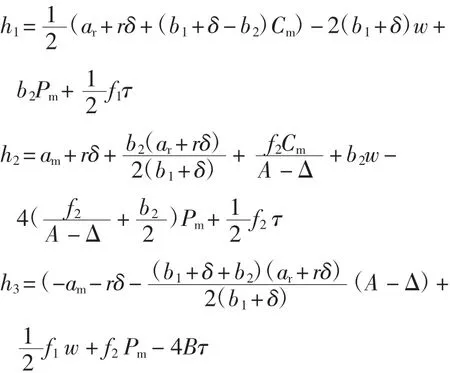
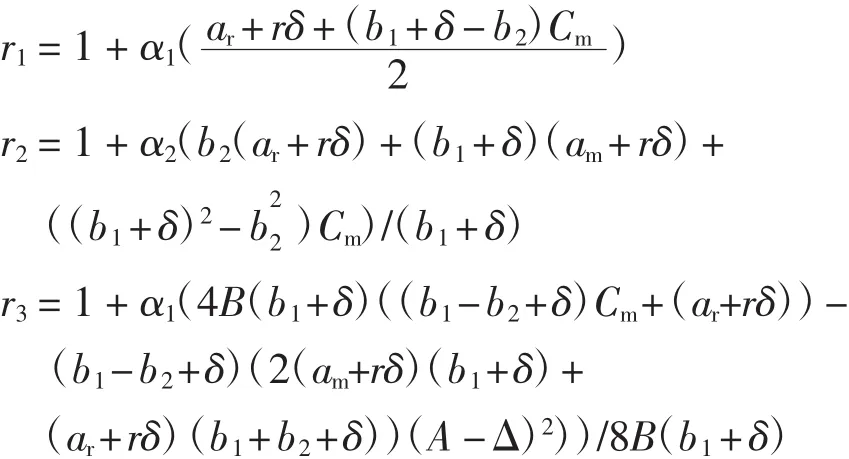
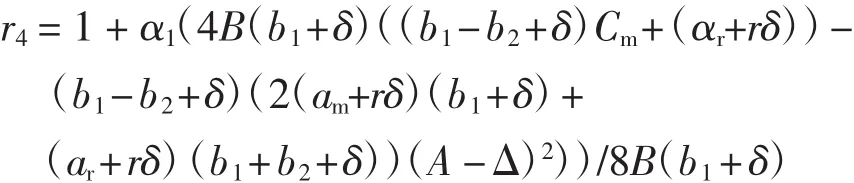
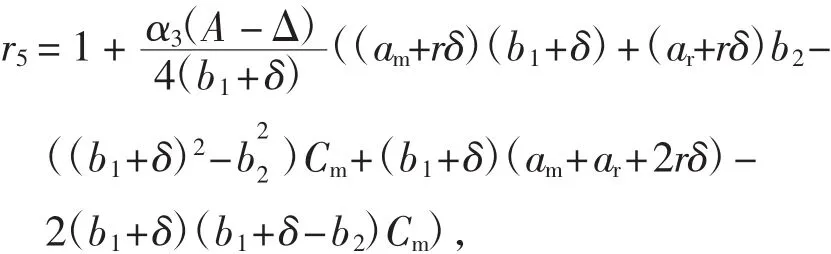
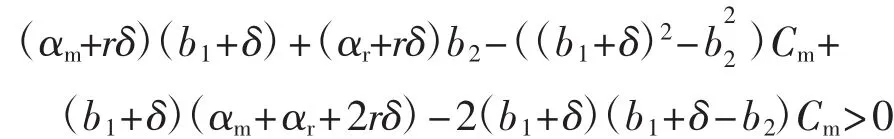
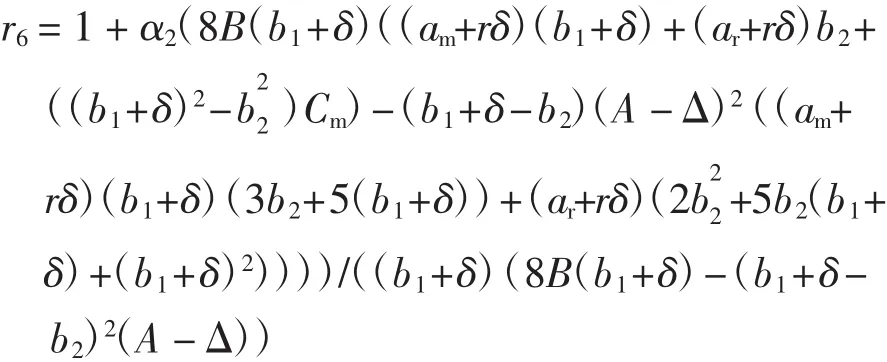
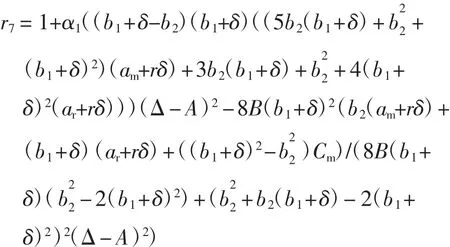
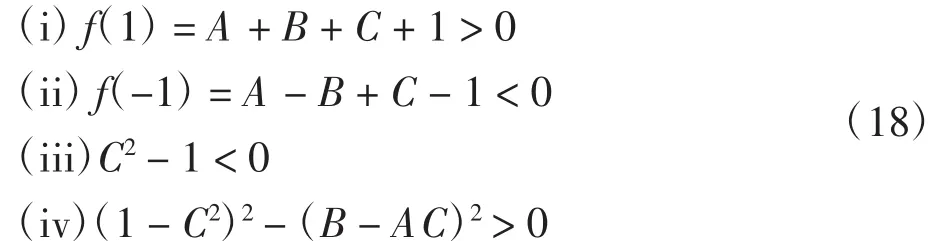
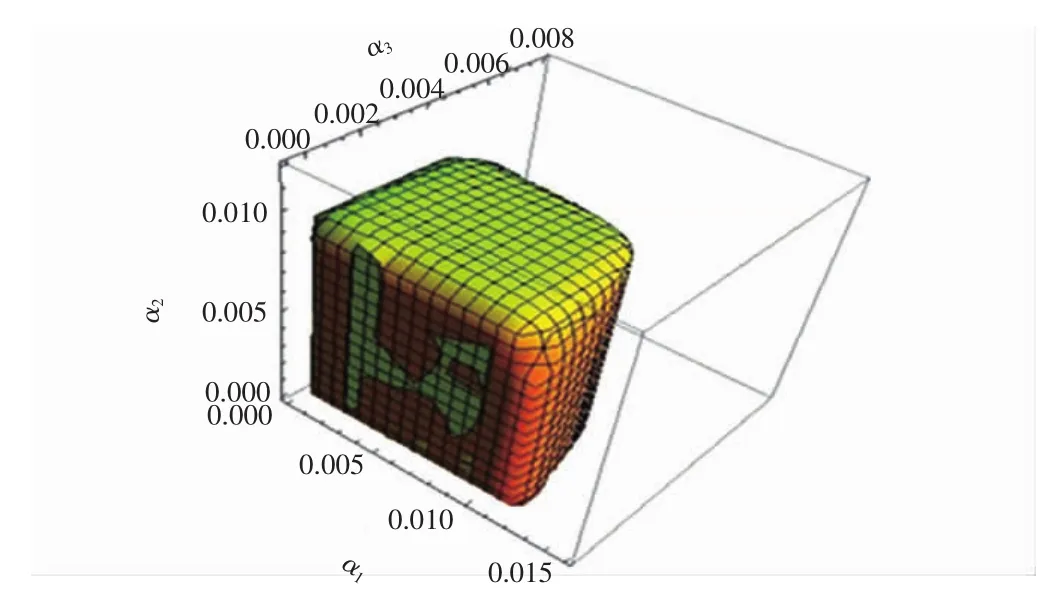
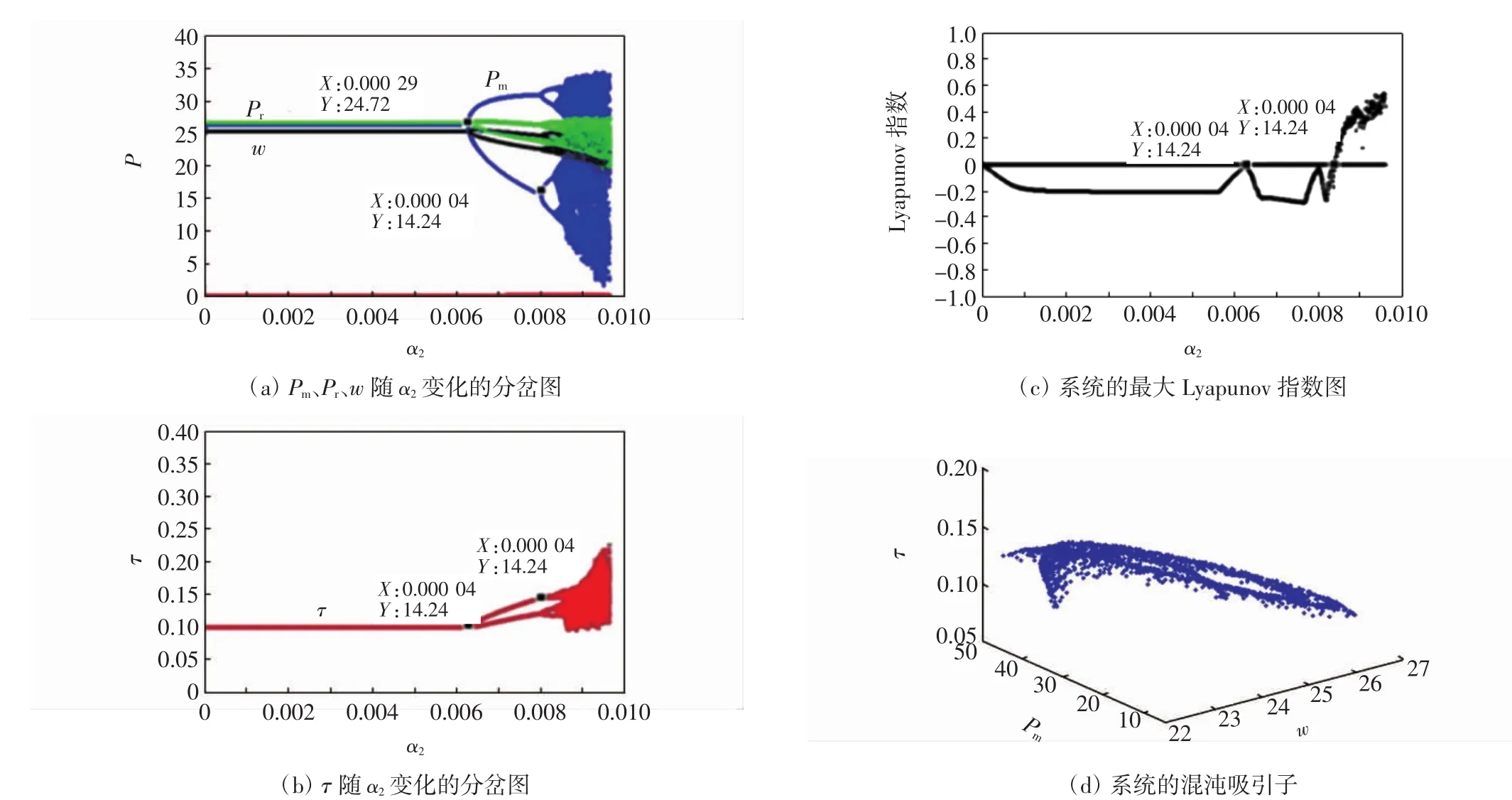
3.3 动态数值模拟
4结语

