基于几何主动轮廓模型的图像分割方法

张荣华，吴 益，王 亨，肖 磊，唐劲天

（1.天津工业大学 电气工程与自动化学院，天津 300387；2.清华大学工程物理系，北京 100084；3.清华大学 粒子技术与辐射成像教育部重点实验室，北京 100084）

变分水平集是几何主动轮廓模型的重要代表，自Osher等[1]在研究速度与曲率相关的曲线演化时提出以来，因其诸多优点被广大学者研究，在图像处理领域尤其是医学图像分割方面被广泛改进和运用.该方法基本思想是用高维曲面来映射低维曲线，曲线轮廓演化的方程式被隐含表示，所以水平集函数的演化方程能够从高阶闭合曲面或曲线的演化方程中推导出来，内嵌的演化曲面或曲线就是其零水平集.因此，只需要设计零水平集，然后就可以计算出演化曲面或曲线的结果[2-4].该方法的最大优点就是不依赖主动轮廓的参数化，而且能够合理地处理拓扑结构发生变化的曲线.

传统水平集方法必须定期地初始化水平集函数作为符号距离函数，以此来缩小迭代过程带来的计算错误，Li等[5]引入一个内部能量项到能量泛函来纠正水平集函数与符号距离函数的偏差，提出一种无需初始化的演化方法.在此基础上，Xu[6]又加入新的符号距离函数正则项来纠正偏差，提出距离正则水平集.近些年，许多其他有价值的分割模型也结合变分水平集相继被提出.CV模型将目标边缘终止函数消除掉，是一种无需边界的主动轮廓模型[7].Gao等[8]用局部鲁棒统计（LRSS）来对抗图像噪声，并利用稀疏场算法让能量项的计算更加高效.Brox等[9]针对灰度不均匀分割图像提出分段常值模型（PS）.Li等[10-11]提出局部二值方法（LBF），该模型将图像的局部信息嵌入其中，能够分割出灰度不均匀的血管图像.

上述方法聚焦于水平集演化方向和速度的控制，忽略了终止函数对分割最终效果的影响，不能在尖角边界终止演化，对初始演化区域敏感并且不能正确识别多个目标.本文构造了新的终止函数和自适应性选择系数，提出一种新的边缘主动轮廓模型的自适应算法：一方面，图像信息用来决定水平集函数的演化方向，因而演化结果不依赖于初始轮廓的位置；另一方面，外部能量项与终止速度函数相互独立，收敛速度也得到提高.

1 水平集原理

考虑曲线在有界区域R2内跟随时间变化，设定C（x，y，t），x，y∈R2是一条闭合曲线；水平集函数设为U（x，y，t）∶R2× [0，t]→R，将曲线嵌入让水平集函数变为隐函数Uc（x，y，t）=d，d∈R为常数.基于曲线演化理论有：

式中：F为速度函数，决定曲线C上每个点的演化速度；N为曲线的单位内法向量，具体表示为N=-ΔU/|ΔU|，Δ为梯度算子.

结合（1）式对隐函数求其关于t的微分有如下结果：

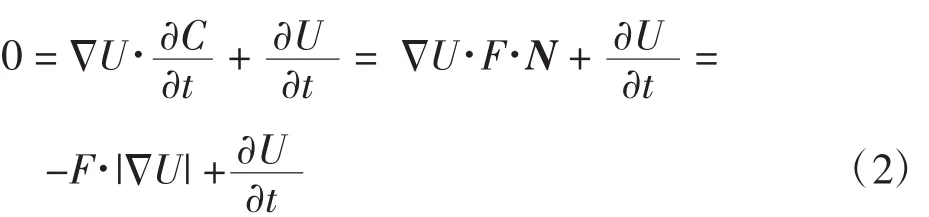
因此 C（x，y，t）的演变转变为水平集函数的偏微分方程可表示为：

图1所示为水平集演化思想的示意图.图1中：曲面代表水平集函数U（x，y，t）；黑色加粗曲线表示演变的轮廓曲线C.

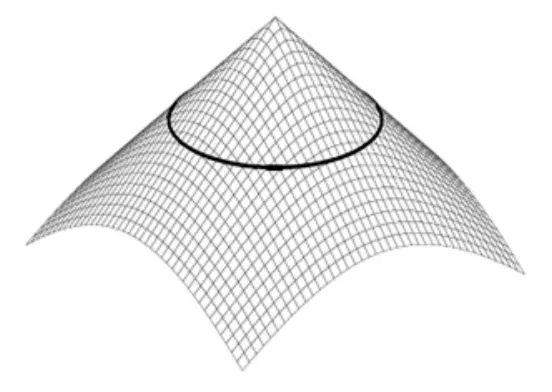
图1 水平集思想示意图Fig.1 Illustration of level set principle

曲线的演变过程其实是曲线上不同力的作用过程，也即能量的作用.分割目标区域趋于能量最小而存在，所以，建立能量模型然后按照一定的约束条件求能量最小，即可分割出目标轮廓[12].水平集方法用于图像分割的几何主动轮廓模型的一般过程可以概括为：

Step1：图像输入与预处理；

Step2：建立能量模型后利用变分法取得Euler-Lagrange方程；

Step3：利用水平集方法获取曲线演化的偏微分方程；

Step4：设定初始水平集后选取PDE数值算法进行迭代运算；

Step5：利用终止函数判断是否满足停止演化条件，不满足条件时继续迭代；

Step6：演化终止，输出水平集函数，得到最终的分割曲线.

2 本文模型

2.1 边缘终止函数

在图像分割时，主动轮廓模型可被分为基于边界模型[3，10-12]和基于区域的模型[4，13-15]两大类.基于边界的水平集利用图像的梯度来构建边缘检测函数，以此来终止曲线演化，勾画出目标边界.通常，速度终止函数有如下两类选取方法：

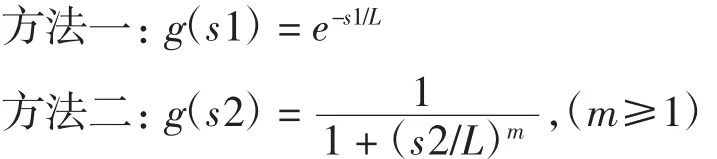
式中表示对图像进行高斯滤波预处理.图2反映了多种速度终止函数的特征.

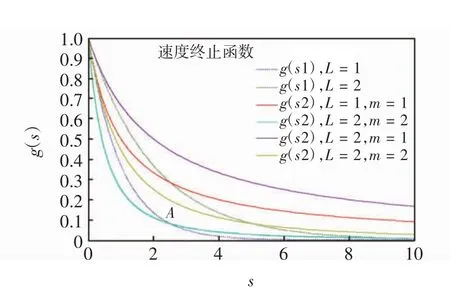
图2 多种速度终止函数特征曲线Fig.2 Variety function characteristic curves of velocity termination

图2中，L=1时，g（s1）在A点以后对梯度变化很敏感，快速趋近于0，g（s2）则相对平缓.L=2时，g（s1）和g（s2）在s值较小区域下降缓慢，这将影响曲线收敛的时间，降低分割的速度.对于L的选取，方法不一，如将梯度取绝对平均值、将绝对偏差取中值、引入Canny噪声估计[13]等，但所有方法都是以分离目标边缘和噪声作为出发点.当分割目标处于低信噪比图像中时，很难区分梯度的变化是由噪声还是边缘信息产生，因此难以权衡噪声的平滑和弱边缘信息的保留.综合以上分析，一般情况下：

由式（4）可知，函数g在演化过程中依赖图像信息，梯度的模值起决定作用，在目标边界时g接近0.弱边界时，此边缘检测函数往往不连续并且不完全等于0，因此不能充分地终止水平集演化.再者，g始终为正值，曲线朝单一方向收敛，目标点一旦泄露便不能返回.

因此，本文提出L函数化的方案，将其定义为：

式中：I（x，y）为图像灰度信息；m为分割前输入参数；h1、h2为2个卷积函数的商，分别近似于图像在高斯窗内和在高斯窗外的平均灰度值.具体定义为：

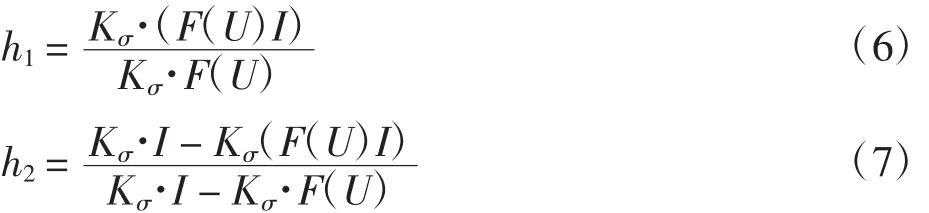
式中：F 是修改的 Heaviside 函数[11，14]；Kσ为高斯核，核函数中的尺度参数σ＞0，两者的函数表达式为：

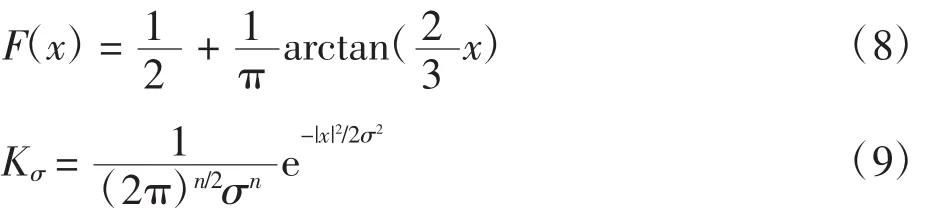
因此得出如下新的边缘终止函数：

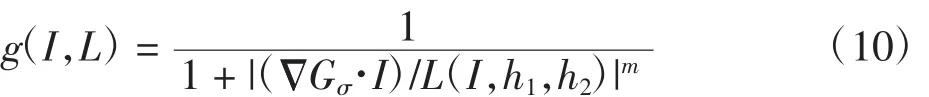
当水平集演化到目标边界时，式（5）中分子分母均接近于1，故L（I，h1，h2）≈1.此时，|（ΔGσ·I）|很大，由式（10）可知，g函数值近似零，能量模型陷入极小；当目标点被水平集包含但离边界距离比较远时，式（5）中分子项远大于 1，而分母项近似 1，所以 L（I，h1，h2）＞＞1，g（I，L）≈1，模型能量未达极小，水平集在非目标边界处继续演化.

2.2 可变权重系数

可变权重系数ω（I）能让算法根据图像信息自动的改变演化方向，所以零水平集自适应演化，克服了对初始位置敏感的缺陷.可变权重系数ω（I）定义为：

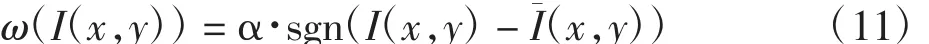
式中：I（x，y）为图像的灰度值；I（x，y）为反向灰度值；sgn（·）象征一个符号函数；α为大于零的常数.

主动轮廓在目标区域外时，I（x，y）-I（x，y）＞ 0，可变权重系数引导水平集向目标区域内靠近，相反，轮廓位于区域内时，I（x，y）-I（x，y）＜ 0，ω（I）则引导水平集朝区域外演化.换句话说，零水平集能自适应的决定演化方向，有利于摆脱初始位置的干扰.与此同时，α的不同取值也能在复杂图像分割时，对不同轮廓层起识别作用.

2.3 数值描述与算法实现

基于以上讨论，本文模型的能量泛函为：

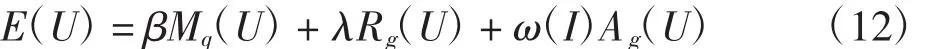
式中：β＞0为常数；Mq（U）用来修正水平集函数的内部结构，定量的描述水平集函数与符号距离函数的偏差程度，定义如式（13）.其中的能量密度函数 q（s）按照（14）式分段选取，为保证演化过程中符号距离特性只在零水平集附近成立，q（s）在s=1和s=0时最小，避免水平集受困于局部最优解，水平集演化的稳定性和有效性得到保证.

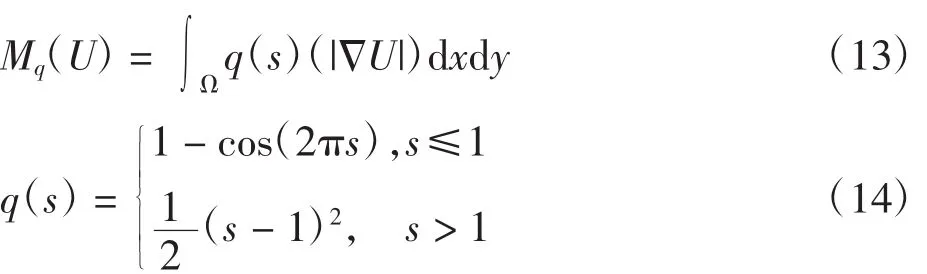
水平集定义在区域Ω内，初始水平集U0（x，y）设置为分段常值函数[17]，若点在区域内等于-2，否则设为2.能量函数中Rg（U）的用来计算轮廓的曲线积分，Ag（U）表示区域Ω-U={x ∶U（x）＜ 0}的加权面积.

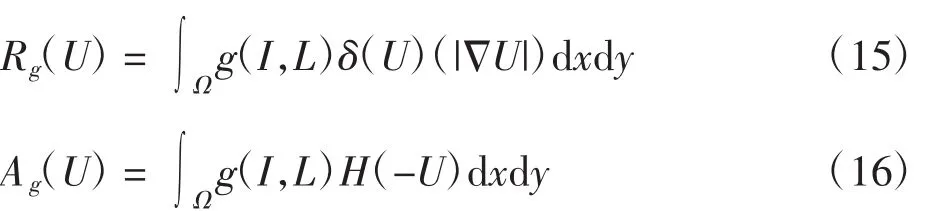
水平集方法实现过程中，平滑函数δ（x）和H（x）分别用（17）式和（18）式中的Dirac函数和Heaviside函数[15]来代替，式中H′（x）=δ（x）.

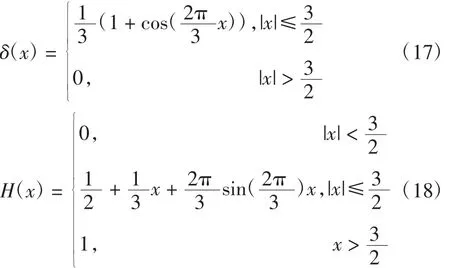
运用变分方法，E（U）的最小值可以由如下的梯度流方程式[16]算出：

当t=0时，U（x，y，0）表示初始水平集U0（x，y），∂E（U）/∂U代表求E（U）的导数.结合上述推导，偏微分方程式转化为：

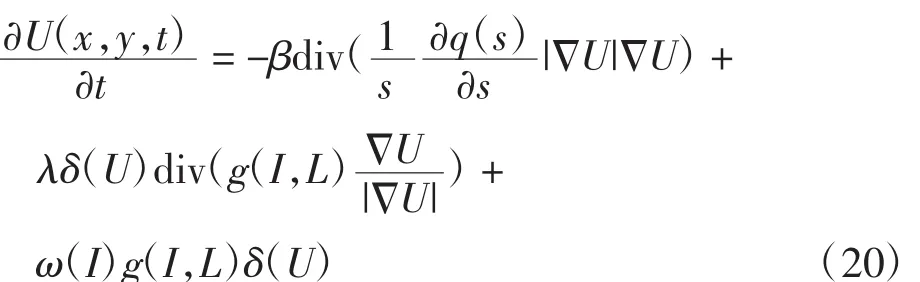
上述偏微分方程综合诺伊曼边界条件和初始轮廓曲线得出最终结果，式（20）的离散方式采用有限中心差分方法.

3 实验与应用

为验证算法的准确性和有效性，本文选取各具特征的图像进行试验，试验平台为i5-2320CPU，64bit win7企业版操作系统的计算机，编程环境为R2013a版本的MATLAB.

对比Li等[5-6]的算法，本文描述的几何主动轮廓水平集方法有其优点.首先，演化方向可以根据图像信息自行决定，不再是单向的演化；然后，带尖角的目标区域、多目标对象（灰度值可不同）均能被准确识别；再者，也能分割带内腔的多目标并且计算时间短.

不同初始区域分割多目标如图3所示.为证明算法的自适应演化能力，图3中初始区域和目标轮廓分别内部包含、相互交叉和互不相交.选用不同的初始位置对多目标图像进行分割实验，该算法不仅能准确、快速地识别出所有目标，而且自适应的决定演化方向.然而，用Li等[5-6]提出的方法即使迭代580次（迭代次数已超过本文算法的3倍），变分水平集仍不能正确的收敛，出现漏分割和边界识别不准确等分割结果不理想的现象.另外，它的分割方法太依赖初始轮廓所在的位置来人工调整曲线的演化方向.本文提出的算法用更少的迭代时间得到了有效的分割结果，证明了算法的有效性.

选用一幅人造图像作为实验对象，该图像由3个灰度值不同的图形组成，其中有一个凹形和带封闭内腔的图形.在初始轮廓位置相同的情况下试验，结果如图4所示.从左至右依次为：初始区域、Li[5]的方法分割结果、本文分割算法结果.提出的算法不仅快速识别出外部边界和凹形目标区域，还分割出图形的内部腔体边界，但是Li[5]的方法分割效果不佳.

图3 不同初始区域分割多目标Fig.3 Multiple targets segmentation with different initial regions

图4 分割复杂的人工图像Fig.4 Segmentation of complex artificial images

尖角边界识别如图5所示.为了证明算法识别尖角边界的能力，图5中用来进行对比试验的树叶轮廓有多个尖角，仍然是相同的初始轮廓下，本文算法准确、快速地分割出目标区域的所有尖角.然而，用Li等[5]提出的方法进行试验，即使580次迭代后，尖角依然很难被识别，而且改变初始位置或者增加迭代次数继续分割也没有好转的趋势.

图5 尖角边界识别Fig.5 Recognition of sharp angle boundary

CT肝脏肿瘤识别如图6所示.为进一步验证算法的可行性，图6为将算法应用到CT图像识别人体肝脏肿瘤位置的实验结果图.由图6可知，提出的算法能够有效地识别出肿瘤位置，可用于医学图像的组织器官分割[17-18].

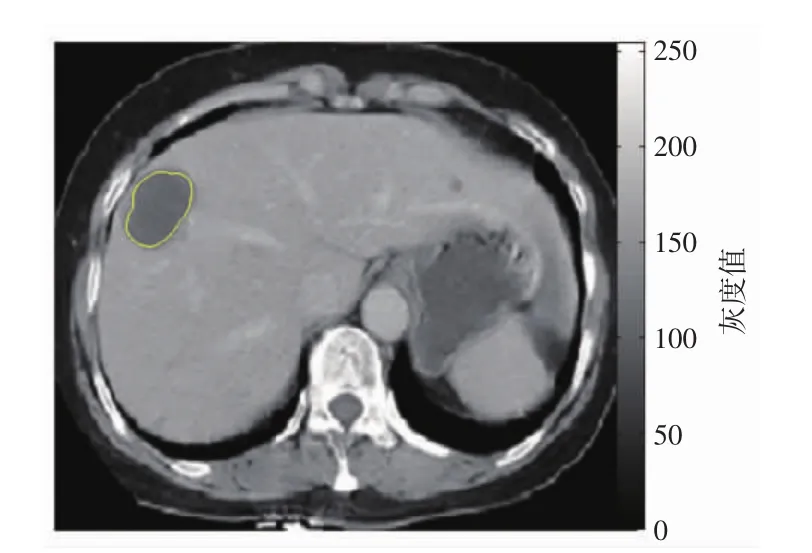
图6 CT肝脏肿瘤识别Fig.6 Recognition of CT liver tumor

算法开始前的输入参数β=1.5，λ=1.5跟Li等[5]的方法保持一致，另外2个关键输入参数m和α由实验得出，实验发现m在范围[1，2.5]取值效果较好.表1给出了以上实验图像的信息（按出现顺序标号从小到大）、分割参数的选择以及各实验的迭代次数和用时，不难看出本文提出算法的分割效率较高.

表1 本文算法分割参数及效率Tab.1 Segmentation parameters and efficiency of this algorithm

分割评价用 Jaccard（J）系数、Dice（D）系数进行综合评定.J系数和D系数是分割中基于相似度评测的常用量化标准，其值越接近1表明结果与标准相似度越高，两大系数分别定义如下：

式中：S1为标准图像轮廓的像素集合；S2为分割算法结果图的像素集合.

本文算法分割结果的量化评估如表2所示.其中图像No.1（即图3实验图像）对应的3次分割结果的评估参数均近似0.95.同时，用Li[5]的算法进行评估参数对比，图3中不同初始区域下，Li[5]等的方法J系数分 别 为 ：0.89、0.73、0.56；D系数分别为：0.90、0.76、0.61.图4和图5的对比试验中，其方法的评估系数同样低于本文方法，具体为：图4中J系数为0.72，D系数为0.75；图5中J系数为0.83，D系数为0.84.

表2 本文算法分割系数Tab.2 Segmentation coefficient of this algorithm

4 结论

为克服传统水平集方法的缺陷，促进水平集分割方法在医学图像上的应用，本文结合几何主动轮廓模型提出了一种新的改进方法.对比传统和现行的算法，该算法具有一定的优势.

（1）算法可以自我调整演化方向，让分割过程不依赖曲线所在的初始位置.

（2）算法能准确分割出多目标、尖角弱边界和凹形、带内腔图案且分割结果的J系数在0.91以上，D系数不低于0.95.最后，该算法在更为复杂的人体器官CT图像分割中也表现良好，能较好的分割出目标肿瘤轮廓.算法的准确性、快速性和可靠性得到验证.

[1]OSHER Stanley，SETHIAN James A.Fronts propagating with curvature-dependent speed：Algorithms based on Hamilton-Jacobi formulations[J].Journal of Computational Physics，1988，79（1）：12-49.

[2]KIM W，KIM C.Active contours driven by the salient edge energy model[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society，2013，22（4）：1667-1673.

[3]吕晓琪，石静，任晓颖，等．一种基于水平集的三维肝脏磁共振图像混合分割方法[J]．数据采集与处理，2015（2）：350-358.LYU X Q，SHI J，REN X Y，et al.A 3D liver hybrid magnetic resonance image segmentation method based on level set[J].Data Acquisition and Processing，2015（2）：350-358（in Chinese）.

[4]郑倩.医学图像分割方法研究及其应用[D].广州：南方医科大学，2014.ZHENG Q.Research and application of medical image segmentation method[D].Guangzhou：Southern Medical University，2014（in Chinese）.

[5]LI C，XU C，GUI C，et al.Level set evolution without re-ini－tialization：A new variational formulation[C]//Computer Vision and Pattern Recognition，2005.[s.l.]：IEEE Xplore，2005：430-436.

[6]XU C.Distance regularized level set evolution and its application to image segmentation[J].IEEE Transactions on Image Processing，2010，19（12）：3243.

[7]CHAN T F，VESE L A.Active contours without edges[J].IEEE Press，2001，10（2）：266-277.

[8]GAO Y，TANNENBAUM A，KIKINIS R.Simultaneous multiobject segmentation using local robust statistics and contour interaction[C]//Recognition Techni-ques and Applicationsin Medical Imaging.Berlin：Springer Berlin Heidelberg，2010：195-203.

[9]BROX T，CREMERS D.On the statistical interpretation of the piecewise smooth mumford-shah functional[C]//International Conference on Scale Space and Variational Methods in Computer Vision.Berlin：Springer-Verlag，2007：203-213.

[10]LI C，KAO C Y，GORE J C，et al.Implicit active contours driven by local binary fitting energy[C]//Computer Vision and Pattern Recognition，2007.[s.l.]：IEEE，2007：1-7.

[11]王茜，彭中，刘莉.一种基于自适应阈值的图像分割算法[J].北京理工大学学报，2003，23（4）：521-524.WANG Q，PENG Z，LIU L.An image segmentation algorithm based on adaptive threshold[J].Journal of Beijing Institute of Technology，2003，23（4）：521-524（in Chinese）.

[12]ZHANG K，SONG H，ZHANG L.Active contours driven by local image fitting energy[J].Pattern Recognition，2010，43（4）：1199-1206.

[13]曹武.心脏CT序列图像分割算法研究[D].北京：北京交通大学，2016.CAO W.Study of segmentation algorithms on cardiac CT sequence images[D].Beijing：Beijing Jiaotong University，2016（in Chinese）.

[14]ZHANG K，ZHANG L，ZHANG S.A variational multiphase level set approach to simultaneous segmentation and bias correction[J].IEEE International Conference on Image Processing，2010，119（5）：4105-4108.

[15]何小虎.图像分割算法研究[J].福建电脑，2014，30（8）：3-4.HE X H.Research on image segmentation algorithm[J].Fujian Computer，2014，30（8）：3-4（in Chinese）.

[16]LU S，HUANG H，LIANG P，et al.Hepatic vessel segmentation using variational level set combined with non-local robust statistics[J].MagneticResonanceImaging，2017，36：180-186.

[17]ZHENG Q，DONG E，CAO Z，et al.Active contour model driven by linear speed function for local segmentation with robust initialization and applications in MR brain images[J].Signal Processing，2014，97：117-133.

[18]HUANG J，JIAN F，WU H，et al.An improved level set method for vertebra CT image segmentation[J].Biomedical Engineering Online，2013，12（1）：48.