腔光机械系统的纠缠演化特征

闫学群，岳建林

（天津工业大学理学院，天津 300387）

随着纳米技术的高速发展，纳米结构机械系统大量涌现.近几年来，一种新兴的纳米结构系统-腔光机械系统已经引起了人们的极大研究兴趣[1].腔光机械系统是一个通过利用激光驱动腔场，使腔场成为一个共振腔，在腔中的机械振子由于受辐射光压的驱动而产生振动，使腔的长度发生改变从而改变腔模原来的频率，再通过相互调制使光场和机械振子耦合起来的系统.在过去的研究中，以光腔和机械振子为基础的研究领域都已经得到了成熟的发展.由机械振子与光腔组成的腔光机械系统在量子检测、量子信息理论研究中也显示出广阔的应用前景.例如，超高精度的位移探测[2-3]、质量探测[4]、引力波探测[5]等.Cohadon 等[6]利用一定功率激光束驱动腔模场，在激光束的驱动下通过相互调制使光学腔与机械振子耦合，在实验上成功制成这一经典系统-腔光机械系统.

量子纠缠是量子信息研究中的一种重要物理资源，为了充分利用这一资源，研究者们基于腔光机械系统做了大量的工作.例如，制备纠缠态、度量系统纠缠度和利用纠缠等[7-9].机械振子与光场之间的纠缠以及光场与机械振子之间的态转移已被做了大量的理论研究.Mancini等[10]通过一定的理论运算推导把光场量子态转移到机械振子上，从而讨论了两个机械振子之间的纠缠演化特性.Vitali等[11]设计出一种可以测量腔光机械系统中腔场和机械振子纠缠度的实验方案.机械振子不仅在纯态中具有许多有趣的纠缠演化特性，而且在混合态中也可以诱导产生多种系统之间的纠缠.Barzanjeh等[12]在腔光机械系统中制备出存在时间更长的光场纠缠态.

随着量子通信技术的快速发展，量子光机械器件在量子通讯技术方面具有潜在的应用价值.腔光机械系统对光信息具有易于储存、快速传输和长时记忆等优点[13-14].腔光机械系统不仅可以将光场中的携带的量子信息转移到机械振子上，而且也可以把机械振子中的量子态转移到腔场中，因此它可以作为一种交换器被广泛的应用到量子通信技术中.Stannigel等[15-16]提出一种以机械振子为交换器来实现高保真度的腔场与机械振子之间量子态转移.Tian等[17]通过绝热的条件下调节腔场与机械振子之间的耦合强度，从而实现不同频率腔模之间高保真度的量子态转移.

为了更加全面地理解腔光机械系统的特征，本文研究了2个独立的腔光机械系统中2个腔中光场模纠缠演化的情况，比较初始态参数和时间参数对系统纠缠演化的影响，从而得出系统纠缠在不同参数下的演化趋势.

1 理论模型与计算

实际上，每个腔光机械系统包含2个平行放置的腔镜，其中一个腔镜在系统的一端固定不动，另一个腔镜可在腔中自由移动.当激光驱动共振腔场时，由于光子撞击到可移动镜子上，在可移动镜子表面产生辐射压力，从而使可移动镜子偏离平衡位置引起腔模频率发生变化，通过相互调制使腔镜与腔场耦合起来.本文研究的腔光机械系统模型如图1所示.

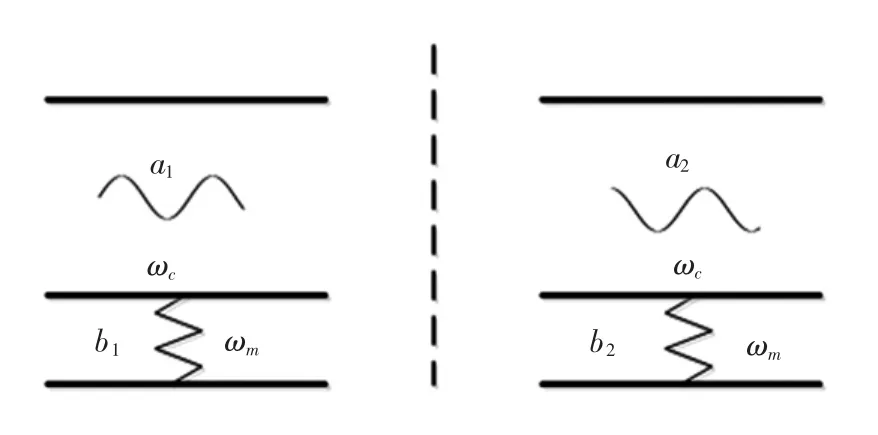
图1 两腔光力学系统的原理图Fig.1 Schematic diagram of two-cavity optomechanical system

假设2个光机械腔完全相同，均处于单模场中并且2个系统之间除了信息交流没有相互作用，系统哈密顿量为：

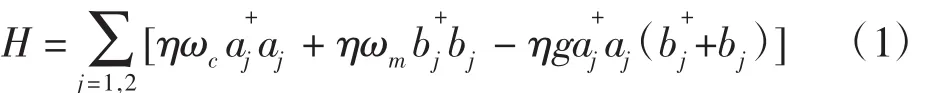
腔场和机械振子的粒子数态分别表示为|m〉a，|n〉b（m，n=0，1，2，…）.在这里只考虑 m，n=0，1这 2种粒子数态.设初始时刻2个腔中的光场模处于纠缠态，系统的初始状态为：

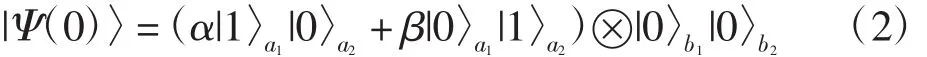
在这里|α|2+|β|2=1.

在相互作用绘景下系统的哈密顿量（1）容易化为：

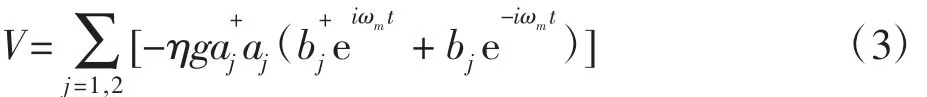
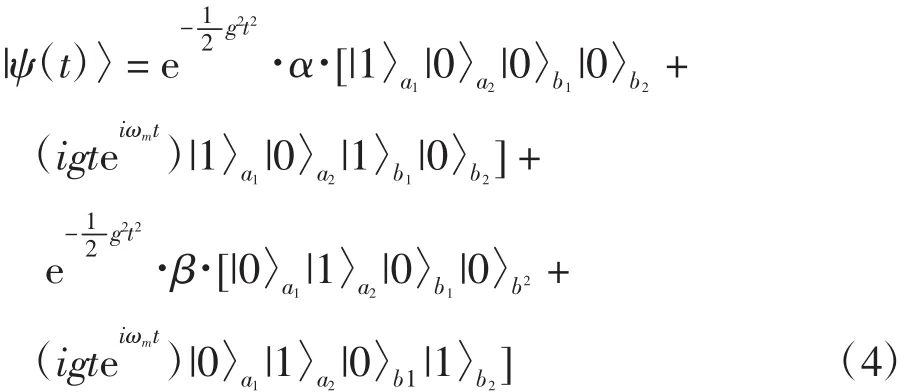
鉴于本文的研究只考虑腔场纠缠态的演化，因此迹去机械振子的作用得到约化密度矩阵ρa1a2（t），归一化后得到一个4×4的矩阵，其矩阵元为：

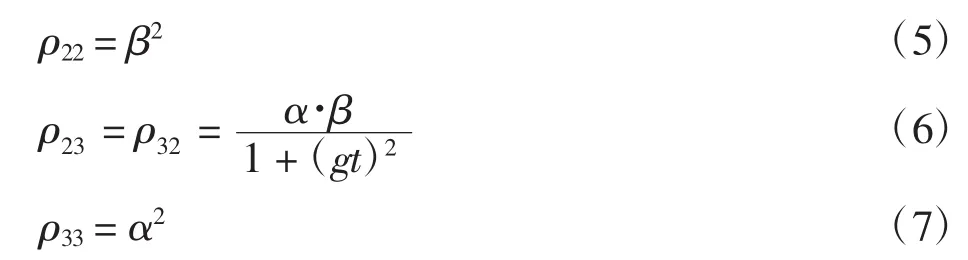
其他矩阵元均为0.根据文献[18]量子纠缠度量的定义式为：

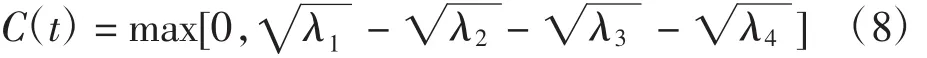
式中：λi为ρ（σy⊗σy）ρ*（σy⊗σy）的本征值；σy为泡利矩阵；ρ为系统的密度矩阵.计算得到所研究系统的量子纠缠度为：

式中.

2 数值分析

图2表示在2个独立腔光机械系统中，2个腔中光场模纠缠C（t）随标度时间和初始态参数α的演化图像.

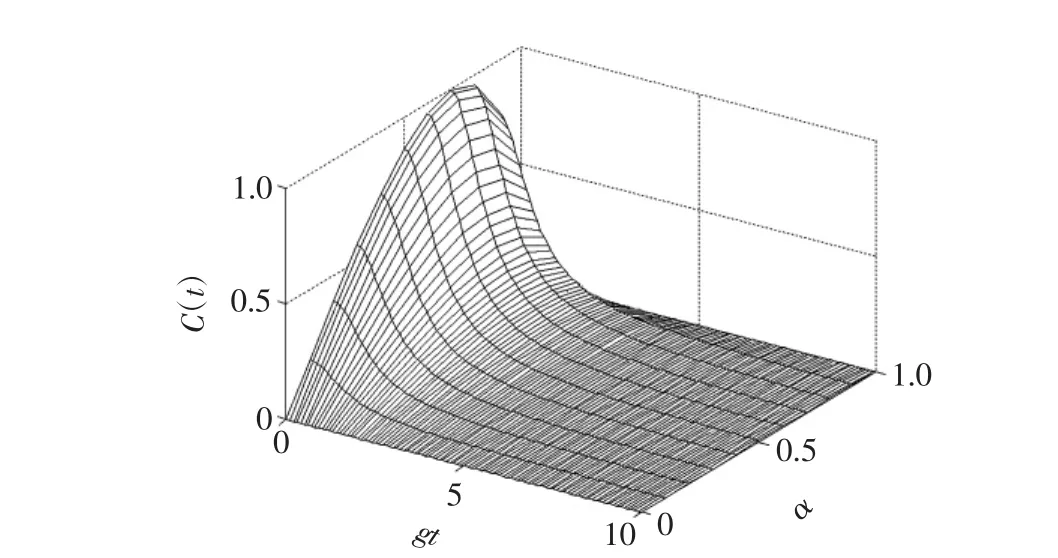
图2 光场模纠缠度C（t）随标度时间gt的演化和参数α的变化Fig.2 Evolution of optical field mode entanglement C（t）with scaled time gt and parameter α

从图2随时间演化走向上看，随着gt的增大，系统的量子纠缠呈衰减的状态，最后衰减为0（即纠缠完全消失）；从图2随初始态参数变化走向上看，随着初始态参数α的增大，系统的量子纠缠先由0开始增大，直到系统的达到最大纠缠度（即C（t）=1）.然后随着参数α的继续增大，系统的纠缠逐渐减小，直到消失为0.

图3表示当初始态参数α取固定值时，系统光场模纠缠度C（t）随gt的演化关系.

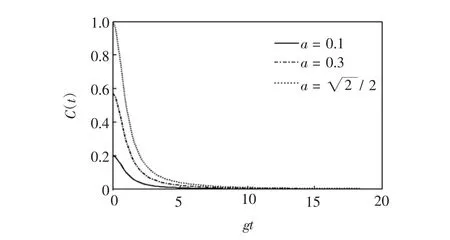
图3 光场模纠缠度C（t）随标度时间gt的演化曲线Fig.3 Evolution of optical field mode entanglement C（t）with scaled time gt

由图3可见，当 α 的取值由逐渐增大时，系统在初始时刻的纠缠度也逐渐增大.当时系统在初始时刻的纠缠度最大（即C（t）=1）.随着初始时刻纠缠度的增大系统纠缠度的衰减速率也增大，但初始时刻纠缠度越大纠缠存在的时间越长，这与图2的演化趋势相吻合.

图4表示当取固定值时，系统光场模纠缠度C（t）随初始态参数α的变化关系.

由图4可以看出，随着gt=1，2，3逐渐增大时，系统的纠缠度C（t）总体变化趋势一样，纠缠度依次减小.系统纠缠度在初始态参数时的逐渐增大的，当时纠缠度最大，在是逐渐减小的，直到减小为0.但是系统纠缠度在前半段的增长速率明显小于在后半段的减小速率.这与图2的演化趋势相吻合.

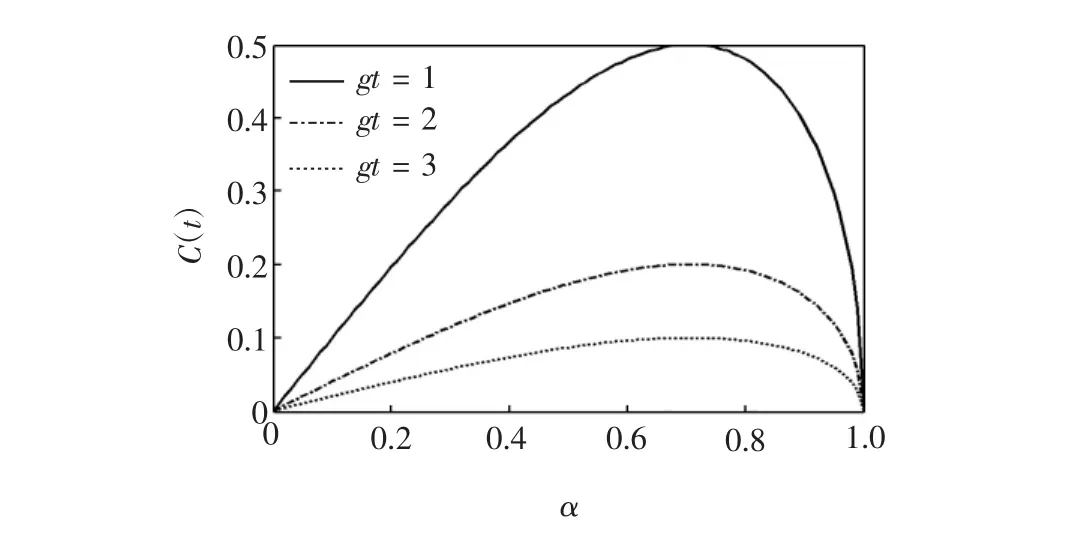
图4 光场模纠缠度C（t）随参数α的变化曲线Fig.4 ChangeofopticalfieldmodeentanglementC（t）with parameterα

这些研究结果对腔光机械系统中纠缠态的制备和如何延长该系统纠缠存在的时间具有一定的借鉴意义.

3 结论

本文研究了双腔光机械系统中2个光场模纠缠演化的动力学行为.分析了标度时间gt与初始态参数α对系统量子纠缠度的影响.通过数值分析得到，系统的量子纠缠随初始态参数α的增大由0逐渐增大到1然后再逐渐减小为0.但是在前半段的增长速率明显小于在后半段的减小速率.初始时刻的系统量子纠缠度越大，纠缠衰减速率就越大.但是初始时刻系统的量子纠缠度越大纠缠存活的时间越长.

[1]ASPELMEYER M，KIPPENBERG T J，MARQUARDT F.Cavity optomechanics[J].Review of Modern Physics，2013，86：1391-1452.

[2]LAHAYE M D，BUU O，CAMAROTA B，et al.Approaching the quantum limit of a nanomechanical resonator[J].Science，2004，304：74-77.

[3]EKINCI K L.Ultimate limits to inertial mass sensing based upon nanoelectromechanical systems[J].Journal of Applied Physics，2003，95：2682-2689.

[4]CAVES C M.Quantum-mechanical radiation-pressure fluctuations in an interferometer[J].Physical Review Letters，1980，45：75-79.

[5]SCHWAB K C，ROUKES M L.Putting mechanics into quan－tum mechanics[J].Physics Today，2005，58：36-42.

[6]COHADON P F，HEIDMANN A，PINARD M.Cooling of a mirror by radiation pressure[J].Physical Review Letters，1999，83：3174-3177.

[7]YAN X Q.Entanglement sudden death of two atoms successive passing a cavity[J].Chaos Solitons&Fractals，2009，41：1645-1650.

[8]YAN X Q，WANG F Z.Quantum discord and entanglement of two atoms in a micromaser-type system[J].Modern Physics Letters B，2016，30（15）：1650190（1）-1650190（16）.

[9]岳转林，闫学群.耗散系统中原子与场熵交换的条件[J].天津工业大学学报，2013，32（6）：81-84.YUE Z L，YAN X Q.Condition for entropy exchange between atom and field in damped system[J].Journal of Tianjin Polytechnic University，2013，32（6）：81-84（in Chinese）.

[10]MANCINI S，GIOVANNETTI V，VITALI D，et al.Entangling macroscopic oscillators exploiting radiation pressure[J].Physical Review Letters，2002，88：120401（1）-120401（4）.

[11]VITALI D，GIGAN S，FERREIRA A，et al.Optomechanical entanglement between a movablemirror and a cavity field[J].Physical Review Letters，2007，98：030405（1）-030405（4）.

[12]BARZANJEH S，VITAIL D，TOMBESI P，et al.Entangling optical and microwave cavity modes by meanes of a nanomechanical resonator[J].Physical Review A，2011，84：042342（1）-042342（4）.

[13]苗长云，罗统荣，白华.基于以太网的多路超声波自动检测系统[J].天津工业大学学报，2016，35（1）：43-49.MIAO C Y，LUO T R，BAI H.Multi-channel automatic ultrasonic testing system based on Ethernet[J].Journal of Tianjin Polytechnic University，2016，35（1）：43-49（in Chinese）.

[14]李鸿强，孙杰，张诚，等.基于AWG的多通道光纤光栅传感解调系统[J].天津工业大学学报，2016，35（2）：65-71.LI H Q，SUN J，ZHANG C，et al.Multi-channel FBG sensor de modulation system based on arrayed waveguide grating（AWG)[J].Journal of Tianjin Polytechnic University，2016，35（2）：65-71（in Chinese）.

[15]RABL P，STANNIGEL K，SORENSEN A，et al.Opto-mechanical transducers for long-distancequantum communication applications[J].Physical Review Letters，2010，105：220501（1）-220501（4）.

[16]STANNIGEL K，KOMAR P，HABRAKEN S J，et al.Optomechanical quantum information processing with photons andphonons[J].PhysicalReviewLetters，2012，109：493-500.

[17]TIAN L.Adiabatic state conversion and pulse transmission in optomechanicalsystems[J].PhysicalReviewLetters，2012，108：329-335.

[18]WOOTTERS W K.Entanglement of formation of an arbitrary state of two qubits[J].Physical Review Letters，1997，80：2245-2248.