基于导引控制一体化设计的水下拦截器迎面拦截最优制导律

杨惠珍, 王 迪, 吕 瑞



基于导引控制一体化设计的水下拦截器迎面拦截最优制导律

杨惠珍1,3, 王 迪1,3, 吕 瑞2,3

(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710077; 3. 水下信息与控制重点实验室, 陕西 西安, 710072)

针对水下拦截器精确制导的系统设计需求, 提出了一种迎面拦截的水下拦截器导引控制一体化最优控制方法。根据水下拦截器与目标的相对运动方程和拦截器动力学方程建立了导引控制一体化数学模型, 采用输出调节器方法设计了导引控制一体化最优控制器, 利用相对运动的视线角和拦截器姿态信息计算出水下拦截器的舵控制指令, 使得视线角收敛至期望值, 从而实现迎面拦截。仿真结果表明, 所提出的迎面拦截制导律迎面拦截效果明显。文中的研究可为水下拦截器的制导系统研制提供理论依据与参考。

水下拦截器; 导引控制一体化; 最优控制; 输出调节器

0 引言

水下拦截器是现代舰艇防御系统中的重要组成部分, 作为主动防御型硬杀伤武器, 已成为当前各国海军研究和发展的重点武器之一。由于拦截目标为来袭鱼雷, 相较于舰艇而言, 具有速度快、体积小、机动性强等特点, 拦截器与来袭目标对抗时间短, 从而要求水下拦截器的导引和控制系统具有精确制导的能力[1]。

传统导引控制系统设计原理见图1。导引系统根据拦截器与目标的相对运动状态生成过载指令, 控制系统根据该指令产生舵偏指令, 从而改变拦截器的姿态和运动轨迹, 使拦截器命中目标。

如图1所示, 传统制导系统设计方法忽略了导引系统和姿态控制系统之间的耦合作用, 将两回路分开进行设计, 要求内环控制系统的时间常数小于外环系统, 否则易出现响应滞后等现象, 造成整个系统失稳, 无法保证命中目标。导引控制一体化(integrated guidance and control, IGC)的主要设计思想则是将导引与控制系统作为一个整体进行设计, 充分考虑拦截器的姿态控制系统对导引系统的影响, 见图2。

一体化控制器综合导引回路与控制回路的作用, 根据目标-拦截器的相对运动和拦截器的姿态信息计算舵偏指令, 在理论上保证整个系统的稳定性, 并且能够提高系统制导精度, 达到精确打击目标的目的[2]。

IGC设计方法在空间拦截器领域有很多相关研究成果, 其设计思路是首先构建拦截器的导引控制一体化模型, 然后采用滑模控制[3-4]、最优控制[5]、自抗扰控制[6]、非线性反演控制[7]等方法设计一体化控制器。然而在水下拦截器研究领域, 关于IGC问题的研究还未见报道。

由于水下目标探测一般采用水声探测方式, 水声自导头安装在拦截器的头部, 其探测范围和探测精度均受到一定的限制。因此, 采用迎面拦截方式有利于拦截器更准确地获得目标信息, 从而提高目标拦截的成功率, 实现有效的防御。迎面拦截可以描述成带终端角约束的制导律设计问题。文献[8]综述了终端角约束的制导律研究成果和未来的应用方向。文献[9]基于滑模变结构控制方法, 考虑了末端满足视线角趋于期望命中姿态角的约束条件, 从而得到零脱靶量和终端角约束的打击效果。文献[10]采用扰动观测器对目标机动进行有效估计, 设计了基于滑模控制的终端角约束导引律, 并利用边界层法对导引律进行改进从而提高系统的鲁棒性。文献[11]采用自适应幂次趋近律结合非奇异终端滑模面, 设计了一种带落角约束的末制导律, 并利用有限时间控制理论给出了求解收敛时间的具体数学表达式。文献[12]运用模糊逻辑处理落角约束变结构控制中出现的抖动问题,针对大机动目标拦截时, 运用BP(ba- ck propagation)神经网络的自适应能力进行了优化设计。文献[13]研究了自适应比例导引律, 通过对导航系数的自适应调整实现对机动目标的有效拦截, 不仅可满足终端角约束, 而且可以实现全向攻击。文献[14]利用拉格朗日法, 构建带有落角约束的导弹运动方程, 基于最优控制方法设计了导引律, 并指出了制导系统中的动力学滞后对脱靶量和落角误差的影响。文献[15]应用Schwarz不等式, 分布研究了控制系统为1阶惯性环节和无惯性环节情况下带落角约束的任意加权最优控制律, 得到制导律的一般表达式, 并可根据不同制导目的, 通过改变加权函数设计相应的制导律。文献[16]针对机动弹头垂直打击目标的要求, 设计了基于最优控制和滑模控制的复合导引律, 并采用径向基函数 (radial basis function, RBF)神经网络自适应调节增益项的方法来减小控制量的抖振和能量损耗。

文中针对水下拦截器精确制导要求, 研究了一种基于导引控制一体化设计的水下拦截器迎面拦截最优制导律[17]。基于水下拦截器与目标的相对运动方程和拦截器水平面侧向运动学与动力学模型, 建立了水下拦截器导引控制一体化数学模型, 采用无限时间输出调节器最优控制方法设计了迎面拦截制导律。仿真结果表明, 所设计的IGC一体化控制器能够使弹道偏角收敛至期望值, 实现了迎面拦截。

1 导引控制一体化数学模型

1.1 水下拦截器与目标的相对运动

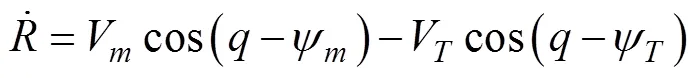
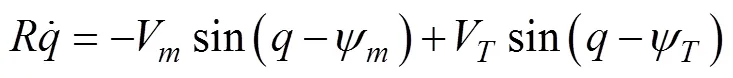
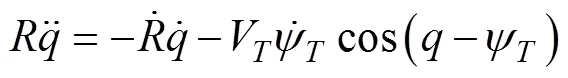
1.2 水下拦截器导引控制一体化数学模型

半速度坐标系下水下拦截器侧向运动方程[18]

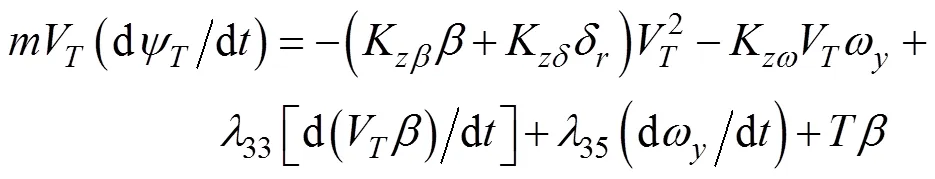
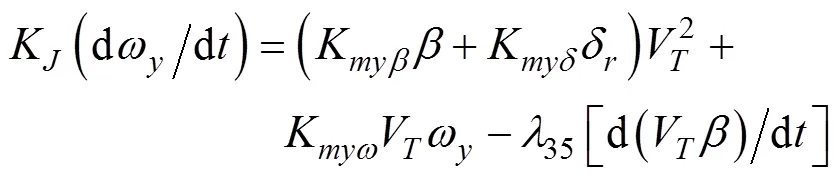
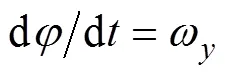
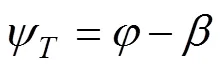
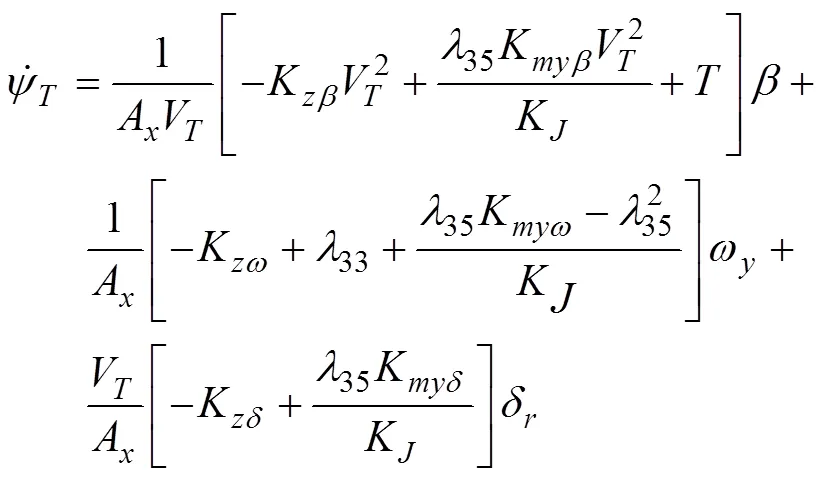
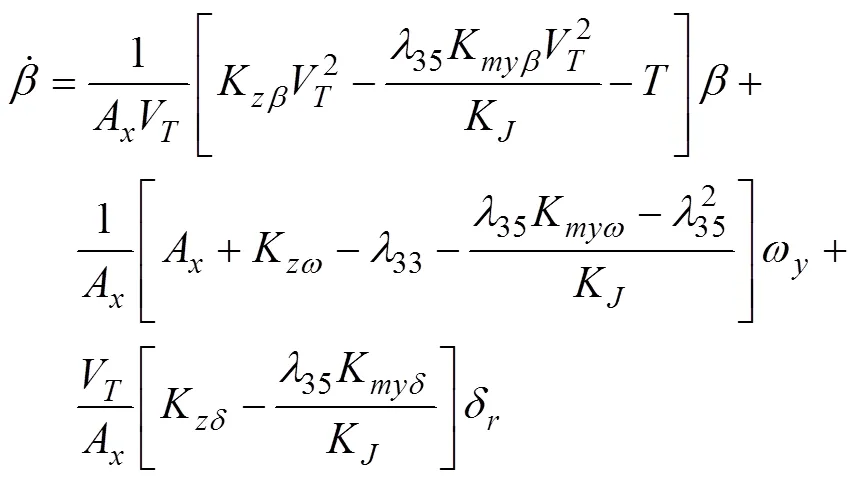
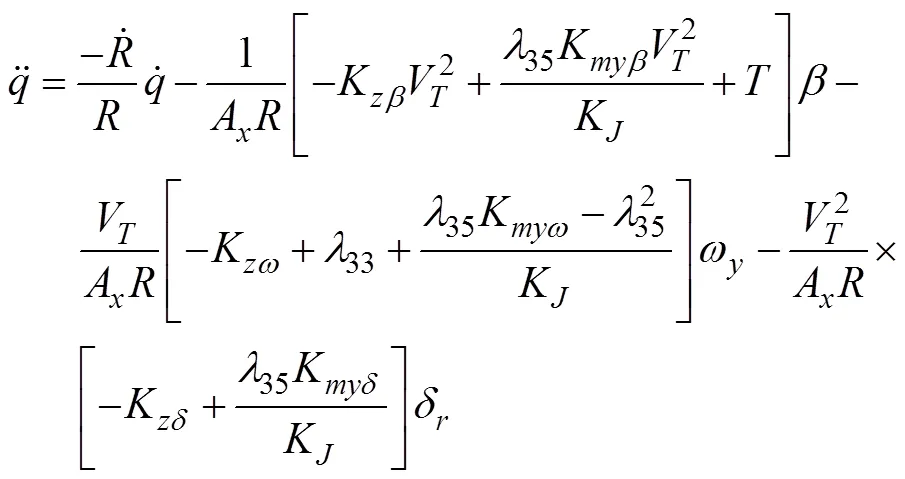
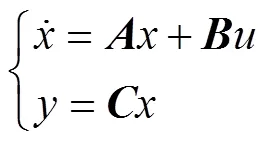
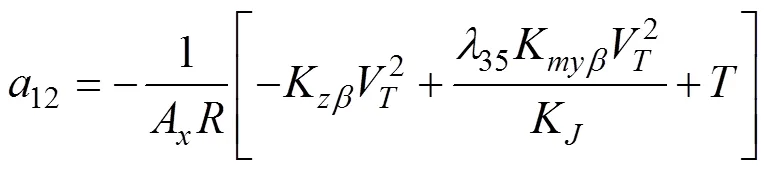
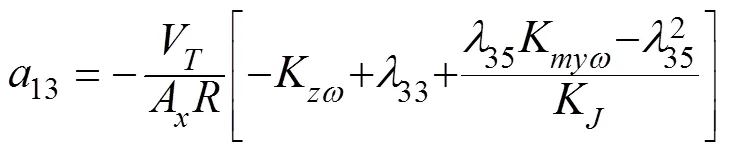
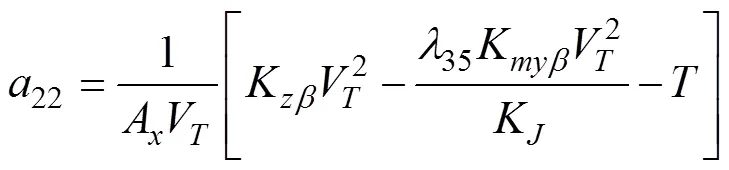
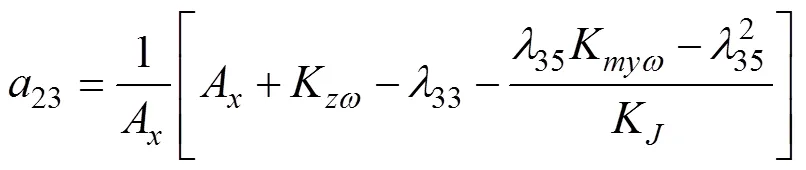
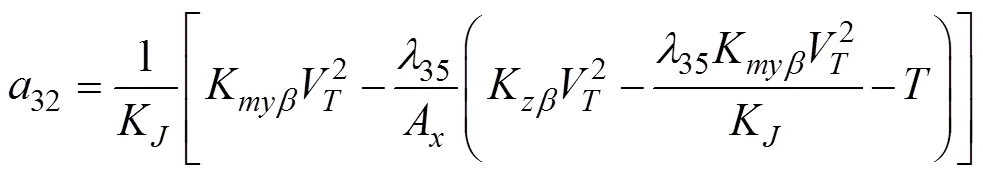
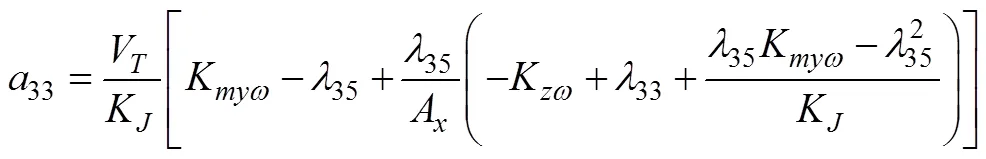
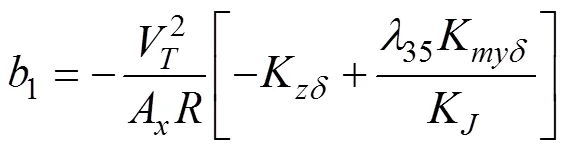
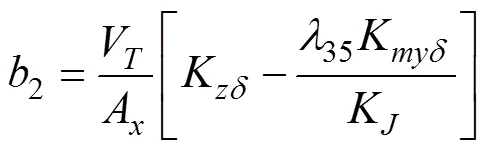
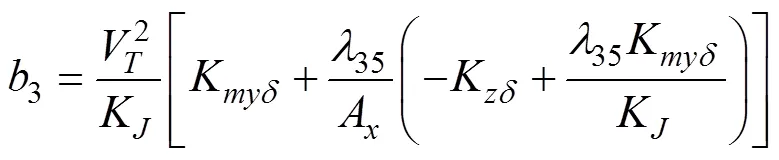
1.3 迎面拦截的水下拦截器IGC模型

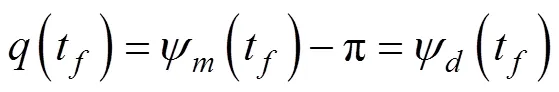
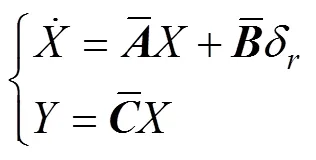
2 基于IGC设计的迎面拦截制导律

对于式(14), 取系统的性能指标

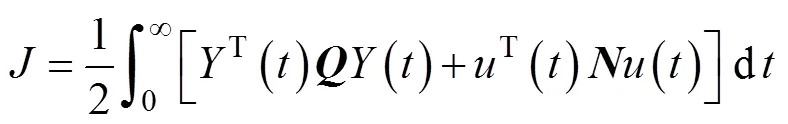
式中:,是正定实对称矩阵。

当系统可控可观时, 存在使性能指标极小的唯一最优控制为

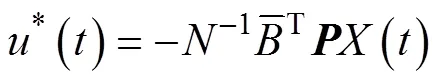
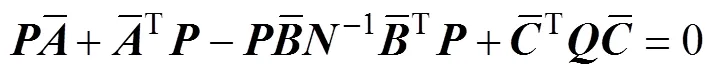
3 仿真结果与分析

图6~图8分别是态势A情况下的拦截轨迹、水下拦截器的姿态变化图及方位角变化轨迹图, 图9~图11则是态势B情况下的仿真结果图。表1列出了2种态势下, 比例导引法和迎面拦截最优制导法在命中时刻的时间、拦截器弹道倾角以及脱靶量。

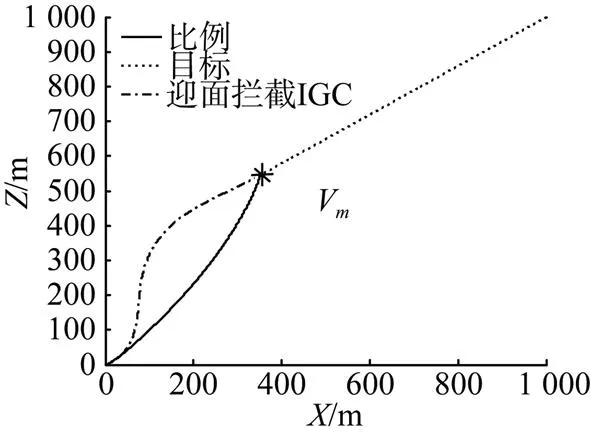
图6 水下拦截器与目标相对运动轨迹图(态势A)

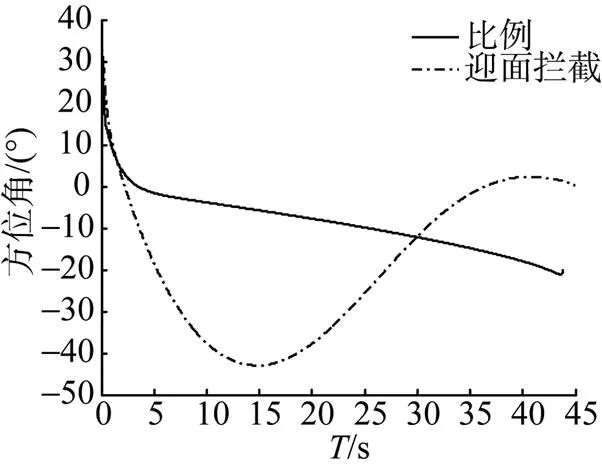
图8 方位角变化范围(态势A)

Fig.8 Variation range of azimuth in situation A

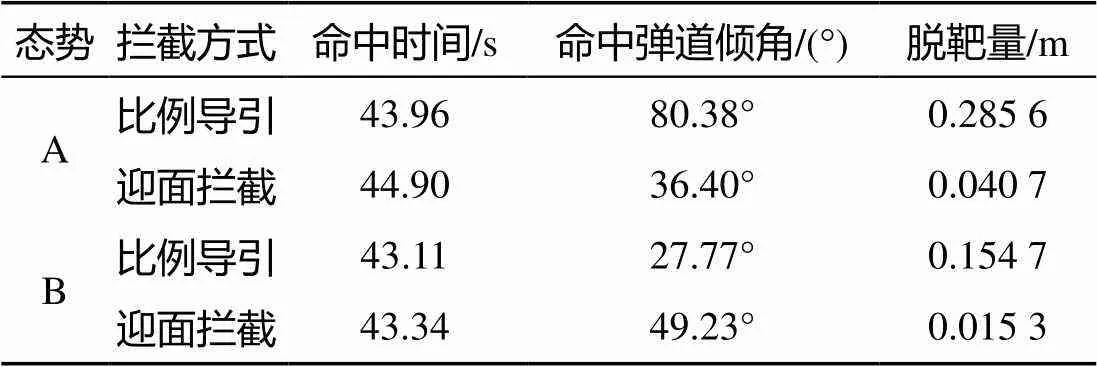
表1 命中参数

4 结束语

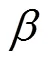
[1] 陈敬军. 国外反舰鱼雷的现状与发展趋势[J]. 声学技术, 2013, 32(2): 164-170.Chen Jing-jun. The Status Quo and Development Trend of Overseas Anti-surface Ship Torpedo[J]. Technical Acoustics, 2013, 32(2): 164-170.

[2] 严晗. 鲁棒非线性导引与控制律一体化设计研究[D]. 合肥: 中国科学技术大学, 2013.

[3] 段广仁, 侯明哲, 谭峰. 基于滑模方法的自适应一体化导引与控制律设计[J]. 兵工学报, 2010, 31(2): 191-198.Duan Guang-ren, Hou Ming-zhe, Tan Feng. Adaptive Int- egrated Guidance and Control Law Design Using Slidin- gmode Approach[J]. Acta Armamentarii, 2010, 31(2): 191-198.

[4] Tal S, Idan M, Oded M, et al. Sliding Mode Control for Integrated Missile Autopilot Guidance[J]. Journal of Gu- idance, Control and Dynamics, 2006, 29(2): 250-260.

[5] Lin C F, Ohlmeyer E, John E. Bibel and Steve Malyevac Optimal Design of Integrated Missile Guidance and Control[C]//1998 AIAA and SAE World Aviation Conference. Anaheim, CA, USA, 1998.

[6] 赵春哲, 黄一. 基于自抗扰控制的制导与运动控制一体化设计[J]. 系统科学与数学, 2010, 30(6): 742-751.

Zhao Chun-zhe, Huang Yi. ADRC Based Integrated Gui- dance and Control Scheme[J]. Journal of System Science and Mathematical Science, 2010, 30(6): 742-751.

[7] 周觐, 雷虎民, 李炯, 等. 导弹俯仰通道制导控制一体化设计[J]. 现代防御技术, 2014, 42(5): 80-84, 90.Zhou Jin, Lei Hu-min, Li Jiong, et al. Design of Integrated Guidance and Control of Missile in Pitch Channel[J]. Mo- dern Defense Technology, 2014, 42(5): 80-84, 90.

[8] 李庆春, 张文生, 韩刚. 终端约束条件下末端制导律研究综述[J]. 控制理论与应用, 2016, 33(1): 1-12.Li Qing-chun, Zhang Wen-sheng, Han Gang. Review of Terminal Guidance Law with Terminal Constraints[J]. Co- ntrol Theory and Applications, 2016, 33(1): 1-12.

[9] 张亚松, 任宏光, 吴震. 等. 带落角约束的滑模变结构制导律研究[J]. 电光与控制, 2012, 19(1): 66-68.Zhang Ya-song, Ren Hong-guang, Wu Zhen, et al. On Sli- ding Mode Variable Stracture Guidance Law with Terminal Angular Constraint[J]. Electronics Optics and Control, 2012, 19(1): 66-68.

[10] 王晓芳, 郑艺裕, 林海. 基于扰动观测器的终端角约束滑模导引律[J]. 系统工程与电子技术, 2014, 36(1): 111- 116.Wang Xiao-fang, Zheng Yi-yu, Lin Hai. Sliding Mode Gu- idance Law with Impact Angle Constraint Based on Dist- urbance Observer[J]. Systems Engineering and Electronics, 2014, 36(1): 111-116.

[11] 张宽桥, 杨锁昌, 王刚. 带落角约束的有限时间收敛末制导律研究[J]. 弹道学报, 2015, 27(4): 30-36.Zhang Kuan-qiao, Yang Suo-chang, Wang Gang. Research of Finite-time Convergence Terminal Guidance Law with Impact Angle Constraint[J]. Journal of Ballistics, 2015, 27(4): 30-36.

(下转第246页)

[12] 刘旭. 带落角约束的模糊神经网络变结构末制导律研究[D]. 沈阳: 沈阳理工大学, 2015.

[13] 张旭, 雷虎民, 曾华, 等. 带落角约束的自适应比例制导律[J]. 固体火箭技术, 2011, 34(6): 687-692.Zhang Xu, Lei Hu-min, Zeng Hua, et al. Adaptive Proportional Navigation with Terminal Angular Constraint[J]. Journal of Solid Rocket Techmology, 2011, 34(6): 687- 692.

[14] 常超, 林德福, 祁载康, 等. 带落点和落角约束的最优末制导律研究[J]. 北京理工大学学报, 2009, 29(3): 233- 236, 239.Chang Chao, Lin De-fu, Qi Zai-kang, et al. Study on the Optimal Terminal Guidance Law with Interception and Impact Angle[J]. Transactions of Beijing Institute of Te- chnology, 2009, 29(3): 233-236, 239.

[15] 张友安, 黄诘, 孙阳平. 带有落角约束的一般加权最优制导律[J]. 航空学报, 2014, 35(3): 848-856.Zhang You-an, Huang Ji, SunYang-pin. Generalized Wei- ghted Optimal Guidance Laws with Impact Angel Constrains[J]. Acta Aeronauticaet Astronautica Sinica, 2014, 35(3): 848-856.

[16] 胡正东, 郭才发, 蔡洪. 带落角约束的再入机动弹头的复合导引律[J]. 国防科技大学学报, 2008, 30(3): 21-26.Hu Zheng-dong, Guo Cai-fa, Cai Hong. Integrated Guidance Law of Reentry Maneuvering Warhead with Termianl Angular Constraint[J]. Journal of National University of Defense Technology, 2008, 30(3): 21-26.

[17] 杨惠珍. 基于扩张状态观测器的反鱼雷鱼雷迎面拦截制导律[J]. 鱼雷技术, 2014, 22(3): 179-183. Yang Hui-zhen. Extended State Observer-Based Head-on Intercept Guidance Law for Anti-Torpedo Torpedo[J]. To- rpedo Technology, 2014, 22(3): 179-183.

[18] 徐德民. 鱼雷自动控制系统[M]. 西安: 西北工业大学出版社, 2001.

(责任编辑: 杨力军)

An Optimal Head-on Guidance Law for Integrated Guidance and Control of Underwater Interceptor

YANG Hui-zhen1,3, WANG Di1,3, LÜRui2,3

(1. College of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China; 2. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China; 3.Science and Technology on Underwater Information and Control Laboratory, Xi’an 710072, China)

This paper proposes an optimal head-on control approach for integrated guidance and control of an underwater interceptor by considering the design requirements of precise guidance system for the underwater interceptor. An integrated guidance and control model is established based on the kinetic equation of relative motion and hydrodynamic equation of the underwater interceptor. Using the output regulator method, an optimal controller for the integrated guidance and control system is developed. This controller calculates the rudder control command with the data of sight line angle and interceptor’s attitudes to achieve the purpose of head-on intercepting target by making the sight line angle converge to the desired value. Simulation results show the effectiveness of the proposed head-on guidance law. This research may provide a theoretical basis and a reference for development of guidance system for the underwater interceptor.

underwater interceptor; integrated guidance and control; optimal control; output regulator

杨惠珍, 王迪, 吕瑞. 基于导引控制一体化设计的水下拦截器迎面拦截最优制导律[J]. 水下无人系统学报, 2018, 26(3): 228-233.

TJ63; TJ765

A

2096-3920(2018)03-0228-06

10.11993/j.issn.2096-3920.2018.03.007

2018-03-09;

2018-06-08.

杨惠珍(1974-), 女, 副教授, 博士, 主要研究方向为自主水下航行器制导与控制技术.