基于静力试验的鱼雷壳体模态计算模型修正

王 升, 尹韶平, 郭 君, 王 中, 张志民



基于静力试验的鱼雷壳体模态计算模型修正

王 升1,2, 尹韶平1, 郭 君1, 王 中1,2, 张志民1

(1. 中国船舶重工集团公司 第705研究所, 陕西 西安 , 710077; 2. 水下信息与控制重点实验室, 陕西 西安, 710077)

为建立一种简单而又适用的鱼雷壳体楔环连接结构模态计算分析模型, 将楔环连接的鱼雷壳体简化为2个壳体以及1个环形圈连接的有限元模型, 其中包含7对接触面以及1个接触刚度参数。通过鱼雷壳体的静力加载试验以及静力仿真对比, 辨识出模型中的接触刚度参数。对修正后的有限元模型进行模态仿真计算, 仿真模态频率与试验模态频率误差不大于2.65%, 结果表明了该模态计算方法的准确性。可为鱼雷壳体等含楔环连接结构的有限元建模与模态分析提供借鉴。

鱼雷壳体; 楔环连接结构; 模态仿真; 模型修正

0 引言

鱼雷壳体声辐射对鱼雷的综合作战效能影响重大, 对鱼雷的攻击隐蔽性、线导导引有效性、自导性能及发射平台的安全性均有重要影响[1]。鱼雷壳体的声辐射研究中最主要的一环是全雷模态计算, 在鱼雷复杂的力学环境影响下, 全雷模态计算不准确会导致不可意料的共振现象发生, 共振往往会引起较大振动能级的全雷振动噪声, 甚至造成结构破坏或者设备元件的损坏[2]。

在对鱼雷做模态仿真计算时, 受楔环连接结构复杂的静动力学特性影响, 不能准确地建立有限元分析模型, 会使得仿真计算结果误差较大, 这种误差会造成很多不可避免的损失与危险。如何方便、准确地对鱼雷壳体连接结构进行简化处理, 如何正确地设置有限元模型的参数, 将直接影响到鱼雷模态仿真的准确性。

国内学者针对不同的研究内容, 采取的楔环连接结构模型的简化方式以及楔环连接结构的仿真计算方法大不相同。黄鹏等[3]在楔环连接结构2种有限元优化设计方案研究中, 建立楔环连接结构的参数化有限元模型, 以结构最大应力比为目标函数, 对楔环径向和轴向尺寸进行优化仿真设计。王路等[4]在workbench响应谱分析的鱼雷振动传递优化中, 基于结构参数化等效模型, 进行优化计算, 降低结构振动传递响应。马锐磊等[5]在鱼雷楔环连接结构等效刚度建模与模态分析中, 采用了等效弹性模量法对鱼雷楔环连接结构进行仿真计算。严海等[6]在模态参数的水下航行器楔环结构有限元模型修正中, 基于固有频率和模态振型等模态参数修正有限元模型。赵荣国[7]在楔环连接结构静力接触行为与动力学特性研究中, 将楔环连接结构简化处理后, 调整接触面积以及接触罚刚度系数修正有限元模型。

文中通过楔环连接壳体的静力加载试验以及静力仿真, 对楔环连接结构有限元模型进行修正, 采用修正后的有限元模型进行鱼雷壳体的模态仿真计算, 并与修正前模型计算结果进行比较, 结果表明了该计算方法的准确性。

1 模态理论

多自由度一般粘性阻尼结构系统动力学微分方程[8]为

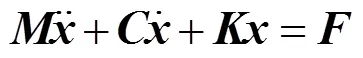
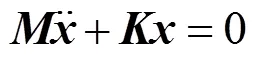
设式(2)的特解为

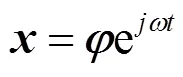
将式(3)代入式(2), 得

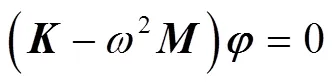
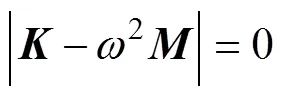
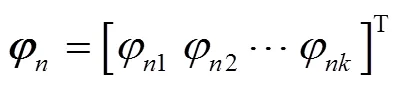
2 鱼雷壳体建模

2.1 楔环连接结构模型简化

取研究对象为楔环连接的2段鱼雷壳体, 材料为铝合金。其中, 楔环连接部分由上壳体、2个楔环带、下壳体、密封圈、填片和盖板等组成。楔环结构的接触面对较多, 有诸多肋骨、槽、孔、倒角和圆角等特征, 不便于有限元网格的划分, 且计算耗时, 容易造成仿真计算不收敛。因此, 有必要对楔环结构的有限元模型进行简化处理, 简化了如小孔、槽、倒角及圆角等一些不影响整体结构响应的特征。由于2个楔环带满足自锁条件, 可视为一个整体, 且不关心2个楔环带之间的受力状况, 所以将2个楔环带看做1个环形圈, 方便建模, 简化后的模型物理参数如表1所示。

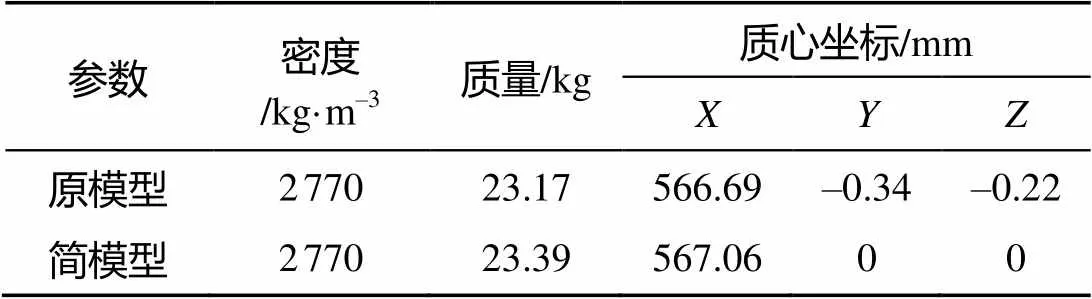
表1 模型物理参数

由表1可以看出, 简化后的模型与实际结构主要参数相差不大, 简化模型可用于仿真分析, 确保仿真结果具有较高的可信度。

2.2 基于Hypermesh的有限元模型网格划分

采用UG建立鱼雷壳体几何模型后, 在Hypermesh中进行网格划分[9], 大部分采用hex六面体单元, 局部采用penta6五面体单元。共计48 860个单元, 其中楔环有6 000个网格, 舱段壳体1有30 480个网格, 舱段壳体2有12 380个网格, 网格质量检查良好。有限元模型如图1所示, 局部接触部分网格如图2所示。

2.3 有限元模型设置

将网格模型导入Workbench中, 建立有限元仿真模型[10]。

接触面和目标面的选择一般有如下原则:

1) 根据接触面材料属性选择, 材料较软的应当选为目标面, 材料硬的选为接触面;

2) 接触面的网格一般比目标面网格细密;

3) 划分了低阶单元的表面应为目标面;

4) 表面较大的应为目标面;

5) 应该选取平面或凹面为目标面。

依据以上原则, 共设置了7对接触面, 如图2所示, 分别为楔环与鱼雷舱段壳体1之间的2对接触面, 即为图中编号①、②部分, 其中楔环为接触体, 舱段壳体1为目标体; 楔环与鱼雷舱段壳体2之间的2对接触面, 即图中编号③、④部分, 其中楔环为接触体, 舱段壳体2为目标体; 鱼雷舱段壳体1与鱼雷舱段壳体2之间的3对接触面, 即图中编号⑤、⑥、⑦部分, 其中舱段壳体1为接触体, 舱段壳体2为目标体。接触面与目标面采用绑定方式, 非对称接触行为, 采用pure penalty接触算法, 通过高斯点(Gauss point)探测接触状态, 罚刚度系数为待修正参数, 其余保留默认设置, 至此完成鱼雷连接壳体有限元仿真模型的建立。

3 鱼雷舱段壳体静力加载试验

3.1 静力加载试验

通过静力加载试验, 测试楔环连接结构在外载下测点的位移量, 用于修正有限元仿真模型。

如图3所示, 本次试验试件为楔环连接的2段鱼雷舱段壳体, 试验工装有壳体紧固工装、转接工装、位移补偿工装以及加载工装, 其中位移补偿工装固定在紧固工装上, 用于补偿试验中工装位移变形而引起的试件位移变形量。试验机为电子万能试验机。

试件上的测点布局如图4所示, 测点A、B、C位于试件侧面, 距离右端面距离依次为100 mm, 200 mm, 400 mm。

载荷加载方式为1 mm/min的等速位移加载, 每个载荷步保载30 s, 记录每个载荷下所有测点的位移。载荷步如下: 600 N→1200 N→1800 N→2400 N→3000 N→3600 N→4200 N→4800 N→5400 N→6000 N→6600N→7200 N→7800 N→8400 N。

3.2 静力加载试验结果

将万能实验机的端力值和位移值清零, 百分表调零后开始试验, 试验现场如图5所示。

测点A、B和C的位移测量值如表2所示。

表2 测点位移值

4 鱼雷舱段壳体有限元模型修正

4.1 静力试验仿真

采用Hypermesh建立包含工装夹具的鱼雷舱段壳体有限元模型, 其中鱼雷舱段壳体模型的网格划分与2.2节相同, 壳体模型与紧固工装、加载工装共划分有65 687个单元。将模型导入workbench中进行仿真计算, 鱼雷壳体的有限元模型设置同2.3节, 壳体与紧固工装、壳体与加载工装的接触部分均采用绑定方式, 并保留默认设置。楔环连接的2段壳体以及紧固工装材料为铝合金材料, 加载工装材料为结构钢, 静力仿真有限元模型如图6所示。

约束紧固工装下端面的全部自由度, 在加载工装上施加8400 N的力载荷, 方向竖直向下。计算结构的整体变形。整体变形如图7所示, 图中(a)图为前视图; (b)图为俯视图; (c)图为右视图。由图可知, 试件的右端发生椭圆形形变, 造成试件的底端发生局部向上弯曲。

4.2 试验结果与分析

采用测点A、B、C的数据修正楔环接触结构接触面的罚刚度系数, 进行仿真计算。经过多次试算, 取罚刚度系数=0.000 08时, 测点A、B、C的仿真结果与试验结果的比较如表3所示, 与试验数据拟合较好, 拟合曲线如图8所示。

图8可知, 当载荷力大于3600 N(认为此时鱼雷壳体连接结构接触状态趋于稳定)时, 误差均小于20%, 测点A、B、C的仿真数据与试验数据拟合得很好, 即罚刚度系数=0.000 08时的面接触刚度与楔环连接刚度接近, 可用于有限元模型的模态仿真计算。

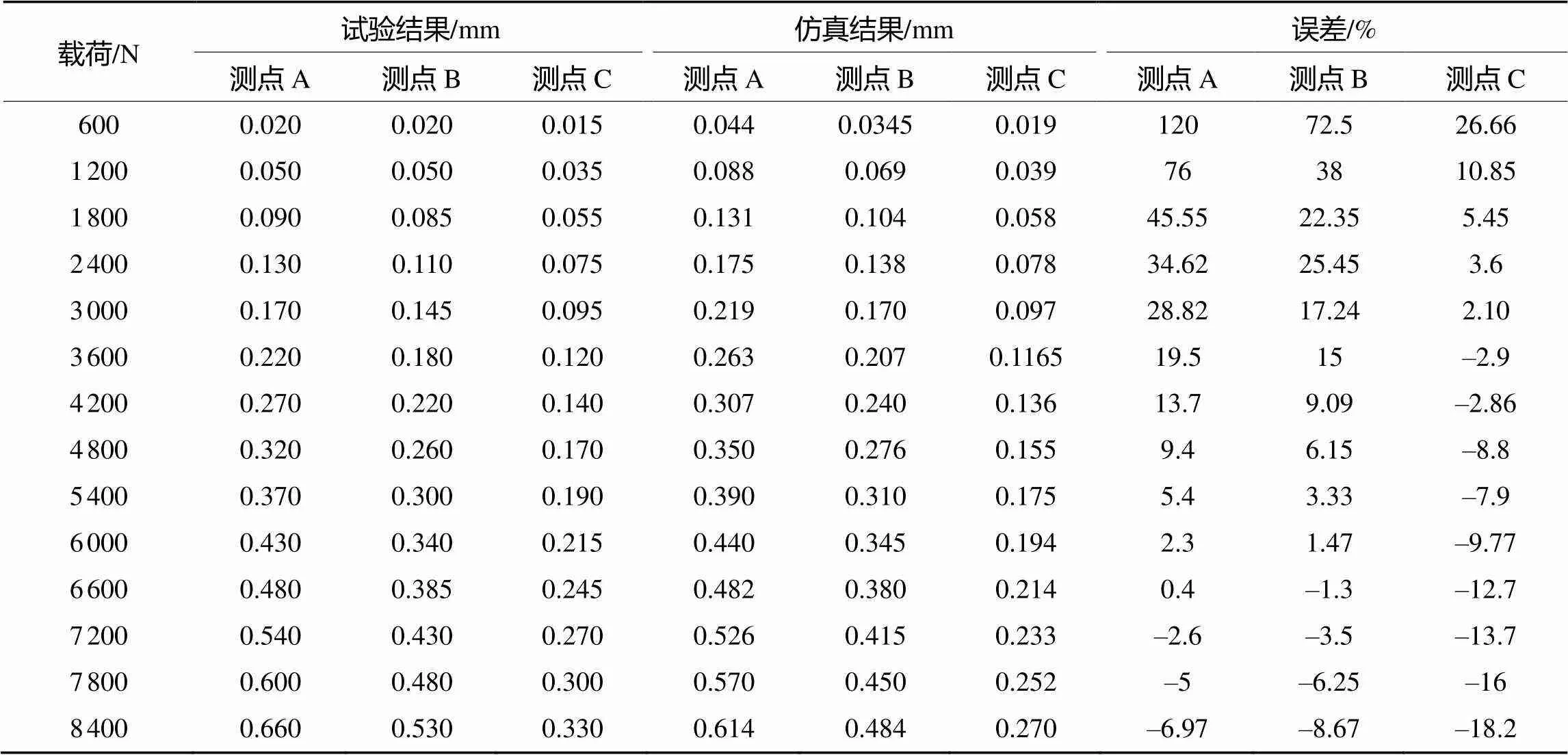
表3 仿真结果与试验结果比较

5 鱼雷舱段壳体模态计算

初步仿真计算时, 罚刚度系数值采用默认设置, 即=1。计算分析得前6阶模态频率, 与试验模态频率的比较如表4所示。

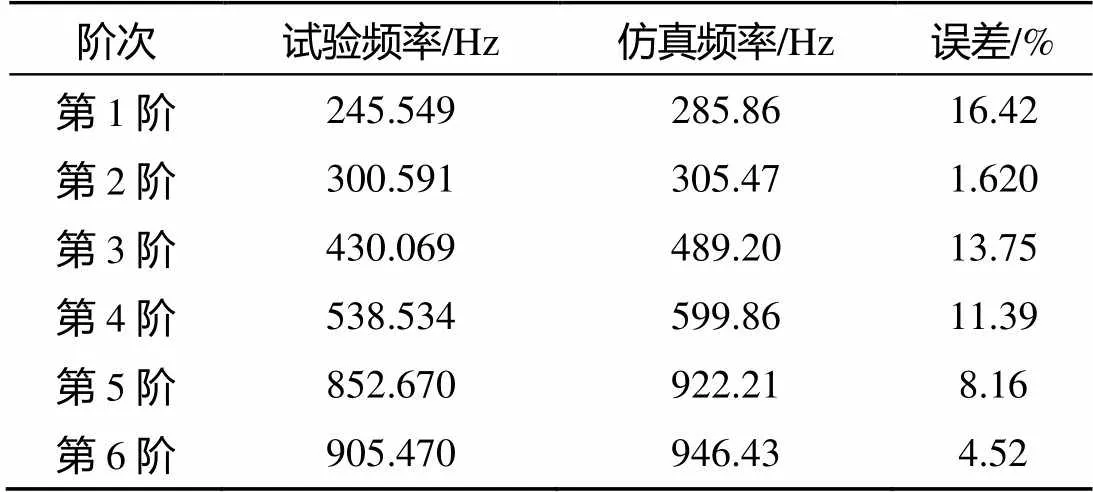
表4 模型修正前仿真计算结果

由表4可知, 仿真结果与试验结果误差较大, 须对有限元模型进行修正, 采用静力仿真得到的罚刚度系数FKN=0.000 08再次进行模态计算, 得到的结果与试验模态频率的比较如表5所示, 仿真模态振型如图9所示。由表5可知, 仿真结果与试验结果的误差均不大于2.65%, 远好于修正前模型计算结果。由图9可知, 仿真振型与试验振型一致, 表明基于静力试验修正后的有限元模型能够更准确地对鱼雷壳体进行模态仿真计算。

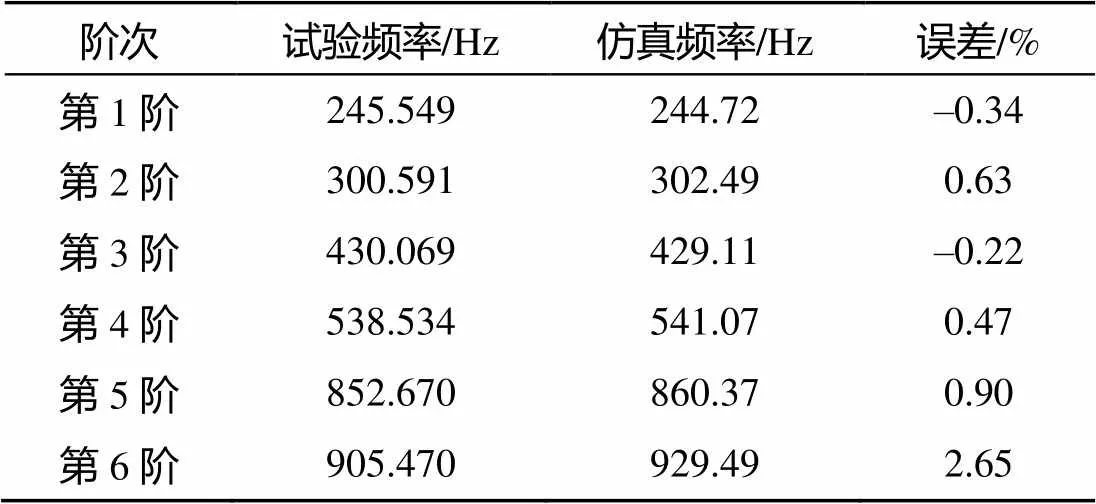
表5 模型修正后仿真计算结果

6 结束语

文中建立了一种只有7对接触面的鱼雷舱段壳体有限元模型, 基于鱼雷壳体静力加载试验结果, 修正楔环连接的有限元模型, 并用于模态仿真计算。修正后模态频率结果与试验模态频率误差不大于2.65%, 准确度较高。为鱼雷的模态仿真计算提供了一种方便、适用、准确的模型简化方式以及有限元模型修正方法。

[1] 尹韶平, 刘瑞生. 鱼雷总体技术[M]. 北京: 国防工业出版社, 2011.

[2] 尹韶平. 鱼雷减振降噪技术[M]. 北京: 国防工业出版社, 2016.

[3] 黄鹏, 尹益辉, 莫军. 楔环连接结构两种有限元优化设计方案研究[J]. 机械工程学报, 2006, 42(8): 205-209.Huang Peng, Yin Yi-hui, Mo Jun. Two Optimization Designs Research of Wedge-Ring Joint Structure Based on FEM[J]. Chinese Journal of Mechanical Engineering, 2006, 42(8): 205-209.

[4] 王路, 尹韶平, 曹小娟, 等. 基于Workbench响应普分析的鱼雷振动传递优化[J]. 鱼雷技术, 2016, 24(1): 13-17.Wang Lu, Yin Shao-ping, Cao Xiao-juan, et al. Vibration Transfer Optimization of Torpedo Based on Workbench Response Spectrum[J]. Torpedo Technology, 2016, 24(1): 13-17.

[5] 马锐磊, 尹韶平, 曹小娟, 等. 鱼雷楔环连接结构等效刚度建模与模态分析[J]. 舰船科学技术, 2014, 36(2): 143-147.Ma Rui-lei, Yin Shao-ping, Cao Xiao-juan, et al. Research on Finite Element Modeling and Modal Analysis of Torpedo’s Wedged-Ring Connection Structure[J]. Ship Science and Technology, 2014, 36(2): 143-147.

[6] 严海, 马锐磊, 梁跃, 等. 基于模态参数的水下航行器楔环结构有限元模型修正[J]. 鱼雷技术, 2016, 24(2): 87-93.Yan Hai, Ma Rui-lei, Liang Yue, et al. Finite Element Model Correction for Wedged-Ring Connection Structure of Underwater Vehicle Based on Modal Parameters[J]. Torpedo Technology. 2016, 24(2): 87-93.

[7] 赵荣国. 楔环连接结构静力接触行为与动力学特性研究[D]. 绵阳: 中国工程物理研究院, 2004.

[8] 曹树谦, 张文德, 萧龙翔. 振动结构模态分析[M]. 天津: 天津出版社, 2014.

[9] 彭妍, 娄一青, 汪亚超, 等. 基于HyperMesh软件的复杂结构有限元建模[J]. 水电能源科学, 2010, 28(8): 100-105.Peng Yan, Lou Yi-qing, Wang Ya-chao, et al. Finite Element Model of Complex Structure Based on Hypermesh Software[J]. Water Resources and Power. 2010, 28(8): 100-105.

[10] Gu R J, Murty P, Zheng Q. Use of Penalty Variable in Finite Element Analysis of Contacting Objects[J]. Compu- ters & Structures, 2002, 80(31): 2449-2459.

(责任编辑: 陈 曦)

Correction of Modal Calculation Model for Torpedo Shell Based on Static Test

WANG Sheng1,2, YIN Shao-ping1, GUO Jun1, WANG Zhong1,2, ZHANG Zhi-min1

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi’an 710077, China)

The torpedo shell joined with wedge-ring connection is simplified as two shells and one annular ring. This simple structure is modeled to build a simple, applicative finite element analysis model, which contains seven contact surfaces and a parameter of contact stiffness coefficient. Static loading test and static simulation analysis are conducted to identify the contact stiffness of the model. The modal of the modified model is calculated via simulation, and the relative error of the modal frequency between simulation and modal test is not more than 2.65%, verifying the accuracy of the proposed modal simulation method. This study may provide a reference for finite element modeling and modal simulation of the structures with wedge-ring connection, such as torpedo shell.

torpedo shell; structure with wedge-ring connection; modal simulation; model correction

王升,尹韶平,郭君,等. 基于静力试验的鱼雷壳体模态计算模型修正[J].水下无人系统学报, 2018, 26(3): 247-252.

TJ630.3; TP391.9

A

2096-3920(2018)03-0247-07

10.11993/j.issn.2096-3920.2018.03.010

2017-08-29;

2017-11-02.

王 升(1992-), 男, 在读硕士, 主要研究方向为鱼雷总体技术.