参数摄动下基于积分滑模的欠驱动UUV轨迹跟踪控制方法

严浙平, 李 响, 宋育武, 李 娟, 3



参数摄动下基于积分滑模的欠驱动UUV轨迹跟踪控制方法

严浙平1, 李 响1, 宋育武2, 李 娟1, 3

(1. 哈尔滨工程大学 自动化学院, 黑龙江 哈尔滨, 150001; 2. 空军哈尔滨飞行学院 理论训练系, 黑龙江 哈尔滨, 150001; 3. 哈尔滨工程大学 水下机器人技术重点实验室, 黑龙江 哈尔滨, 150001)

针对参数摄动下欠驱动无人水下航行器(UUV)水平面轨迹跟踪控制问题, 提出了一种基于积分滑模的轨迹跟踪控制方法。该方法利用航行器的运动特性建立轨迹跟踪误差方程, 结合反步法和积分滑模控制方法, 分别设计了1阶积分滑模纵向速度控制器和偏航角速度控制器, 实现了参数摄动下水平面轨迹跟踪并证明了系统的稳定性。仿真结果表明, 所提出的轨迹跟踪控制方法可以有效地完成轨迹跟踪任务并且对参数摄动具有很强的鲁棒性。

欠驱动UUV; 轨迹跟踪; 参数摄动; 积分滑模控制; 反步法

0 引言

近年来, 随着海洋开发的日益深入, 无人水下航行器(unmanned undersea vehicle, UUV)在海洋科学调查、海洋资源勘探以及海底地形勘察等方面得到了广泛应用, 而UUV轨迹跟踪控制是实现上述任务的技术基础[1-2]。综合考虑UUV的总体质量、推进效率等方面, UUV的运动执行机构通常设计为欠驱动模式, 文中研究的UUV在水平方向缺少直接的推进器, 属于典型的欠驱动系统。此外, 欠驱动UUV运动系统还会受到参数摄动、海流等内外扰动的影响[3], 增加了欠驱动UUV运动控制器的设计难度。

目前, 国内外学者对欠驱动UUV轨迹跟踪控制的研究已经取得了一定成果。比较常见的控制方法有反步控制[4-6]、滑模控制[7-10]、自适应控制[11-12]及神经网络控制[13-14]等。Repoulias等[5]基于反步控制和Lyapunov稳定性理论设计欠驱动轨迹跟踪控制器, 实现了欠驱动UUV水平面轨迹跟踪控制。但该方法需要确定UUV模型参数, 同时要求UUV偏航速度非零, 即不能跟踪直线。Yu等[8]基于滑模理论设计轨迹跟踪控制器, 针对文献[5]和[6]做出了一定的改进。但是, 该方法将UUV 3个自由度的阻力模型近似为线性函数, 使控制器只适用于UUV低速运动。贾鹤鸣等[14]引入神经网络模型, 实现了UUV的轨迹跟踪控制, 但训练神经网络需要选取合适的样本, 而且神经网络的自适应学习需要一定时间, 会影响UUV的实时性。Zhou等[15]在反步法基础上, 引入生物启发算法对速度做自适应调节, 避免了反步法微分爆炸和拐点跳变问题, 但该控制器仅对直线轨迹仿真验证, 未对曲线轨迹进行分析验证。严浙平等[16]基于终端滑模理论提出双闭环控制策略, 实现了UUV空间螺旋线轨迹跟踪, 并证明了该方法在有限时间内收敛, 但该策略针对全驱动UUV有效。上述轨迹跟踪问题的研究中, 大多假设航行器的运动模型为精确模型。而在UUV实际运动中其水动力系数的精确值很难获得; 此外, 当航行器航行于近水面或近海底面时, 由于流场边界条件的改变, 也会导致 UUV 的水动力系数产生摄动[17]。因此, 设计欠驱动UUV的运动控制器需要考虑对于参数摄动的鲁棒性。

针对欠驱动 UUV 的水动力参数摄动问题, 文中设计一种基于积分滑模控制的轨迹跟踪控制器。首先在期望轨迹上引入虚拟航行器, 建立轨迹跟踪误差方程。然后, 利用积分滑模控制方法分别设计运动学控制器和动力学控制器, 从而实现欠驱动UUV的平面轨迹跟踪控制。最后, 证明所提出的跟踪控制方法能够有效镇定跟踪误差。

1 UUV误差模型

由于文中对欠驱动UUV的水平面运动控制展开研究, 因此航行器的动力学建模可以忽略深沉运动、纵倾运动和横倾运动的影响, 欠驱动UUV运动学方程[18]

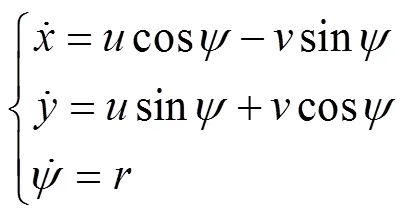
欠驱动UUV的水平面动力学方程

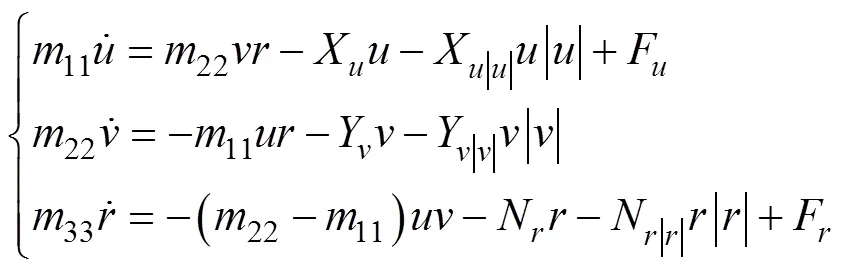
对于UUV的轨迹跟踪控制问题, 一般是通过引入适当的航行器运动状态误差空间, 将轨迹跟踪控制问题转化为镇定问题。欠驱动UUV平面轨迹跟踪示意图如图1所示。

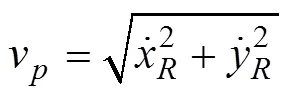
UUV的航迹角

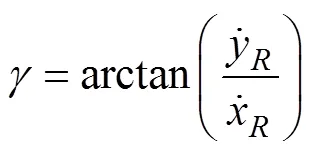
UUV的漂角

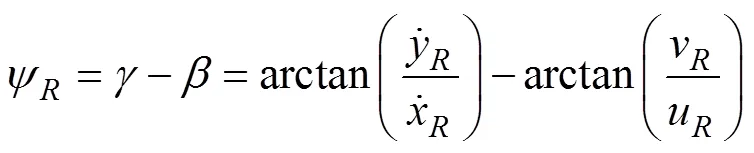
UUV在船体坐标系下的期望横向速度

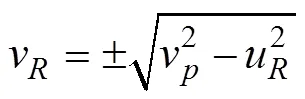
定义轨迹跟踪误差变量

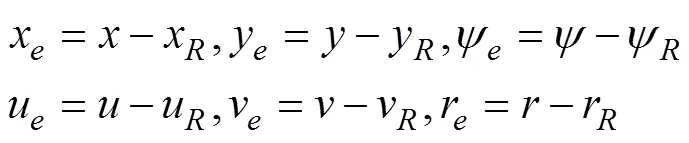
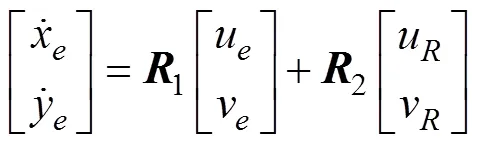
其中

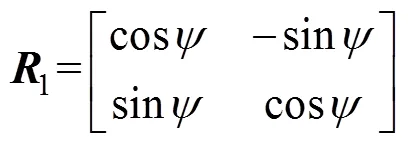
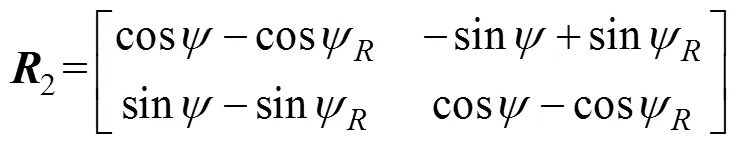
将式(9)带入式(2)中, 得到动力学误差方程

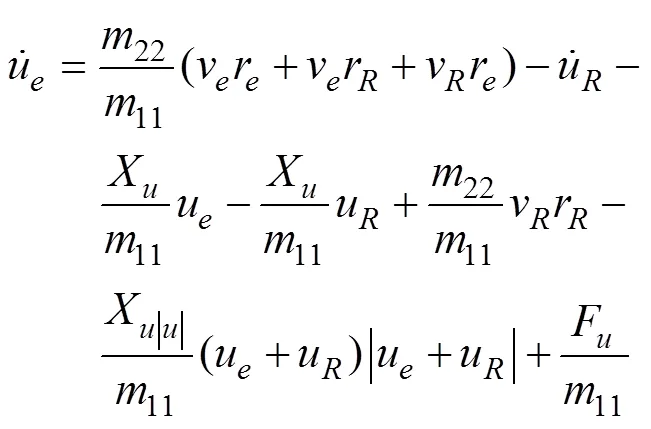
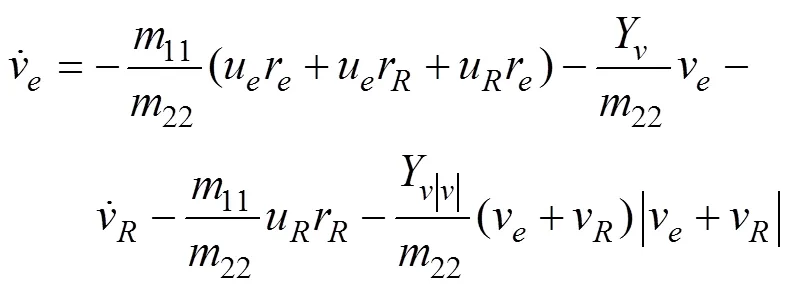
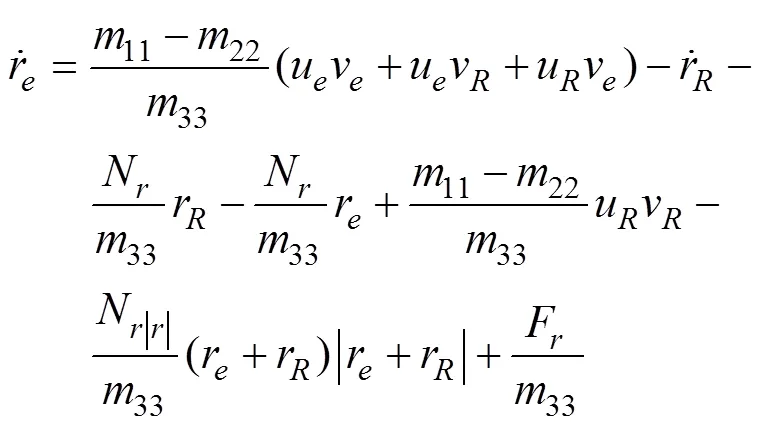
2 UUV轨迹跟踪控制器设计

2.1 运动学跟踪控制器

引入如下1阶积分滑模面

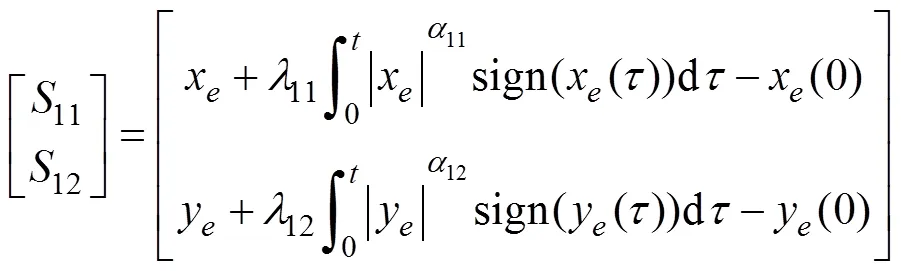
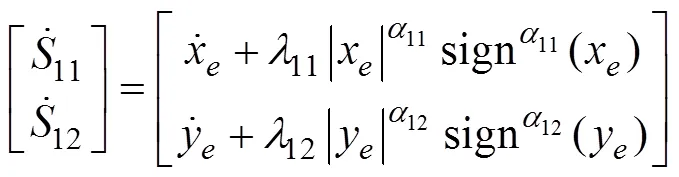
令式(18)等于0, 带入式(10), 可得到跟踪误差子系统的期望控制输入

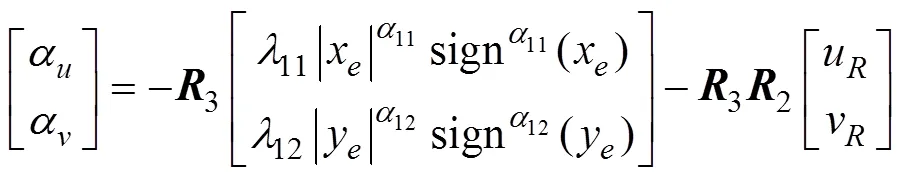
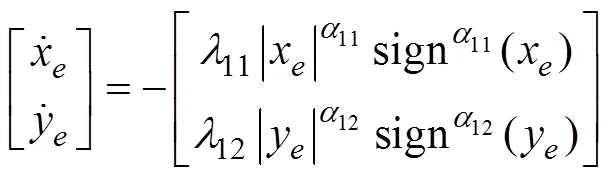
2.2 动力学跟踪控制器

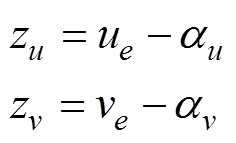
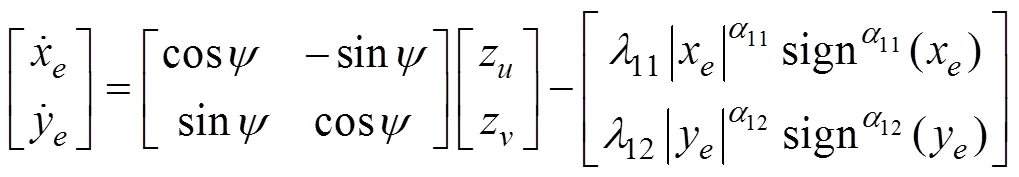
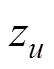
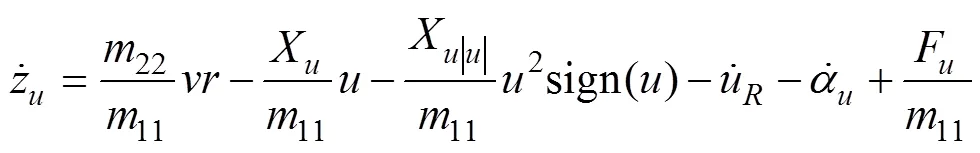
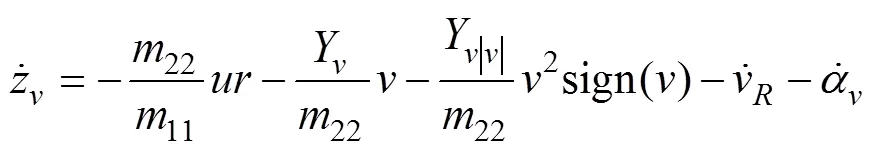
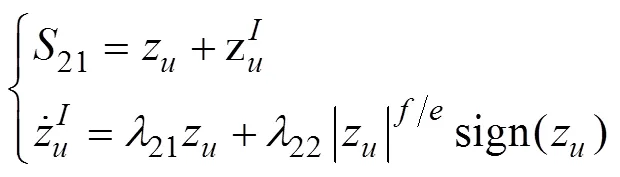
对式(25)求时间的1阶导数, 并将式(23)带入, 得

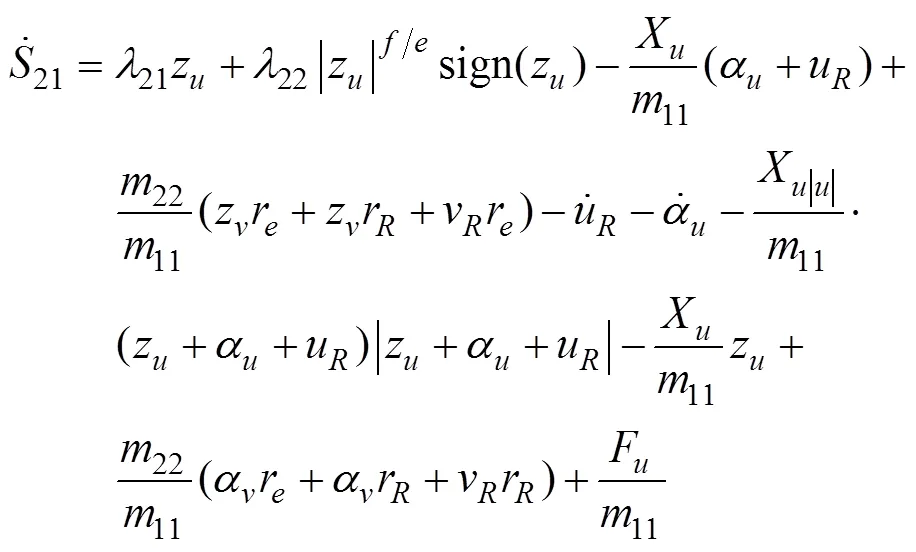
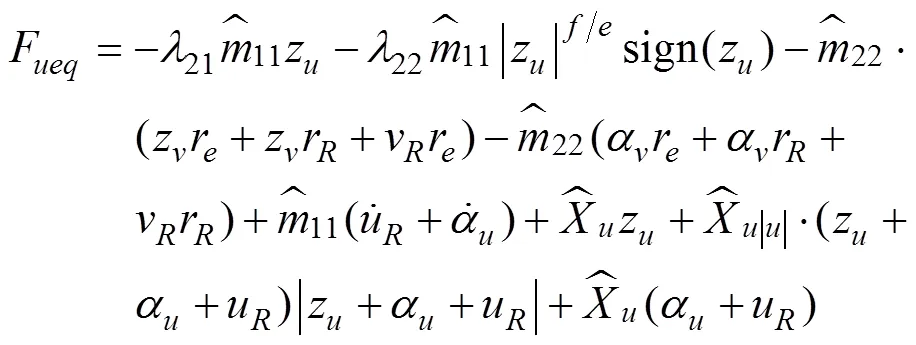
式中: “^”表示欠驱动UUV的标称水动力系数, 可通过实船试验法、自航船模法和约束船模试验法获得。

然而, 在系统参数摄动条件下, 等效控制律并不能保证得到良好的控制品质, 所以需引入趋近律进行补偿。纵向速度控制器的补偿趋近律形式为

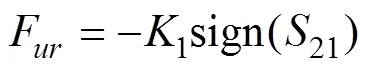
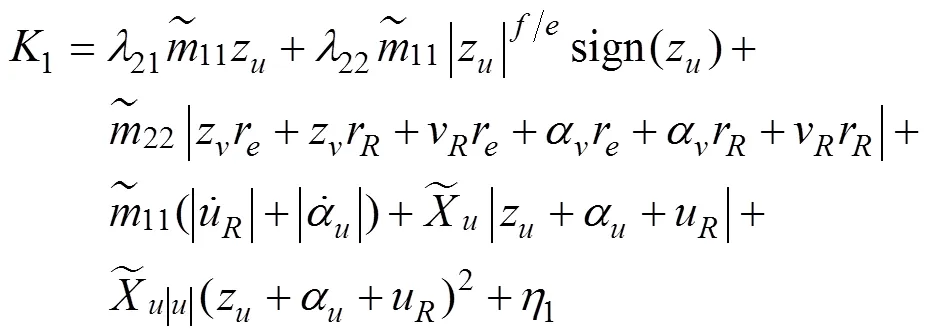
于是航行器的纵向速度控制器为

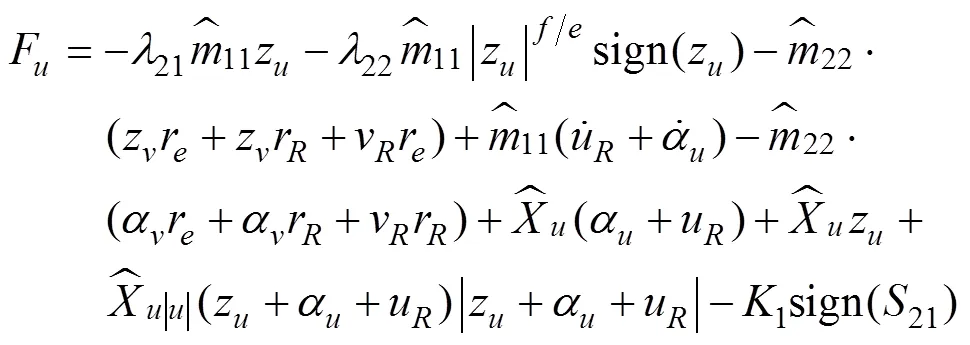
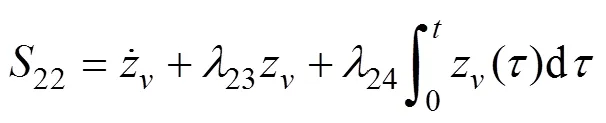
同理, 为改善控制品质, 偏航角速度补偿趋近律取如下形式

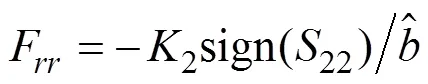
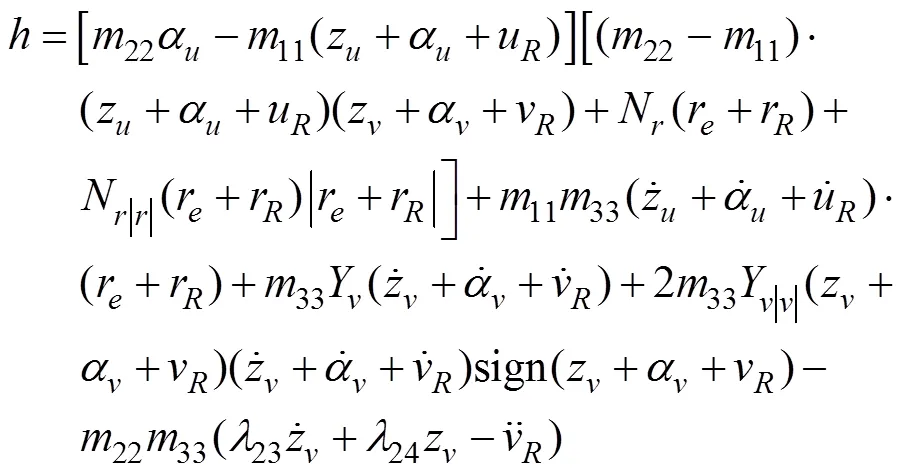
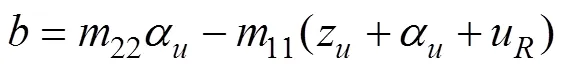
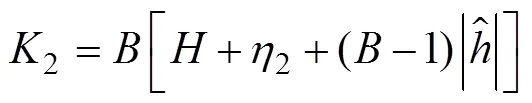
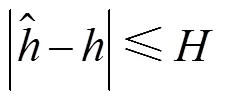
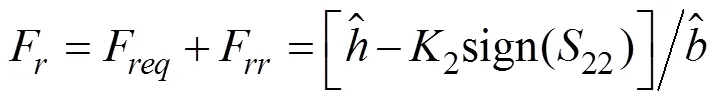
3 稳定性分析

对于式(10), 考虑如下正定形式的Lyapunov函数

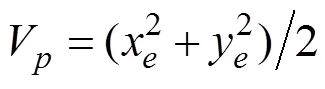
可见, 在式(19)的作用下, 位置误差能够收敛到原点。

对于式(22)分别考虑如下正定形式的Lyapunov函数

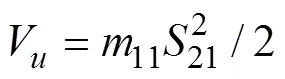
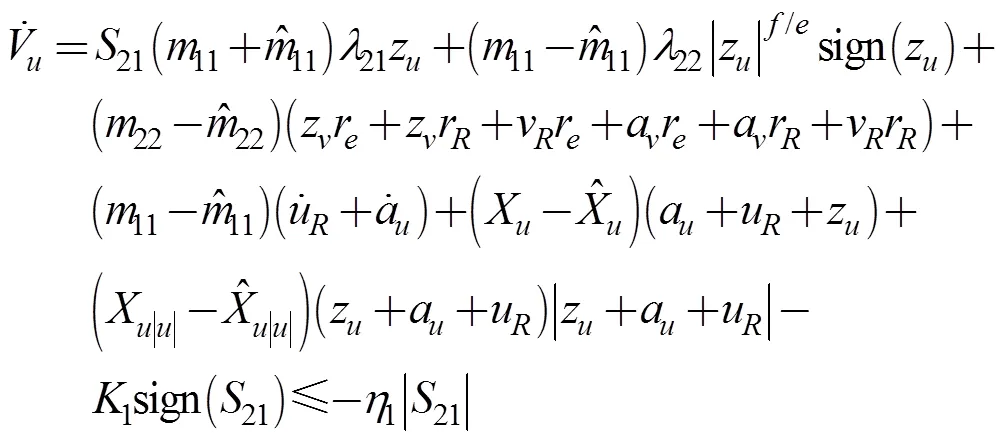
取如下形式的Lyapunov函数

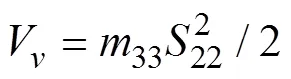
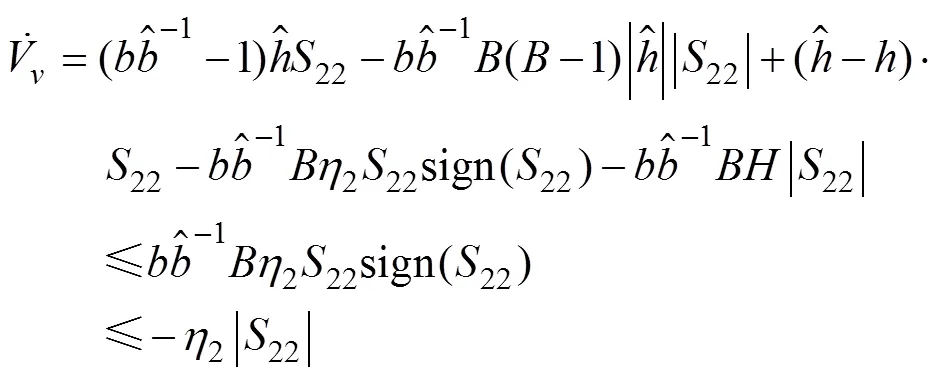
UUV运动控制系统级联表示形式如下

4 仿真结果及分析

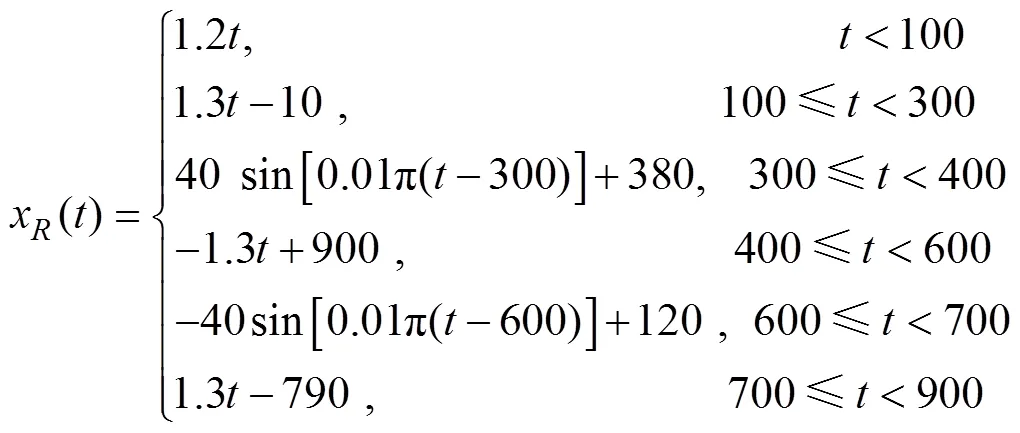
仿真结果如图2~5所示, 图2实线表示由式(42)和式(43)所定义的期望轨迹, 点划线表示欠驱动UUV在轨迹跟踪控制器式(17)、(27)、(34)作用下的实际运动轨迹。图3表示跟踪误差, 由图2和图3可以得到, 欠驱动UUV在轨迹跟踪控制器的作用下可以快速平收敛到期望轨迹。

图2 参考轨迹和实际轨迹

Fig. 2 The referential and actual trajectories

欠驱动UUV的速度误差曲线如图4所示。由于UUV初始状态静止, 可以得到UUV纵向速度误差和横向速度误差在初始阶段最大。

欠驱动UUV的轨迹跟踪控制输入曲线见图5。初始阶段因初始位置误差较大, 控制力和力矩曲线变化剧烈, 进入稳定段后控制力和力矩变得平缓, 在轨迹的过渡处力和力矩产生明显变化。

5 结论

针对欠驱动UUV平面轨迹跟踪控制问题, 采用积分滑模控制策略, 经仿真试验可知控制器有如下优点:

1) 通过引入1阶积分滑模面设计了速度控制器, 并运用Lyapunov稳定理论证明了位置误差和速度误差能够收敛到原点;

2) 针对航行器参数摄动问题进行仿真, 从仿真结果看出, 积分滑模控制方法在航行器参数摄动情况下对欠驱动UUV平面轨迹跟踪是有效的, 能够实现较精确跟踪控制,达到预期目的。

此外在跟踪直线段轨迹时由偏航角误差可以看到, 并没有出现舵角持续激励的现象, 说明该控制器可同时跟踪直线和弧线轨迹。

[1] 徐玉如, 肖坤. 智能海洋机器人技术进展[J]. 自动化学报, 2007, 33(5): 518-521.Xu Yu-ru,Xiao Kun.Technology Development of Auto- nomous Ocean Vehicle[J].Automatica,2007, 33(5): 518-521.

[2] 郭晨, 汪洋, 孙富春, 等. 欠驱动水面船舶运动控制研究综述[J]. 控制与决策, 2009, 24(3): 321-329.Guo Chen, Wang Yang, Sun Fu-chun, et al. Survey for Motion Control of Underactuated Surface Vessels[J]. Control & Decision, 2009, 24(3): 321-329.

[3] Fossen T I. Handbook of Marine Craft Hydrodynamics and Motion Control[M]. USA: Wiley, 2011.

[4] Wan L, Sun N, Liao Y L. Backstepping Control Method for the Trajectory Tracking for the Underactuated Autonomous Underwater Vehicle[J]. Advanced Materials Research, 2013, 798-799: 484-488.

[5] Repoulias F, Papadopoulos E. Planar Trajectory Planning and Tracking Control Design for Underactuated AUVs[J]. Ocean Engineering, 2007, 34(11-12): 1650-1667.

[6] Repoulias F, Papadopoulos E. Trajectory Planning and Tracking Control of Underactuated AUVs[C]//IEEE International Conference on Robotics and Automation. Bar- celona: IEEE, 2006: 1610-1615.

[7] 贾鹤鸣, 张利军, 程相勤, 等. 基于非线性迭代滑模的欠驱动UUV三维航迹跟踪控制[J]. 自动化学报, 2012, 38(2): 308-314.Jia He-ming, Zhang Li-jun, Cheng Xiang-qin, et al. Three-dimensional Path Following Control for an Under- actuated UUV Based on Nonlinear Iterative Sliding Mode[J]. Automatica, 2012, 38(2): 308-314.

[8] Yu R, Zhu Q, Xia G, et al. Sliding Mode Tracking Control of an Underactuated Surface Vessel[J]. Iet Control Theory & Applications, 2012, 6(3): 461-466.

[9] Qiao L, Yi B, Wu D, et al. Design of Three Exponentially Convergent Robust Controllers for the Trajectory Tra- cking of Autonomous Underwater Vehicles[J]. Ocean Engineering, 2017, 134: 157-172.

[10] Elmokadem T, Zribi M, Youcef-Toumi K. Terminal Sliding Mode Control for The Trajectory Tracking of Underactuated Autonomous Underwater Vehicles[J]. Ocean En- gineering, 2016, 129: 613-625.

[11] 徐健, 汪慢, 乔磊, 等. 欠驱动UUV三维轨迹跟踪的反步动态滑模控制[J]. 华中科技大学学报(自然科学版), 2015, 43(8): 107-113. Xu Jian, Wang Man, Qiao Lei, et al. Backstepping Dynamical Sliding Mode Controller for Three-Dimen- sional Trajectory Tracking of Underactuated UUV[J]. Journal of Huazhong University of Science & Technology, 2015, 43(8): 107-113.

[12] Wang H J, Chen Z Y, Bian X Q, et al. Robust Adaptive Path Following Control for Autonomous Underwater Ve- hicles with Virtual Guidance[C]//Control Conference. He fei: IEEE, 2012: 4283-4288.

[13] 夏国清,杨莹,赵为光. 欠驱动AUV模糊神经网络2增益鲁棒跟踪控制[J]. 控制与决策, 2013, 28(3): 351-356. Xia Guo-qing, Yang Ying, Zhao Wei-guang. FNN-based2Following Control of Underactuated Autonomous Un- derwater Vehicles[J]. Control & Decision, 2013, 28(3): 351-356.

[14] 贾鹤鸣, 张利军, 齐雪, 等. 基于神经网络的水下机器人三维航迹跟踪控制[J].控制理论与应用, 2012, 29(7): 56-62. Jia He-ming, Zhang Li-jun, Qi Xue, et al. Three- dimensional Path Tracking Control for Autonomous Underwater Vehicle Based on Neural Network[J]. Control Theory & Applications, 2012, 29(7): 56-62.

[15] Zhou J, Ye D, He D, et al. Three-Dimensional Trajectory Tracking of an Underactuated UUV by Backstepping Control and Bio-Inspired Models[C]//Chinese control conference. Dalian: IEEE, 2017: 966-972.

[16] 严浙平, 段海璞. UUV航迹跟踪的双闭环Terminal滑模控制[J]. 中国舰船研究, 2015, 10(4): 112-117. Yan Zhe-ping, Duan Hai-pu. A Double Closed-Loop Terminal Sliding Mode Controller for the Trajectory Tra- cking of UUV[J]. Chinese Journal of Ship Research, 2015, 10(4): 112-117.

[17] 李殿璞. 船舶运动与建模[M]. 北京: 国防工业出版社, 2008.

[18] 贾鹤鸣. 基于反步法的欠驱动UUV空间目标跟踪非线性控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.

[19] Ross S. An Elementary Introduction to Mathematical Finance Options and Other Topics[M]. Beijing: China Ma- chine Press, 2004.

[20] Huang X, Lin W, Yang B. Global Finite-Time Stabilization of a Class of Uncertain Nonlinear Systems[J]. Au- tomatica, 2005, 41(5): 881-888.

(责任编辑: 陈 曦)

Trajectory Tracking Control Method for Underactuated UUV Using Integral Sliding Mode under Parameter Perturbation

YAN Zhe-ping1, LI Xiang1, SONG Yu-wu2, LI Juan1, 3

(1. College of Automation, Harbin Engineering University, Harbin 150001, China; 2. Theory Training Department of Harbin Air Force Flight Academy, Harbin 150001, China; 3. Science and Technology on Underwater Vehicle Technology, Harbin Engineering University, Harbin 150001, China)

A horizontal plane trajectory tracking control problem of an underactuated unmanned undersea vehicle(UUV) is discussed considering parameter perturbation. A control strategy based on backstepping method and integral sliding mode control method is hence proposed. The trajectory tracking error equation is established using the motion characteristics of the UUV. Employing the backstepping method and the integral sliding mode control method, the first-order integral sliding mode vertical velocity controller and yaw velocity controller are designed to realize the horizontal plane trajectory tracking with parameter perturbation, and the stability of the system is proved. Simulation results show that the proposed trajectory tracking control method can effectively complete trajectory tracking task, and is rather robust to parameter perturbation.

underactuated UUV; trajectory tracking; parameter perturbation; integral sliding mode control; backstepping method

严浙平, 李响, 宋育武, 等. 参数摄动下基于积分滑模的欠驱动UUV轨迹跟踪控制方法[J]. 水下无人系统学报, 2018, 26(3): 200-206.

TJ630.33; TP242

A

2096-3920(2018)03-0200-07

10.11993/j.issn.2096-3920.2018.03.003

2016-11-19;

2016-12-18.

国家自然科学基金(51679057, 51609046)、水下机器人技术重点实验室研究基金(614221502061701).

严浙平(1972-), 男, 教授, 博导, 研究方向为无人水下航行器的总体设计、智能控制和运动控制.