基于数值波浪水槽的圆柱浮标运动仿真与分析

杨壮滔, 张 涛, 段 浩, 朱 敏



基于数值波浪水槽的圆柱浮标运动仿真与分析

杨壮滔, 张 涛, 段 浩, 朱 敏

(中国船舶重工集团公司 第705研究所昆明分部, 云南 昆明, 650106)

研究了不同海况条件下外形及重浮心距对圆柱形浮囊浮标运动响应的影响规律。使用雷诺平均的N-S方程(RANS)和流体体积模型(VOF), 基于势流粘流相结合的方法, 建立了数值波浪水槽。对比分析了不同物理时间下所造波的波形与理论波形, 结果表明, 该方法的造波精度满足工程应用需求。同时结合6自由度(6DOF)模型和重叠网格方法, 在不同海况作用下对2种类型浮标的运动特性进行仿真。结果表明, 文中所建立的浮标运动仿真分析方法是正确有效的, 文中所做工作可为圆柱形浮囊浮标设计提供参考。

圆柱形浮标; 数值波浪水槽; 6自由度模型; 运动特性

引言

小型浮标在军用和民用领域的应用前景日益广阔。但由于尺寸小, 质量轻, 容易受海浪海流的影响, 产生较为剧烈的运动。浮标在海浪的作用下会产生6自由度运动(six degrees of freed- om, 6DOF), 分别为纵荡(surge)、横荡(sway)、垂荡(heave)、横摇(roll)、艏摇(yaw)、纵摇(pitch)运动, 从而对其工作造成不利影响, 因此需要对浮标运动响应进行研究, 以指导其外形设计[1]。

与其他形状浮标相比, 圆柱型浮标受到波浪激励的影响最小。因此小型浮标的形体多选用圆柱形[2]。工程上常用Morison方程对浮标在波浪激励下的运动特性进行仿真分析[3]。1977年, Berteaux等[4]使用该方法研究分析了圆柱形浮标的运动特性。2010年, 曲少春等[2]使用该方法对圆柱形浮标进行运动特性分析得出对该型浮标改进的建议。Morison方程是一种基于势流理论的方法, 无法求解波浪遇到浮标后发生的绕射、越浪、破碎、爬高和涡旋等现象带来的影响[5]。

随着计算机技术的发展, 基于雷诺平均的N-S方程(reynolds averaged navier-stokes, RANS)方法的数值波浪水槽能有效求解波浪遇到物体后发生的绕射等现象带来的影响, 在船舶耐波性分析领域应用较广, 也可用于研究圆柱形浮标在海浪激励下的运动特性研究[6]。在相同波浪激励作用下, 圆柱形浮标的运动特性受其外形和重浮心距影响较大, 但暂无相关研究报道。因此, 文中将使用数值波浪水槽对2种浮囊类型和不同重浮心距的圆柱形浮标在波浪作用下的运动特性进行对比分析, 总结垂荡和纵摇规律, 为圆柱形浮标提供参考设计。

1 数值方法

1.1 计算方法

对于不可压非定常粘性流体, RANS方法是目前工程上常用的计算流体力学(computatio- nal fluid dynamics, CFD)方法之一。其中, 空间离散采用有限体积法, 时间推进采用双时间法。该方法的连续性方程和动量方程可写为

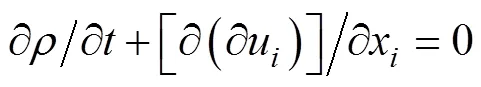
在数值造波时, 需要跟踪气体和液体的界面。因而选用流体体积(volume of fluid, VOF)方法处理气体和液体的界面跟踪问题, 该方法跟踪界面是通过求解相连续方程实现的[8]。且

1.2 重叠网格与6DOF模型

文中使用CFD方法求解波浪作用下浮标运动响应, 在计算中, 浮标姿态随时间变化而变化。由于不同姿态下所计算出的压力分布不同, 为了准确求解浮标在不同姿态下所受到的力和力矩, 需要使用6DOF模型来求解浮标的姿态变化。文中选用重叠网格法来实现计算中的浮标运动[9]。

如图1所示, 该方法的网格分为重叠区域和背景区域, 背景区域为整个计算域, 重叠区域为包含求解对象的运动区域。在计算时, 2个区域将进行数据传递和数值差分, 利用重叠区域相对背景区域发生的运动来反应求解对象发生的运动。在划分网格时, 需对2个区域交界处网格进行控制, 使得在交界处2个区域的网格尺寸保持一致。

建立运动区域后, 需要使用6DOF模型来实现运动区域在流体作用力下的运动计算。该模型将求解对象视为刚体。将其动量方程和动量矩方程对时间求导, 得

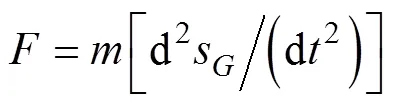
将式(4)和式(5)展开成3个方向可得

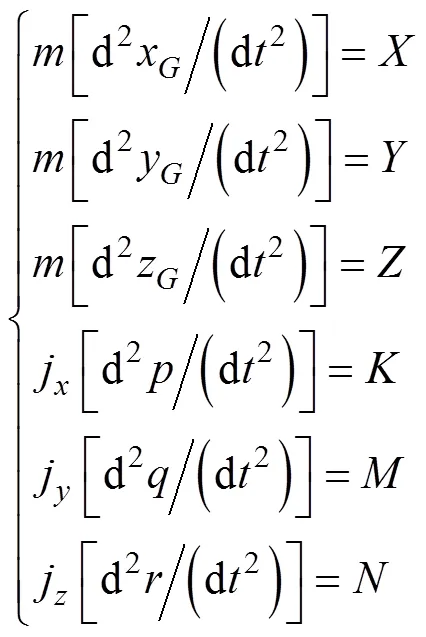
求解流程如图2所示。

2 数值水槽造波

2.1 造波方法

文中的数值仿真在一个3D数值水池中进行, 该数值水池以RANS方法和多相流模型为基础。对小型浮标在波浪作用下的运动进行仿真时, 首先需要生成满足计算要求的波浪。在数值仿真中, 从机理上常见的造波方法可分为2类: 源造波法和边界造波法。源造波法主要包括质量源造波和动量源造波, 边界造波法主要包括推板造波、摇板造波、楔形冲箱造波等模拟物理模型的方法以及边界流体流动速度函数的直接输入法[10]。

文中使用的造波方法为边界流体流动速度函数的直接输入法。根据线性理论, 波面方程和速度场表达式分别为

若采用纯粘性流的计算方法, 数值水槽出口处需要增加阻尼区域以防止波浪在出口边界处发生反射。由于仿真所需物理时间较长, 出口处的阻力会引起波浪幅值的衰减。因此使用不需要阻力区域的势流与粘流相结合的方法来进行造波, 该方法计算区域分为势流方法区域和粘流方法区域2部分。如图3所示, 势流区域将粘流区域包裹住, 粘流区域在波浪传播方向的长度等于2个波长, 宽为1个波长, 浮标模型位于此区域。势流区域的外边界到粘流区域与势流区域的交界的距离也分别为2个波长。因此, 文中所建立的数值造波水池沿波浪传播方向长度等于6个波长, 宽度等于5个波长。由于出口边界为流体流动的速度函数, 因此不需要消波阻尼区域来防止出口反射, 且生成的波浪幅值不会因阻尼的存在而随物理时间衰减。

2.2 造波精度验证

仿真中使用线性规则波作为波浪输入。为真实反映海况, 采用有意波高作为规则波的波高输入。2~5级海况波高周期如表1所示。

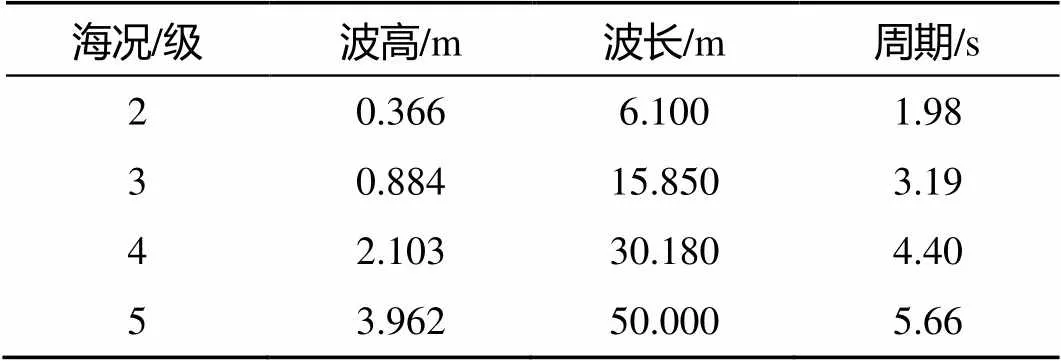
表1 不同海况下波浪参数

分别选取以2级海况为目标所造的波形图与理论值进行比较, 波面方程见式(7), 波长为6.1 m, 波高为0.366 m, 周期约为1.98 s。为验证在反应浮标运动响应的时间范围内所造波浪的精度, 分别取第0 s、10 s、30 s和50 s的波形进行对比。

图4中, 刚开始造波时2种方法所造的波形与理论波形一致, 随着计算物理时间的推移(见图5~图7), 由于纯粘流造波方法需要在数值水槽出口处加阻尼, 导致出口处波幅开始衰减。

计算的物理时间越长, 波幅的衰减越大, 甚至出现波长发生改变的状况。对于势流与粘流相结合的方法, 由于在出口处不需要消波阻尼, 因此不会使波幅发生衰减(见图4~图7), 只会因数值计算带来较小误差, 对浮标在波浪作用下运动响应的求解影响较小。因此使用势流和粘流结合的方法进行数值造波, 精度满足工程实际需求。

3 浮标运动仿真结果与分析

3.1 仿真条件

对质量和浮囊排水体积相同, 浮囊外形不同的2种浮标进行仿真。为了控制仿真输入值, 选用单方向规则波作为输入波, 由于浮标和水槽是对称的, 因此选用垂荡幅值、纵摇幅值和纵摇极值作为浮标响应输出值。其中: 垂荡幅值能反映浮标竖直方向运动的位移量和速度; 纵摇幅值能反应浮标定轴转动的角速度; 纵摇极值能反映浮标定轴转动的旋转角度。浮标主视图如图8所示, 其中左图浮标浮囊为扁平形, 简称扁平型浮标, 右边浮标浮囊为细长形, 简称细长型浮标。浮标参数如表2所示。建立3套坐标系, 如图9所示, 分别为浮标坐标系和大地坐标系。规定静水面与浮标轴线相交的交点为大地坐标系的原点,轴垂直于水平面方向向上,轴方向指向波浪传播方向,轴垂直于、轴向外。

表2 浮标的物理参数

图8 浮标主视图

Fig. 8 Main view of buoy

由于浮标在水面运动使得浮标排水实时变化, 导致其浮心位置随着浮标运动而发生变化。在仿真中, 将浮标视为刚体且质量和质量分布不发生变化, 因此选用浮标质心作为浮标坐标系的坐标原点O,z轴垂沿浮标轴线方向向上, 当浮标漂浮在静止水面时,x轴和y轴与大地坐标系的轴和轴指向一致。在运动过程中, 浮标的平移响应由浮标坐标系和大地坐标系的相对位移来表示, 浮标的转动响应由2套坐标系坐标轴的相对夹角来表示。

输入波形条件, 对不同浮标进行仿真, 并监测波面图, 如图10和图11所示。直到输出运动响应值呈周期性变化, 则取30 s的稳定周期内的输出值作为结果。由于该仿真得到的结果是时励曲线图, 为了较为明显地反映出浮标在波浪影响下的响应情况, 取浮标运动稳定后位移幅值的平均值作为垂荡响应幅值。

3.2 垂荡运动仿真结果与分析

如图12所示, 浮标的垂荡运动幅值受海况和浮囊外形影响较大, 总体上随着海况等级的增加而增加。在相同的海况和重浮心距的条件下, 扁平型浮囊浮标的垂荡幅度大于细长型浮囊浮标的垂荡幅度。

图13中, 扁平型浮标的幅值响应算子(respo- nse amplitude operator, RAO)值更接近1, 而细长型浮标的RAO值小于1, 说明扁平型浮标在垂直方向受波面影响比细长型浮标大。使用理论方法对浮标在规则波作用下的运动进行分析, 进一步验证仿真所得结论。由于浮标的尺寸长度远小于波浪波长, 重量较轻, 因此采用Froude-Krylov理论将浮标所受流体的拖曳力和惯性力线性化[4]。

在垂直方向上, 浮标运动方程

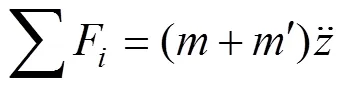
3.3 纵摇运动仿真结果与分析

如图14所示, 浮标的纵摇运动幅值受海况、浮囊外形和重浮心距的影响较大, 总体上也随海况等级的增加而增加。在相同的海况和重浮心距的条件下, 若海况等级较低, 细长型浮标的纵摇幅值低于扁平型的; 若海况等级较高, 则细长型浮标的纵摇幅值高于扁平型的。在相同浮标外形和海况的情况下, 浮标的纵摇幅值不随重浮心距增大而减小。图14中, 50 mm重浮心距细长型浮标在2级海况作用下较扁平型浮标小很多。

如图15所示, 当浮标在1个波峰的作用下发生偏转后姿态开始回复, 若还未回复到平衡位置时下一个波峰再次使浮标发生偏转。使得浮标运动幅度较小而极值较高。运动幅值反映了纵摇运动的速度大小, 为反映纵摇时位移量的大小需要通过纵摇运动的极值。如图16所示, 可以看出,在相同海况和重浮心距的条件下, 扁平型浮标的纵摇响应极值要小于细长型浮标的极值。

同理, 浮标绕质心纵摇的运动方程

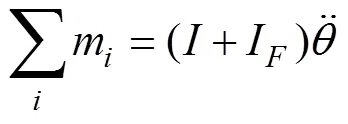
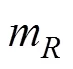
扁平型浮囊竖直横截面积较大, 当浮标偏转角度一致时, 扁平型浮囊的排水体积变化量大于细长型, 使得扁平型浮标的回复力大于细长型浮标。而扁平型浮囊的直径大, 相同排水体积下, 沾湿面积小于细长型浮囊, 使得扁平型浮标受到水平方向波浪的拖曳力较小。而当海况等级较小时, 波长较短, 相对于浮囊液面不平, 扁平型浮囊直径大, 使得浮囊左右排水体积相差较大, 造成的扰动力矩也大于细长型浮标。因此, 海况等级较低时, 细长型浮标纵摇运动的幅值较小。当海况等级较高时, 波长较长, 相对于浮囊液面较平, 浮囊左右排水体积相差较小, 造成的扰动力矩较小, 由于扁平型浮标的回复力大于细长型浮标, 受水流拖曳力小于细长型浮标, 因此海况等级较大时, 扁平型浮标纵摇运动的幅值较小。而且扁平型浮标的回复力对于细长型浮标, 受水流拖曳力小于细长型浮标, 使得其更容易回复到平衡位置, 因此扁平型浮标的纵摇极限值小于细长型浮标。

对于相同浮囊外形的浮标, 在运动中排水体积变化较小, 浮心位置变化较小, 只有通过降低重心来提高重浮心距。若重浮心距越大, 受到的回复力矩越大, 同时拖曳力对重心的力矩也越大, 故增大重浮心距不能有效减小浮标纵摇的幅度。

4 结束语

文中使用势流粘流相结合的方法进行规则波的数值水池造波, 并选取不同物理时间的波形图与纯粘流方法所造的波形图进行对比, 得出势流粘流相结合的方法所造波与理论值对比误差较小, 可以用于浮标运动的仿真计算。使用该方法造波, 对不同外形和不同重浮心距的圆柱形浮标在不同海况作用下的运动进行仿真, 得到浮标在波浪影响下运动仿真的结果, 总结垂荡和纵摇规律, 使用理论方法进行分析, 验证仿真结论可信。结论如下:

1) 浮标的垂荡运动幅值、纵摇运动幅值和极值整体上随海况等级的增加而增加;

2) 在相同海况和重浮心距条件下, 细长型浮标的垂荡运动幅值小于扁平型浮标。

3) 在相同海况和重浮心距条件下, 细长型浮标的纵摇运动姿态角极限值大于扁平型浮标;

4) 相同重浮心距条件下, 低等级海况下细长型浮标的纵摇运动幅值小于扁平型浮标, 而高等级海况下细长型浮标的纵摇运动幅值大于扁平型浮标;

5) 在相同海况和外形的条件下, 重浮心距越大, 浮标的横摇幅值不一定越大。

文中所得结论可以在浮标耐波性设计中起指导性作用, 探究如何削减浮标运动响应带来的不利影响将是下一步研究方向。

[1] 戴洪磊, 牟乃夏, 王春玉, 等. 我国海洋浮标发展现状及趋势[J]. 气象水文海洋仪器, 2014, 31(2): 118-121, 125.Dai Hong-lei, Mou Nai-xia, Wang Chun-yu, et al. Deve- lopment Status and Trend of Ocean Buoy in China[J]. Me- teorological, Hydrological and Marine Instruments, 2014, 31(2): 118-121, 125.

[2] 曲少春, 郑琨, 王英民. 圆柱形浮标运动分析与仿真[J].计算机仿真, 2010, 27(6): 363-367.Qu Shao-chun, Zheng Kun, Wang Ying-min. Analysis and Simulation of Spar Buoy Motion[J]. Computer Simulation, 2010, 27(6): 363-367.

[3] 王树青, 梁丙臣. 海洋工程波浪力学[M]. 青岛: 中国海洋大学出版社, 2013.

[4] Berteaux H O, Goldsmith R A, Schott III W E. Heave and Roll Response Of Free Floating Bodies Of Cylindrical Shape: WHOI-77-12[R]. Leipzig, Germany: International Transport Fouum, 1977.

[5] 孙斌. 波浪作用下玻璃钢浮标水动力特性的数值分析[D]. 长沙: 长沙理工大学, 2011.

[6] 唐歆. 海洋资料浮标水动力分析及结构研究[D]. 上海: 上海海洋大学, 2012.

[7] 马峥, 黄少锋, 朱德祥. 湍流模型在船舶计算流体力学中的适用性研究[J]. 水动力学研究与进展, 2009, 24(2): 207-216.

[8] Ma Zheng, Huang Shao-feng, Zhu De-xiang. Study on Applicability of Turbulence Model in Ship Computational Fluid Dynamics[J]. Chinese Journal of Hydrodynamics, 2009, 24(2): 207-216.

[9] Hirt C W, Nichols B D. Volume of Fluid(VOF) Method for the Dynamics of Free Boundary[J]. Journal of Comp- utational Physics, 1981, 39(1): 201-225.

[10] 赵发明, 高成君, 夏琼. 重叠网格在船舶CFD中的应用研究[J]. 船舶力学, 2011, 15(4): 332-341.Zhao Fa-ming, Gao Cheng-jun, Xia Qiong. Overlap Grid Research on the Application of Ship DFD[J]. Journal of Ship Mechanics, 2011, 15(4): 332-341.

[11] 方昭昭, 朱仁传, 缪国平, 等. 基于数值波浪水池的波浪中船舶水动力计算[J].水动力学研究与进展, 2012, 27(5): 515-524.Fang Zhao-zhao, Zhu Ren-chuan, Miao Guo-ping, et al. Numerical Calculation of Hydrodynamic Forces for a Ship in Regular Waves Bsed on Numerical Wave Tank[J]. Chinese Journal of Hydrodynamics, 2012, 27(5): 515-524.

(责任编辑: 杨力军)

Simulation and Analysis of Cylindrical Buoy Motion Based on Numerical Wave Flume

YANG Zhuang-tao, ZHANG Tao, DUAN Hao, ZHU Min

(Kunming Branch of the 705 Research Institute, China Shipbuilding Industry Corporation, Kunming 650106, China)

The influences of a buoy’s shape and gravity center distance on its motion response in different sea conditions are studied. Using the Reynolds-averaged Navier-Stokes equations(RANS) and the volume of fluid(VOF) model, a numerical wave flume is established via combination of potential flow and viscous flow. The waveform generated by this numerical wave flume and the theoretical waveforms are analyzed for different physical time, and the results show that the accuracy of the generated waveform satisfies engineering application. In addition, the six degrees of freedom (6DOF) model and the overlap grid method are employed to simulate the motion characteristics of two kinds of buoys in different sea conditions. It is shown that the present buoy motion simulation and analysis method is correct and effective. This study may facilitate the design of cylindrical buoys.

cylindrical buoy; numerical wave flume; six degrees of freedom(6DOF) model; motion characteristic

杨壮滔, 张涛, 段浩, 等. 基于数值波浪水槽的圆柱浮标运动仿真与分析[J]. 水下无人系统学报, 2018, 26(3): 207-213.

TJ67; TB71.2

A

2096-3920(2018)03-0207-07

10.11993/j.issn.2096-3920.2018.03.004

2017-10-18;

2017-12-19.

杨壮滔(1993-), 男, 在读硕士, 主要研究方向为水中兵器总体设计.