细长杆用于超音速飞机降噪的数值分析

翟荣华，周华

(同济大学 航空航天与力学学院，上海 200092)

细长杆用于超音速飞机降噪的数值分析

翟荣华，周华

(同济大学 航空航天与力学学院，上海 200092)

在超音速飞机头部加装合理设计的细长杆可有效降低飞行噪音。基于Fluent准三维数值模拟手段对多组细长杆设计方案进行模拟分析，对比其对远场压力的影响，以比较各类细长杆的降噪效果，根据气动理论对数值结果作出解释，揭示细长杆的降噪效果与其外形的内在联系；从远场压力最大值、远场压力曲线形状等不同方面分析细长杆对音爆的影响。结果表明：6 m长的12.5°半锥角单级锥形细长杆有明显的降噪效果；合理设计的多级细长杆可明显降低初始过压值，并能延迟远场压力达到最大值的时间；凹凹面、凹锥面、凸凹面和凸锥面的细长杆能够降低远场压力峰值，改善压力曲线的形状，具有较好的降噪作用；细长杆产生的强膨胀波能在激波传播过程中大幅削弱机头激波，从而削弱音爆水平。

超音速飞机；细长杆；降噪；音爆；N波

0 引 言

根据超音速空气动力学，飞机在超音速巡航时引起的大气压力扰动倾向于合并成一个N波。最大扰动和最强激波出现在机身中后部的某个位置，该处的横截面积接近最大值且绝大部分升力由此处产生。强激波比前机身头部产生的弱激波具有更陡的激波角，随着扰动从机体开始传播，最陡的激波逐渐合并了其之前的所有扰动，形成强激波；其后的流动开始膨胀，在无精细塑形的情况下，随后的扰动合并入尾激波。激波的厚度很小，经过激波后空气的压强、密度、温度都急剧升高，速度急剧下降。被飞机的两道激波波及的任何空间和物体均会感觉到这种强烈变化,反映到地面行人的耳朵里，耳膜感受到突然的气压变化——两声巨响，即音爆[1]。超音速飞机的飞行噪声主要来自其飞行时产生的音爆现象。在超音速飞机的设计中，如何解决音爆问题已成为决定和衡量设计方案的关键技术指标之一，探索降低音爆水平的相关技术具有重要意义。

为了减弱音爆带来的噪声问题，国内外先后提出了多种技术手段用于降低气动噪声，主要分为航迹优化和改变气动外形两大类方法。航迹优化是指将航线设计到无人区上空并增加起飞/着陆时的飞行角度以减小受影响的区域；改变气动外形是指通过改变飞机的尺寸、优化气动外形或加装降噪装置三种途径，降低飞机对空气的扰动，改变激波的形状和强度，从而达到减弱音爆的目的。

传统的低音爆技术致力于钝化飞机机头[2-4]以增强弓形激波，使激波更陡，从而延缓压力波的合并，该技术的主要缺点是钝型机鼻会增加飞行阻力。湾流公司的研究指出，飞机选取合适的有效面积分布，可使其展示出良好的低音爆特性，并初步得到0.3 psf首激波的过压要求[5]。减少飞机头部的有效面积虽然可以得到弱化的首激波，但该方法是以牺牲前机身尺寸为代价的，且对机身形状限制较大。

弱化机头激波和阻止激波合并对降低音爆噪声等级具有重要作用，是降噪的主要技术途径。P.A.Henne等[6]提出一种“静音锥(Quiet Spike)”的低音爆概念设计，通过在机头处设置一根可伸缩的静音锥来产生一系列弱激波，从而达到降低音爆的目的，但相关报道只笼统地介绍了静音锥的长度约为飞机长度的三分之一，并未给出设计细节及设计依据。传统的音爆计算方法包括CFD模拟，或者先通过风洞试验得到模型的近场解，再采用诸如波形参数法[7]、TRAPS[8]、Moc[9]、PCBoom3[10]、PCBoom4、CABoom[11]等音爆程序计算远场音爆，最后将二者的结果相结合。该方法计算量虽小，但其多用于超音速流，且不能处理脱体激波，在较低超音速、机身有较陡斜面时易失败，即该方法在考虑激波之间、激波与膨胀波系之间的干涉作用时效果不佳；由于采用不同的数值方法求解近场、远场流场，所得结果也不具有很好的说服力。

本文在国内外已有降噪方法的启发下，尝试在机头处加装类似静音锥的细长杆来降低音爆，采用不同长度、不同锥角、不同级数、不同形状的细长杆，通过CFD方法对音爆机理和细长杆参数影响进行研究；利用CFD方法直接模拟中远场，并对比各方案的远场压力波形；同时，采用统一的算法和格式求解近场和远场，采用自适应网格达到网格收敛性，使结果更具说服力。

1 数值模型

湾流公司与NASA合作的静音锥实验是在F-15B上进行的[12]，F-15B的主要参数如表1所示。飞机在做超音速飞行时，对于远场的影响近似于一个与其面积分布相同的旋成体，本文也选取F-15B作为基本模型，模拟其飞行环境和形状，并将其简化为主要几何参数相同的细长旋成体(基本模型简化为旋成体的参数如表2所示，简化结构如图1所示)，以便后期将音爆计算流场转化为准三维问题求解，缩短计算时间。

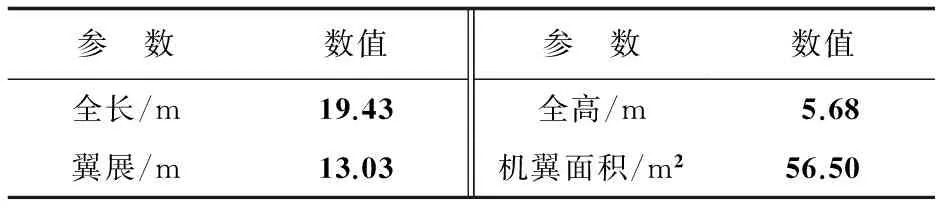
表1 F-15B的主要参数

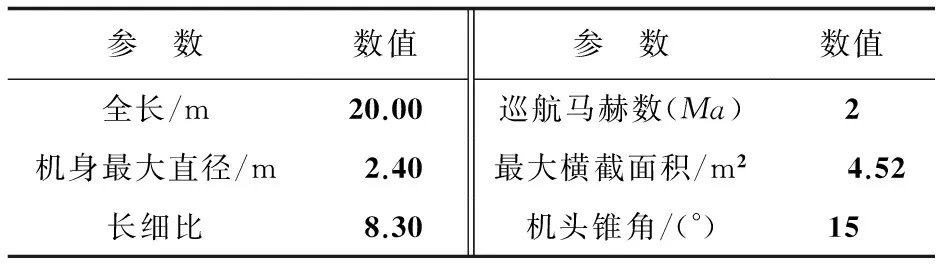
表2 基本模型简化为旋成体的参数

计算选择的飞行马赫数为2，首先进行网格划分以预估激波范围、确定计算域；然后对计算域划分结构网格。采用密度基定常求解器求解全流场，采用理想气体模型，粘度满足Sutherland关系，使用S-A湍流模型以及压力远场边界条件，以隐式格式进行计算，采用二阶迎风格式提高精度。

以压力梯度作为变量，应用自适应性加密方法对激波附近进行网格加密，再重复计算。反复计算过程中，观察网格数量对计算结果的影响，以验证网格无关性。以长度为2.00 m的锥形细长杆为例，初始网格数量为11万，计算过程中，沿压力梯度应用自适应网格进行加密处理，如图2所示，逐步增加网格数量，观察网格数量对远场压力形状的影响。不同网格密度下的远场压力如图3所示，可以看出：当网格加密到40万时，网格数量对计算结果的影响可以忽略。

2 设计方案

远场的激波一般是由近场的激波在传播过程中叠加融合而成，因此远场音爆主要取决于细长杆产生的激波和机头产生的激波的传播和叠加形式。

激波形状主要由飞行马赫数和锥角决定。细长杆降噪的机理是通过改变头部激波形状，进而改变头部激波强度，或在传播过程中阻止激波合并，从而改变远场压力波形。本文研究单级细长杆、多级细长杆、不同锥角的细长杆、连续压缩型细长杆以及流线型细长杆等不同类型的细长杆的降噪效果，并从距离飞机高度20和300 m处观察近场和远场压力曲线的演化。

过压峰值是远场N波的主要参数，也是衡量音爆大小的重要变量。噪音的本质是空气中的压力脉动，可以利用远场最大过压值的声压级降低值来量化各类细长杆的降噪效果。

采用经验公式(式(1))来衡量降噪效果：

(1)

式中：pmax为远场压力最大峰值；p0max为无细长杆方案(基本模型)的远场的过压峰值。

3 无细长杆和有细长杆近场比较

为了得到细长杆对基本模型压力场的影响，以凹凸连续型细长杆为研究对象，比较加装了该细长杆的方案和未加装细长杆的方案的近场波系及流场变化。在距离飞机20 m截面处，两种方案的近场压力曲线和压力场云图分别如图4～图5所示，可以看出：无细长杆方案有单个波峰，加装细长杆后，机头激波分裂成两个激波，形成几个较小的波峰；无细长杆方案在近场激波比较强，加装细长杆后，单独的强激波被分解为几个较弱的激波，降低了激波的强度，同时降低了近场噪音。

实际飞机不会出现尾部压强凸起，但模拟结果却出现了，其原因是实际飞机机身后半段和基本模型的准三维轴对称体差异较大，实际飞机由于垂尾的存在，使得机尾激波较弱，且偏转角大，故不会引起尾部波形凸起；而数值模拟的尾部激波较强，会引起压力波形在此处压力剧增，导致出现尾部压强凸起。虽然采用准三维模型在机身后半段出现了误差，但细长杆安装于机头部位，属于机身前段，对远场压力波形的主要部分影响较小，故采用数值模拟方法比较各种细长杆方案的降噪效果仍然具有可信性。

4 细长杆长度的影响

将头部锥形与圆柱面衔接即构成最简单的细长杆模型，选取不同长度的该形状细长杆分别进行模拟计算，以比较细长杆长度对降噪效果的影响，不同长度细长杆远场最大过压值的比较如图6所示。为了从理论上保证细长杆激波与机头激波平行，令细长杆模型的锥角与机头锥角保持一致(12.5°)，传播过程中，机头激波与细长杆激波各自发展，干涉作用弱，不易合并。

从图6可以看出：单级细长杆远场最大压力位置一致，采用单级锥设计，远场激波及噪音与细长杆的长度有关；横坐标为0表示未加装细长杆的基本模型，加装了长度为1 m的细长杆模型与基本模型的区别不大；长度为2～6 m的细长杆降噪效果明显，该长度范围内降噪效果随细长杆长度呈正比变化；长度为6 m的细长杆的远场压力最大值最小，降噪效果最好；长度大于6 m的细长杆降噪效果不再增强。其原因是：在合理的细长杆长度范围内，增加细长杆长度等于增加了飞机的长细比，有利于降低噪声水平。

合理长度的细长杆，产生一道弱激波，相当于对机头来流进行预压缩，使机头产生的激波减弱。不同长度细长杆的近场激波对比如图7所示。

从图7可以看出：细长杆太短，降噪效果不明显，原因是其产生的激波距离机头太近，传播过程中，细长杆产生的激波与机头激波很快合并为一道激波，不能起到降噪作用；而8 m长度的细长杆，其降噪效果不如6 m长度的细长杆，原因是细长杆产生的激波距离机头较远，细长杆产生的激波与机头激波干涉程度较弱，即细长杆对机头激波的影响较小，没有起到预压缩作用，致使降噪效果减弱。

不同长度单级细长杆的远场压力波形对比如图8所示。

从图8可以看出：细长杆长度为1～4 m时，细长杆产生的激波已合并入机头强激波中，远场波形呈N波形状，达到压力最大值所需时间较短，感官噪音较强；细长杆长度为6～8 m时，远场压力波形并非N波形状，先缓慢达到一定压力值(第一超压值)，分别为17和63 Pa，经过第二次压力跃升达到压力最大值，远场压力由标准大气压上升至最大压力值所经历的空间距离增加了4～7 m，根据该空间距离值和来流速度得到压力上升到最大值的时间增加了约6～10 ms，音爆带给路面行人的感受由短处强烈的轰鸣变为相对缓慢柔和的噪音，即降低了音爆影响。

综上所述，受长细比、飞机结构和飞行力学等限制，加装细长杆的长度不能无限制地增长。超音速飞机长细比的合理范围为10～23，细长杆的长度应使总长细比在合适的范围内，例如控制细长杆的长度在1/3机身长度之内。单级锥合适的长度范围为6～8 m，当Ma=2时，6 m长度的细长杆降噪效果最好；细长杆长度的最优值随着飞行高度和马赫数的变化而变化，在超音速飞行中，应采用可伸缩的细长杆，根据飞行高度和马赫数调节其长度，以达到最佳的音爆抑制效果[13]。

5 细长杆锥角的影响

根据可压缩流理论，Ma=2时，产生贴体斜激波的圆锥角最大为22.0°、最大激波角为65.0°。为了探究细长杆锥角对降噪效果的影响，采用半锥角分别为30.0°、25.0°、20.0°、15.0°、12.5°、10.0°、7.5°和5.0°的单级锥形细长杆进行比较，细长杆的长度统一为6 m。其中20.0°、15.0°、12.5°、10.0°和7.5°半锥角细长杆均产生贴体斜激波，且激波较弱；25.0°和30.0°半锥角细长杆则产生弓形脱体激波，且细长杆前部激波强。不同半锥角细长杆的阻力系数、降噪效果的对比如图9所示，半锥角为0°表示未加装细长杆的基本模型。不同半锥角细长杆的远场压力波形前段和近场激波分别如图10～图11所示。

从图9～图11可以看出：①细长杆的半锥角越小，其形成的激波角越小，细长杆激波与机头激波的合并越快，降噪效果越差，例如，细长杆半锥角为5.0°时，细长杆激波很快合并入机头激波中，远场压力波形呈明显的N波形状，与基本模型相比并无区别，远场压力峰值较大，压力上升时间较短，降噪效果较差；②细长杆的半锥角越大，其形成的激波角越大，即细长杆产生的激波角度更陡，在传播过程中，细长杆激波不易合并入机头激波中，同时，对来流的预压缩作用越强，使机头产生的激波越弱，另外，较陡的激波产生了较强的膨胀波，近场波系在流场中传播时，强膨胀波被机头激波吸收，进一步削弱了机头激波的强度，致使远场最大压力值大幅降低，对音爆的削弱作用较强；半锥角较大的细长杆使远场波形缓慢达到压力最大值，并非呈绝对的N波形状，即达到压力最大值的时间延长，也在一定程度上降低了音爆强度；但细长杆激波强度增强使近场阻力有所增加。

15.0°及以上半锥角的细长杆产生的激波角大于机头激波角，使细长杆产生的激波合并入机头激波的趋势降低，从而削弱了音爆强度。该原理和20世纪70年代，A.R.George等[4]提出的钝化机头以削弱音爆的方法类似，都是通过推迟激波合并，使压力波形带有多个弱激波或压力跃升，增加地面压力信号的压力上升时间；但也都存在阻力增加的弊端。10°～30°半锥角之间，由于半锥角越大细长杆激波越强，远场压力达到的首次超压值越高，时间越短。

综上所述，从细长杆对远场压力最大值、远场压力波形和近场阻力等方面综合来看，单级细长杆半锥角选择10.0°～20.0°范围较合适。其中，12.5°较好，理论上能保证细长杆激波不被机头激波快速合并，亦能达到明显的降噪效果，且不会增加太多阻力。

6 细长杆级数的影响

加装细长杆可改变远场压力分布曲线的形状，使初始超压值更小，但随后的强激波紧跟初始激波，二次超压值相对而言依然很强，音爆强度的感官感受与不加装细长杆的音爆强度相似。在单级细长杆的基础上，尝试增加细长杆的级数，使机头产生多个互相平行的弱激波，进一步改善远场压力波形。多级细长杆每一级都由一段圆锥形过渡段和圆柱面段组合而成，锥形过渡段保持平行[14]以避免每级细长杆产生的激波合并。

级数是细长杆设计的重要参数之一，单级细长杆用一道弱激波代替机头强激波，多级细长杆则可以形成多道弱激波，从理论上讲，只要这些弱激波在传播过程中能够避免相互叠加，则会进一步降低地面音爆超压值和感觉噪声级。四级细长杆的近场压力云图如图12所示，可以看出：激波之间相互平行，符合预期结果。

不同级数细长杆的模拟结果如表3所示，可以看出：相较于单级细长杆，多级细长杆的远场最大压力值略有增加。

表3 不同级数细长杆的模拟结果

不同级数细长杆的远场压力波形如图13所示，可以看出：多个弱激波混合呈近乎连续上升的姿态直到第一峰值，再经过机头激波上升到压力最大值；四级细长杆达到的第一峰值最低，原因是多级细长杆的前几级激波强度比单级细长杆更弱；四级细长杆增加了远场压力达到最大值的时间(增加了20 ms，即一个数量级)。表明，多级细长杆的主要功效是降低远场第一过压值，同时延缓达到最大压力的所需时间，因此具有更好的降噪效果，极大地衰减了音爆，使音噪更接近实际可接受的强度范围。

7 细长杆形状的影响

设置连续压缩型和流线型两种类型的细长杆，并与基本模型对比，研究不同形状的细长杆对降噪效果的影响。连续压缩型细长杆，其前端由连续的凹面构成，可产生连续的压缩波，而并非孤立的贴体激波，能够明显降低物面前端的激波大小，设计凹面衔接不同的曲面，包括锥面、凸面、凹面。流线型细长杆，其前端为上凸曲面，前部有较大锥角，后面衔接锥面或凹面，可产生较大的膨胀区。设计八种不同形状的细长杆(长度均为6 m)，并与基本模型进行对比，研究激波形状，压缩波和激波之间的相互作用，以及它们对远场噪声的影响。不同类型细长杆的形状如表4所示，它们的远场静压及降噪效果的对比如表5所示。

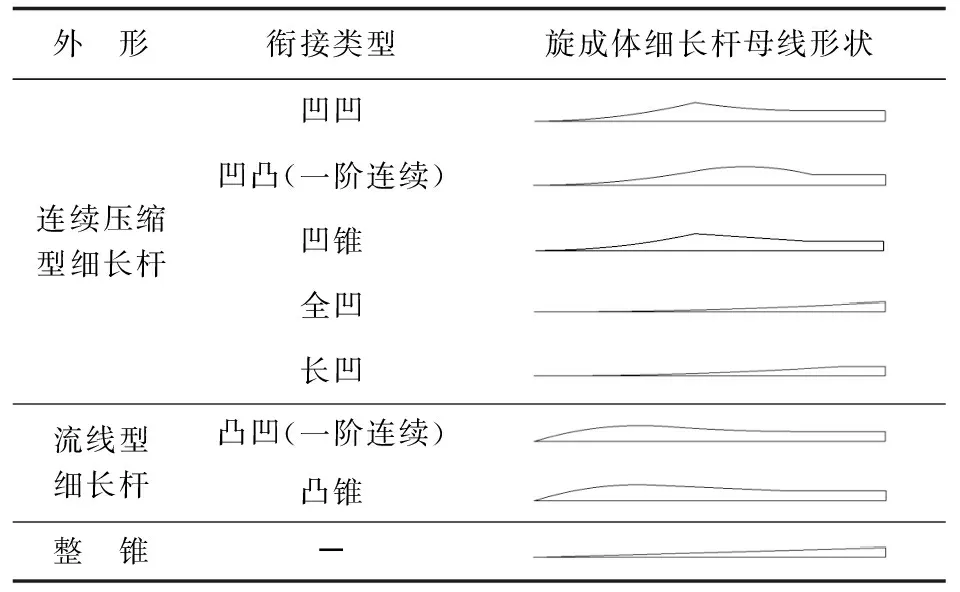
表4 不同类型细长杆形状

表5 不同类型细长杆模型的远场静压与降噪效果对比

从表5可以看出：连续压缩型细长杆和流线型细长杆均能达到较好的降噪效果，其中，凹凹面型和凹锥面型的细长杆降噪效果最为明显，其次为凸凹型、凸锥型、凹凸型细长杆和6 m锥(单级细长杆)，其他形状的细长杆降噪效果不明显。

不同形状细长杆的远场压力最大值对比如图14所示，近场压力曲线对比如图15所示。

从图14～15可以看出：①连续压缩型细长杆前端凹曲壁对来流连续压缩，凹曲壁可以看作由无数段内折的微元折壁所组成的，当超音速气流绕凹曲壁流动时，每一点都发出一道弱压缩波，所有的弱压缩波组成一个连续的等熵压缩波区，产生多道压缩波，这些压缩波在叠加成激波之前会受膨胀波系的影响而产生弯折，之后再汇聚成强激波；连续压缩型细长杆产生的激波比单级细长杆强，同时产生较强的膨胀波；机头激波被进一步减弱，近场最大压力值降低，降噪效果优于6 m锥。②凹锥面和凹凹面细长杆的降噪效果最好。③经过细长杆产生的波系压缩和膨胀之后，不同形状的细长杆产生的气流到达机头前部的压力和速度相差甚微，靠近机头位置处的压力值甚至比基本模型的压力值更高。

凹凹面型细长杆附近压力云图如图16所示，可以看出：细长杆后衔接凹面或锥面，可使气流产生较大转角，产生更强的膨胀波，且膨胀波更加靠后倾斜，即膨胀波系更加贴近机头激波，传播过程中，机头激波快速吸收膨胀波系，强膨胀波对激波的削弱作用较大，致使远场压力峰值大幅减小；此外，弯曲的细长杆激波比机头激波的倾角大，因此细长杆激波不会融入到机头激波中。以上两点是凹凹型和凹锥型细长杆降噪的主要机理。表明：除了削弱机头激波和阻碍激波合并两种手段外，在波系传播过程中，利用强膨胀波对机头激波进行削弱也是一种可行的降噪方法。

凹凸型细长杆，一阶连续面，产生的激波和膨胀波较弱，使得机头前气流密度和压力并未大幅下降，也未使细长杆激波过度弯曲，同样具有明显的降噪效果。

全凹型细长杆，没有产生明显的激波，连续压缩面较长，系列弱压缩波直接并入机头激波，其远场波形近似于N波。

长凹型细长杆，产生的激波较弱，远场波形与全凹型细长杆类似，两者的降噪效果都不明显，但它们的阻力系数相对较低。由此可知，若细长杆凹面占比过多，则不具有明显的降噪效果。

整锥型细长杆，其整锥角度较小，只产生一条弱压缩波，并且很快合并入机头激波中，远场波形呈N波形，无明显降噪效果。

连续压缩型细长杆的降噪效果比较明显，从熵增角度，连续压缩型细长杆之所以具有低噪声优势，是因为它使气体压缩过程接近于等熵压缩，总压损失小，噪声水平也越低[15]。

流线型细长杆前端为上凸面，具有较大的锥角，能产生较强激波，其降噪原理和凹凹型细长杆近似，但其气流转角没有凹凹型细长杆大，故降噪效果也没有凹凹型细长杆强。

不同形状细长杆的远场压力波形如图17所示，可以看出：连续压缩型细长杆和流线型细长杆的远场压力波形缓慢上升到最大压力值，远场压力从起始大气压值上升到最大压力值经历的空间距离增加了5～6 m，即达到压力最大值所经历的时间增加了7～9 ms，可从感官上大幅降低音爆；流线型细长杆延迟压力峰值最明显，连续压缩型细长杆的远场压力波形更接近正弦波形状；和单级锥形细长杆相比，连续压缩型细长杆和流线型细长杆在远场压力上升过程中，陡增过程占比更小，整个压力上升过程更加缓和，对降噪更有利。

8 结 论

(1) 在飞机机头部位加装合理设计的细长杆，可显著降低超音速飞机的音爆水平。

(2) 细长杆的长度能够影响其降噪效果。若长度太短，则细长杆产生的激波与机头激波快速合并，不能起到降噪作用；但细长杆的长度大于一定值后，相当于机头产生独立的激波，细长杆降噪效果不再增加。细长杆长度的最优值随着飞行高度和马赫数的变化而变化，在超音速飞行中，应采用可伸缩的细长杆，根据飞行高度和马赫数调节其长度，以达到最佳的音爆抑制效果。

(3) 选择合适锥角的细长杆，对降噪效果亦有帮助，且不会增加太多阻力。

(4) 合理设计的多级细长杆，其降噪效果优于单级细长杆。

(5) 凹凹面、凹锥面、凸凹面、凸锥面细长杆的降噪效果比较明显，在波系传播过程中，利用强膨胀波对机头激波进行削弱也是一种可行的降噪方法。

(6) 与基本模型(未加装细长杆)相比，加装了细长杆的模型可以使音爆水平大幅降低，但阻力系数略有上升。

[1] 李占科, 彭中良, 徐合良. 静音锥对超声速客机声爆水平的影响[J]. 航空工程进展, 2013, 4(3): 346-351. Li Zhanke, Peng Zhongliang, Xu Heliang. Effect of the quiet spike on sonic boom of the supersonic airline[J]. Advances in Aeronautical Science and Engineering, 2013, 4(3): 346-351.(in Chinese)

[2] Seebass R. Sonic boom minimization[J]. Journal of the Acoustical Society of America, 1971,51(49): 72.

[3] Darden C M. Sonic-boom minimization with nose-bluntness relaxation[R]. NASA TP-1348, 1979.

[4] George A R, Seebass R. Sonic boom minimization including both front and rear shocks[J]. AIAA Journal, 1971, 9(10): 2091-2903.

[5] Howe D. Improved sonic boom minimization with extendable nose spike[C]. AIAA-2005-1014, 2005.

[6] Henne P A, Howe D C, Wolz R R, et al. Supersonic aircraft with spike for controlling and reducing sonic boom: US, US6698684[P]. 2004.

[7] Thomas C L. Extrapolation of sonic boom pressure signatures by the waveform parameter method[R]. NASA TN D-6832, 1972.

[8] Taylor A D. The TRAPS sonic boom program[R]. NOAA Technical Memorandum ERL-87, 1980.

[9] Henne P. Unique applications of the method of characteristics to inlet and nozzle design problems[C]. 11th Propulsion Conference, Anaheim: 2013.

[10] Plotkin K J. PCBoom3 sonic boom prediction model-version 1.0c[R]. Wyle Research Report WR, 1996.

[11] Stusnick E. A review of recent military aviation noise programs[J]. Journal of the Acoustical Society of America, 1999, 105(2): 1276.

[12] Cowart R, Grindle T. An overview of the gulfstream/NASA quiet spike TM flight test program[C]. 46th AIAA Aerospace Sciences Meeting and Exhibit, USA: 2008.

[13] 冯晓强, 宋笔锋, 李占科. 低声爆静音锥设计方法研究[J]. 航空学报, 2013, 34(5): 1009-1017. Feng Xiaoqiang, Song Bifeng, Li Zhanke. Research of low sonic boom quiet spike design method[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1009-1017.(in Chinese)

[14] Howe D, Simmons F, Freund D. Development of the gulfstream quiet spike TM for sonic boom minimization[R]. AIAA-2008-0124, 2008.

[15] 沈沉, 周华. 细长杆降低超声速客机气动噪声的数值分析[J]. 空气动力学学报, 2012, 30(1): 39-45. Shen Chen, Zhou Hua. Numerical analysis of slender-rod-noise-reduction of supersonic passenger aircraft[J]. Acta Aerodynamica Sinica, 2012, 30(1): 39-45.(in Chinese)

(编辑：马文静)

Numerical Analysis of Slender-rod Used for Reducing Supersonic Aircraft Noise

Zhai Ronghua, Zhou Hua

(School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China)

The installation of an appropriate slender-rod on the nose of supersonic aircraft is able to reduce flight noise level. Based on Fluent quasi three-dimensional numerical simulation method, multiple slender-rod models are simulated and analyzed and compared in influence on the far-field pressure, to compare noise reduction effect of various slender-rod and summarize effective noise reduction model. Furthermore, according to the theory of aerodynamics, the solution of numerical simulation is explained, and the inner relation between the slender-rod noise reduction effect and slender-rod shape is revealed. Besides, the influence of slender-rod to the sonic boom from the aspects of the far-field pressure maximum to curve shape etc is analyzed. The results show that single-stage conical slender-rod with 6 meters length and 12.5 degrees half-cone angle is of obvious effect in noise reduction; reasonable multistage conical slender-rod significantly reduces the initial over pressure value, and delay the far-field pressure peak; concave-concave type, concave-cone type, convex-concave type and convex-cone type slender-rods greatly reduce the far-field pressure peak value and improve the shape of pressure curve and are of more significant noise reduction effect. Strong expansion wave produced by slender-rod can significantly weaken the nose shock wave in the process of shock wave propagation, thereby weakening the sonic boom.

supersonic aircraft; slender-rod; noise reduction; sonic boom; N-wave

2017-03-02；

2017-04-12

翟荣华,670012725@qq.com

1674-8190(2017)02-171-11

V211.4

A

10.16615/j.cnki.1674-8190.2017.02.009

翟荣华(1992-)，男，硕士研究生。主要研究方向：空气动力学。

周 华(1966-)，男，博士，副教授。主要研究方向：空气动力学、流体力学、计算流体力学。