考虑含界面裂纹应力集中系数的复合材料强度计算

周熠，黄争鸣

(同济大学 航空航天与力学学院，上海 200092)

考虑含界面裂纹应力集中系数的复合材料强度计算

周熠，黄争鸣

(同济大学 航空航天与力学学院，上海 200092)

弱界面复合材料受横向拉伸时，界面会在材料整体破坏前发生脱粘，材料横向拉伸强度甚至远低于纯基体的拉伸强度。为了准确地预测弱界面复合材料的偏轴强度，需要考虑和量化纤维埋入及界面脱粘对基体现场强度的影响。定义考虑界面裂纹的应力集中系数，提出一种新的方法用于预测弱界面复合材料在任意角度偏轴拉伸作用下界面脱粘对应的临界外加载荷和材料的整体强度；并对不同种类的复合材料进行算例分析。结果表明：加入新定义的应力集中系数可以明显提高预测的准确性。

复合材料；桥联模型；应力集中；界面裂纹；材料强度

0 引 言

界面性能对复合材料的横向力学性能具有重要影响[1]，由此发展出了一系列含有界面强度的强度预测经验公式[2-4]和表征复合材料界面强度的细观[5-7]和宏观[8-10]方法，例如P.B.N.Prasad等[11]从能量角度分析了界面裂纹扩展过程中Ⅰ型和Ⅱ型裂纹能量释放率的变化规律。近十年来，随着试验仪器和方法的不断改进，国内外通过宏观力学试验进行了诸多针对界面的研究。例如，考虑到层合板中90°铺层的拉伸应力比单层板横向拉伸应力更容易控制，T.Hobbiebrunken等[12]将特定铺层的宏观复合材料层合板置于SEM中进行三点弯曲试验，观察其界面的破坏过程；考虑到界面通常是在组合应力作用下破坏的，S.Ogihara等[13]提出了一种十字试件测量方法，这种试件中间包含着与外加应力呈一定角度的纤维，不同的偏轴角度可以产生不同的界面拉伸和剪切应力状态；J.Lou等[14]针对SiC/Ti-6Al-4V材料的十字形试件进行试验，以应力-应变曲线的突变点作为界面脱粘的起始点，分析了纤维体积含量对界面强度的影响；G.Qi等[15]利用骨头形的横向纤维束试件进行了横向拉伸试验来表征脱粘。

复合材料宏观力学理论认为，界面的破坏会影响组份材料之间应力的传递，从而造成复合材料整体强度降低，但却忽略了复合材料界面的破坏对基体中应力分布的影响，因此未能完整阐明弱界面复合材料的破坏机理，对强度的预测精度也不高。

桥联模型[16]是一种新兴的复合材料细观力学理论，该理论可根据组分材料的性能数据对复合材料的性能进行预测。基体失效是复合材料受横向拉伸破坏的主要原因，添加纤维后基体中产生应力集中，复合材料的横向拉伸强度甚至远低于基体的原始拉伸强度[17]，求出应力集中系数后，基体现场强度等于其原始强度除以该系数[18]。

由于制造工艺不完善和外加应力作用造成的界面缺陷是普遍存在的，完整界面应力集中系数的应用具有一定的局限性。本文从界面脱粘对应力集中系数的影响入手，分析弱界面复合材料的横向拉伸破坏，求取含有界面裂纹的复合材料受横向拉伸时基体中的精确应力场，基于细观力学桥联模型，根据纤维和基体的原始性能参数，计算弱界面复合材料的应力集中系数，将其应用于单层板偏轴拉伸强度的预测，并与实验值进行对比。

1 界面含裂纹的应力集中系数的定义

1.1 基体应力场

要得到基体的应力集中系数，首先应采用复变函数方法[19]求得受外载荷作用时，基体中的精确应力场。在理想界面的基础上，将界面缺陷转化为基体和纤维间的弧形裂纹，求取无限域基体夹单圆柱纤维受远场横向力作用的应力场。

由文献[20]给出的应力场导出如图1所示的基体中的应力场为

(1)

(2)

(3)

χ(z)=(z-aeiψ)-0.5+iλ(z-ae-iψ)-0.5-iλ

(4)

(5)

(6)

1.2 应力集中系数

1978年，A.Parvizi等[21]提出了现场强度(in-situstrength)的概念，现场强度是用来直接衡量基体是否破坏的参数，但其无法被直接测量。经典应力集中系数的定义本质上是“点应力”(孔边一点)除以“面应力”(应力施加平面的均值)，根据相似性原则，Z.M.Huang[17]指出，复合材料中基体的应力集中系数必然定义为“线平均应力”除以“体平均应力”，他采用纤维垂直方向横截面的最小特征体元为模型，以桥联理论为基础对其进行了新的定义。得到基体的现场强度后，便可以和其他组分材料性能一起，根据桥联模型预测出复合材料的总体强度。

1.3 止裂角的计算

在图1中沿x2方向施加拉力，界面沿x2轴有张开趋势，而由于基体的泊松比效应，在纤维与基体接触界面的x3轴上，必然会产生最大的界面压应力，此压应力将阻止裂纹沿界面进一步扩展。因此，界面径向相对位移由正到负变化，在止裂角处的径向相对位移为0，此处的角度即为开裂角。裂纹闭合将首先发生在界面上对应圆心角φ=ψ-γ处，由A.H.England等[22]提出的方法求出：

(7)

J1=kG0-1-2(1-k)νexp(2λψ)cosψ

(8)

J2=2(1-k)νexp(2λψ)sinψ

(9)

J3=2(1-k)νexp(2λψ)(J1cosψ-J2sinψ)/J2

(10)

止裂角方程为

(11)

1.4 积分线的选取

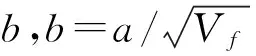
根据定义，基体中的横向拉伸应力集中系数可由式(13)确定[16-17]：

(12)

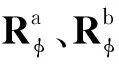
2 算例与分析

2.1 单向板偏轴拉伸强度预测

(13)

(14)

(15)

引入系数Δ用于对横向拉伸强度Y进行适度修正，Δ的取值范围一般为0.9～1.1，本文取1.0。由此可得：

(16)

(17)

(18)

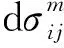
(19)

(20)

(21)

(22)

因此，界面脱粘的条件为

(23)

相应的，采用Tsai-Wu判据判断基体破坏，其形式为

(24)

(25)

2.2 偏轴拉伸强度预测算例

以E-glass/8804和Kevlar-49/epoxy两种单向复合材料为研究对象，研究考虑界面裂纹对复合材料偏轴强度预测的影响。组份材料性能如表1所示[23-26]，偏轴拉伸实验值[23,27]和预测值的对比如图3～图4所示。

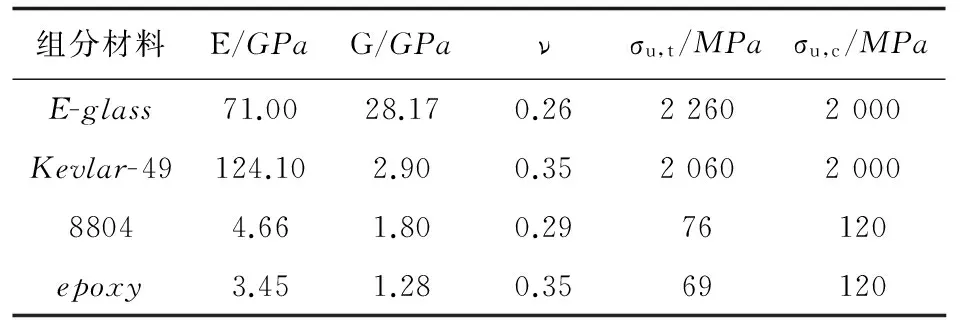
表1 复合材料组份材料性能参数

从图3～图4可以看出：未加入应力集中系数的计算结果误差最大，加入了考虑界面裂纹的应力集中系数的预测曲线与实验值最吻合，而仅加入理想界面应力集中系数对应的预测曲线介于两者之间。

3 结 论

(1) 弱界面复合材料受横向载荷的破坏顺序为：与外力方向垂直处的界面首先发生破坏，沿界面产生不稳定裂纹；裂纹角度扩展至最终发展角度，应力集中系数趋于稳定; 界面裂纹的产生影响组分材料之间应力的传递并且增大了基体中的应力集中系数；外加应力继续增大，基体由于应力集中进而发生破坏。

(2) 考虑界面脱粘对于弱界面复合材料的强度预测有明显修正，而对于具有足够界面强度的材料则影响较小。

(3) 在大角度偏轴拉伸情况下，考虑脱粘对于强度预测有明显的修正作用；在小角度偏轴拉伸情况下，剪切应力集中系数的修正作用更加明显，同时考虑两者即可对单层板偏轴拉伸强度进行准确的预测。

(4) 本文方法可以通过计算复合材料在界面部分脱粘后的应力集中系数，仅根据组份材料性能和复合材料的横向拉伸强度，就能反演出复合材料的界面强度，并以此判断出材料界面是否需要通过改性进行增强以及理想的增强幅度。

(5) 相比依赖大量实验数据的宏观力学预测方法，细观力学桥联模型理论可以仅根据组份材料的性能进行准确的强度预测，因此是预测单向复合材料力学性质的有力工具。

[1]HughesJDH.Thecarbonfibre/epoxyinterface-areview[J].CompositesScienceandTechnology, 1991, 41(1): 13-45.

[2]KattnerUR,LinJC,ChangYA.ThermodynamicassessmentandcalculationoftheTi-Alsystem[J].MetallurgicalandMaterialsTransactionsA, 1992, 23(8): 2081-2090.

[3]JanssonS,DèveHE,EvansAG.TheanisotropicmechanicalpropertiesofaTimatrixcompositereinforcedwithSiCfibers[J].Metallurgical&MaterialsTransactionsA, 1991, 22(12): 2975-2984.

[4]AghdamMM,SmithDJ,PavierMJ.Finiteelementmicromechanicalmodellingofyieldandcollapsebehaviourofmetalmatrixcomposites[J].JournaloftheMechanics&PhysicsofSolids, 2000, 48(3): 499-528.

[5]ZhouXF,WagnerHD,NuttSR.Interfacialpropertiesofpolymercompositesmeasuredbypush-outandfragmentationtests[J].CompositesPartA:AppliedScience&Manufacturing, 2001, 32(11): 1543-1551.

[6]MillerB,MuriP,RebenfeldL.Microbondmethodfordeterminationoftheshearstrengthofafiber/resininterface[J].CompositesScience&Technology, 1987, 28(1): 17-32.

[7]MandellJF,ChenJH,McgarryFJ.Amicrodebondingtestforinsituassessmentoffibre/matrixbondstrengthincompositematerials[J].InternationalJournalofAdhesion&Adhesives, 1980, 1(1): 40-44.

[8]RosenBW.ASimpleprocedureforexperimentaldeterminationofthelongitudinalshearmodulusofunidirectionalcomposites[J].JournalofCompositeMaterials, 1972, 6(3): 552-554.

[9]AdamsDF,WalrathDE.CurrentstatusoftheIosipescusheartestmethod[J].JournalofCompositeMaterials, 1987, 21(6): 494-507.

[10]MadhukarMS,DrzalLT.Fiber-matrixadhesionanditseffectoncompositemechanicalproperties: Ⅱ.longitudinal(0°)andtransverse(90°)tensileandflexurebehaviorofgraphite/epoxycomposites[J].JournalofCompositeMaterials, 1991, 25(8): 958-991.

[11]PrasadPBN,SimhaKRY.Energyreleasedduringarccrackpropagation[J].InternationalJournalofFracture, 2002, 116(1): 3-8.

[12]HobbiebrunkenT,HojoM,AdachiT,etal.EvaluationofinterfacialstrengthinCF/epoxiesusingFEMandin-situexperiments[J].CompositesPartA:AppliedScience&Manufacturing, 2006, 37(12): 2248-2256.

[13]OgiharaS,KoyanagiJ.Investigationofcombinedstressstatefailurecriterionforglassfiber/epoxyinterfacebythecruciformspecimenmethod[J].CompositesScience&Technology, 2010, 70(1): 143-150.

[14]LouJ,YangY,LuoX,etal.EffectsoffibervolumefractionontransversetensilepropertiesofSiC/Ti-6Al-4Vcomposites[J].RareMetalMaterials&Engineering, 2011, 40(4): 575-579.

[15]QiG,DuS,ZhangB,etal.Evaluationofcarbonfiber/epoxyinterfacialstrengthintransversefiberbundlecomposite:experimentandmultiscalefailuremodeling[J].CompositesScience&Technology, 2014, 105: 1-8.

[16]HuangZM.Simulationofthemechanicalpropertiesoffibrouscompositesbythebridgingmicromechanicsmodel[J].CompositesPartA:AppliedScience&Manufacturing, 2001, 32(2): 143-172.

[17]HuangZM.Micromechanicalpredictionofultimatestr-engthoftransverselyisotropicfibrouscomposites[J].InternationalJournalofSolids&Structures, 2001, 38(22/23): 4147-4172.

[18]HuangZM,LiuL.Predictingstrengthoffibrouslaminatesundertriaxialloadsonlyuponindependentlymeasuredconstituentproperties[J].InternationalJournalofMechanicalSciences, 2014, 79(1): 105-129.

[19]MuskhelishviliNI.Somebasicproblemsofthemathematicaltheoryofelasticity[M].Netherlands:Springer, 1977: 445-447.

[20]ToyaM.Acrackalongtheinterfaceofacircularinclusionembeddedinaninfinitesolid[J].JournaloftheMechanics&PhysicsofSolids, 1974, 22(5): 325-348.

[21]ParviziA,GarrettKW,BaileyJE.Constrainedcrackinginglassfibre-reinforcedepoxycrossplylaminates[J].JournalofMaterialsScience, 1978, 13(1): 195-201.

[22]EnglandAH.Acrackbetweendissimilarmedia[J].JournalofAppliedMechanics, 1965, 32(2): 400-402.

[23]StevenMayesJ,AndrewCHansen.Multicontinuumfailureanalysisofcompositestructurallaminates[J].MechanicsofCompositeMaterialsandStructures, 2001, 8(4): 249-262.

[24]RojstaczerS,CohnD,MaromG.ThermalexpansionofKevlarfibresandcomposites[J].JournalofMaterialsScienceLetters, 1985, 4(10): 1233-1236.

[25]SuppakulP,BandyopadhyayS.Theeffectofweavepatternonthemode-IinterlaminarfractureenergyofE-glass/vinylestercomposites[J].CompositesScienceandTechnology, 2002, 62(5): 709-717.

[26]HintonMJ,SodenPD.Predictingfailureincompositelaminates:thebackgroundtotheexercise[J].CompositesScience&Technology, 1998, 58(7): 1001-1010.

[27]PinderaMJ,GurdalZ,HiddeJS,etal.Mechanicalandthermalcharacterizationofunidirectionalaramid/epoxy[R].ReportCCMS-86-08,VPI-E-86-29,USA:VirginiaPolytechnicInstituteandStateUniversity, 1987.

(编辑：马文静)

Strength Prediction of Composite Materials with Consideration of the Stress Concentration Factor with Interfacial Cracks

Zhou Yi, Huang Zhengming

(School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China)

When the weak interface of composite materials subjected to the transverse tensile, the debonding of the interface will happen before the overall damage of the material, the measured transverse tensile strength of the weak interfacial bonding composite is even much smaller than the original tensile strength of the pure matrix. To predict its off-axial strength accurately, the effect of fiber embedment and interfacial debonding on in-situ strength of the matrix needs to be considered and quantified. The stress concentration factor is defined considering the existence of cracks on interfaces, and a new method is presented to predict the critical load when the interface crack occurs and the strengths of composites under off-axial tensile. Examples are given for different kinds of composite materials. The results compared with experimental data show that the accuracy of prediction can be improved obviously by considering this new stress concentration factor.

composite materials; bridging model; stress concentration; interface cracks; material strength

2017-01-12；

2017-03-14

国家自然科学基金(11272238,11472192)

周熠,976920979@qq.com

1674-8190(2017)02-119-06

TB33

A

10.16615/j.cnki.1674-8190.2017.02.001

周 熠(1991-)，女，博士研究生。主要研究方向：复合材料细观力学。

黄争鸣(1957-)，男，教授，博导。主要研究方向：复合材料细观力学。