全机有限元模型修正及验证方法研究

陈英华，陈静

(中国航空工业集团公司 中国直升机设计研究所，景德镇 333001)

全机有限元模型修正及验证方法研究

陈英华，陈静

(中国航空工业集团公司 中国直升机设计研究所，景德镇 333001)

有限元分析现已成为飞行器设计的重要工具，若要提高有限元仿真的准确性，需要对有限元模型进行必要的修正。以某型直升机全机静力试验有限元模型为研究对象，基于静力试验实测的应变值，进行变量参敏度分析和模型优化，针对全机试验测点多、模型自由度大的特点，提出适用于验证全机模型的相关性算法；基于该算法，应用某一工况下的试验结果，对全机有限元模型的部分参数进行修正，得到与试验结果符合较好的模型参数结果；应用其他工况的结果对修正后的模型进行验证，结果表明：其他工况下修正后模型的计算结果与试验值也很接近，证明了该相关性算法和全机模型修正及验证方法的可行性和有效性。

全机有限元；静力试验；模型优化；相关性算法；可行性；有效性

0 引 言

有限元分析现已成为工程结构设计的主要手段之一，借助有限元分析，可以节省大量的人力和试验成本。有限元分析结果的正确性依赖于有限元模型的质量，尤其是对于大型复杂结构，其材料属性、边界条件、连接件、接触非线性等问题的不确定性，成为制约有限元仿真精度的关键因素。通过物理试验可以得到结构较为准确的性能参数，但由于试验测点数量和试验次数等的限制，物理试验仅能得到结构的部分参数，无法预测非试验工况的结果。但可以通过试验数据来修正有限元模型的局部参数，以减少不确定性因素的影响，使有限元模型的动、静力学特性与试验结果基本一致，从而获得较为准确的有限元模型。有限元模型修正技术在结构分析、优化、损伤识别等领域具有广阔的应用前景。

根据修正的目标类型，有限元模型修正可分为动力模型修正和静力模型修正两类。动力模型修正以频率、振型等参数作为修正目标，已发展形成成熟的理论体系并进行了广泛的工程应用[1-8]；静力模型修正则以位移、应力、应变等参数作为修正目标，准确度高，但相比动力模型修正，静力试验数据无法涵盖所有自由度，并且随着约束和载荷类型的改变，一些非线性因素导致刚度矩阵随之变化，对整体模型的修正具有较大的技术难度。1996年，M.Sanayei等[9]开始对静力模型修正的算法和应用进行研究，验证了静力修正方法的可行性，但受限于非线性因素的影响，静力模型修正主要应用于土木结构的损伤识别[10-11]；2004年，田军[12]结合静力和动力参数对某型飞机机翼模型进行了修正，但所用的修正基准是细节分析的结果，缺少物理试验数据的验证，且修正目标以动力参数为主，仅将位移作为附加条件进行了修正；同年，邱春图等[13]应用模型修正技术对全机有限元模型进行修正，但修正过程中人工参与量大，模型验证工作很大程度上依赖于工程经验；2011年，刘国青等[14]基于某型飞机方向舵的静力试验，以位移、应变和内力为目标进行了模型修正，但修正的参数主要是对试验边界条件的模拟，未涉及结构本身的参数修正。

全机模型的自由度通常较大，且传力路径不唯一，由于模型的简化，无法考虑材料、接触、几何等大量非线性因素的影响，致使全机模型与真实结构之间存在较大差异，修正难度大。目前，对于全机有限元模型静力修正的结果，其精度仍难以保证，且对于大模型的有效可行的修正验证方法也鲜有报道。本文以某型直升机全机静力试验数据为基准，提出适合全机模型的相关性算法，基于该算法对该型直升机全机有限元模型进行优化，并对优化后的模型进行验证，以证明该方法的可行性和有效性。

1 相关性定义

全机模型的自由度较多，物理试验的测点数量通常较大，若仅通过一个或几个测点的数据进行分析，难以评价模型的好坏。为了判定模型的整体精度，需要对仿真结果与试验数据进行相关性分析。常用的分析方法包括标准误差、平均误差、概率误差、高斯误差以及线性回归相关性分析等，但上述算法都是对一组数据的摄动分析，不适用于全机模型的判定。基于以上算法和判定准则的要求，本文构建一种相关性分析算法，其数学表达式为

(1)

式中：xi为修正后模型的第i个测点处的计算结果；yi为试验工况的第i个测点的结果；N为测点个数。

由数学分析可知，系数r的取值范围为[0,1]，r=0表示有一组数据全为0，r=1表示两组数据完全相同。r值的大小反映了两组数据的接近程度。

2 可行方向法

全机模型修正基于Nastran优化求解器，算法采用可行方向法改进二次规划法，选择第1节定义的相关系数为目标函数。

(2)

式中：R(Z)为模型刚度矩阵中n个优化变量为Z=[z1,z2,…,zn]时的相关系数值。

随着变量矢量的变化，R(Z)值的增量为

(3)

为了使R(Z)最大或者最小，则搜索矢量方向S为

(4)

通过改变一维方向系数α*来替代n维变量的变化：

Z1=Z0+α*S1

(5)

得到R(Z)为最大值或者最小值时的α*值，结合约束方程gi，更新增量方向：

R1=R(Z0+α*S1)

(6)

(7)

再回到增量方程，反复迭代，直至得到最优解。

ΔRn(Z)<ε

(8)

3 全机模型修正

3.1 优化流程

全机模型修正分优化和验证两部分进行，具体包括试验数据对比分析及处理、变量选取及参敏度分析、模型优化、模型更新及验证等步骤，全机模型修正流程如图1所示。

3.2 工况及测点选取

某型机全机静力试验载荷包括90%两点着陆、90%偏航、100%俯冲拉起三种工况，不同工况对应考核不同机身段位的结构强度，例如两点着陆和俯冲拉起工况，中机身载荷最严重，试验应变也最大，而后机身测点的应变数据较小。考虑中机身为主承力结构，全机模型优化选择90%两点着陆工况的试验数据进行。

优化对选取的测点数量及数据质量具有一定要求，对全机静力试验中机身测点的数据进行筛选，选取主承力框梁结构上应变大的测点，最终选定15个测点，位置分别为4框内外凸缘、5框内外凸缘和腹板、主减速器前后支撑框的凸缘和腹板。

3.3 参敏度分析及优化

从有限元模型中选取待修正的变量参数，例如1D杆单元的面积、梁单元的面积、截面惯性矩、扭转惯性矩、偏置量等；2D单元的厚度、附加刚度、偏置量。将筛选后的所有测点的相关系数作为优化目标，采用Nastran优化求解器可行方向法和序列规划法，对所有变量进行参敏度分析，得到每个变量对设计目标的影响因子。

筛选灵敏度较大的变量，结构参数变量优化范围设置为±40%，优化目标为所有测点的最大主应变的相关系数最小。采用MSC.Natran软件中的优化模块进行优化，得到优化前后的变量值，如表1所示。

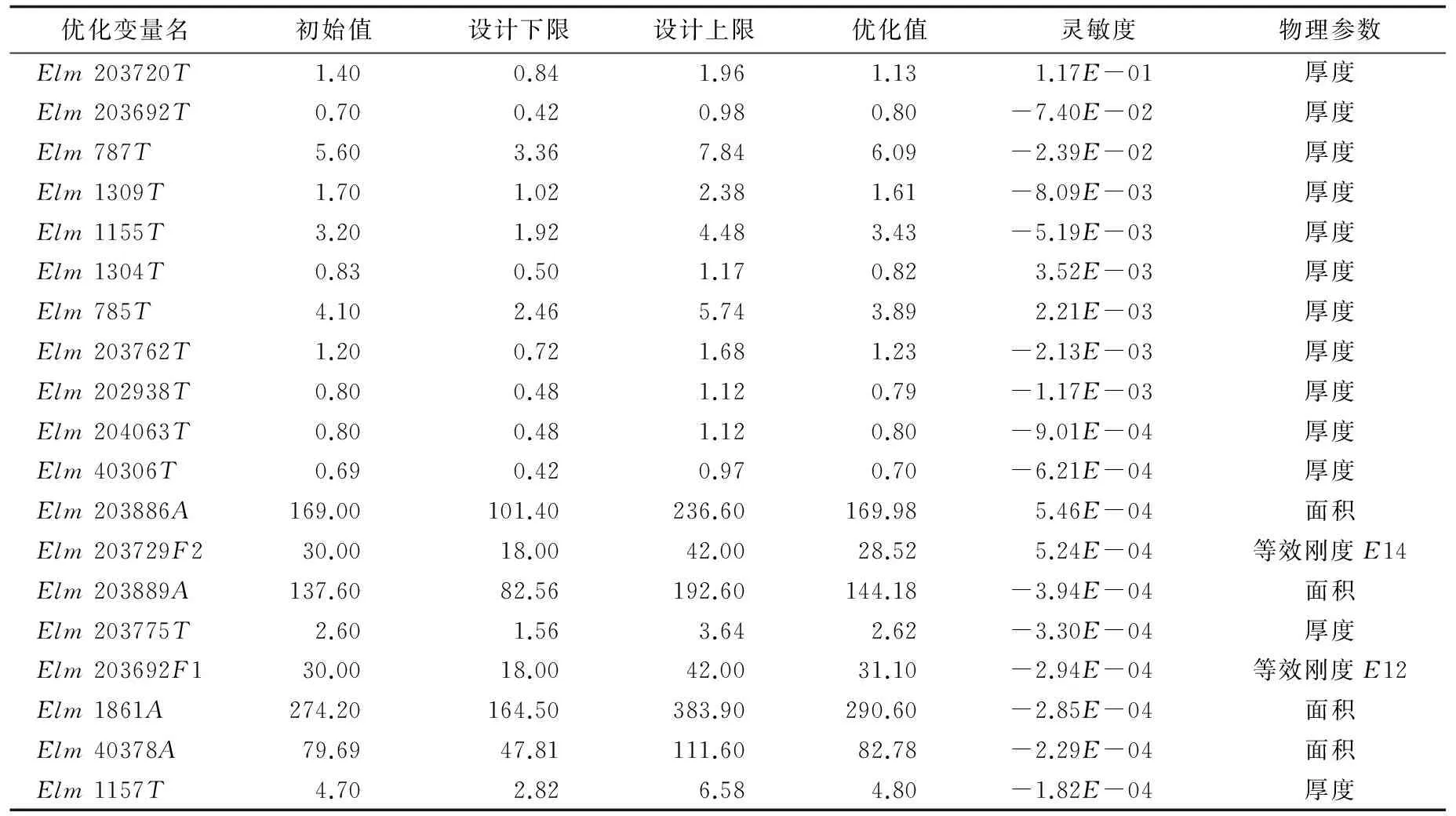
表1 变量优化前后的结果对比

90%两点着陆工况优化前后的相关系数对比如表2所示。

表2 优化前后相关系数的对比

优化前后的应变值与试验值的对比如图2所示。

3.4 模型验证

将验证工况的载荷及约束条件代入结构参数优化后的模型中进行计算，得到相应测点的仿真结果，与验证工况物理试验数据进行相关性分析，100%俯冲拉起工况和90%偏航工况验证的所有测点的相关系数如表3所示，优化前后仿真结果与试验值的对比如图3～图4所示。

从表3和图3～图4可以看出：优化后所有测点的最大主应变等相关系数值较优化前提高了约4%；优化后的值比优化前的值在整体上明显更接近试验值。表明修正后的模型在一定程度上更接近真实物理试验结构。

表3 验证工况优化前后相关系数

4 结 论

(1) 本文提出的相关性算法能够真实反映两组数据整体误差的大小，以相关系数作为优化目标，修正后测点的仿真结果与试验值在整体上明显接近，表明相关系数可以作为一个定量参数用于全机模型修正及验证。

(2) 模型的修正结果与所选测点有关，个别测点的修正结果可能出现反向偏离，因此对用于修正的物理数据及测点的选择有一定要求，应尽量选择试验数据较大的测点和主传力路径上的测点。

(3) 修正后的全机模型在本文所列工况以及其他工况下，其仿真结果均与试验值更为接近，证明了修正后全机模型的有效性。

(4) 由于全机有限元模型的传力路径不唯一，结构受载时的非线性因素较多，而结构参数的变化范围通常需要考虑物理意义，使得优化效率受到限制。如何提高优化效率、降低对测点数据的要求等尚待进一步研究。

[1] 李辉, 丁桦. 结构动力模型修正方法研究进展[J]. 力学进展, 2005, 35(2): 170-180. Li Hui, Ding Hua. Progress in model updating for structural dynamics[J]. Advances in Mechanics, 2005, 35(2): 170-180.(in Chinese)

[2] 魏来生. 结构有限元动态模型修正方法综述[J]. 振动与冲击, 1998, 17(3): 43-46. Wei Laisheng. A review on the updating methods of finite element model[J]. Journal of Vibration and Shock, 1998, 17(3): 43-46.(in Chinese)

[3] 陈德成, 魏震松, 曲广吉, 等. 有限元模型修正技术的工程应用[J]. 中国工程科学, 2001, 3(10): 59-63. Chen Decheng, Wei Zhensong, Qu Guangji, et al. Engineering application of FEM updating technology[J]. Engineering Science, 2001, 3(10): 59-63.(in Chinese)

[4] 黄东胜, 黄方林. 一种改进的动力缩聚及模型修正的方法[J]. 长沙铁道学院学报, 1996, 14(4): 72-77. Huang Dongsheng, Huang Fanglin. An improved approach to dynamic reduction and model modification[J]. Journal of Changsha Railway University, 1996, 14(4): 72-77.(in Chinese)

[5] 汪晓虹, 周传荣, 徐庆华. 结构分析模型的修正与振型扩充技术[J]. 东南大学学报: 自然科学版, 2000, 30(2): 143-147. Wang Xiaohong, Zhou Chuanrong, Xu Qinghua. Structural analytical model updating and mode shape expansion techniques[J]. Journal of Southeast University: Natural Science Edition, 2000, 30(2): 143-147.(in Chinese)

[6] Berman A, Nagy E J. Improvement of a large analytical model using test data[J]. AIAA Journal, 2015, 21(8): 1168-1173.

[7] Zhang D, Zhang L. Matrix transformation method for updating dynamic model[J]. AIAA Journal, 1992, 30(5): 1440-1443.

[8] Farhat C, Hemez F M. Updating finite element dynamic models using an element-by-element sensitivity methodology[J]. AIAA Journal, 1993, 31(9): 1702-1711.

[9] Sanayei M, Imbaro G R, Mcclain J A S，et al. Structural model updating using experimental static measurements[J]. Journal of Structural Engineering, 1997, 123(6): 792-798.

[10] Sanayei M, Saletnik M J. Parameter estimation of structures from static strain measurements.Ⅰ: formulation[J]. Journal of Structural Engineering, 1996, 122(5): 555-562.

[11] Sanayei M, Saletnik M J. Parameter estimation of structures from static strain measurements. Ⅱ: error sensitivity analysis[J]. Journal of Structural Engineering, 1996, 122(5): 563-567.

[12] 田军. 有限元模型静力-模态协同修正技术[D]. 西安: 西北工业大学, 2004. Tian Jun. Finite element model static-mode cooperative updating technique[D]. Xi’an: Northwestern Polytechnical University, 2004.(in Chinese)

[13] 邱春图, 成万植. 借助静力试验实测值修正和确认全机有限元模型[J]. 飞机设计, 2004(2): 37-41. Qiu Chuntu, Cheng Wanzhi. Corrected and validated finite element model of an aircraft according to static testing data[J]. Aircraft Design, 2004(2): 37-41.(in Chinese)

[14] 刘国青, 陈秀华, 汪海. 基于静强度试验的有限元模型修正技术研究[J]. 航空计算技术, 2011, 41(1): 101-105. Liu Guoqing, Chen Xiuhua, Wang Hai. Research on finite element model updating technique based on static strength test[J]. Aeronautical Computing Technique, 2011, 41(1): 101-105.(in Chinese)

(编辑：马文静)

The Research of Whole Aircraft FEM Modal Updating and Verification Method

Chen Yinghua, Chen Jing

(China Helicopter Research and Development Institute, Aviation Industry Corporation of China, Jingdezhen 333001, China)

FEM analysis has become an important tool for the design of aircraft. In order to improve the accuracy of FEM simulation, it is necessary to modify and update the FEM models. A FEM model of certain whole helicopter for static test is taken as the research subject. Based on strain response measured in static test experiment, a variable sensitivity analysis and model updating are performed. Because of the big numbers of measure points of the test and the huge degrees of freedom of the whole aircraft FEM, a new dependency arithmetic is presented, which is suitable for the whole model. Based on the arithmetic and combined with the results of some test case, partial parameters of the FEM model are updated to attain a better conformance with the test results. Finally, a verification with results of other load cases are performed and a conclusion is given.The conformance between test results and simulation results after the FEM model updating in other cases are also approached as predicted. The feasibility and effectiveness of the dependency arithmetic and the process of whole aircraft FEM model optimization are verified.

whole aircraft FEM; static test; model optimization; dependency arithmetic; feasibility; effectiveness

2017-01-11；

2017-03-23

陈英华,404025112@qq.com

1674-8190(2017)01-149-05

V215.5

A

10.16615/j.cnki.1674-8190.2017.02.006

陈英华(1986-)，男，博士，工程师。主要研究方向：工程力学、飞行器强度设计。

陈 静(1988-)，女，硕士，工程师。主要研究方向：工程力学、飞行器强度设计。