基于偶极势场的移动回收站空间回坞导引算法

齐贝贝, 严卫生, 高 剑



基于偶极势场的移动回收站空间回坞导引算法

齐贝贝1, 严卫生2, 高 剑2

(1. 西安航空职业技术学院 航空维修工程学院, 陕西 西安, 710089; 2. 西北工业大学 航海学院, 陕西 西安, 710072)

针对自主水下航行器(AUV)的自主回收问题, 提出了一种基于偶极势场的移动回收站空间回坞导引算法。在回收站移动的情况下, AUV动态测量应答器的位置, 从而获得AUV在对接坐标系下的坐标和姿态角, 利用建立的偶极势场计算出期望的航向角和俯仰角, 期望的横滚角设为零。在偶极势场的导引下, AUV沿回收站的中轴线进入回收站。将AUV的控制分解为纵平面和水平面两部分, 通过采用自适应非奇异终端滑模控制的方法, 分别保证航向角和俯仰角回坞控制的鲁棒性和自适应性。最后, 仿真结果证明了在回收站移动的情况下, 所设计的空间回坞导引算法是有效的。文中的工作可为移动回收站的回坞对接研究提供参考。

自主水下航行器; 移动回收站; 空间回坞导引; 偶极势场; 自适应非奇异终端滑模控制

引言

自主水下航行器(autonomous undersea vehicle, AUV)在军事和民用领域都有着巨大的应用前景。由于受制于体积与质量, AUV在执行任务时只能携带有限的能源, 为了实现长时间的水下工作, 需要在水下对AUV进行能量的补充; 同时, AUV在水下执行复杂任务时, 需要与水下对接平台进行信息交换, 包括任务信息的上传与任务使命的下载。因此, 自主回收控制技术已成为当前海洋工程领域的关键技术之一。

Lee等[1]基于视觉伺服的对接控制方法, 设计海流观测器, 使用李雅普诺夫直接法证明海流观测器的稳定性, 在线性终端导引律的设计中考虑海流的影响[2]。蒙特利海洋系统研究所针对AUV自主回收问题研究了一类水下固定式回收器[3], 在2005年和2006年分别进行了回坞和对接的海上试验。把回收对接过程分解为回坞和入坞2个阶段, 分析了2个阶段的视线导引法及跟踪控制法。Ken[4]通过使用视觉导引和横向跟踪控制的方法对AUV运动进行了研究, 忽略海流的干扰, AUV从初始位置开始运动, 采用滑模控制, 最终进入回收器。吴泽伟等[5]针对AUV回收控制问题, 采用了一种基于主-从系统同步的思想, 回收站在运动状态下实现了对AUV的自主回收。Gao等[6]基于超短基线(ultra short base line, USBL)声学定位系统, 以体坐标系下的坐标通过非线性反演技术设计反演对接控制器, 实现AUV的对接控制。Panagou等[7]首次提出了通过偶极势场进行运动控制的算法。严卫生等[8]针对AUV的水平面回坞导引问题, 采用偶极势场进行对接导引。

文中提出了基于偶极势场的移动回收站空间回坞导引算法, 针对回收站随海流移动情况下, 对回收站自主回收AUV进行研究。移动回收站的空间回坞导引, 更符合实际应用中AUV动态回收的情形。文中, AUV动态测量固定在回收站上应答器的位置, 从而计算出AUV在对接坐标系下的坐标, 利用建立的偶极势场计算出期望的航向角和俯仰角, 期望的横滚角设为零。然后采用了自适应非奇异终端滑模控制的方法, 从而保证了航向角和俯仰角跟踪控制的鲁棒性和自适应性。仿真结果证明了空间回坞导引算法是有效的。

1 问题描述

1.1 坐标系

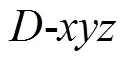
1.2 AUV动力学和运动学模型

文中, AUV在3D空间中运动, 并考虑模型参数的不确定项。AUV的动力学和运动学模型为[9]

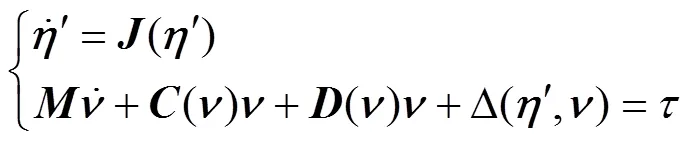
设运动中AUV的横滚角为零, 并将其运动分为纵平面和水平面的运动两部分, 不考虑2个平面运动的耦合, 可分别得到如下2个平面内的运动简化模型[9]

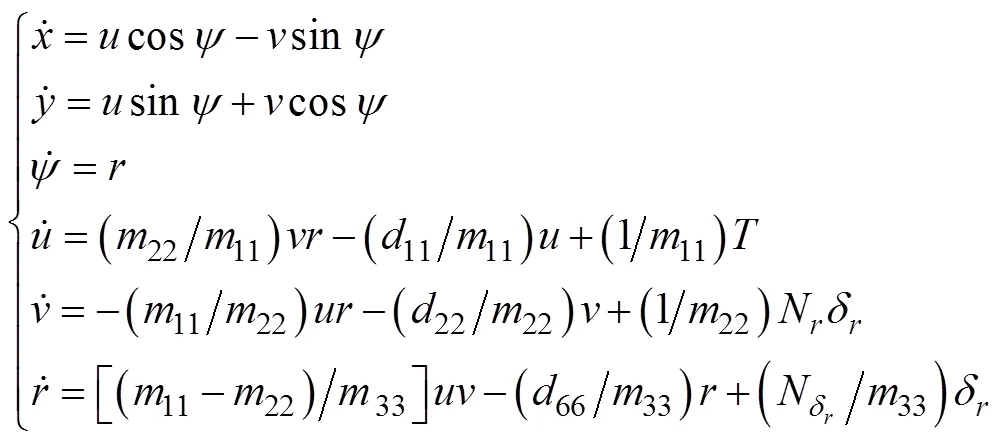
2 AUV运动参数确定

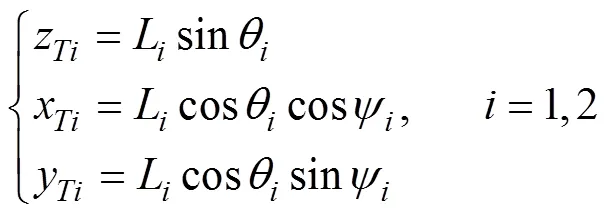
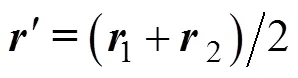
记从体坐标系到回收坐标系的坐标变换矩阵

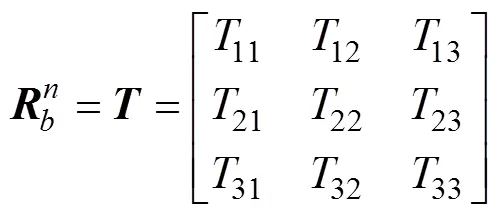
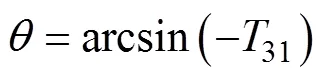
偏航角真值如表1所示。

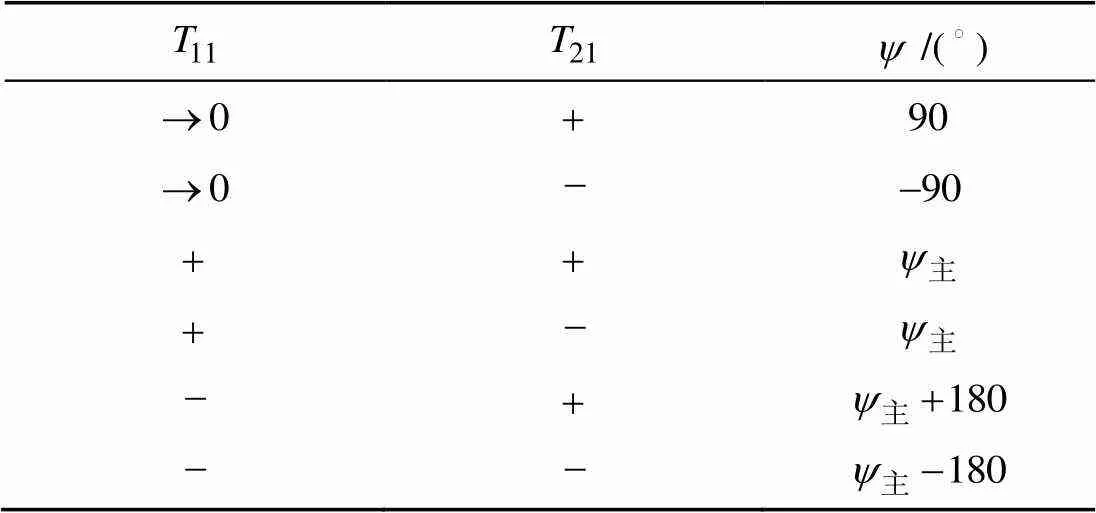
表1 偏航角真值表

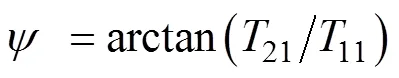
3 偶极势场

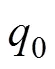
在球坐标系中, 空间中任意一点的场强[11]

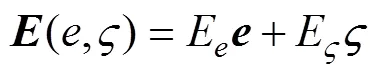
其中

如图3所示, 电偶极子的电场线垂直于电偶极矩并趋近于原点。

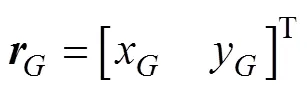
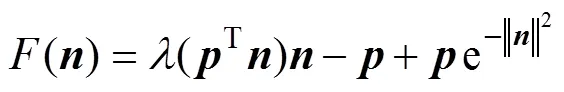
经研究得到更为简化的公式[12]

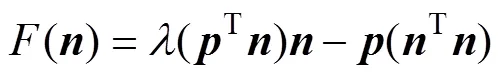
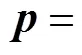
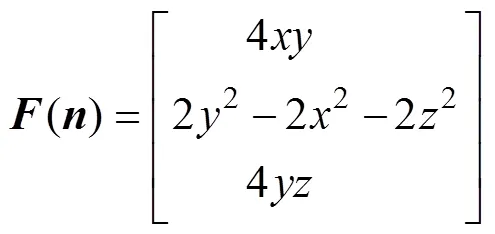
3D偶极势场在各个轴上的分量如图4所示, 假设期望的横滚角为零, 可以计算出期望的偏航角和俯仰角。

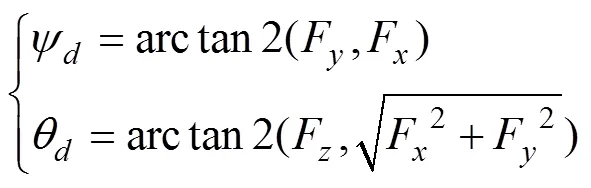
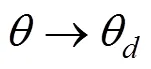
4 自适应非奇异终端滑模跟踪控制

在文中的回收控制中, 航向角和俯仰角的跟踪控制是一个非常重要的问题, 是保证AUV回坞导引效果的关键。

4.1 水平面控制

定义航向角的跟踪误差

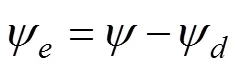
在传统的滑模变结构控制中, 有限的时间内系统状态不能渐近地收敛到零。因此采用非线性函数设计滑模面可有效改善稳态跟踪精度, 进一步采用非奇异终端滑模变结构控制的方法[8,13], 可避免普通终端滑模变结构控制设计中的奇异问题。

定义非奇异滑动面

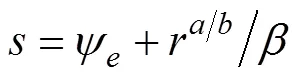
选择舵角

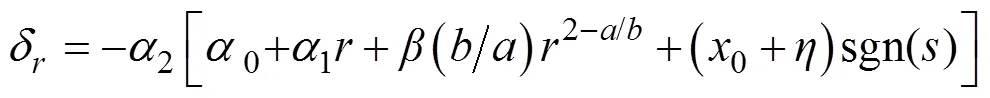
由式(17)可得

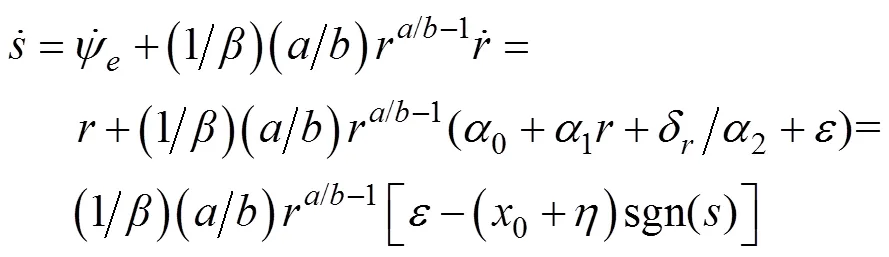
定义李雅普诺夫函数

其导数

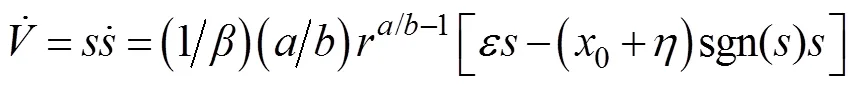
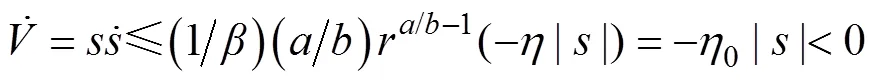
将式(18)代入式(3), 得

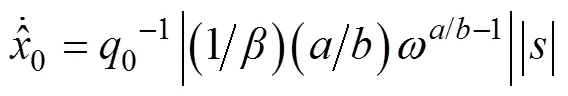
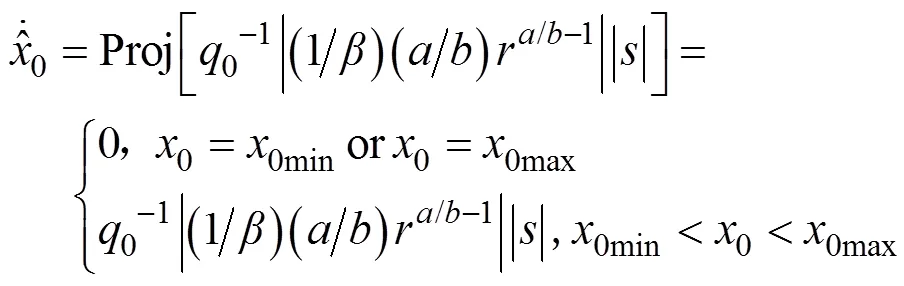
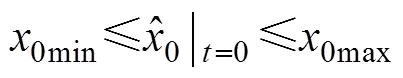
选择舵角

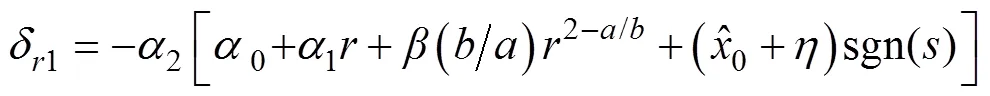
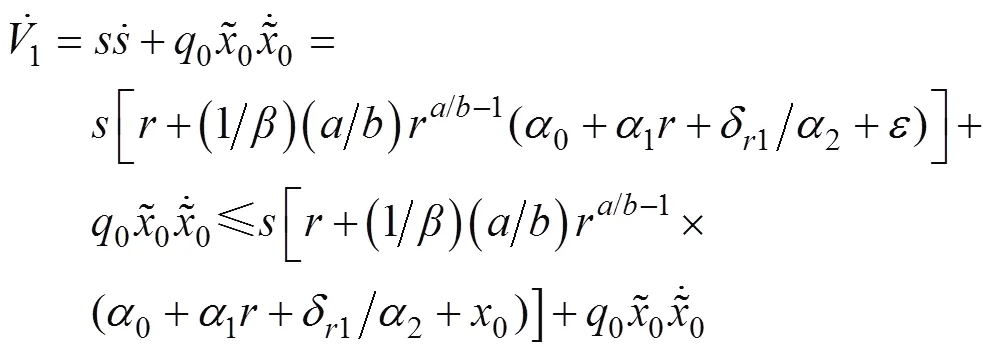
代入式(25)和式(26), 得

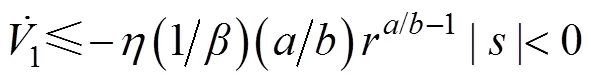
4.2 纵平面控制

与水平面的情形类似, 定义俯仰角误差

定义非奇异滑动面

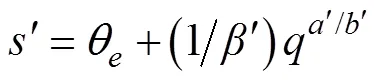
选择舵角

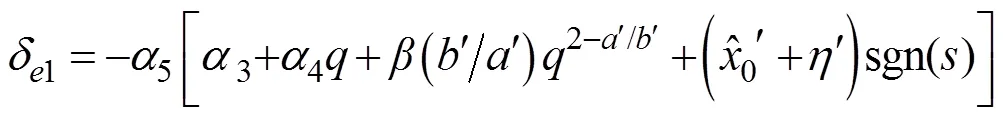
5 仿真与仿真分析

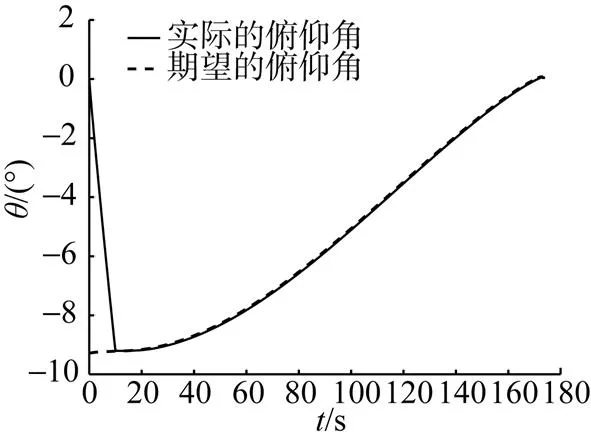
图8 AUV空间回坞俯仰角变化图

Fig. 8 Curves of pitch angle of 3D docking versus time for an AUV

从图6中可以看到, 在回收站发生移动的情况下, 采用自适应非奇异终端滑模控制, AUV能够以较光滑的轨迹、在较短的时间内进入回收站。AUV航行过程中偏航角和俯仰角的变化分别如图7和图8所示, 实际偏航角和指令偏航角的误差、实际俯仰角和指令俯仰角的误差都非常小, 可以完成回坞任务。AUV航行过程中垂直舵角和水平舵角的变化如图9和10所示, 从图中可以看出, 刚开始时为了调整初始航向, 舵机打满舵; 当跟踪上期望的姿态角之后, 舵角始终保持较小值。加入随机噪声对回坞轨迹和航向角的变化影响很小, 说明了导引算法的有效性。

6 结束语

文中针对移动回收站的AUV空间动态回收问题, 提出了一种基于偶极势场的空间回坞导引算法。在回收站移动的情况下, 首先AUV动态地测量回收站上应答器的位置, 从而计算出AUV在对接系下的坐标, 利用建立的偶极势场计算出期望的航向角和俯仰角。然后将对AUV的控制分解为纵平面和水平面两部分, 忽略2个部分运动的耦合。自适应非奇异终端滑模控制作为控制方法, 分别保证了航向角和俯仰角跟踪导引控制的鲁棒性和自适应性。最终仿真结果证明了该空间回坞导引算法是有效的。仿真中移动回收站的移动条件比较理想, 综合考虑海流和海浪的影响将是下一步研究的方向。

[1] Lee P M, Jeon B H, Kim S M. Visual Servoing for Un- derwater Docking of an Autonomous Underwater Vehicle with One Camera[C]//Proceedings of the MTS/IEEE Oc- eans Conference. San Diego, California, USA: MTS/ IEEE, 2003: 677-682.

[2] Park J Y, Jun B H, Lee P M, et al. Modified Linear Te- rminal Guidance for Docking and a Time-varying Ocean Current Observer[C]//Underwater Technology(UT), 2011 IEEE Symposium on and 2011 Workshop on Scientific Use of Submarine Cables and Related Technologies(SSC). Tokyo, Japan: IEEE, 2011: 1-6.

[3] McEwen R S, Hobson B W, McBride L, et al. Docking Control System for a 54-cm-Diameter(21-in) AUV[J]. IEEE Journal of Oceanic Engineering, 2008, 33(4): 550- 562.

[4] KenT,EdgarA,Pierre-PhilippeJ. A robust Fuzzy Auto- nomous Underwater Vehicle(AUV) Docking Approach for Unknown Current Disturbances[J]. IEEE Journal of Ocea- nic Engineering, 2012, 37(2): 143-155.

[5] 吴泽伟, 吴晓锋. 基于有限时间系统同步的自治水下航行器回收控制[J]. 自动化学报, 2013, 39(12): 2164- 2169. Wu Ze-wei, Wu Xiao-feng. Recovery Control for Auton- omous Underwater Vehicle based on Finite-time Synchr- onization of Systems[J]. Acta Automatica Sinica, 2013, 39(12): 2164-2169.

[6] Gao J, Liu C X, Wang Y X. Backstepping Adaptive Do- cking Control for a Full-actuated Autonomous Underwater Vehicle with Onboard USBL System[C]//Oceans’14 MTS/ IEEE St. John’s, St. John’s, Newfoundland, Canada: MTS/ IEEE, 2014: 1-6.

[7] Panagou D, Tanner H G, Kyriakopoulos K J. Dipole-like Fields for Stabilization of Systems with Pfaffian Constra- ints[C]//IEEE International Conference on Robotics and Automation(ICRA). Anchorage, Alaska, USA: IEEE, 2010: 4499-4504.

[8] 严卫生, 齐贝贝, 高剑, 等. 基于偶极势场的自主水下航行器回坞导引算法[J]. 系统工程与电子技术, 2016, 38(4): 902-908.Yan Wei-sheng, Qi Bei-bei, Gao Jian, et al. Dipolar Field based Homing Guidance Algorithm for an Autonomous Underwater Vehicle[J]. Systems Engineering and Electr- onics, 2016, 38(4): 902-908.

[9] Fossen T I. Guidance and Control of Ocean Vehicles[M]. Hoboken, NJ, USA: John Wiley & Sons Inc, 1994.

[10] 秦永元. 惯性导航[M]. 北京: 科学出版社, 2014.

[11] 梁灿彬, 秦光戎, 梁竹健. 电磁学[M]. 北京: 高等教育出版社, 2004.

[12] Panagou D, Kyriakopoulos K J. Dynamic Positioning for an Underactuated Marine Vehicle Using Hybrid Control[J]. International Journal of Control, 2014, 87(2): 264-280.

[13] Feng Y , Yu X H, Man Z H. Non-singular Terminal Slid- ing Mode Control of Rigid Manipulators[J]. Automatica, 2002, 38(12): 2159-2167.

[14] Loannou P, Fidan B. Adaptive Control Tutorial[M]. Phil- adelphia: Society for Industrial and Applied Mathematics, 2006.

(责任编辑: 杨力军)

3D Docking Guidance Algorithm Based on Dipole Field for a Moving Dock Station

QI Bei-bei1, YAN Wei-sheng2, GAO Jian2

(1.College of Aircraft Maintenance Engineering, Xi’an Aeronautical Polytechnic Institute, Xi’an 710089, China; 2. Colle- ge of Marine Engineering, Northwestern Polytechnical University, Xi’an 710072, China)

To solve the autonomous docking problem of an autonomous undersea vehicle(AUV), a three-dimensional (3D) docking guidance algorithm based on dipole field is presented for a moving dock station. The position of the transponder is dynamically measured under moving condition of the dock station, and the coordinate and attitude angle of the AUV in docking coordinate system are obtained. The expected heading angle and pitch angle are calculated by using the established dipole field, and the expected roll angle is set to zero. Under the guidance of dipole field, the AUV enters the dock station along the central axis. The control of the AUV is decomposed into two parts in respective longitudinal plane and horizontal plane. By adopting adaptive nonsingular terminal sliding mode control, the robustness and adaptability of controlling heading angle and pitch angle in docking are guaranteed. Simulation shows that the 3D docking guidance algorithm is effective for the moving dock station. This work may provide a reference for the research on docking of moving dock station.

autonomous undersea vehicle(AUV); moving dock station; three-dimensional docking guidance; dipole field; adaptive nonsingular terminal sliding mode control

齐贝贝, 严卫生, 高剑.基于偶极势场的移动回收站空间回坞导引算法[J]. 水下无人系统学报, 2018, 26(3): 221-227.

TJ630; TP242.3; TP273

A

2096-3920(2018)03-0221-07

10.11993/j.issn.2096-3920.2018.03.006

2018-01-28;

2018-03-28.

齐贝贝(1990-), 女, 硕士, 主要研究方向为水下航行器导航与控制.