多动能拦截器协同制导规律的研究及仿真

王 飞,周爱美,王宇霄

(浙江广厦建设职业技术大学,浙江 东阳 322100)

0 引言

多拦截器协同作战环境异常复杂,对制导规律提出了更高的要求。它要求拦截器不仅能拦截目标,还应能配合其它拦截器,使拦截作战效能最大化。到目前为止,国内外对多导弹协同作战环境中制导规律的研究,仍局限于固有的模式,即把导弹间的战术级协同和单枚导弹的制导规律分开来研究。而对多导弹的协同制导规律的研究仍处于初步探索阶段,目前尚未有相关研究报告公开发表。本文以多拦截器协同作战为研究背景,将现代博弈理论与传统导引规律相结合,主要开展多拦截器拦截弹道导弹目标时的协同制导规律的研究。

1 模型研究

1.1 动能拦截器作战过程描述

典型的动能拦截器拦截战术弹道导弹(tactical ballistic missiles,TBM)主要采用直接碰撞动能杀伤方式。即在地面制导控制系统导引下,拦截弹先到达较高的预定空域,并具有很大的速度；接着,位于拦截弹前端的动能拦截器分离出来,由其头部红外成像导引头实现对目标的精确探测；最后,动能拦截器利用姿控、轨控发动机的直接侧向力实现快速变轨和姿态调整,利用自身高速运动的巨大动能直接碰撞摧毁目标。图1为动能拦截器制导控制仿真结构图。

图1 动能拦截器制导控制仿真结构图

1.2 拦截问题的对策模型描述

在二维有界矩形环境(追踪区域)中,假设有两枚拦截器同时拦截目标,垂直平面内交会情况如图2所示。拦截器1 和拦截器2 分别记为M1和M2,目标记为T,拦截器的速度分别为和,加速度分别为和,目标的速度为,加速度为,拦截器到目标的距离分别为和。

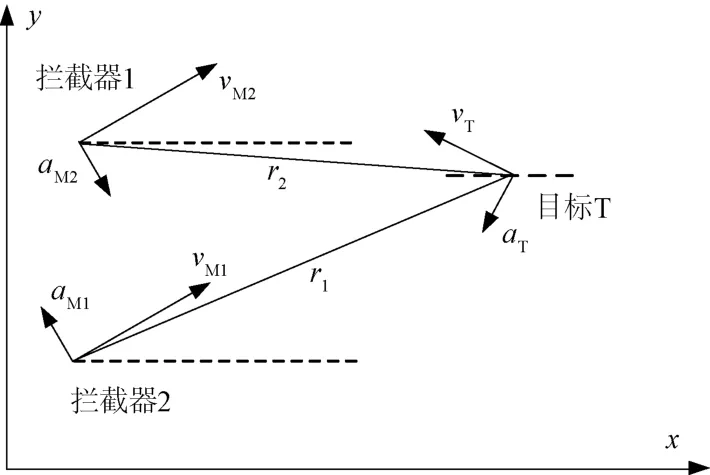
图2 垂直平面内交会示意图

为了方便研究,对空间和时间进行离散化。时间离散化后用1,2,…表示,并假定环境以及相互位置信息对于拦截器和目标双方均是已知的,在每个时刻由于目标机动,拦截器也随着同时机动,且只能执行一次机动。

由于拦截器的设计限制,加速度方向只能从垂直当前速度的正负方向中选取,而且大小受限。即对于容许控制集,控制变量u 应满足

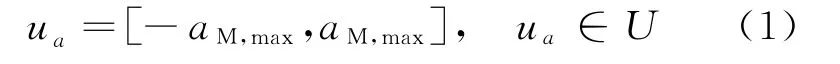
式中:为动能拦截器的最大加速度。目标被第枚拦截器拦截时,应满足

式中:r ()为时刻第枚拦截器和目标之间的距离；为脱靶量。即拦截器与目标距离不大于指标要求的脱靶量。

1.3 协同制导中博弈模型描述

将拦截器-目标双方的动态拦截模型按时间离散化,转化成具有两个局中人(拦截器及目标)的离散动态对策问题,每个时刻的动作选择问题转化为矩阵对策的形式求解。因此,协同制导中博弈模型可以用3部分来描述:参与者集合,动作集合,应用性能评估函数。

参与者集合,即拦截问题中的所有拦截器以及目标。将两枚拦截器看作是一个合作的团队,并假定它们具有集体理性,即在对抗中各拦截器并不是根据个体利益最大化进行行为决策,而是追求集体利益最大化,可以看作是一个参与者。

动作集合,是参与者在时刻所能完成的容许控制集。

应用性能评估函数作为参与者的代价函数,用于计算局势的评估值并以此作为参与者的支付值。应用性能评估主要包括拦截器与目标距离的评估和拦截器对目标的包围态势的评估两部分。

拦截器的目的是形成一定的决策,成功拦截目标,使其支付值最大。目标的目的是尽量逃离拦截器。两个局中人的目的互相冲突,构成一个两人的零和矩阵对策。

1.4 代价函数

在时刻拦截器-目标双方各自采取了某种制导策略后,就形成一个局势。为了衡量所形成局势的好坏,引入应用性能评估函数评估当前全局环境对拦截器-目标双方的目的完成的贡献程度。拦截器的目的是尽量拦截到目标,目标的目的是尽量逃脱拦截器的拦截,可见拦截器与目标的支付值是冲突的,完全相反的。因此拦截器与目标之间的博弈可以看作是一种零和博弈,即()()0,其中(),()分别为拦截器与目标的代价函数。

为了描述某个局势对支付值的贡献大小,要考虑两个因素:距离影响因子r 和有效包围因子r。

则定义拦截器的代价函数

式中:k 和k为代价函数系数,且k +k=1；k=,其中为初始代价函数系数,为衰减因子。

在刚开始拦截的时候可以将k设得较大,而k 较小,使拦截器更重视对目标的包围。随着时间的变化,有效包围因子r的重要性越来越小,而距离影响因子r 的重要性相应提高。在拦截器对目标形成一定包围态势后,主要以与目标之间的距离作为策略选择的依据。

距离影响因子r 是指拦截器在距离上对支付值的贡献程度,显然距离越近,则离目的的完成越近。因此,定义距离影响因子

式中:为拦截器个数；为初始时刻拦截器与目标之间的距离；r ()为时刻第枚拦截器与目标之间的距离。距离影响因子使拦截器趋向于选择使其与目标之间距离缩短的策略,体现的是拦截器的个体行为。

有效包围因子r是用来衡量拦截器在方位上对目标的协同拦截程度。拦截器对目标构成某种包围态势时,可将其近似等效为以目标T 为中心的一段圆弧。第枚拦截器阻挡的方向的集合,称为该拦截器的可攻击区域,记为θ。第枚拦截器的可攻击区域如图3所示。

图3 第i枚拦截器的可攻击区域示意图

θ是以目标为圆心,以第枚拦截器为中点的一段弧长为2d 的范围,为简单起见,设θ=π/2。因此,定义有效包围因子

式中:为常数；sum{·}为所有拦截器可攻击区域范围的并集的大小。有效包围系数鼓励拦截器之间进行合作,包围目标,体现了拦截器之间的协作行为。

同理,因为拦截器与目标的支付值相互冲突,构成的是零和博弈,因此目标的代价函数()()。

2 协同制导规律及其解法

2.1 协同制导规律算法求解

在时刻,对某种局势,根据1.4节的代价函数(性能评估函数)公式可以计算得到拦截器的支付值。因此可以根据时刻对抗双方各种可能的走步策略构造拦截器支付矩阵

式中:h ()表示时刻目标采取第种机动策略,拦截器选择第种机动策略时拦截器的支付函数。

在拦截过程中,拦截器和目标知道双方的机动能力,但不知道对方会具体选择哪个机动策略,因此,双方都以避开较大不利为决策依据。这种情况下,可运用“排除法”求出无鞍点矩阵对策的纯策略解,这只是对策的满意纯策略解,但可直接指导策略的选取。“排除法”的具体求解步骤为:

a)写出拦截器的支付矩阵(),每行代表拦截器的一个策略,而每列代表目标的一个策略；

b)在矩阵()中寻找最小的元素,将该元素所在的行划去,然后在剩下的各行中寻找最小的元素,再将该元素所在的行划去,依次进行,直到剩下唯一的一行,即为拦截器将选择的策略；

c)同理,在支付矩阵()中寻找最大的元素,将该元素所在的列划去,然后在剩下的各列中寻找最大的元素,再将该元素所在的列划去,依次进行,直到剩下唯一的一列,即为目标将选择的最优策略；

d)如果最小(最大)的元素,在若干行(列)中同时出现,则比较这几行(列)中次小(大)的元素,若还相等,则比较再次之的元素,直到能比出大小为止,再按步骤b)和步骤c)的标记方法执行；

e)最后必有一个元素没有被划去,则此元素的值便是对策的值,此元素对应的局中人双方的纯策略便是对策的解；

f)对于某些特殊的支付矩阵,通过上述步骤可能找不到最小(大)值,就意味着对于局中人双方来说,按照“排除法”的原则,每个纯策略的不利程度是相同的,即取任意一行(列)都是可行的。

根据前面的分析,可以得到对策论框架下多枚拦截器攻击问题的实时策略选择算法。其形式化描述为:

a)初始化处理,给定各枚拦截器及目标的初始位置；

b)结束条件判断,根据前面的拦截定义判断是否拦截到目标,如果是,则算法终止,否则继续下一步；

c)策略生成,根据-1时刻拦截器和目标的位置,生成时刻双方的可行机动策略；

d)策略评价,根据步骤c)生成的各种机动策略,分别计算相应的支付值,得到拦截器的支付矩阵；

e)策略选择,用“排除法”求解支付矩阵,得到双方在时刻的最优机动策略；

f)策略执行,执行该机动策略,并返回步骤b)。

2.2 拦截器飞行弹道的平滑处理

由于将时间进行了离散化,使得直接得到的拦截器飞行轨迹是由一系列线段首尾相连而成的。考虑到拦截器的转弯半径,这样的弹道并不满足拦截器的飞行条件,因此还需要对弹道进行进一步的平滑。

不失一般性,设根据制导规律得到的拦截器弹道的转弯点由3点构成。ω,ω,ω分别为3点的位置向量,并定义相邻两点的单位向量d ,d 的公式为

式中:‖·‖表示范数运算。

则两向量d ,d 间的夹角

在的角平分线上以拦截器的最小转弯半径为半径作圆,圆与ω-ω和ω-ω相切,有两个交点,设靠近ω的交点为。令

根据几何关系可求得点的位置矢量

用()表示参数化后的点矢量

显然(0)=ω,(1)=。这样,根据需要选择不同的,就能够得到不同的平滑结果。拦截器弹道平滑示意图如图4所示。

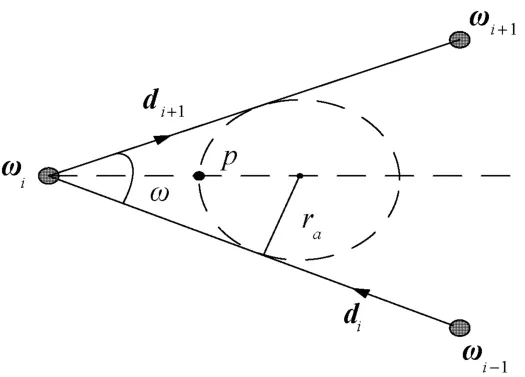
图4 拦截器弹道平滑示意图

3 仿真结果及分析

3.1 顺轨拦截

(1)仿真想定1

假设有两枚拦截器拦截弹道导弹目标,拦截器和目标在水平面内同向运动,且只在水平面内机动,拦截器机动飞行到目标轨道前,实现顺轨拦截。目标初始位置为(0,10 000)(单位为m,下同),沿着轴作匀速运动,速度为1 000 m/s。拦截器1和拦截器2由同一载体发射,初始位置为(0,0),速度均为1 500 m/s。仿真时间固定步长Δ=0.1 s。分别对拦截器在不同衰减因子、不同初始代价函数系数情况下的顺轨拦截轨迹进行仿真,结果如图5和图6所示。

图5 想定1不同衰减因子的拦截器顺轨拦截轨迹(k0=0.6)

图6 想定1不同初始代价函数系数的拦截器顺轨拦截轨迹(u=0.7)

从图5和图6的仿真结果来看,在不同衰减因子、不同初始代价函数系数情况下,拦截器顺轨拦截轨迹明显不同。衰减因子和初始代价函数系数共同决定了拦截器对目标的包围程度,其取值越大,拦截器对目标的包围程度就完成得越好,而且弹道相对平滑,同时拦截时间随之增大。

(2)仿真想定2

假设有两枚拦截器拦截弹道导弹目标,拦截器和目标在水平面内同向运动,且只在水平面内机动,拦截器机动飞行到目标轨道前,实现顺轨拦截。目标初始位置为(0,10 000),沿着轴作匀速运动,速度为1 000 m/s。拦截器1和拦截器2由不同载体发射,初始位置分别为(0,1 000)和(0,-1 000),速度均为1 500 m/s。仿真时间固定步长Δ=0.1 s。对拦截器在不同衰减因子、相同初始代价函数系数情况下的顺轨拦截轨迹进行仿真,结果如图7所示。

图7 想定2不同衰减因子下拦截器的顺轨拦截轨迹(k0=0.6)

仿真想定2的仿真环境与仿真想定1的区别在于,两枚拦截器的发射初始位置不同,但是从图7所示的仿真结果来看,只要两枚拦截器能够同时发射,依然可以进行协同制导。在相同初始代价函数系数情况下,衰减因子越大,其包围态势越明显。

3.2 逆轨拦截

(1)仿真想定1

假设有两枚拦截器拦截弹道导弹目标,拦截器和目标在水平面内反向运动,且只在水平面内机动,拦截器机动飞行到目标轨道前,实现逆轨拦截。目标初始位置为(0,10 000),沿着轴作匀速运动,速度为1 000 m/s。拦截器1和拦截器2由同一载体发射,初始位置为(0,0),速度均为800 m/s。仿真时间固定步长Δ=0.1 s。对拦截器在不同衰减因子、相同初始代价函数系数情况下的逆轨拦截轨迹进行仿真,结果如图8所示。

图8 想定1不同衰减因子下拦截器的逆轨拦截轨迹(k0=0.6)

从仿真结果来看,在逆轨拦截的情况下,也可以进行协同制导。在相同初始支付函数系数、不同衰减因子情况下,衰减因子越小,其包围态势越明显。这一结论和顺轨拦截正好相反。

(2)仿真想定2

假设有两枚拦截器拦截弹道导弹目标,拦截器和目标在水平面内反向运动,且只在水平面内机动,拦截器机动飞行到目标轨道前,实现逆轨拦截。目标初始位置为(0,10 000),沿着轴作匀速运动,速度为1 000 m/s。拦截器1和拦截器2由不同载体发射,初始位置分别为(0,1 000)和(0,-1 000),速度均为800 m/s。仿真时间固定步长Δ=0.1 s。对拦截器在不同衰减因子、相同初始代价函数系数情况下的逆轨拦截轨迹进行仿真,结果如图9所示。

图9 想定2不同衰减因子下的拦截器逆轨拦截轨迹(k0=0.6)

仿真想定2的仿真环境与仿真想定1的区别在于,两枚拦截器的发射初始位置不同,但是从图9所示的仿真结果来看,只要两枚拦截器能够同时发射,依然可以进行协同制导。在相同初始代价函数系数情况下,衰减因子越小,其包围态势越明显。

从图5～图9的仿真结果来看,拦截器在飞行的初始阶段更重视对目标的包围,随着时间的变化,逐渐转为以与目标之间的距离作为制导策略选择的主要依据。这是因为随着时间的变化,有效包围系数越来越小,而距离影响系数则越来越大。

另外协同制导规律是在协同反导作战体系作战条件的基础上进行研究的,因为各枚拦截器需要指挥控制中心提供彼此的相互位置信息,衰减因子和初始代价函数系数的取值应考虑拦截器之间通信距离的上限。

4 结论

本文以多拦截器协同反导作战为研究背景,将现代博弈理论与传统导引规律相结合,主要研究多枚拦截器拦截弹道导弹目标的协同制导规律。该制导规律有效结合了对策论的思想,在协同制导领域进行了积极探索,但是它只适用于拦截器拦截匀速目标或机动能力较小的目标的情况,且多以拦截器同时到达目标位置为前提,若拦截器不能同时到达目标位置,对目标的包围也就没有意义了。因此,下一步要研究的问题是如何将本文的协同制导规律与攻击时间控制制导规律有效结合。