基于互质多载频MIMO雷达的DOA估计
刘爱华,杨 娜,占 凯,黄 飞,周 焯
(上海无线设备研究所,上海 201109)
0 引言
多输入多输出(multiple input multiple output,MIMO)雷达发射正交波形,在空间实现宽波束覆盖,在接收端采用匹配滤波实现正交波形分离,形成虚拟通道,提升系统的自由度。MIMO 雷达通过对虚拟接收通道的回波数据进行波束形成处理,可进行空间同时多波束接收,实现大空域多目标测角。利用阵列波达方向(direction of arrival,DOA)估计方法,可实现主瓣内目标角度超分辨处理。相比于阵元数相同的相控阵雷达,MIMO 阵列雷达具有更多的接收通道、更大的有效孔径、更高的测向精度和角度分辨力,因而在波束形成与DOA 估计领域受到广泛的关注。
经典的阵列DOA 估计方法有两大类:一类为传统的子空间方法,典型的为多信号分类(multiple signal classification,MUSIC)算法及其变体,该类算法需要信号有多次快拍,不能处理单次快拍数据;另外一类算法为压缩感知方法,该类算法可以处理单次快拍数据,其中基于网格的压缩感知方法存在网格失配问题,而无网格的压缩感知方法可以避免网格失配问题。
另外,可以通过互质阵列提升阵列雷达的孔径和阵列自由度。互质阵列本质上是一种非均匀直线阵列,可将其分解成两个稀疏均匀直线阵列。稀疏阵列的阵元间距大于工作频率的半波长,且两个稀疏均匀直线阵列的归一化阵元间距互为质数。为了避免稀疏带来的角度模糊问题,一般利用互质空间的解模糊特点实现目标角度估计的解模糊。利用互质阵列,在使用个阵元的情况下,最多能获得个自由度。对于一个由个阵元组成的均匀直线阵列,其阵列自由度为1。相比均匀直线阵列,互质阵列的自由度得到了较大的提升。另外由于其阵元间距大于半波长,其阵列孔径更大,角度分辨力更高。
为了进一步提升MIMO 雷达阵列的等效孔径和自由度,可以在MIMO 雷达中采用互质多载频模式,通过将MIMO 等效阵列的阵元间距设置为大于半波长,提升等效阵列的等效孔径。通过采用互质载频,即发射的多个载频归一化后两两互质,实现角度解模糊处理,同时在互质空间形成具有更多等效阵元的虚拟阵列,进一步提升MIMO 雷达的自由度。
本文给出了互质多载频MIMO 雷达阵列的信号模型与等效阵列DOA 估计方法,并仿真分析了信噪比对互质空间DOA 估计精度的影响。
1 互质多载频MIMO 信号模型
1.1 互质多载频MIMO 等效虚拟阵列原理
考虑一个简单的MIMO 雷达模型,发射和接收阵列都为均匀直线阵列,两个阵列都位于轴上。发射阵列由个发射阵元组成,阵元之间的间距为,接收阵列由个接收阵元组成,阵元之间的间距为,其中=。发射阵列中每个辐射单元都能同时发射个互质载频f =M f(=1,2,…,),其中M 为两两互质的整数,为参考频率。
假设空域中存在个远场非相干目标,其对应的波达方向角为=[θ],其中矩阵元素θ∈[0,π)(1,2,…,)为目标回波与轴正向的逆时针方向夹角,MIMO 发射和接收阵列模型示意如图1所示。
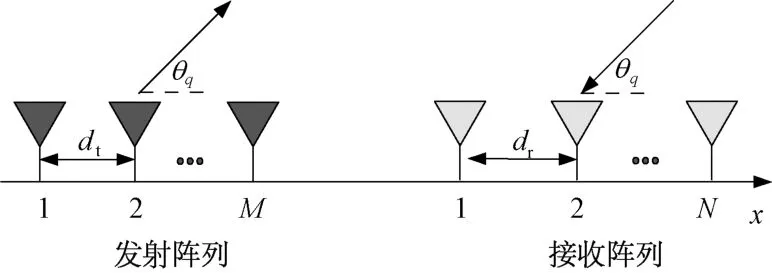
图1 MIMO 发射和接收阵列模型示意
在MIMO 的发射阵列端,第个阵元辐射信号s ()(1,2,…,)被同时调制到个互质载频上,然后通过第个阵元辐射到空间;在接收阵列端,第个接收阵元首先通过混频滤波,实现个载频回波的分离,分离后的回波继续与个正交参考信号进行匹配处理,从而实现个发射正交回波的分离。接收端的每个接收阵元通过混频滤波和匹配处理,都可以获得个等效接收通道,即,接收端共计可以获得个等效接收通道。传统的相控阵采用个接收阵元,其自由度为1。采用多载频MIMO 体制,系统的自由度可以增加到,极大地提高了雷达的阵列自由度。
通过以上分析可知,对于载频f ,其接收信号模型为
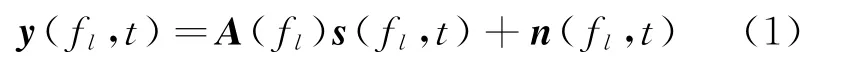
式中:(f )=[(f ,θ)]是载频为f 的MIMO等效阵列流型矩阵,其中(f,θ)=(f,θ)⊗(f,θ)是载频为f的MIMO 等效接收阵列在θ方向上的阵列导向矢量,(f ,θ)和(f ,θ)分别是发射阵列和接收阵列在θ方向上的阵列导向矢量,运算符⊗表示Kronecker 乘积;(f ,)[s (f,)]是个远场非相干目标在载频为f 的信号照射下的反射系数矩阵,其中s (f ,)为第个目标的反射系数,T 表示矩阵或者向量的转置;(f ,)是方差为的高斯白噪声矩阵。
采用参考频率对载频f 进行归一化处理,可以获得载频f 的等效接收阵列的阵元位置集合
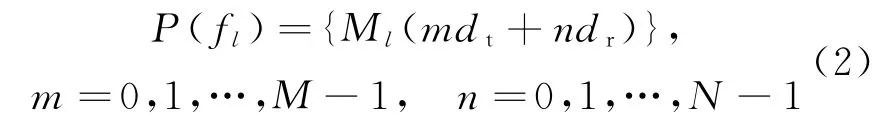
式中:M =f /为一个与载频和参考频率相关的固定常数。通过分析式(2)可知,仅仅使用个物理阵元就能获取一个孔径大小为M [(1)+(1)]=M M Nd的等效虚拟阵列。由于=,载频f 的等效阵列为一个均匀直线阵列。一般地,设置=/2,其中为参考频率对应的波长,此时载频f 的等效阵列为阵元间距为M λ/2的稀疏均匀直线阵列。
利用MIMO 阵列雷达同时设置接收阵列阵元间距为发射阵列天线孔径,每个载频f 都可以获得一个均匀直线等效阵列。该等效阵列单元数为,阵列导向矢量为
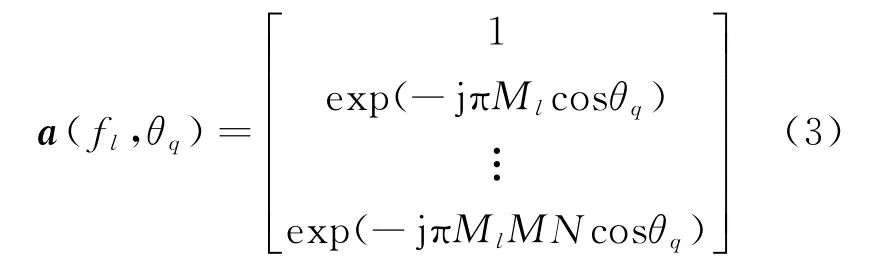
MIMO 等效接收阵列模型如图2所示。
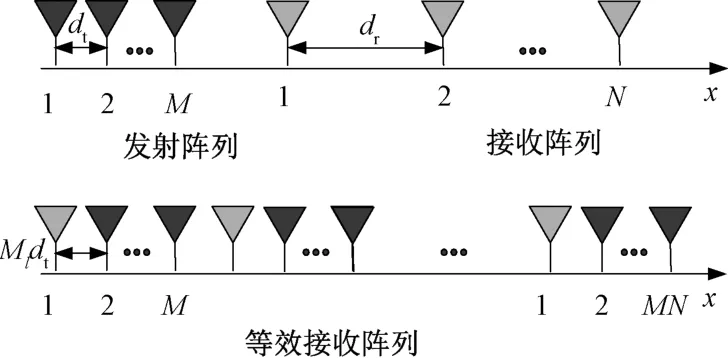
图2 MIMO 等效接收阵列模型
1.2 单载频自相关互质空间等效阵列模型
载频为f 的等效阵列接收信号矢量(f ,)的协方差矩阵为
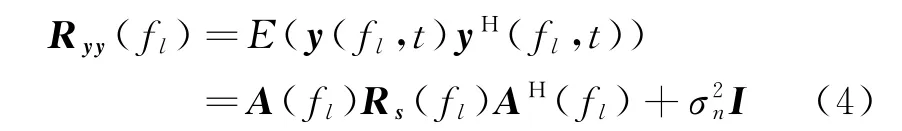
其中
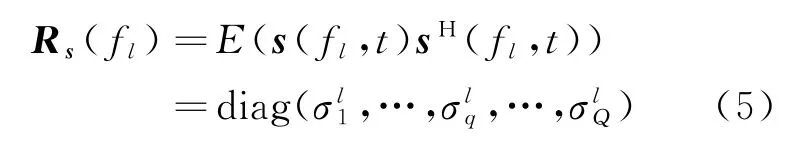
式中:(·)表示数学期望;H 表示矩阵共轭转置;R (f)为载频f对应目标回波信号的协方差矩阵;为单位矩阵;σ为第个目标在载频f照射下的回波功率;diag(·)表示对角矩阵函数。通过对协方差矩阵R (f )进行列向量化,可以获得互质空间接收信号矢量
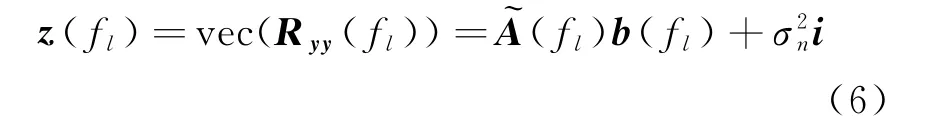

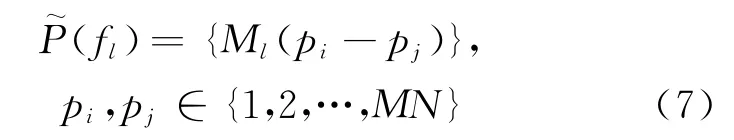
采用互质空间处理,每个载频可以获得的等效阵列阵元数目最大为21,进一步提升了系统的自由度。
1.3 多载频互相关互质空间等效阵列模型
根据以上分析,对两个载频f ,f 的等效阵列的接收信号矢量(f ,),(f ,)求取互协方差矩阵
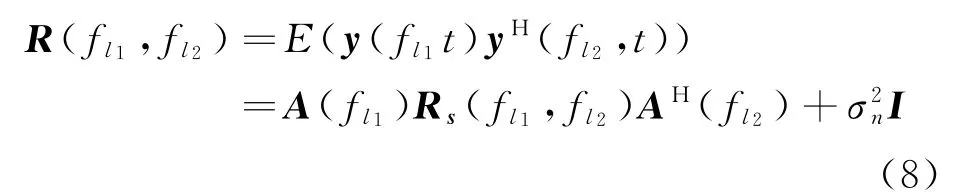
其中
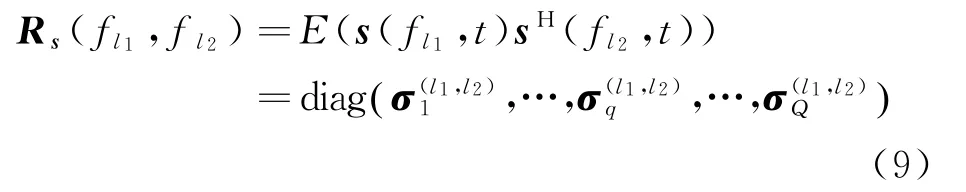
式中:为第个目标在载频f,f照射下的回波信号的互协方差矩阵。通过对协方差矩阵(f ,f )进行列向量化,可以获得互质空间接收信号矢量
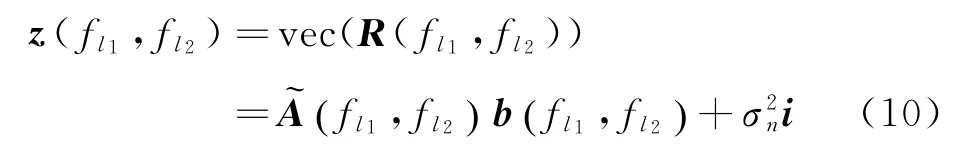
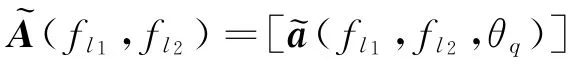
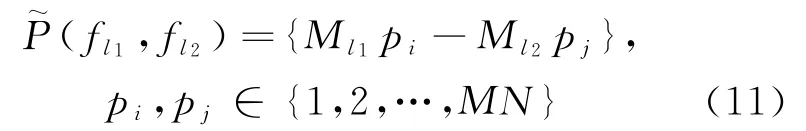
由于MIMO 系统采用了个互质载频,M ,M 两两互质,可最大程度减少重合位置。利用个互质载频,共计形成(-1)/2个互质载频组合,可以获得的互质空间等效阵列的最大自由度,即等效阵列的阵元数满足
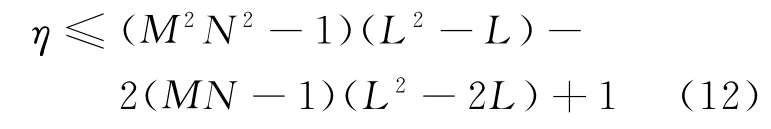
例如,取3,2,3,3,4,5时,MIMO 等效接收阵列的阵元数为6,多载频互质空间等效阵列的阵元数39,进一步提高了MIMO 系统的阵列自由度。图3给出了各种等效接收阵列阵元位置,其中归一化位置因子=/2。图3(a)为MIMO 等效接收阵列阵元位置集合,表明每个载频的等效阵列均为稀疏均匀阵列,单独对各个载频的接收信号进行DOA估计将存在空间角度模糊问题。图3(b)和图3(c)分别为多载频自相关及互相关等效稀疏非均匀直线阵列阵元位置集合,表明互质空间的等效阵列为稀疏非均匀直线阵列。该类阵列可以看作一个均匀直线阵列的子阵列,由于其内部存在不大于半波长的阵元间距,可以实现目标的无模糊角度估计。
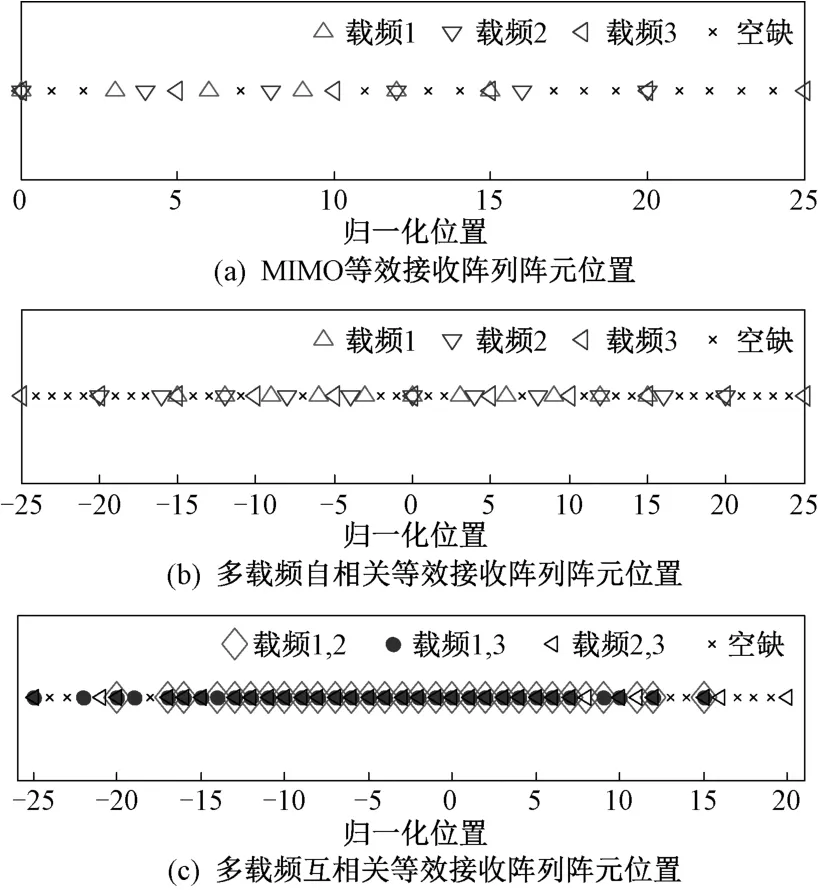
图3 MIMO 等效接收阵列模型
2 多载频互质空间DOA 估计
2.1 稀疏非均匀直线阵列单快拍DOA估计
通过以上分析可知,单载频自相关等效接收阵列和多载频互相关等效阵列的信号模型都为单快拍稀疏非均匀阵列接收信号模型。适应单次快拍的DOA 估计方法主要有前后向平滑(forwardbackward spatial smoothing,FBSS)方法、基于网格划分的压缩感知(compressive sensing,CS)方法以及无网格压缩感知(off-grid CS)方法。
FBSS方法只能利用稀疏非均匀等效阵列中的均匀子阵列部分,一方面使用的有效口径受限,角度分辨力差;另一方面,可用的阵列单元数少,不能充分利用等效阵列的孔径和自由度。
基于网格划分的压缩感知DOA 估计方法,如基追踪(basis pursuit,BP)方法、正交匹配追踪(orthogonal matching pursuit,OMP)方法等,不需要进行空间平滑处理,不受阵列形式限制,可以充分利用等效阵列的孔径和阵列自由度。但是该类算法需要对角度空间进行网格划分,同时假定目标的来波方向位于预先划分的网格上,受限于压缩感知的有限等距性质(restricted isometry property,RIP),网格的间隔不能太小,当目标不在网格上时,该类方法存在网格失配问题,其角度估计精度受限。
无网格压缩感知方法利用原子范数模型,不需要进行网格划分,从而解决了网格失配问题。该方法利用原子范数的最小化条件,将元均匀直线阵列单快拍DOA 估计问题转换成半正定规划(semidefinite programming,SDP)问题。其优化模型为

式中:max(·)为取最大值函数;Re(·)为取实部函数;为待优化的参数向量;为等效阵列单次快拍数据;为待优化的矩阵;Q 为矩阵的第行第列元素。
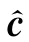
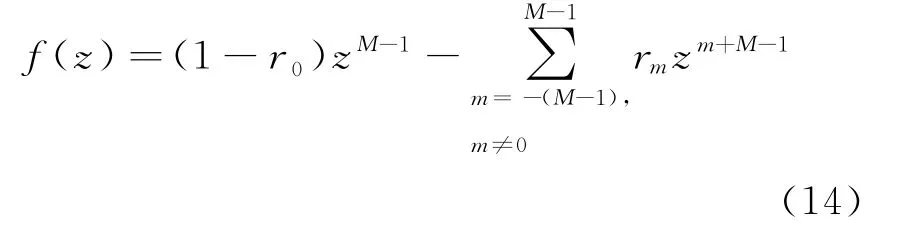
其中
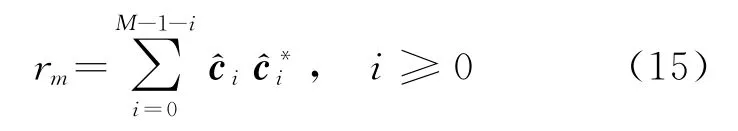
式中:,r 为求根多项式系数。通过求解()0,获取单位圆内部最靠近单位圆的个根,就能获得目标的DOA 估计值。
对于非均匀稀疏阵列,可将其看作均匀直线阵列的一部分,并对其空缺的位置进行置零处理。此时的优化模型可以改成
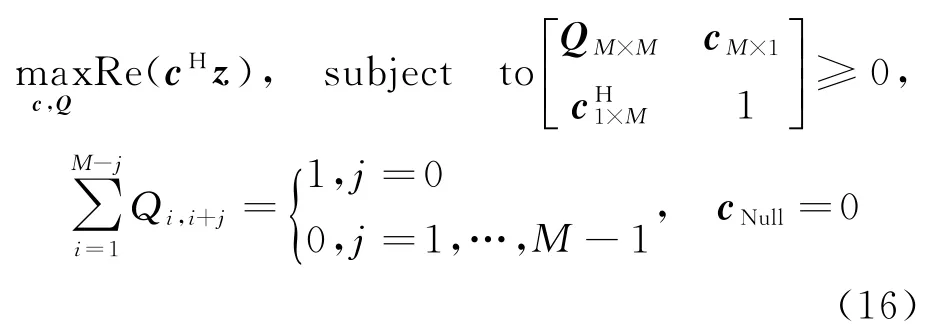
式中:为待优化的参数向量中缺失位置对应的元素。
采用与式(16)中同样的方式,可以求取稀疏非均匀直线阵列的个目标的DOA 估计值。
2.2 互质多载频等效阵列DOA估计
单个载频f 的自相关等效阵列接收信号(f )和载频f ,f 的互相关等效阵列接收信号(f ,f ),均可用无网格压缩感知算法进行DOA 估计。由于自相关等效阵列中阵元间距大,容易产生角度模糊问题。同时利用自相关等效阵列和互相关等效阵列接收的信息,可以消除空间模糊,同时提升DOA 估计性能。文献[8]采用了块压缩感知方法对所有的等效阵列进行联合优化求解,利用频率之间的联合稀疏特性提高DOA估计性能。这种方法主要的缺点是运算量大,存在网格失配问题。
为了解决分块压缩感知的网格失配问题,对稀疏非均匀直线阵列无网格压缩感知DOA 估计算法进行了拓展,提出一种多载频联合无网格压缩感知DOA 估计算法。其基本思路如下:首先利用稀疏非均匀直线阵列无网格DOA 估计方法中的优化步骤,求取所有自相关等效阵列和互相关等效阵列的参数向量,分别构建对应的求根多项式;再对所有的求根多项式求和,并对求和后的多项式进行求根处理,获取单位圆内部最靠近单位圆的个根,最终获得目标的DOA 估计值。
由于每个稀疏非均匀直线阵列的阵元数目不一样,有效孔径不一致,其求得的参数向量的阶数不同,不能直接对多项式进行求和处理。此时可将所有的等效稀疏非均匀直线阵列看成同一个均匀直线阵列的子阵列,在此基础上重新构建优化函数,使得各个阵列对应的优化参数具有相同的阶数,从而实现求根多项式的有效求和。采用与式(14)中同样的方式,可以求取稀疏非均匀直线阵列的个目标的DOA 估计值。
2.3 仿真分析
通过仿真验证所提方法的有效性。设MIMO 雷达的发射阵列阵元数3,接收阵列阵元数2,互质载频数=3,且3,4,5。所得到的3个自相关等效稀疏非均匀直线阵列阵元位置集合如图3(b)所示,得到的3个互相关等效稀疏非均匀直线阵列阵元位置集合如图3(c)所示。设置空域中6个远场非相干源,对应 的DOA 为[-60.3°,-36.2°,-12.1°,12.5°,36.5°,60.2°]。通过300次蒙特卡罗试验计算不同信噪比条件下的DOA 估计均方根误差,对比块压缩感知方法和本文方法的性能。块压缩感知方法采用的角度网格间距为0.2°,仿真结果如图4所示。
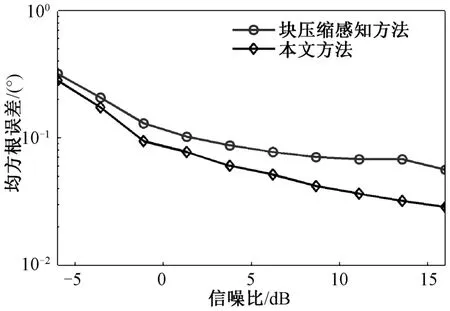
图4 测角均方根误差随信噪比变化对比
由图4可知,受限于网格失配,当信噪比较大时,块压缩感知方法的测角均方根误差随信噪比增大降低较慢,而本文方法的测角均方根误差随着信噪比增大稳定降低。在相同信噪比条件下,本文方法的测角精度更高。
3 结论
本文研究了互质多载频MIMO 雷达的DOA估计方法,并利用蒙特卡罗统计法仿真分析了基于无网格压缩感知的互质多载频等效阵列DOA估计方法的角度估计精度和通道信噪比的关系。研究表明:采用无网格压缩感知方法,可以充分利用互质多载频MIMO 雷达等效阵列的阵列孔径和自由度,同时可以避免块压缩感知所受网格失配的影响,可明显改善DOA 估计精度。

