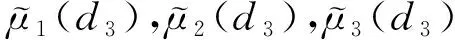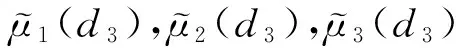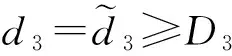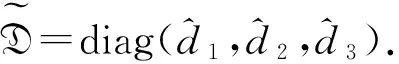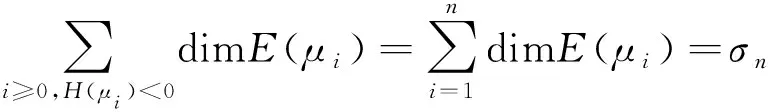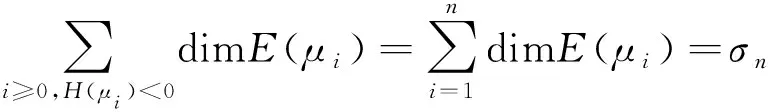一类带有食饵避难捕食-竞争扩散模型的定性分析
刘晓慧,王 静
(东北师范大学数学与统计学院,吉林 长春 130024)
1 预备知识
众所周知,扩散现象对于捕食者-食饵模型的动力学行为起着非常重要的作用.[1-3]因为种群的密度通常是空间不均匀分布的,扩散过程能更好地刻画出捕食者及食饵在不同的种群密度下种群数量流动的复杂性.考虑如下的种群模型:
(1)
其中:Ω∈RN(N≥1)是一个给定的有界光滑域;u1,u2是具有竞争关系的两个食饵;u3是捕食者;△是拉普拉斯算子;v是Ω边界上的单位外法向量;d1,d2,d3是正扩散系数;初始函数ui(x,0)(i=1,2,3)是连续函数.系统(1)是一个捕食竞争模型,在这个模型中,两个食饵是竞争关系,并且在竞争中第一个食饵u1比第二个食饵u2更有优势,这主要体现在α>1上.食饵u2有避难保护,即对捕食者免疫,使得捕食者u3只能捕食食饵u1.
本文研究系统(1)的正稳态解的存在性和不存在性,可转化为研究下面椭圆系统非常值正解的存在性与不存在性:
(2)
本文通过特征方程的方法得到系统(1)平衡点的局部稳定性;通过先验估计得到系统(2)的正稳态解的上下界;通过构造适当的V函数得到系统(1)的唯一正平衡点在一定的条件下是全局渐近稳定的;最后利用拓扑度理论对系统(2)的非常值正稳态解的不存在性和存性进行了研究.
2 反应扩散系统平衡点的局部稳定性
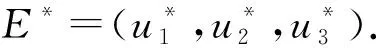
令0=μ1<μ2<μ3<…是满足Neumann边界条件、在Ω上-Δ算子的特征值,E(μi)是μi在C1(Ω)上相应的特征空间,定义集合



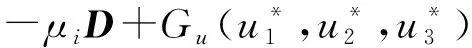
Ψi(λ)=λ3+B1iλ2+B2iλ+B3i.
其中:
B1i=μi(d1+d2+d3)+A1,
由文献[4],因为a11<0,a22<0,所以B1i,B2i,B3i>0.通过直接计算得
其中:
M1=(d1+d2+d3)(d1d2+d1d3+d2d3)-d1d2d3,
M2=A1(d1d2+d2d3+d1d3)-(d1+d2+d3)[a22d1+a11d2+(a11+a22)d3]+(d1d3a22+d2d3a11),
M3=A2(d1+d2+d3)-A1[a22d1+a11d2+(a11+a22)d3]-[(a11a22-a12a21)d3-a13a31d2].

由文献[4]可知A1A2-A3>0,于是对于所有的i≥0,均有B1iB2i-B3i>0.根据Routh-Hurwitz判别法,对每一个i≥1,Ψi(λ)=0的三个根λi1,λi2,λi3都有负实部,定理结论成立.
3 正稳态解的有界性
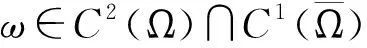
引理3.2(最大值原理)[6]令g(x,ω)∈C(Ω×R1),bj(x)∈C(Ω),j=1,2,…,N.
为了方便,定义常数(d1,d2,d3)=d,(a,b1,b2,d1,d2,k,l,m)=Λ.
定理3.1设D1,D2,D3是任意给定的正常数,则存在一个常数C=C(d,Ω,Λ),满足当K>Cα,且di≥Di(i=1,2,3)时,对系统(2)的任意解(u1,u2,u3)有
C-1 证明首先证明(u1,u2,u3)有上界,即ui 直接应用最大值原理得u2≤K.下证u1,u3有上界.设ω=cd1u1+d3u3,那么 由引理3.2, 取C充分大,则ui 其次证明(u1,u2,u3)有下界,即ui>C-1,i=1,2,3. 根据系统(1)的第一个方程,已知u1≠0,所以只需要考虑u2=0或u3=0的情况. 当i→∞时有 (3) 令u=(u1,u2,u3)是系统(1)的一个正解,ui>0,i=1,2,3. 证明首先构造V函数 由Green公式 所以 证明因为 (4) 选取足够小ε,使得 定理证毕. 首先研究系统(2)在u*处的线性化,设X定义同前,令 X+={u∈X|ui>0在Ω上,i=1,2,3}, B(C)={u∈X|C-1 其中C由前文给出.系统(2)改写为 (5) u是系统(5)的正解,当且仅当 F(u)≜u-(I-Δ)-1{D-1G(u)+u}=0 在X+中成立.这里(I-Δ)-1是(I-Δ)在带有Neumann齐次边界条件的X中的转置.因为F(·)是恒同算子的一个紧扰动,对任意B=B(c),若在∂B中F(u)≠0,可以定义Leray-Schauder度deg(F(·),0,B).记DuF(u*)=I-(I-Δ)-1{DGu(u*)+I},如果DuF(u*)是可逆的,F在u*处的指数就定义为index(F(·),u*)=(-1)γ,这里γ是DuF(u*)带有负实部特征根的总数.在讨论DuF(u*)的特征根时,将用到如下的分解 首先对任意i>0和1≤j≤dimE(μi),Xij在DuF(u*)下是不变的,且λ是DuF(u*)在Xij上的特征根,当且仅当它是如下矩阵的特征根: (6) 如果H(μi)≠0,那么对任意1≤j≤dimE(μi),DuF(u*)在Xij上负特征根的个数是奇数,当且仅当H(μi)<0. 引理6.1[7-8]假设对任意的i≥0,矩阵μiI-D-1Gu(u*)是非奇异的,则 index(F(·),u*)=(-1)σ, 这里 这个结论表明σ和γ奇偶性是相同的.为了计算(F(·),u*)的指数,需要考虑H(μi)的符号.直接计算得 det{μD-Gu(u*)}=A3(d3)μ3+A2(d3)μ2+A1(d3)μ-detGu(u*)≜A(d3;μ). (7) 其中: A3(d3)=d1d2d3,A2(d3)=-a11d2d3-a22d1d3, A1(d3)=a11a22d3-a13a31d2-a12a21d3. 计算得 如果参数Λ,d1,d2满足a11d2+a22d1<0,能得到以下命题: (8) 如果a11a22-a12a21<0,则 (9) 如果a11a22-a12a21>0,则 (10) 定理6.1假设参数Λ,di,i=1,2是固定的,a11>0,且满足下面的条件之一: 则存在一个正数D3,使得当d3≥D时系统(2)至少存在一个非常值正解. 证明如果a11a22-a12a21<0,由引理6.2知存在一个正常数D3,使得d3≥D3,且 (11) (12) 则u是系统(2)的一个非常值解,当且仅当它是系统(12)当t=1时的一个正解.显然u*是系统(12)对任意0≤t≤1唯一的正解.对任意的0≤t≤1,u是系统(12)的一个正解,当且仅当 F(t;u)≜u-(I-Δ)-1{D-1(t)G(u)+u}=0 在X+上成立. 显然F(1;u)=F(u),定理5.1表明当F(0;u)=F(u)=0时,u*在X+中有唯一的正解 DuF(t;u*)=I-(I-Δ)-1{D-1(t)Gu(u*)+I}. 特别地, DuF(1;u*)=I-(I-Δ)-1{D-1Gu(u*)+I}=DuF(u*). (13) 根据(9),(11)与(13)式, (14) 由引理6.2, index(F(1;·),u*)=(-1)γ=(-1)σn=-1. (15) 如果a11a22-a12a21>0,由引理6.2知存在一个正常数D3,使得当d3≥D3成立且 (16) 根据(10),(13)及(16)式, (17) 由引理6.2, index(F(1;·),u*)=(-1)γ=(-1)σn=-1. 同理 index(F(0;·),u*)=(-1)01. (18) 由定理3.1知存在一个正常数C,使得对任意的0≤t≤1,方程(13)的正解满足C-1 deg(F( 1;·),0,B(c))=deg(F(0;·),0,B(c)). (19) 另一方面,由假设,方程F(1;u)=0和F(0;u)=0在B(c)上有唯一的正解,因此由(15)和(18)式, deg(F( 0;·),0,B(c))=index(F(0;·),0,u*)=(-1)0=1, deg(F( 1;·),0,B(c))=index(F(1;·),0,u*)=(-1)0=-1. 这与(19)式矛盾,定理证毕. [参 考 文 献] [1] 叶其孝,李正元,王明新,等.反应扩散方程引论[M].北京:科学出版社,2011:38-176. [2] PENG R,WANG M X.Positive steady states of the Holling-Tanner prey-predator model with diffusion[J].Proc Roy Soc Edinburgh Sect A,2005,135:149-164. [3] PANG P Y,WANG M X.Non-constant positive steady-states of a predator-prey system with non-monotonic functional response and diffusion[J].Proc London Math Soc,2004,88(3):135-157. [4] VANGE RICHARD R.Predation and resource partitioning in one predator-two prey modle communities[J].The American Naturalist,1978,112:797-813. [5] LIN C S,NI W M,TAKAI I.Large amplitude stationary solutions to a chemotaxis systems[J].J Differential Equations,1988,72:1-27. [6] LOU Y,NI W M.Diffusion self-diffusion and cross-diffusion[J].J Differential Equations,1996,131:79-131. [7] KO W,RYU K.Qualitative analysis of a predator-prey model with Holling type Ⅱ:functional response incorporating a prey refuge[J].J Differential Equations,2006,231:534-550. [8] HENRY D.Geometric theory of semilinear parabolic equations[M].Berlin:Springer-Verlag,1993:8-137.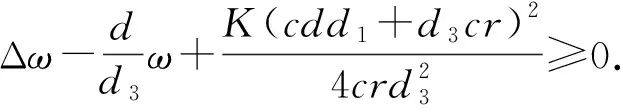


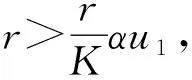

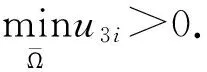
4 反应扩散系统平衡点的全局稳定性




5 非常值正稳态解的不存在性

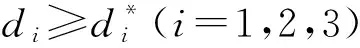

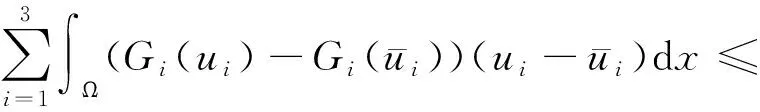
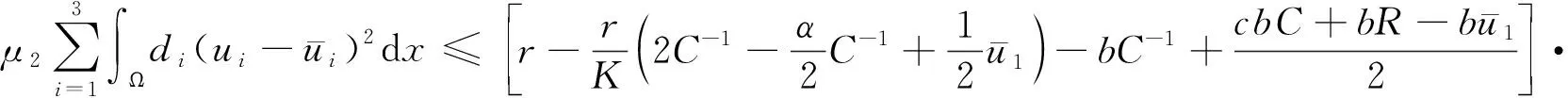
6 非常值正稳态解的存在性