图形的轴对称
高岚
(杭州市萧山区瓜沥镇第一初级中学,浙江杭州 311241)
1 教学的前端分析
1.1 学习内容分析
几何直观作为核心素养,是诱发学生创造能力的潜在因素,课程内容指出“借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的思路,预测结果。几何直观可以帮助学生直观地理解数学,在整个数学学习中都发挥着重要的作用。”《图形的轴对称》这一节是浙教版八年级上册第二章特殊三角形的第一节,对于学生培养几何直观起着重要作用,对后面进一步学习等腰三角形、直角三角形和圆的相关知识奠定基础。
1.2 学情分析
学生在小学已经学过一些平面图形的特征,形成了一定的几何直观,自然界和日常生活中也有许多具备轴对称性质的图形,这也为学生的学习奠定了感性基础。在知识水平上,八年级学生已经具备一定的观察能力,语言表达能力,在学习第一章全等三角形后,学生已具备一定的推理能力,因此对于本节课中轴对称图形的性质的得出需要一个比较复杂的探索过程,其中包括推理和表述这个难点,学生也具备了突破的能力。
2 教学目标
(1)了解轴对称图形的概念,了解两个图形成轴对称的概念。(2)理解轴对称图形的性质:对称轴垂直平分连结两个对称点的线段。(3)会判断一个图形是不是轴对称图形,并找出它的对称轴。(4)能画出简单平面图形关于给定对称轴的对称图形。
3 重点与难点
重点:图形的轴对称的概念和性质。
难点:轴对称图形的性质的得出需要一个比较复杂的探索过程,其中包括推理和表述,是本节教学的难点。
4 教学流程
4.1 情境引入,回顾旧知
视频展示G20天鹅湖片段,传达轴对称图形的美感,回顾轴对称图形、轴对称概念。让学生思考生活中、数学图形中的轴对称图形。
设计意图:通过视频,欣赏图片,寻找生活图形、数学基本图形让学生感受轴对称图形,体会轴对称图形与现实生活的紧密联系,激发学生的学习欲望,提高他们的学习积极性。
4.2 合作学习,探究新知
如图 1,AD平分∠BAC,AB=AC。

图1
(1)四边形ABDC是轴对称图形吗?如果你认为是,请说出它的对称轴。(2)将图形沿对称轴折叠后,哪些点会互相重合?(3)连结BC,交AD于点E,把四边形ABCD沿AD对折,BE与CE重合吗?∠AEB与∠AEC呢?(4)你可以发现AD所在的直线与线段BC之间的关系吗?
设计意图:学生通过观察、猜想、证明,得到线段、角之间的关系,并通过合作交流,将数学语言转化成文字语言,从而得到轴对称图形的性质。学生在自己掌握图形特征的基础上准确掌握轴对称图形的性质。培养学生合作精神和将图形语言转化成文字的能力。
4.3 性质运用,引出概念
如图2,已知△ABC和直线m。以直线m为对称轴,求作以点A,B,C的对称点A’,B’,C’为顶点的△ A’B’C’。
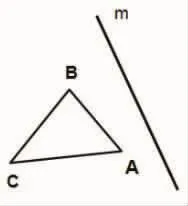
图2
设计意图:巩固运用性质画已知点的对称点,培养学生转化意识,将图形转化到关键点,将三角形类比到四边形、圆等图形。
4.4 习题分析,加深理解
如图3,已知直角三角形ABC,(1)以直角边AC所在的直线为对称轴,做出与直角三角形ABC成轴对称的图形。(2)第(1)题做出的图形和原三角形组成一个等腰三角形吗?请说明理由。

图3
设计意图:学生通过观察、思考、合作交流,从不同方面区别轴对称图形与图形的轴对称,鼓励学生善于思考、勇于发现,培养合作意识。
4.5 运用新知,解决问题
唐朝诗人李颀 《古从军行》有一个有趣的数学问题,诗中将军在观望烽火之后从山脚下的A点出发,走到河边m饮马后 再到B点宿营(图4),请问怎样走才能使总的路程最短?

图4
设计意图:体会图形的轴对称在现实生活中的广泛应用,感受最短路线的画法,化同侧为异侧,化折线为直线的基本图形,通过基本图形,把复杂的数学问题变得简明、形象,有助于学生探索解决问题的思路。
4.6 小结
(1)通过这节课,你学到了哪些概念?
(2)这些概念之间有什么区别和联系?
(3)如何画一个图形关于一条直线的轴对称图形?
(4)画轴对称图形的依据是什么?
带着这些问题,翻看课本,回顾本节课的知识点,并请学生归纳。
设计意图:本节课采用问题引领,带领大家一起回顾与整理课本内容,促使学生去发现新旧知识间的联系,主动构建新知结构,为今后学生的自主学习(复习)打基础。
5 教学反思
教学中通过优美的天鹅湖舞蹈引入,创设问题情境,激发学生探求知识的欲望,适时地让学生动手操作,合作学习,化静态图形为动态操作,使学生始终处于主动探索的积极状态,使不同层次的学生的知识水平得到恰当的发展和提高。图形的轴对称常出现在中考题中涉及折叠问题,最短路线问题,通过“将军饮马”问题帮助学生建立基本图形,将复杂的问题简单化,同时也让学生感受到图形的轴对称性在生活中的应用。
[1]曹文喜.利用几何图形的轴对称性解题[J].中学数学,2016(10):89-90.
[2]于志洪.用图形的轴对称性求线段和的最小值[J].现代中学生:初中学习版,2017(4):26-28.
[3]吴俊杰.图形的轴对称、中心对称[J].中学数学教学参考,2015(Z2):100-103.

