基于总类内分布的松弛约束双支持向量机

，

(北京科技大学 数理学院， 北京 100083)

支持向量机(support vector machine, SVM)[1]是模式识别领域中的一种有效算法， 最初由Cortes等[2]提出， 以解决二分类问题， 此后经过众多学者不断研究而迅速发展起来。 Mangasarian等[3]提出广义特征值近端支持向量机(generalized eigenvaluepro-ximal SVM, GEPSVM)， 首次通过构造2个非平行平面来处理二分类问题。 在此基础上， Jayadeva等[4]于2007年提出了双支持向量机(twin support vector machine, TWSVM)。与SVM相比，TWSVM求解的是2个小规模的二次规划问题(QPPs)而不是一个大规模的QPPs，这使得TWSVM的训练速度比SVM的更快。 受Fisher判别分析[5]的启发，将类分布信息引入SVM构造中开始普及。例如最小类方差支持向量机(minimum class variance SVM, MCVSVM)[6]、结构正则支持向量机(structural regularized SVM, SRSVM)[7]等。 同样， 将类分布信息引入SVM构造中在TWSVM领域也得到了发展。 例如， Peng等[8]提出了鲁棒最小类方差双支持向量机(robust minimumclass variance TWSVM, RMCV-TWSVM)，将正、负类样本点的类方差矩阵分别引入2个超平面的构造中。Qi等[9]提出了结构双支持向量机(structural TWSVM, S-TWSVM)，将正、负类样本各自聚类簇的协方差矩阵求和得到正、负类样本的协方差矩阵，分别参与构造分类超平面。以上2种算法都加入了类内结构信息,但是并没有将样本总的类内分布信息考虑到每个SVM的构造中。本文中将样本的总类内离散度矩阵加到每个SVM的公式中，这样构造超平面考虑得更加全面。同时，还可以解决线性RMCV-TWSVM中类方差矩阵不可逆的问题。虽然TWSVM算法在不断完善，但是在TWSVM领域，对于噪声处理的算法还不是很成熟。其中最基本的做法是在目标函数中引入样本的模糊隶属度来处理不同的样本。例如，Khemchandani等[10]提出模糊双支持向量机(fuzzy twin support vector machine, FTSVM)，根据距离理念来设计隶属度函数。丁胜锋等[11]提出基于混合模糊隶属度的FTSVM，将距离与紧密度相结合来设计模糊隶属度函数。由于目标函数对变化比较敏感，因此传统的算法可能会导致不理想的分类结果。基于以上分析，本文中提出一种新的方法来处理噪声样本，即松弛约束条件，不仅提出松弛约束的隶属度函数，而且将一对约束参数项引入到模型的构造中，以达到减少噪声值影响的目的。同时还考虑样本总的类内分布信息，最后提出一类基于总类内分布的松弛约束双支持向量机(TWCD-RTSVM)。

1　TWSVM模型

给定训练样本集T={(xj,yj),j=1,2,…,m}，其中xj∈n,j=1 ,2 ,…,m为行向量，表示样本的输入，yj={1, -1}为相应的类别， 当yi=1时样本属于正类， 当yj=-1时样本属于负类。 假设样本集中正、 负类的样本数分别为m1和m2，这里m=m1+m2。 不妨设xj(j=1, 2, …,m)为正类样本，xj(j=m1+1, …,m1+m2)为负类样本。 矩阵A∈m1×n和B∈m2×n分别为训练集正、负类样本构成的矩阵，CT=(ATBT)，C∈m×n为全体训练集样本构成的矩阵，且A和B的第i行Ai,Bi∈n分别为正、负类的样本点。

对于线性的情形，标准的TWSVM旨在寻找一对分类超平面

xTω1+b1=0，
xTω2+b2=0，

其模型为

(1)

式中：x∈n为列向量；法向量ω1,ω2∈n;b1,b2∈;c1,c2>0为惩罚参数；ζ1∈m2,ζ2∈m1为松弛向量；e1∈m1,e2∈m2为分量全是1的列向量。

通过引入Lagrangian函数，得到问题(1)的对偶问题，即

(2)

式中：H=(Ae1);G=(Be2)；α∈m2,γ∈m1为Lagrangian乘子。求得原问题的解为

新样本点x∈n的类别取决于决策函数

对于非线性的情形，需要利用核函数建立一对标准的TWSVM非线性分类超平面

K(xT,CT)u1+b1=0，
K(xT,CT)u2+b2=0，

式中：K为核函数，K(xT,y)=φ(xT)φ(y),x,y∈n为列向量，K(xT,CT)∈1×m的每个分量为实数，φ(·)为低维样本空间n到高维Hilbert空间H的一个非线性映射；为CT的第i列；u1,u2∈n为列向量。

非线性模型为

(3)

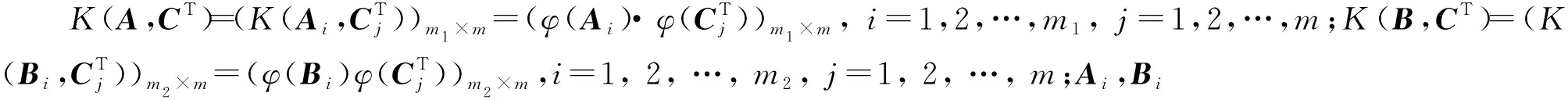
非线性模型的求解过程与线性模型的求解过程类似，求得原问题的解为

式中：S=(K(A,CT)e1)；R=(K(B,CT)e2)。

新样本点x∈n的类别决策函数为

2　TWCD-RTSVM的构造与求解

Shao等[12]在TWSVM算法被提出来后，提出了正则双支持向量机(twin bounded SVM, TBSVM)，其主要改进是在目标函数中加入了正则项，实现了结构风险最小化原则。下面将总类内分布因素(总类内离散度矩阵)引入到正则项中，使得2类样本在以最大限度分离的同时保证类内结构尽量紧密。

(4)

为了避免目标函数对数据变化过度敏感，对约束条件进行模糊设置，以一对约束参数项的形式体现在模型的构造中，以提高模型的抗噪声能力。再结合式(4)中的总类内离散度矩阵，提出新模型。

下面从线性和非线性2个方面提出TWCD-RTSVM模型。

2.1　TWCD-RTSVM线性模型

s.t.-(Bω1+e2b1)+ζ1≥E1,ζ1≥0

,

(5)

s.t.(Aω2+e1b2)+ζ2≥E2,ζ2≥0

,

(6)

其中E1∈m2、E2∈m1为各分量相等的约束参数向量(定义详见第3节)。

TWCD-RTSVM的第1项是结构正则项，实现了结构风险最小化原则。同时引入类内紧密性因素，使得TWCD-RTSVM的目标函数在理论上比TBSVM的目标函数更为理想。第2项是紧密项，最小化是为了保证超平面接近对应类的样本。第3项是错分项，最小化是为了降低另一类样本的错分程度。约束条件要求其中一类的样本以一定的误差尽可能远离另一类样本的超平面。

为了求解模型(5)、(6)，给出如下引理1、2及定理1。

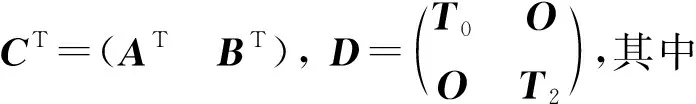
当m-2≥n时，如果r(C)=n且CT的第2列到第n+1列线性无关，则r(CTD)=n。

证明略。

引理2设Sw为样本的总类内离散度矩阵，根据式(4)，当m-2≥n时，如果r(C)=n且CT的第2列到第n+1列线性无关，则Sw为对称正定矩阵。

r(D)=r(T1)+r(T2)=(m1-1)+(m2-1)=m-2。当m-2≥n，r(C)=n且CT的第2列到第n+1列线性无关时，由引理1，r(CTD)=n，即Sw满秩，因此Sw是对称正定矩阵。

定理1在引理2的条件下，线性模型(5)、(6)的对偶问题分别为

s.t.0≤α≤c2e2

,

(7)

和

s.t.0≤γ≤c4e1

,

(8)

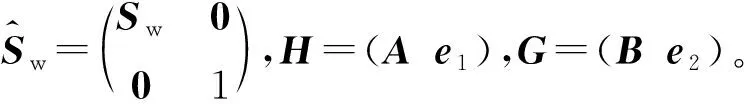
证明：优化问题(5)的Lagrangian函数为

L(ω1,b1,ζ1,α,β)=

αT[-(Bω1+e2b1)+ζ1-E1]-βTζ1,

(9)

对上式变量ω1、b1、ζ1求偏导并令其等于0，根据Karush-Kuhn-Tucker(简称KKT)条件可得

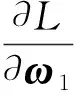
(10)

(11)

，

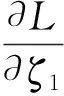
(12)

-(Bω1+e2b2)+ζ1≥E1,ζ1≥0

，

(13)

αT[-(Bω1+e2b1)+ζ1-E1]=0,βTζ1=0 ，

(14)

α≥0,β≥0

。

(15)

由式(10)、(11)得

(16)

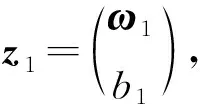
(17)

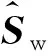
由式(17)得

(18)

将式(18)及KKT条件代入式(9)，可得问题(5)的对偶问题为

s.t.0≤α≤c2e2。

同理，得到问题(6)的对偶问题为

s.t.0≤γ≤c4e1,

以及

(19)

定理1得证。

由定理1，求解对偶问题可得到模型(5)、(6)的解z1和z2。对于新样本点x∈n，类别标签取决于决策函数

2.2　TWCD-RTSVM非线性模型

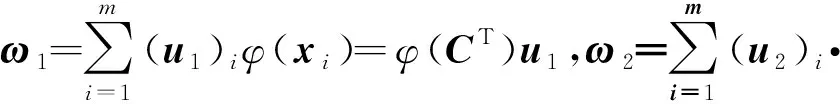
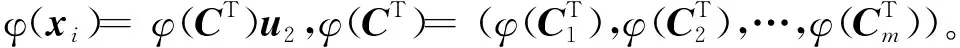
s.t.-(K(B,CT)u1+e2b1)+ζ1≥E1,ζ1≥0,

(20)

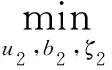
s.t.(K(A,CT)u2+e1b2)+ζ2≥E2,ζ2≥0。

(21)

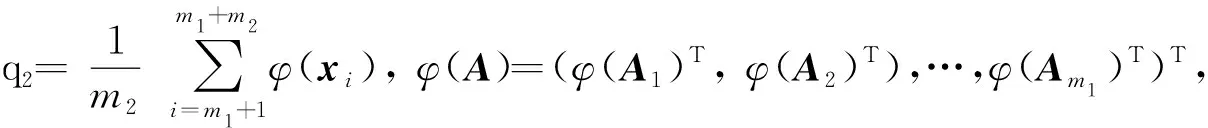
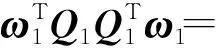
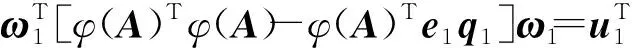
φ(A)φ(CT)-φ(CT)Tφ(A)Te1q1φ(CT)]u1=

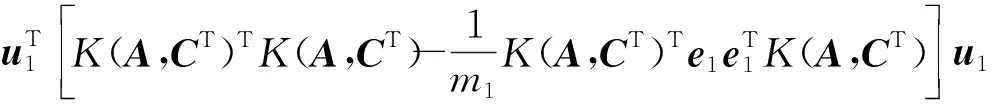
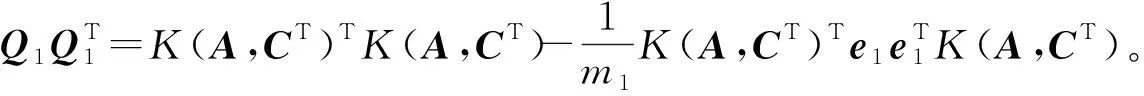
为了求解模型(20)、(21)，给出定理2，证明过程与线性情形的证明过程类似。

定理2非线性模型(20)、(21)的对偶问题分别为

s.t.0≤α≤c2e2

,

(22)

和

s.t.0≤γ≤c4e1

,

(23)

证明：通过lagrangian函数及KKT条件得

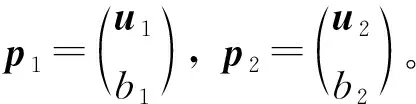
原问题的对偶问题为模型(22)、(23)。

由定理2，求解对偶问题可得到模型(20)、(21)的解p1和p2。对于新样本点x∈n，其类别决策函数为

3　约束参数项E1和E2的设置

在实际应用中，针对一些样本点(噪声点或离群值)不能被准确分类的情况，采取在约束条件中引入松弛约束的隶属度函数来减少噪声的影响。

对标准TWSVM模型(1)中的不等式约束进行如下处理，

(24)

(25)

基于文献[14]，对上述松弛约束进行处理，提出TWSVM松弛约束条件的隶属度函数。

定义1松弛约束的隶属度函数设在论域U1=n+1+m2上给定映射μ1∶n+1+m2→[0, 1]， 在论域U2=n+1+m2上给定映射μ2∶n+1+m1→[0,1]，μ1和μ2分别定义为

μ1(ω1,b1,ζ1)=

μ2(ω2,b2,ζ2)=

则称μ1和μ2分别为松弛约束条件(24)和(25)的隶属度函数。其中d1和d2分别为模型(1)中2类不等式约束集允许违反的程度。

定义2松弛约束的α截集对∀α∈[0,1]，称集合

P1(α)={(ω1,b1,ζ1)∈n+1+m2|μ1(ω1,b1,ζ1)≥α},

P2(α)={(ω2,b2,ζ2)∈n+1+m1|μ2(ω2,b2,ζ2)≥α}

分别为松弛约束条件(24)、(25)的α截集。

由定义2，分别选取松弛约束条件(24)的α1截集和松弛约束条件(25)的α2截集，即有

-(Bω1+e2b1)+ζ1≥e2[1-d1(1-α1)]，

Aω2+e1b2+ζ2≥e1[1-d2(1-α2)]。

取约束参数向量E1=e2[1-d1(1-α1)]=e2v1，E2=e1[1-d2(1-α)]=e1v2，则得到TWCD-RTSVM模型的约束参数向量。

对于给定的(ω1,b1,ζ1)∈n+1+m2(或(ω2,b2,ζ2)∈n+1+m1)，d1(或d2)越大，负类样本(或正类样本)违反约束的程度越大，此时一些训练数据可视为噪声值或者异常值。αi(i=1,2)为松弛约束条件(24)、 (25)隶属度的下限，αi(i=1,2)越大， 则隶属度取值越大， 样本的确定性越高， 样本是噪声值的可能性越小。 当对正、 负类样本赋予相等的松弛程度(d1=d2)时， 如果α1>α2， 则v1>v2， 从而负类样本远离正类样本的程度大于正类样本远离负类样本的程度， 正类样本的确定性高于负类样本的，反之亦然。

综上所述，di和αi(i=1, 2)的不同取值， 即vi(i=1,2)的不同取值， 会对分类噪声值或者异常值产生一定的影响， 即对vi(i=1,2)合理取值能减少噪声值或者异常值对分类结果的影响， 从而提高分类精度。 在第4节中将利用数值实验来验证该结论。

4　实验与分析

4.1　评价标准

混淆矩阵[15]和受试者工作特征(receiver operating characteristic，ROC)曲线[16]是测量分类正确率的常用方法。混淆矩阵通过样本的真实结果与分类器预测的结果来计算正确率，混淆矩阵的结构见表1。

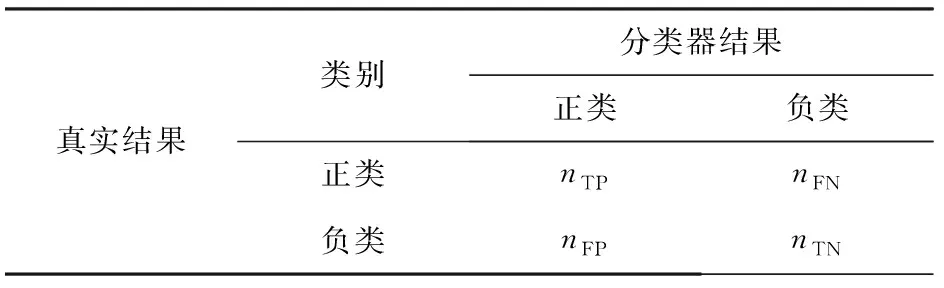
表1　混淆矩阵的结构

注：nTP和nTN分别为正、负类样本被分类器正确分类的样本数；nFP为分类器将负类样本误分成正类样本的样本数；nFN为分类器将正类样本误分成负类样本的样本数。

分类正确率为所有样本中被正确分类的样本所占的比例，即

式中：a为分类正确率；nTP和nTN分别为正、负类样本被分类器正确分类的样本数；nFP为分类器将负类样本误分成正类样本的样本数；nFN为分类器将正类样本误分成负类样本的样本数。

从混淆矩阵中还可以计算出假正率(false positive rate，FPR)和真正率(true positive rate，TPR)，即

式中：fFPR为假正率；fTPR为真正率。

ROC曲线描述的是分类混淆矩阵中FPR和TPR这2个量之间的相对变化情况。在TPR随着FPR不断增大的情况下，如果TPR增长得比FPR快，那么曲线靠近图形左上角的程度越大，曲线下的面积(area under the curve, AUC)越大，模型的分类性能也就越好，因此，可以通过计算AUC值来判断分类器的性能。

4.2　TWCD-RTSVM模型实验

选用UCI机器学习库中的6个数据集进行数值实验，即Hepatitis、Glass、Heart-statlog、Ecoli、BUPA和Monk_3，其中Glass和Ecoli为多分类数据集。由于本文中模型针对的是二分类问题，因此对多分类数据集Glass和Ecoli进行处理。取Glass集的类7为正类，其余各类归并成负类；把Ecoli集的Cp类和Im类归并成正类，其余各类归并成负类。将以上2类重新命名为Glass7和Ecoli12。6个数据集的详细信息见表2。

表2　数据集描述

通过混淆矩阵求解各分类器在上述6个数据集上的线性和非线性分类效果，实验结果分别见表3、4，其中分类正确率的最大值用黑体标出。由表3、4可知：1)在时间方面，TWSVM算法的耗时明显少于SVM的。与其他4种TWSVM算法相比，本文中所提算法TWCD-RTSVM的运行时间不相上下，在个别数据集上甚至耗时最少。总之，TWCD-RTSVM分类算法具有较高的分类效率。2)在正确率方面，无论是线性模型还是非线性模型，与其他分类算法相比，TWCD-RTSVM在上述数据集中的表现较好，分类正确率最高。在某些数据集上，个别分类算法与TWCD-RTSVM具有同样高的分类精度。例如，在Monk_3数据集中，RMCV-TWSVM与TWCD-RTSVM分类正确率相等，且都达到最高；在Glass7数据集中，TWCD-RTSVM甚至与多个分类算法都达到最高分类正确率。另外，与FTSVM相比，TWCD-RTSVM分类正确率较高，即抗噪声性能优于FTSVM的。总之，TWCD-RTSVM有很高的分类正确率及减噪能力。

实验过程中线性算法的最优参数见表5，其中，TWCD-RTSVM算法给出了使得不同数据集取得较好分类性能的参数v1和v2。前4个数据集在v1和v2取值不断变化时分类正确率的直观变化示意图见

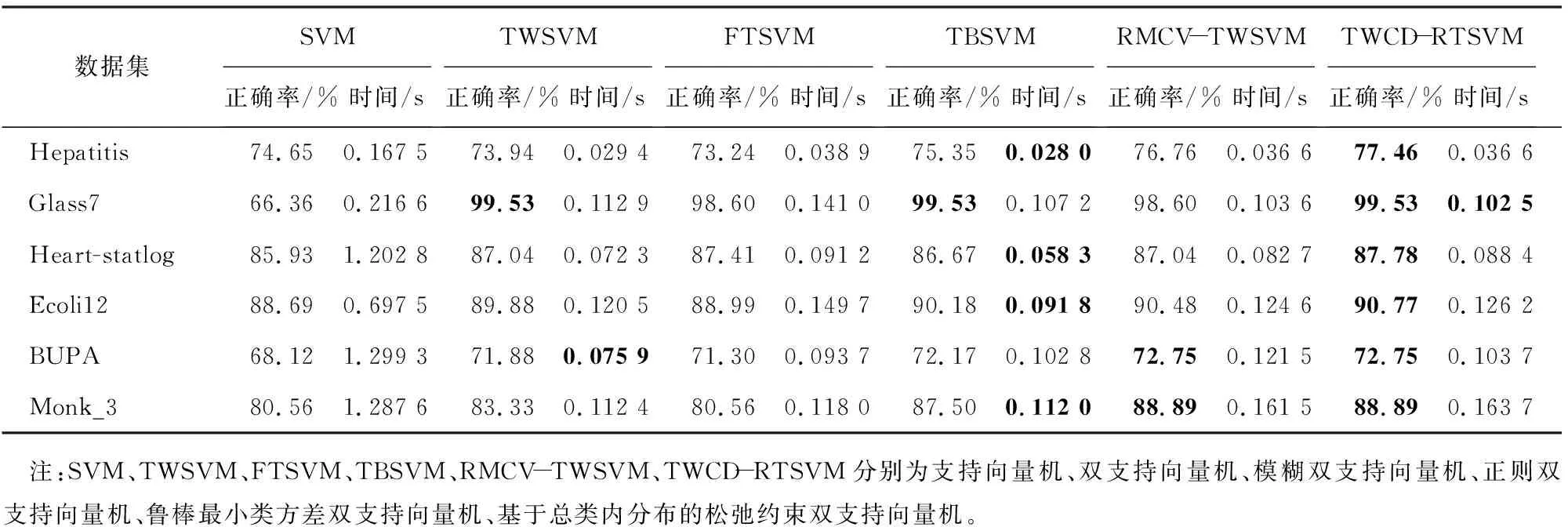
表3　各分类器的线性分类效果

表4　各分类器的非线性分类效果

图1。由图可知，4个数据集取得的最大分类正确率与最优参数值与表5中的数值相一致。对于Hepatitis和Heart-statlog数据集来说，当v1和v2取值较大(接近1)时，TWCD-RTSVM算法表现出较好的分类性能；对于Glass7和Ecoli12数据集来说，当v1和v2取值较小(小于0.5)时，TWCD-RTSVM算法已经表现出较好的分类性能，且在v1和v2的大部分取值范围内TWCD-RTSVM算法保持了较高的分类正确率，即算法比较稳定。

在ROC分析中， 通过求AUC值来测量分类算法的性能， AUC值越大， 说明分类算法越好。 为了实验简便， 模型中涉及的惩罚参数取值均为1。 求得上述各数据集在TWSVM、 FTSVM、 TBSVM、 RMCV-TWSVM和TWCD-RTSVM 5种线性TWSVM算法下的AUC值情况见表6，其中AUC最大值用黑体标出。由表可知，TWCD-RTSVM在上述数据集中的表现较好， 代表分类性能的AUC值最大。 在Monk-3数据集中， TWCD-RTSVM与TWSVM模型的AUC值相等， 且都达到最大值。

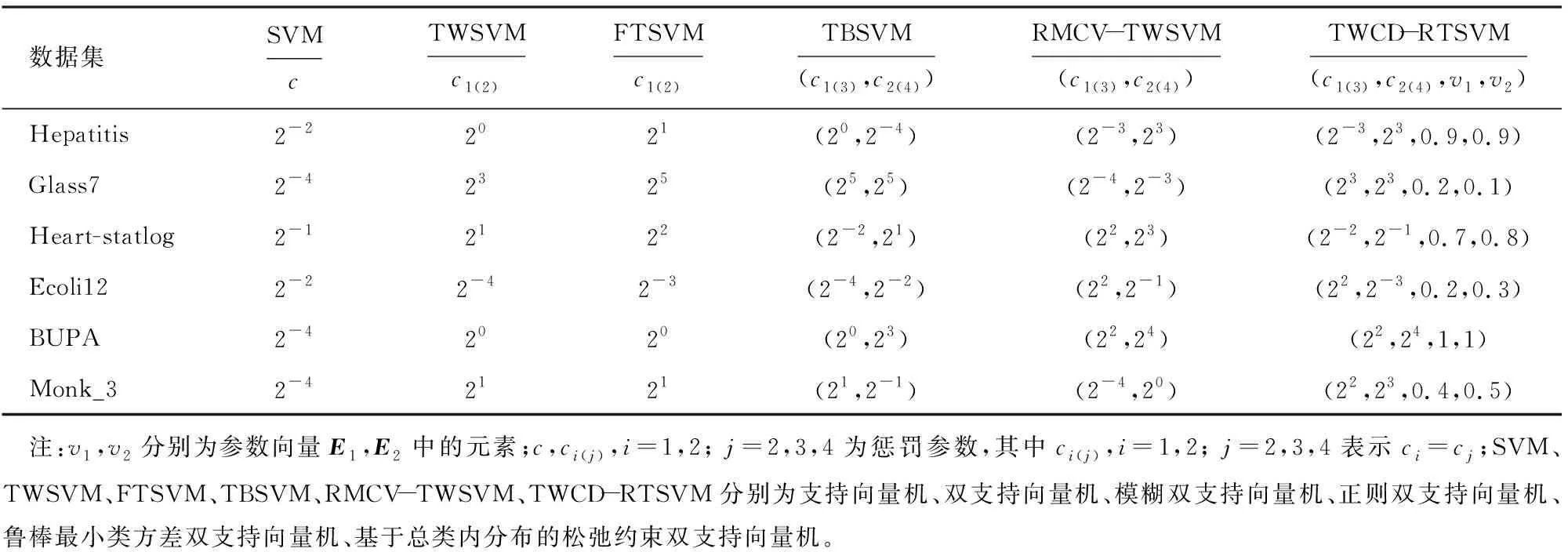
表5　各分类器的最优参数

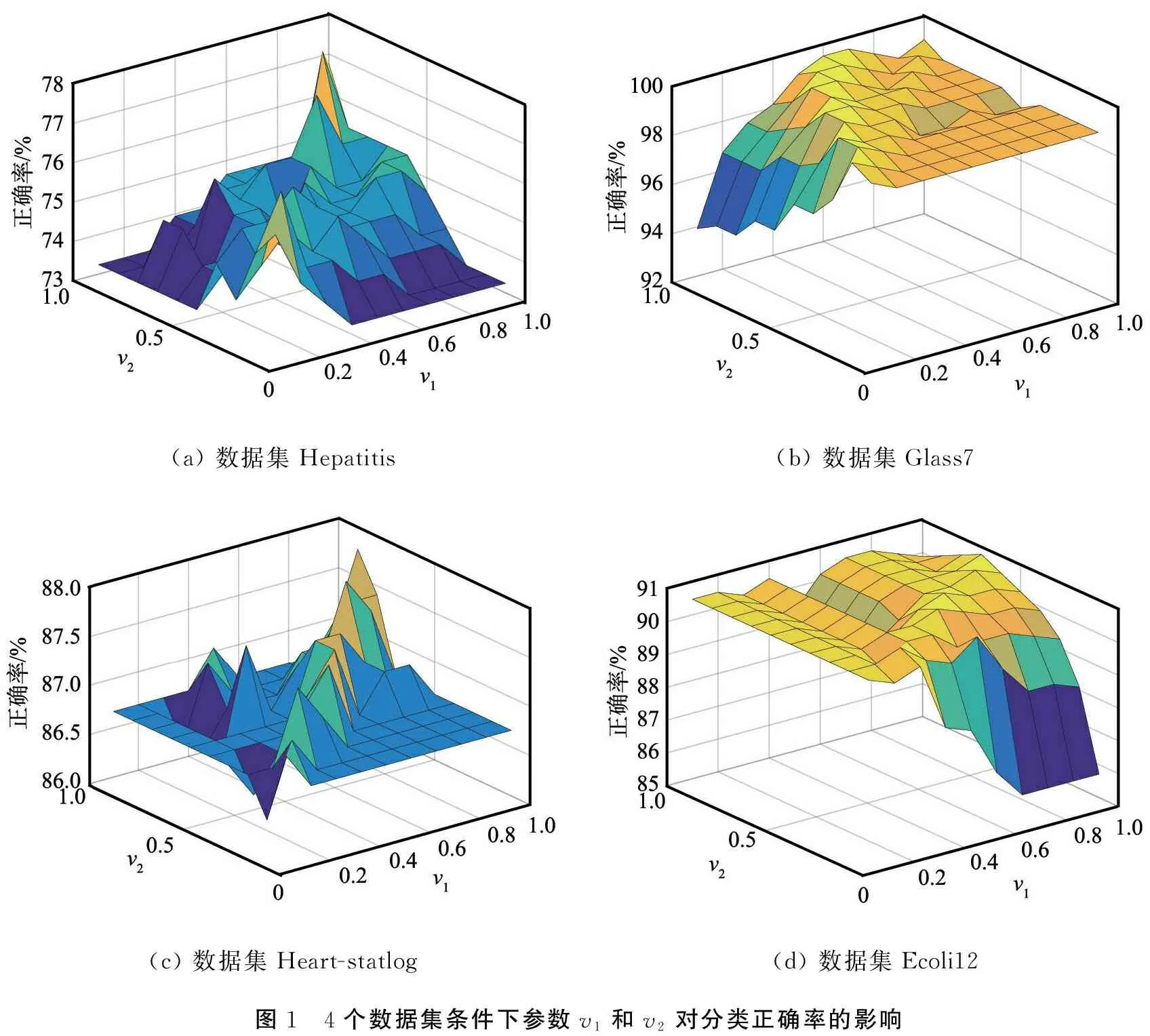
(a) 数据集Hepatitis(b) 数据集Glass7(c) 数据集Heart-statlog(d) 数据集Ecoli12图1 4个数据集条件下参数v1和v2对分类正确率的影响

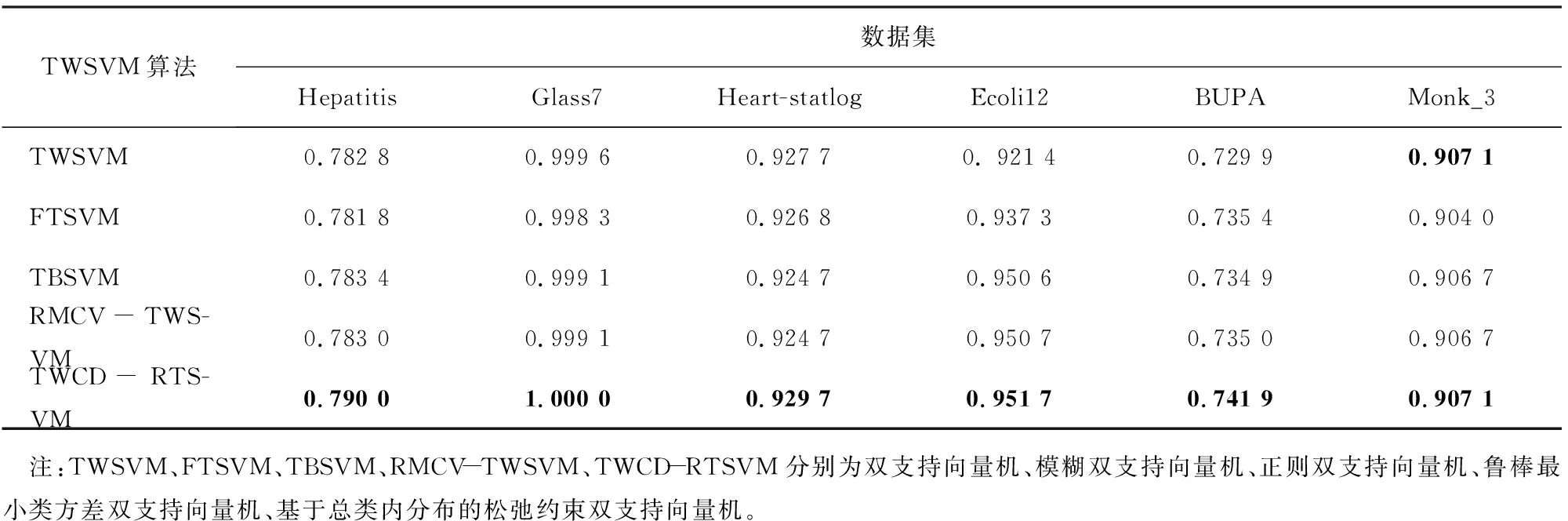
表6　5种TWSVM算法在6个数据集上的AUC值

5　结论

本文中提出了一种TWCD-RTSVM模型。主要结论如下：

1)该模型从模糊集的思想出发，对部分约束不等式集进行松弛处理，提出松弛约束的隶属度函数，进而构造出一对约束参数项来松弛约束条件，使得参数项合理取值后达到了减少噪声影响的目的。同时将整体类分布信息引入到模型的正则项中，实现了结构风险最小化原则。实验结果表明，TWCD-RTSVM算法具有较好的分类性能。

2)TWCD-RTSVM与4种TWSVM算法的对比实验结果表明，约束参数项和总类内分布信息的引入使得TWCD-RTSVM算法不仅分类正确率最高，而且具有较强的鲁棒性。在以后的研究中应致力于进一步探索参数项的构造与选择，以及将其应用到多分类问题。