基于变分模态分解排列熵和粒子群优化支持向量机的滚动轴承故障诊断方法

, ,

(1. 石家庄铁道大学 电气与电子工程学院, 河北 石家庄 050043; 2. 中车青岛四方机车车辆股份有限公司, 山东 青岛 266111)

滚动轴承在转动时一定会伴有振动。因轴承自身的结构及装配原因或受外部因素影响等产生的振动信号通常都是平稳的随机信号，但在轴承发生故障时，其信号是非平稳的时变信号。由于故障导致振动剧烈，在故障点处会有冲击产生，且持续时间非常短，混杂在正常信号中很难识别，因此要想在时域和频域精确诊断轴承状态是比较困难的[1-2]。

经验模态分解(empirical mode decomposition, EMD)算法[3]的提出给人们很大启发，目前该方法应用广泛，它的优点在于能够自适应地处理信号，通过按频段的信号分解方法将非平稳信号转换为平稳信号。左庆林等[4]在共振解调的基础上应用EMD对信号预处理，极大地增强了对噪声的抑制效果，但仍然没有解决共振解调中滤波器参数选择问题。蔡艳平等[5]结合EMD和谱峭度法实现了滚动轴承早期故障诊断，提高了抗噪能力，并解决了共振解调的带通滤波器参数的选取问题，但EMD存在模态混叠导致信号分解时频率不能完全分离的问题。张玲玲等[6]利用集成经验模态分解(ensemble empirical mode decomposition, EEMD)来减小EMD模态混叠现象的影响，将其应用于电机曲轴故障诊断，成功提取出轴承各状态特征，诊断精度更高。EEMD在一定程度上抑制了EMD的模态混叠；但是，由于引入了高斯白噪声，损害了信号纯洁性，因此导致分解所得的本征模态分量(intrinsic rnode functions, IMFs)成分杂乱。为了解决这个问题，2014年Konstantin等创造性地提出了变分模态分解(varianational mode decomposition, VMD)方法，该方法能够自适应地进行信号的频域剖分及各分量的有效分离。唐贵基等[7]将VMD和包络解调相结合对滚动轴承故障信号进行分析，证明了该方法的有效性。

支持向量机(support vector machine, SVM)[8-9]通过核函数将输入特征向量映射到高维特征空间，选择一个最优超平面进行数据分类，该方法的关键问题是对核函数最优核参数及其惩罚系数的选择。Yuan等[10]采用人工免疫算法来优化径向基以及多项式混合核函数，然后将优化后的SVM用于涡轮泵转子的故障诊断，结果表明，优化后的SVM诊断结果更准确，但该方法不适用于非线性分类问题。袁浩东等[11]通过粒子群算法对其进行了改进，将其应用于轴承早期微弱故障信号的诊断并取得了良好的效果。

考虑到VMD可以将非平稳信号分解转化成若干个平稳模态分量，粒子群优化支持向量机(particle swarm optimization-support vector machine, PSO-SVM)在小样本、非线性和高维模式识别问题中优势明显，本文中提出了VMD排列熵结合PSO-SVM的滚动轴承故障诊断方法，从包含有主要故障信息的IMFs中提取出时间序列特征，据此建立SVM故障诊断模型，并利用粒子群算法优化其参数，以识别轴承状态，最后通过实验验证该方法的准确性。

1　变分模态分解原理

VMD是通过迭代过程求解变分问题的方法，以经典维纳滤波、希尔伯特变换和混频处理为理论基础，自适应地将信号分解为一系列IMFs[12-14]。

在对信号分解的过程中，各个模态分量的中心频率和带宽随之变化，VMD以最小带宽和为条件筛选出K个模态函数uk(t)，k∈{1,2,…,K}，并用这K个函数的和代替原始信号f(t)。

假设原多分量信号由K个有限带宽的本征模态分量uk(t)构成，约束变分模型为

(1)

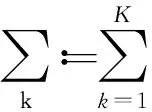
对于该模型，首先通过希尔伯特变换求uk(t)的解析信号进而得到其单边谱，再将其与指数因子e-jωkt相乘，将各模态频谱调制到相应的基频带。通过扩展的Lagrange函数将此约束变分问题转化为非约束变分问题进而求解，表达式为

L({uk},{ωk},λ)∶=

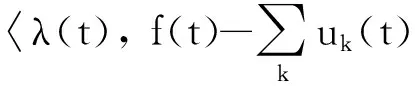
(2)

式中：α为二次惩罚因子；λ(t)为Lagrange乘法算子。

利用乘子交替方向算法求此Lagrange鞍点，就是原变分模型的最优解。求解过程中，各频域模态按式(3)进行更新。

(3)

(4)

,

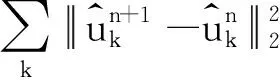
(5)

式中：ε>0， 为预定的判别精度；n表示更新次数。

2　排列熵原理

设一维特征向量[15]

X=(X(1),X(2),…,X(n))

，

(6)

根据相空间重构延迟坐标法对X中任一元素X(i)重构，对每个采样点取其连续的m个样点，得到X(i)的m维空间的重构向量

Xi=(x(i),x(i+1),…,x[i+(m-1)l])

。

(7)

则X的相空间矩阵为

(8)

式中m和l分别是重构维数和延迟时间。

对X的重构向量Xi各元素升序排列，可得

Xi={x(i+(j1-1)l)≤x(i+(j2-1)l)≤…≤

x(i+(jm-1)l),

(9)

式中j1,j2,…,jm为重构分量各元素所在列序号。

由此得到的排列方式为

{j1,j2,…,jm}

。

(10)

式(10)为全排列m中的一种，对X序列的所有排列情况进行统计，计算出所有排列情况出现的相对频率并将其视为概率P1、P2、…、Pk，k≤m，计算序列归一化后的排列熵H为

(11)

排列熵H表征时间序列的随机程度，其值越大表明该时间序列随机性越强，反之则越规则。

3　粒子群优化支持向量机原理

SVM方法最早由Vapnik等在20世纪90年代初提出，大致原理如下。

在高维空间里构造的优化问题为

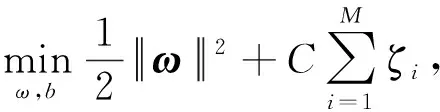
(12)

式中：xi∈n;yi∈{-1,1};ω为权重向量；b为最优超平面偏移量；ζi为松弛变量；C>0， 为惩罚参数;i=1,2,…,M。

决策函数为

(13)

式中K(xi,xj)为核函数。本文中使用高斯径向基函数作为核函数，

(14)

式中σ为核函数的参数。

Pbest代表粒子个体极值点位置，Gbest代表种群全局极值点位置，C为惩罚参数；g为核函数参数。图1　粒子群优化支持向量机方法流程图

SVM参数对其分类精度的影响很大，SVM参数C、σ严重影响分类精度η。为解决C、σ不易选择的问题，本文中提出用粒子群优化(particle swarm optimization，PSO)算法来确定SVM参数。图1为基于PSO的SVM参数优化过程。PSO算法的优势在于粒子不必进行交叉及变异运算，只需根据内部速度就可更新，算法速度快，便于实现。

4　基于变分模态分解排列熵和粒子群优化支持向量机滚动轴承故障诊断方法

该方法首先求得所有IMFs[16]的排列熵，然后将其作为特征向量输入SVM。此方法流程图大致如图2所示。

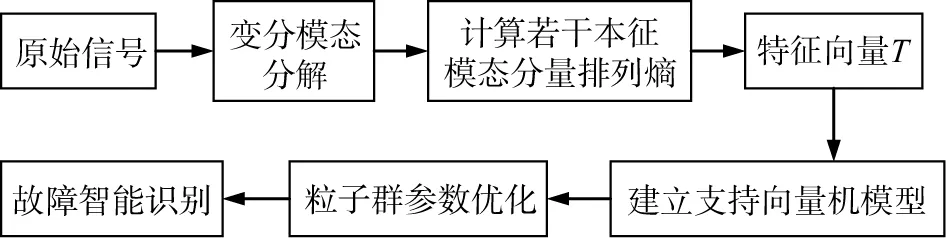
图2　基于变分模态排列熵和粒子群优化支持向量机故障诊断流程图

其具体步骤如下：

1)以同样的采样频率fs对轴承正常状态以及内圈、外圈和滚动体故障状态分别进行N次采样，共得4N组数据样本。

2)分别对每个状态下的振动信号进行VMD，分解后可得许多个IMFs，信号不同，其IMFs个数也不同，本文中研究的是那些包含故障信息的前m个IMFs。

3)计算所选出的IMFs的排列熵，并构建排列熵特征向量T，

(15)

T=(H1,H2,…,Hm)

。

(16)

4)针对1)中的小样本数据建立多故障分类器，用粒子群算法对SVM进行参数优化。

5)把轴承故障信号的IMFs能量特征向量T作为输入信号送给SVM，再对其进行测试。

6)经过上述过程可得SVM的输入，构造SVM故障诊断模型，根据决策函数f(x)判断轴承状态。

5　实验验证

本文中以QPZZ-Ⅱ旋转机械故障模拟试验台为实验对象，如图3所示，轴承转速314 r/min。

以25 600 Hz的采样频率分别在滚动轴承正常、外圈故障、内圈故障和滚动体故障状态下各采集20组数据，在这4种状态下，各随机抽取10组数据用于训练，其余的10组数据用于测试。

图3　QPZZ-Ⅱ旋转机械故障模拟试验平台

首先处理训练数据，对其进行VMD。为了节省篇幅，本文中只给出外圈故障数据的VMD结果，如图4所示。 由图中波形及频谱可以看出， 前面的几个IMFs包含的故障信息丰富， 本文中取前5个模态求其排列熵， 构造特征向量。 其他状态下的VMD处理同此。然后将提取出来的特征向量输入到PSO-SVM进行训练，支持向量机参数[Cσ]=[65.635.7]。最后，计算出所有状态下的测试数据对应的特征向量，全部输入到训练好的PSO-SVM中，实现故障模式识别。结果如图5所示，图中的横坐标表示样本点，空心圆代表实际测试集分类点，实心点代表预测测试集分类点，实际测试和预测测试各40个点，均为每10个样本点一组，共分4组，1—10点为正常，11—20点为外圈故障，21—30点为内圈故障，31—40点为滚动体故障。纵坐标的类别标签表示决策函数输出值，表1给出了决策函数f(x)值与故障类型对应关系。从图5可以看出，本文中所提方法故障诊断结果很精确，准确率高达92.5%。

(a) 波形

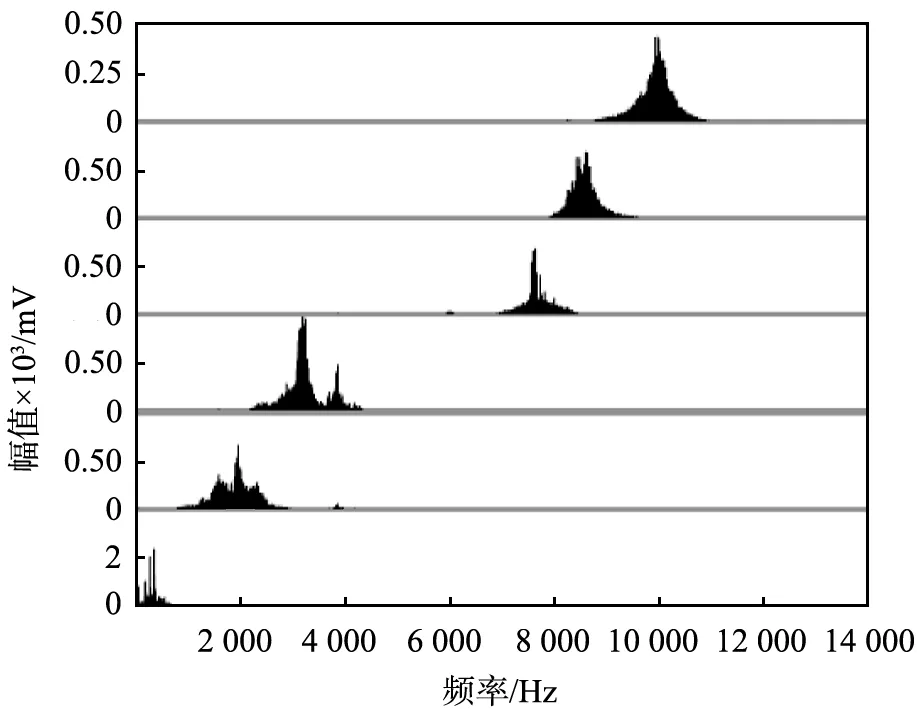
(b) 频谱图4　变分模态分解模态分量波形及频谱

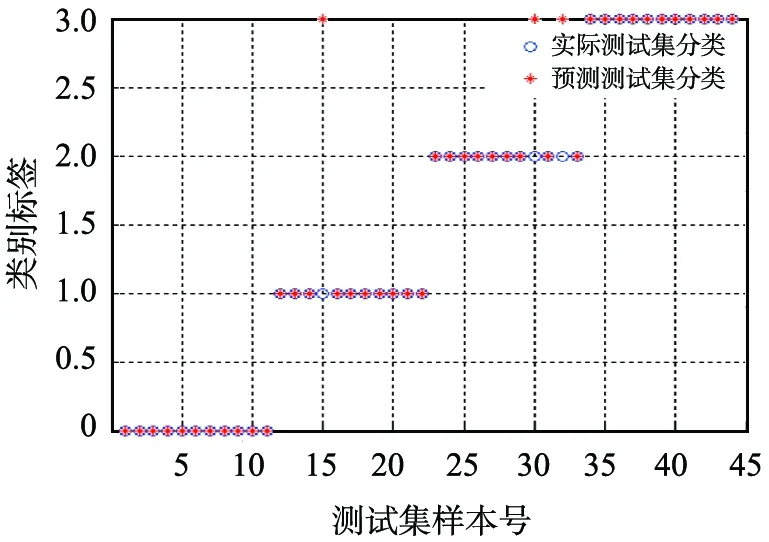
图5　变分模态分解结合粒子群优化支持向量机分类结果示意图

f(x)0123故障类型正常外圈故障内圈故障滚动体故障

为了突出本文中提出的方法的优势， 选择2种比较有代表性的方法进行对比实验， 一种为VMD结合SVM方法， 另一种为EEMD结合PSO-SVM方法。 图6为VMD结合SVM方法的故障分类结果， 可见其预测结果与实际存在很大偏差， 经计算准确率只有47.5%， 明显与本文中提出的方法差距较大； 在EEMD结合PSO-SVM方法的实验中， SVM参数[Cσ]=[45.3 30.4]。 图7为外圈数据进行EEMD所得的波形和频谱， 最终故障分类结果如图8所示， 经计算， 准确率为82.5%， 仍较本文中提出的方法低10%。 其主要原因在于EEMD的模态混叠干扰了SVM的故障识别， 而VMD却能很好地解决此问题。 由此可以证明本文中提出的方法行之有效， 能够以较高的准确率诊断轴承故障。

图6　变分模态分解结合支持向量机分类结果示意图

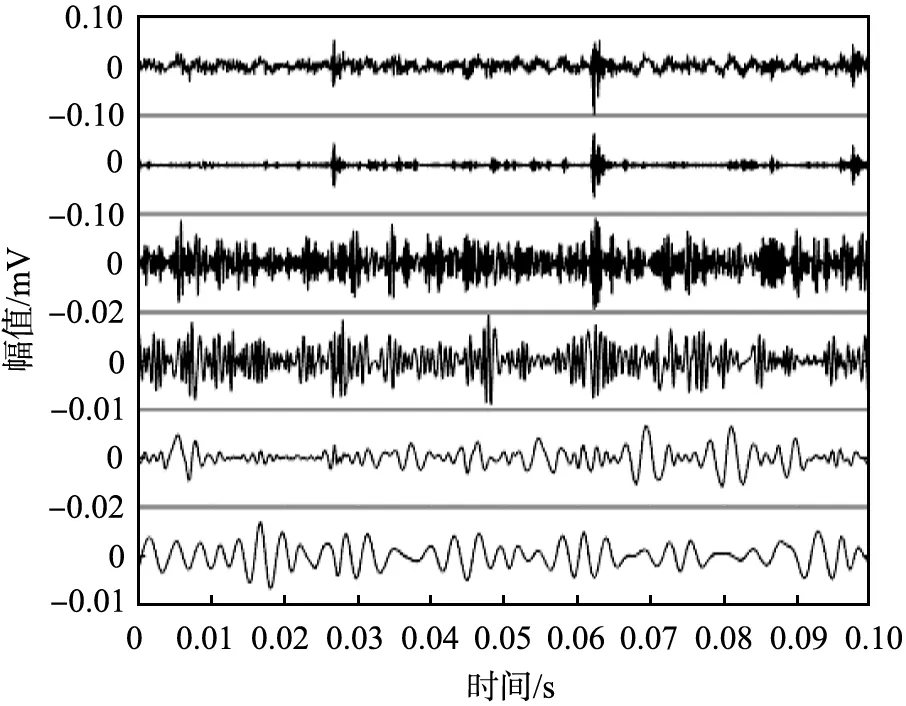
(a) 波形

(b) 频谱图7　集成经验模态分解各模态分量波形及频谱

6　结论

1)滚动轴承的故障振动信号为非平稳信号，采用VMD方法可以克服EEMD模态混叠的缺点，可以将复杂的非平稳信号分解为若干个平稳的IMFs，为后续的处理奠定了理论基础。

图8　集成经验模态分解结合粒子群优化支持向量机分类结果示意图

2)根据排列熵构造的特征向量可以作为SVM的有效输入，粒子群算法优化SVM参数提升了其分类性能。实验表明，VMD排列熵结合PSO-SVM方法可以准确判断轴承状态。