基于落锤装置的蜂窝铝夹芯结构动力学特性

　， ， 　， ，

蜂窝铝夹芯结构具有优异的力学、成型性能和成本优势，近年来在航空航天、船舶、交通运输、机械等领域中应用广泛[1-4]。蜂窝铝夹芯结构由上、下各层面板以及中间的蜂窝夹芯组成，中空的结构方式使其在空间占用方面具有较强的优势。蜂窝夹芯结构除了具有比刚度大、 比强度大以及耐压强的特点外， 还具有稳定的减震、 保温和良好的隔音、 阻燃性能。 蜂窝夹芯结构的芯子主要是纸、 金属、 高分子材料等， 在实际应用过程中， 一般承受多为冲击载荷的面外压力， 因此关于其动力学特性的研究尤为重要[5-15]。 鉴于此， 本文中利用落锤实验装置结合有限元仿真对蜂窝铝材料的动态力学性能进行分析。

1　实验及结果分析

为了保证实验的有效性，每种试样均准备3个。实验中使用的蜂窝铝夹芯结构所用材料为3003型铝合金，整体外观尺寸为60 mm×60 mm×20 mm(长度×宽度×高度)，其中蜂窝芯子高度为18.4 mm，上、下面板厚度均为0.8 mm，蜂窝胞元级别的规格为0.03 mm×2 mm(壁厚×边长)。

由表4可知，在相同负荷量和架空线型号的情况下，第④种配网拓扑模型即“负荷全部集中于10 kV中压线路的末端”时最大允许供电半径最小，即在该种情形下线路输送电能的能力最弱，认为是“木桶效应”中的“短板”，该短板将直接决定线路末端电压质量是否合格。因此，参考第④种配网拓扑模型下的最大允许供电半径进行中压架空线路的选型将不会出现中压线路末端低电压问题，这里将该供电半径定义为“合理供电半径”，不同线径及负荷下的合理供电半径具体情况如表5所示。

首先将蜂窝铝夹芯结构放置在底座的刚性平台上，然后安装导管。将落锤的后端设计成圆柱体的原因是圆形尾部平面可以直接连接在固定端的电磁铁上。实验开始时关闭电磁铁，落锤失去引力，脱离电磁铁，自由下落进入导管，沿着导管砸向试件上表面。根据实验设计要求，上、下调节固定端的高度，以此来控制落锤下落的速度。由于实验装置本身高度有限，因此落锤下落时所含势能势必受到限制。在此仅选择5、 10、 15 m/s这3种冲击速度，其他情况将在有限元仿真中进行讨论。当落锤的冲击速度分别为5、 10、 15 m/s时，蜂窝铝夹芯结构的凹痕深度分别为0.728、 1.263、 2.040 mm，凹陷面积如图1所示。由图可知，在受到落锤作用后，蜂窝铝夹芯结构的中心有不同程度的凹陷，且随着冲击速度的增大，凹陷逐渐加深，凹陷面积也逐渐加大。

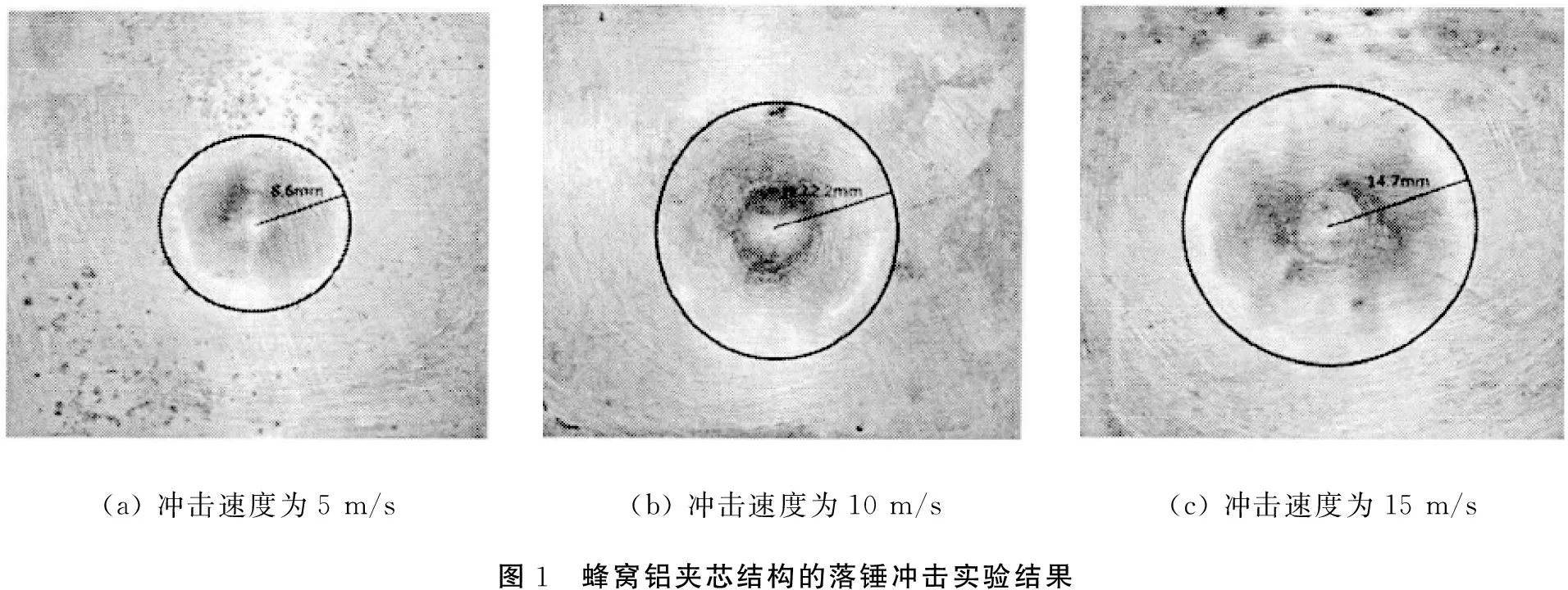
(a) 冲击速度为5 m/s(b) 冲击速度为10 m/s(c) 冲击速度为15 m/s图1 蜂窝铝夹芯结构的落锤冲击实验结果

2　数值计算及分析

利用ABAQUS有限元软件， 建立蜂窝铝夹芯结构落锤冲击实验仿真模型， 如图2所示。 有限元模型与实验实体模型尺寸比例为1∶1， 其中蜂窝铝夹芯结构采用三维可变形壳单元， 落锤采用三维可变形实体单元， 落锤和蜂窝铝夹芯结构的接触采用面-面接触方式， 接触对为蜂窝铝夹芯结构的上面板和落锤前端弧面。 对试件的面板施加相应的约束， 约束落锤刚体化并在预定义场中添加初速度。

2.1　仿真与实验结果对比

在仿真结果中，当落锤的冲击速度分别为5、 10、15 m/s时，蜂窝铝夹芯结构面板的凹痕深度如表1所示。由表可知，数值计算的凹痕深度比实验所得结果稍小， 原因是在建立数值计算模型时对冲击试验仿真模型进行了简化， 并且没有充分考虑蜂窝铝夹芯结构芯子以及芯子与面板连接处的缺陷，较为理想化；但是实际实验中很难避免此类缺陷，因此实验结果略大于数值计算结果。3种速度时蜂窝结构面板凹痕深度的误差均小于10%，可以认为数值计算方法是正确的。

(a)几何模型(b)网格划分模型图2 蜂窝夹芯结构的落锤冲击实验仿真模型

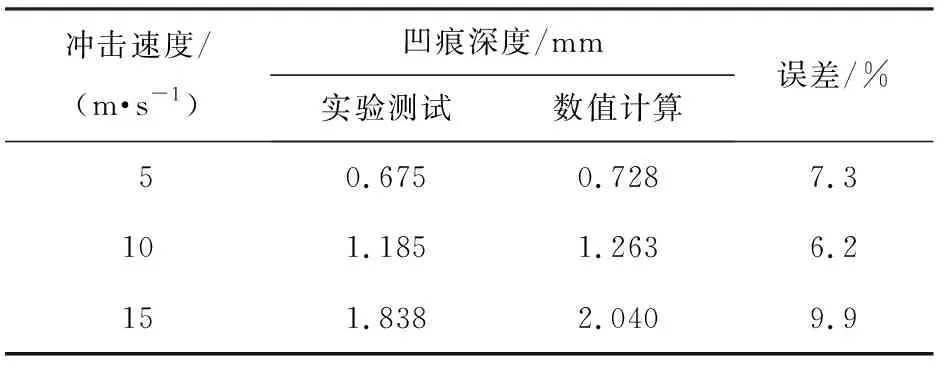
表1　蜂窝铝夹芯结构落锤冲击实验的有限元计算结果

2.2　分析与讨论

在落锤冲击实验过程中，当落锤速度分别为5、 20、 50 m/s时，蜂窝铝夹芯结构试件面板及其芯子各部位的应力分布如图3所示。由图可知，当落锤与面板接触后，面板中心处的应力开始集中，随着落锤凹痕深度的增大及其与面板接触面积的增大，应力以同心圆形向外层状发散，并且始终保持中心应力最大。当落锤凹痕深度达到最大时，面板的应力峰值及其扩散面积也达到最大，然后随着锤头的反弹，落锤锤头与面板脱离接触，应力幅值开始减小，应力扩散面积也相应减小，并且中心点不再是应力最大点。落锤冲击速度越大，在最大凹痕深度处的应力峰值和应力波辐射范围也越大。在落锤发生反弹而与面板脱离接触后，面板上的残余应力影响面积及幅值也越大。当应力的辐射范围足够大，直至与面板边缘相交时，应力不再以同心圆形状传播，开始异形发散。

(a)与落锤接触,冲击速度为5 m/s(b)位移最大,冲击速度为5 m/s(c)落锤离开后,冲击速度为5 m/s(d)与落锤接触,冲击速度为20 m/s(e)位移最大,冲击速度为20 m/s(f)落锤离开后,冲击速度为20 m/s(g)与落锤接触,冲击速度为50 m/s(h)位移最大,冲击速度为50 m/s(i)落锤离开后,冲击速度为50 m/s图3 不同冲击速度时蜂窝铝夹芯结构试件面板的应力分布

图4所示为蜂窝铝夹芯结构芯子在落锤冲击速度分别为5、 20、 50 m/s时各阶段的应力分布。 由图可知， 在受到落锤冲击后， 随着蜂窝铝夹芯结构面板发生变形， 与面板相连的蜂窝芯子也开始发生失稳， 在落锤下落位移最大时芯子变形量也达到最大， 并且应力峰值也最大。 应力沿着蜂窝芯子平面传播， 即图4中各图的左图所示， 而在垂直方向， 即图4中各图的右图所示， 在落锤刚与面板接触时， 受到面板的挤压， 蜂窝铝夹芯结构芯子发生变形， 开始出现应力， 并且不断向外扩张； 当落锤凹痕深度达到最大时， 应力传播范围达到最大， 并且应力峰值和在落锤开始发生反弹并与面板脱离接触后， 由于面板也会有所回弹， 因此芯子受到的压力减小， 应力峰值相应减小， 并且辐射范围也开始减小， 此时的应力峰值已经不再出现在中心地带。 落锤冲击速度越大， 蜂窝铝芯子在最大凹痕深度处的应力峰值和辐射范围也越大， 在落锤发生反弹与面板脱离接触后， 芯子中的残余应力影响面积及幅值也越大。

(a)冲击速度为5 m/s

(b)冲击速度为20 m/s

(c)冲击速度为50 m/s 图4　不同冲击速度时芯子在结构凹痕位移最大时和落锤离开后的应力分布

图5所示为不同冲击速度时蜂窝铝夹芯结构的落锤冲击凹痕深度和接触力。 由图5(a)可知， 随着冲击速度的增大， 蜂窝铝夹芯结构产生的凹痕深度也越大， 且呈线性增长。 由图5(b)可知， 蜂窝铝夹芯结构试件在受落锤冲击作用时的接触力变化过程可以分为3个阶段： 第1个阶段大致为整个作用时间段的前1/3， 此时落锤与试件面板建立接触， 并且蜂窝芯子处于弹性阶段， 因此接触力迅速增大； 第2个阶段大致为整个作用时间段的1/3～2/3， 此时落锤已经与面板建立了稳定的接触关系， 并且此时蜂窝芯子的变形开始进入塑性阶段，落锤受到的接触力增大幅度减小，接触力曲线较平缓；第3个阶段为整个作用时间段的后1/3，此时接触力开始急剧减小，原因是落锤开始反向运动，蜂窝芯子也开始缓慢恢复，但是因产生了塑性变形而恢复并不完全。

(a)凹痕深度(b)接触力图5 不同冲击速度v时蜂窝铝结构的落锤冲击凹痕深度和接触力

图6所示为落锤冲击速度为10 m/s时蜂窝铝夹芯结构的应变能与时间的关系。由图可知，该关系曲线分为3个阶段：第1个阶段为上升阶段，试件应变能不断增大，此阶段又可以细分为2个阶段，即芯子和面板均在弹性阶段，这时应变能也呈线性增长，当塑性变形发生时，应变能的增长不再呈线性变化(即图5(a)中达到峰值前的阶段)；第2个阶段为下降阶段，此时落锤开始反弹，蜂窝面板与芯子虽然发生了塑性变形，但是仍然有所反弹；第3个阶段为平台阶段，此时落锤与面板脱离，蜂窝铝夹芯结构也回到稳定状态。能量峰值为冲击总能量，平台阶段的能量值为蜂窝铝结构在落锤冲击过程中所吸收的能量，下降阶段的能量差值就是落锤反弹时的剩余能量。

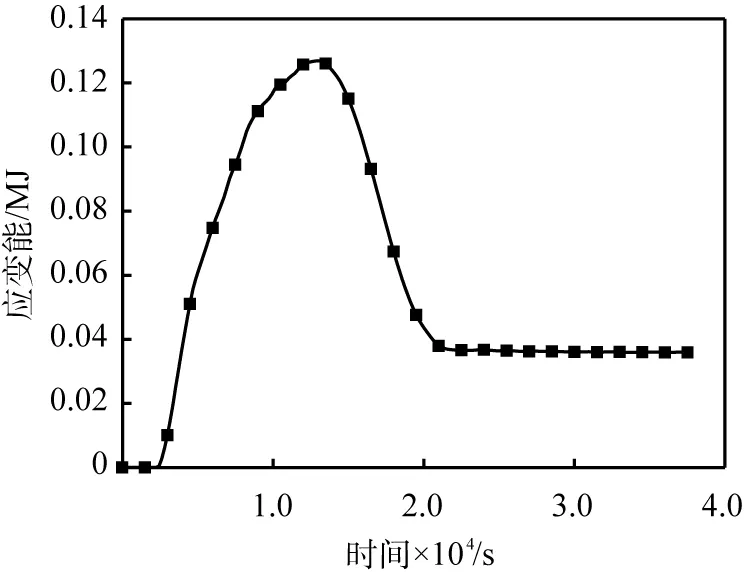
图6　冲击速度为10 m/s时蜂窝铝夹芯结构的应变能与时间的关系

图7所示为不同冲击速度时蜂窝铝夹芯结构吸收的能量与时间的关系。由图可知， 吸收能量随着速度的增大而增大，而吸收能量的幅值同时取决于势能的转化。

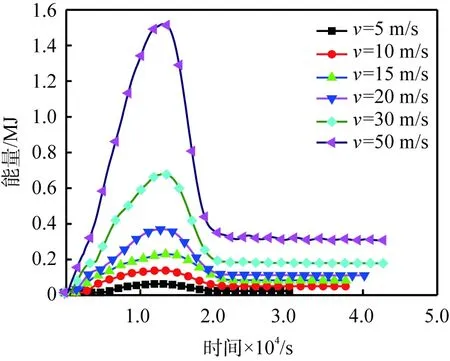
图7　不同冲击速度v时蜂窝铝夹芯结构吸收的能量与时间的关系

3　结论

本文中利用落锤装置对不同落锤速度造成的蜂窝铝夹芯结构面板上的凹痕深度进行了测试，建立了有限元模型，对落锤冲击过程的应力分布进行了分析，结论如下：

1)在落锤与试件接触时，蜂窝铝夹芯结构面板上的应力分布呈同心圆状向外发散，在圆心处的应力最大，当落锤开始反弹并与面板脱离时，应力幅值减小，但是影响面积只是小幅减小，且此时的应力最大点不在圆心处，而在围绕圆心附近的一个同心圆处。蜂窝铝夹芯结构芯子的应力呈异形向外发散，并在脱离接触后逐渐收缩。落锤冲击速度越大，面板和蜂窝芯子在最大凹痕深度处的应力峰值也越大，应力波辐射范围也越大。

2)在落锤下落过程中，接触力随时间的变化过程基本可以分为3个阶段：急速上升阶段，此时蜂窝铝夹芯结构芯子的变形尚在弹性阶段；载荷稳定阶段，此时蜂窝芯子面板开始发生塑性变形；载荷下降阶段，此时落锤开始发生回弹直至脱离接触。在落锤下落过程中，蜂窝铝夹芯结构吸收的能量随着落锤冲击速度的增大而相应增大，而吸收能量的幅值同时取决于势能的转化。

参考文献: