具有完全形式的边值问题解的存在唯一性

，

(山东科技大学 数学与系统科学学院， 山东 青岛 266590)

在材料力学中，具有完全形式的非线性(非线性项为连续函数)四阶两点边值问题描述了两端简单支撑的弹性梁在受力状态下的平衡方程。非线性项中未知函数的一阶导数、未知函数的二阶导数、未知函数的三阶导数分别表示梁的隅角、弯矩和剪力，因此具有完全形式的非线性四阶两点边值问题能全面、准确地反映弹性梁的受力状态。当非线性项中含有未知函数的一阶或二阶导数时，弹性梁问题的研究较为普遍[1-8]，所用的研究方法主要为先验估计和Leray-Schauder不动点定理。对于非线性项中含有未知函数的所有低阶导数时，弹性梁问题的研究较少[9-15]，主要原因是未知函数三阶导数的存在导致很难对具有完全形式的非线性四阶两点边值问题给出解的先验估计，从而弹性梁问题的研究有一定的理论难度，不易解决。

本文中假设非线性项在局部满足Lipschitz条件，利用降阶方法，将具有完全形式的非线性四阶两点边值问题转化为算子的不动点问题，利用压缩映射原理得到具有完全形式的非线性四阶两点边值问题解的存在唯一性结论。

1　预备知识

具有完全形式的非线性四阶两点边值问题为

(1)

式中：u(t)为未知函数；t为自变量；f[t,u(t),u′(t),u″(t),u‴(t)]为非线性项。

为了得到本文的主要结果，给出边值问题(1)的Green函数G(t,s)(其中s为积分变量，s∈[0,1])及其相关的性质和引理。

对于u(4)(t)=f[t,u(t),u′(t),u″(t),u‴(t)]，令φ(t)=f[t,u(t),u′(t),u″(t),u‴(t)]，边值问题(1)可化为

(2)

由文献[16]可知，边值问题(2)转为积分方程

(3)

其中

在积分方程(3)的两边求导可得

(4)

(5)

，

(6)

其中

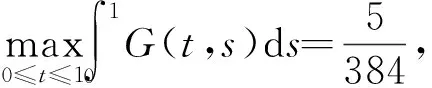
令u″(t)=v(t)，则边值问题(1)可转化为以下2个边值问题

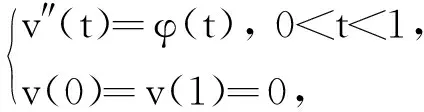
(7)

和

(8)

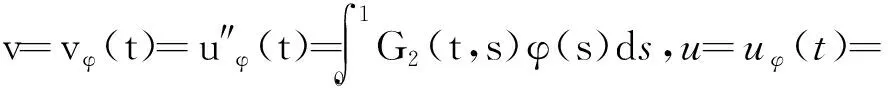
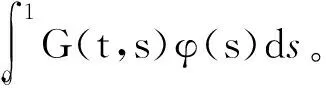
价于如下算子方程解的存在性，即

φ=Aφ

，

(9)

其中算子A∶C[0,1]→C[0,1]定义为

f[t,uφ(t),yφ(t),vφ(t),zφ(t)],

(10)

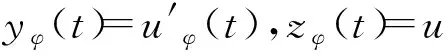
2　主要结论

引理1假设存在常数K>0;d1,d1,d2,d3≥0,使得函数f(t,u,y,v,z)在集合BK上满足

|f(t,u,y,v,z)|≤K

，

(11)

且对任意(t,u,y,v,z),(t,ui,yi,vi,zi)∈BK(i=1,2)有

|f(t,u1,y1,v1,z1)-f(t,u2,y2,v2,z2)|≤

d0|u2-u1|+d1|y2-y1|+d2|v2-v1|+d3|z2-z1|。

(12)

如果

(13)

则算子A是定义在集合B[O,K]上的压缩算子。

证明：任取φ∈B[O,K]，则式(10)中的uφ(t)、yφ(t)、vφ(t)、zφ(t)满足

从而当φ∈B[O,K]，有

这说明算子A是定义在集合B[O,K]上的映射。再由式(11)可知，A为B[O,K]到其自身的映射。

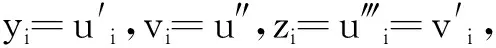
根据式(10)、(12)有

|(Aφ2)(t)-(Aφ1)(t)|=

|f[t,u2(t),y2(t),v2(t),z2(t)]-

f[t,u1(t),y1(t),v1(t),z1(t)]|≤

d0|u2(t)-u1(t)|+d1|y2(t)-y1(t)|+

d2|v2(t)-v1(t)|+d3|z2(t)-z1(t)|。

由此可知，当式(13)成立时，算子A是定义在B[O,K]上的压缩算子。证毕。

定理1在引理1的假设下，边值问题(1)存在满足以下估计的唯一解，

(14)

证明:要证明边值问题(1)有唯一解，只须说明边值问题(7)、(8)有唯一解即可，而边值问题(7)、(8)有唯一解只须算子A在集合B[O,K]中有唯一不动点。由引理1可知，算子A为B[O,K]到其自身的压缩算子，因此由压缩映射原理可知，算子A在B[O,K]中有唯一不动点，进而边值问题(1)存在满足条件的唯一解。证毕。

在实际的弹性梁问题中，只有正解的存在性才有意义，下面考虑边值问题(1)正解的存在唯一性。

令

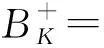
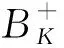
0≤f(t,u,y,v,z)≤K

,

(15)

0≤(Aφ)(t)≤K，t∈[0,1]。

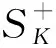
由压缩原理可知，边值问题(1)的解可由迭代得到。特别取φ0(t)=f(t,0,0,0,0)，作如下迭代:

φk+1=f[t,uφk(t),yφk(t),vφk(t),zφk(t)]，k=0,1,2,…。

(16)

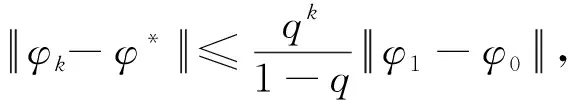
其中φ0为算子方程(9)在B[O,K]上的唯一解，从

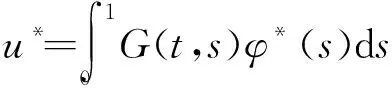
特别地，当f不依赖于u′和u‴时，迭代序列相对于初始函数是单调的，即当边值问题(1)退化为

(17)

时，可得定理3。

证明:根据式(7)、(8)有

其中

从而

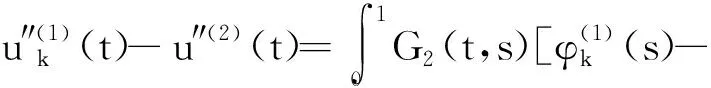
t∈[0,1]，k=1,2,…，(18)

t∈[0,1]，k=1,2,…。(19)

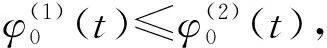
注：定理3中的函数g在有界闭集DK上而非[0,1]×2上满足一定的条件, 因而初始值函数可取

3　总结

本文中利用降阶方法， 将具有完全形式的四阶两点边值问题解的存在唯一性问题转化为算子不动点的存在唯一性问题。 非线性项在局部满足Lipschitz条件下， 利用压缩映像原理得到了四阶两点边值问题解的存在唯一性。 在物理学、 力学等领域中， 本文中的结论具有重要的价值。在今后的研究工作中， 可以考虑应用全局分歧理论研究解的存在性或者利用不动点理论来研究非线性项满足Nagumo条件下正解的存在性。