基于脉冲算法的多智能体系统编队牵制控制
,
(太原理工大学 a. 数学学院, b. 大数据学院, 山西 太原 030024)
近几年,多智能体系统的协同控制在植绒、同步、牵制及编队控制等各方面的潜在应用吸引了大量学者的科学研究。系统协同控制的典型研究包括一致性、牵制控制及编队控制等。基于牵制控制和编队控制,出现了更复杂的编队牵制控制问题,即要求领导者的状态实现理想的编队控制, 同时跟随者的状态收敛到领导者形成的凸包。学者们研究了各种无向或有向拓扑结构下的一阶、二阶系统的编队牵制问题[1-4]。编队、牵制控制、一致性和一致追踪问题都可以作为编队牵制控制问题的特殊情形。
当前,脉冲控制方法已经被证明在混沌系统、混杂系统及复杂网络的同步应用中是有效且有鲁棒性的[5-7]。将脉冲控制方法应用到多智能体系统的一致性问题中有诸多优点,如结构简单、快速瞬态以及低成本等。对于给定的多智能体系统,如何结合脉冲控制的优点设计相应的脉冲控制协议,从而使得整个系统达到一致是一个值得研究的问题。文献[8]中基于智能体局部信息的脉冲控制协议,研究了一类非线性动态系统的同步问题。文献[9]中基于分布式脉冲一致算法,研究了一阶积分器多智能体系统,并得出采用脉冲算法控制收敛更快的结论。文献[10]中研究了一类切换拓扑结构下二阶积分器多智能体系统的脉冲一致性问题。文献[11]中研究了有向动态网络结构下,基于采样信息的二阶多智能体系统,采用脉冲控制算法使其速度和位移状态都实现了一致性。
许多智能体之间的信息传递可能是间歇的而不是持续性的,由于脉冲控制器在采样时刻起作用,因此智能体之间采用脉冲控制器就是实用且有效的。例如,在多智能体系统中,在瞬时向多个智能体发送一个脉冲可以减少不必要信息的同时传送信号,并且可以改善智能体干扰的鲁棒性。由此可以想到,采用脉冲一致性算法实现多智能体系统的编队控制应该有好的效果,即通过设计脉冲算法去实现多智能体系统的编队牵制控制。
本文中为了研究有向拓扑结构条件下的高阶线性多智能体系统的编队牵制问题,对领导者和跟随者分别提出2种控制协议,以确保领导者在脉冲算法的作用下实现理想的时变编队控制,同时跟随者实现牵制控制,即领导者的状态在脉冲算法的作用下应实现设定好的编队控制,同时跟随者的状态被牵制到领导者生成的凸包,其中拓扑结构是有向的,并且领导者分别在同步脉冲、不活跃脉冲及失步脉冲作用下实现编队控制;将编队牵制控制问题转化为渐近稳定性问题,并提出实现编队牵制控制的充分条件;通过仿真实例验证所得结果的有效性。
1 预备知识
1.1 图论知识
设G(V,E,W)是一个图,其中V={1,2,…,n}是所有节点的集合,E⊆V×V是所有边的集合,W=(wij)是邻接矩阵,i,j=0,1,2,…。如果存在一条边从Vi(第i个节点)到Vj,即(Vi,Vj)∈E,那么wij>0,否则wij=0,并且W的对角线元素都为0,即wii=0。图G的度矩阵表示为D=diag(di),i=0,1,2,…。图G的拉普拉斯矩阵表示为L=D-A=(lij)∈且lij=-wij对任意的i≠j都成立。
引理1[12]设L∈n×n是一个有向图G的拉普拉斯矩阵。如果G有一个生成树,那么L有且仅有一个零特征值且IN是对应的特征向量,其他N-1个特征值均有正实部。
1.2 问题描述
本文中考虑有N个节点的多智能体系统。假设系统里有M个跟随者和N-M个领导者。分别用F={1,2,…,M}和L={M+1,M+2,…,N}表示跟随者和领导者的集合。如果一个节点不能从其他节点接收信息,称这个节点是一个领导者;否则,称这个节点是一个跟随者。图G(V,E,W)表示节点之间的拓扑。多智能体系统的动态描述为
(1)
式中:t为运动时间;xi(t)∈n和ui(t)∈m分别为第i个节点的状态和输入控制,n和m均为向量维数;A和B为常数矩阵。
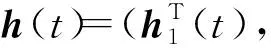
(2)
成立。
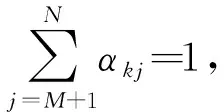
(3)
成立。
定义3[13]称系统(1)实现编队牵制控制,如果对任意给定的有界初始状态及任意i∈L及k∈F,存在一个向量值函数r(t)∈n和非负常数αkj满足使得式(2)、(3)同时成立。
定义4[14]平均脉冲间隔脉冲序列ζ={t1,t2,…} 的平均脉冲间隔为T0,如果存在正整数N0和正数T0,使得
(4)
式中:T为任意时间点;∀0≤t≤T,Nζ(T,t)为脉冲序列ζ在间隔(t,T)上的脉冲次数。
假设1有向图G中,对于每个跟随者都存在一条由至少一个领导者指向它的路径。
G1为领导者之间的拓扑关系。假设G1有一个生成树。基于领导者和跟随者的性质,图G的拉普拉斯矩阵可以分解为
式中:L1∈M×M为跟随者的拉普拉斯矩阵;L2∈M×(N-M)为领导者和跟随者之间的信息拓扑;L3∈(N-M)×(N-M)为领导者的拉普拉斯矩阵。
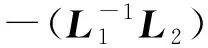
引理3[16]对任意合适维数的矩阵P、Q、C和D, Kronecker积有下列的性质:
1)(cP)⊗Q=P⊗(cQ),其中c为常数,⊗为Kronecker积运算;
2)(P+Q)⊗C=P⊗C+Q⊗C;
3)(P⊗Q)(C⊗D)=(PC)⊗(QD);
4)(P⊗Q)T=PT⊗QT。
2 带脉冲算法的编队牵制控制
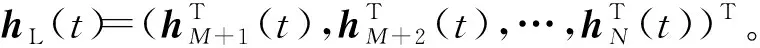
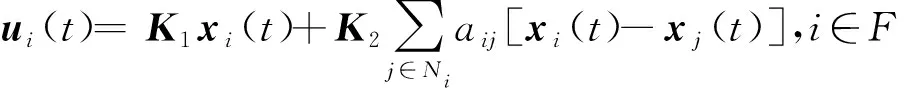
(5)
领导者的控制输入为

hj(t)]},i∈L,t≠tk,
(6)
(7)
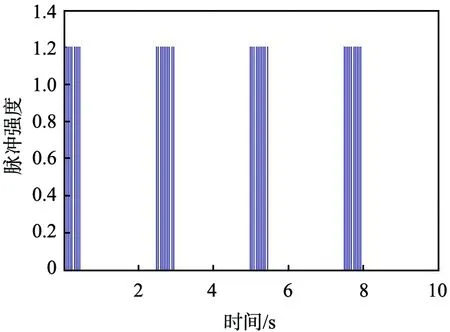
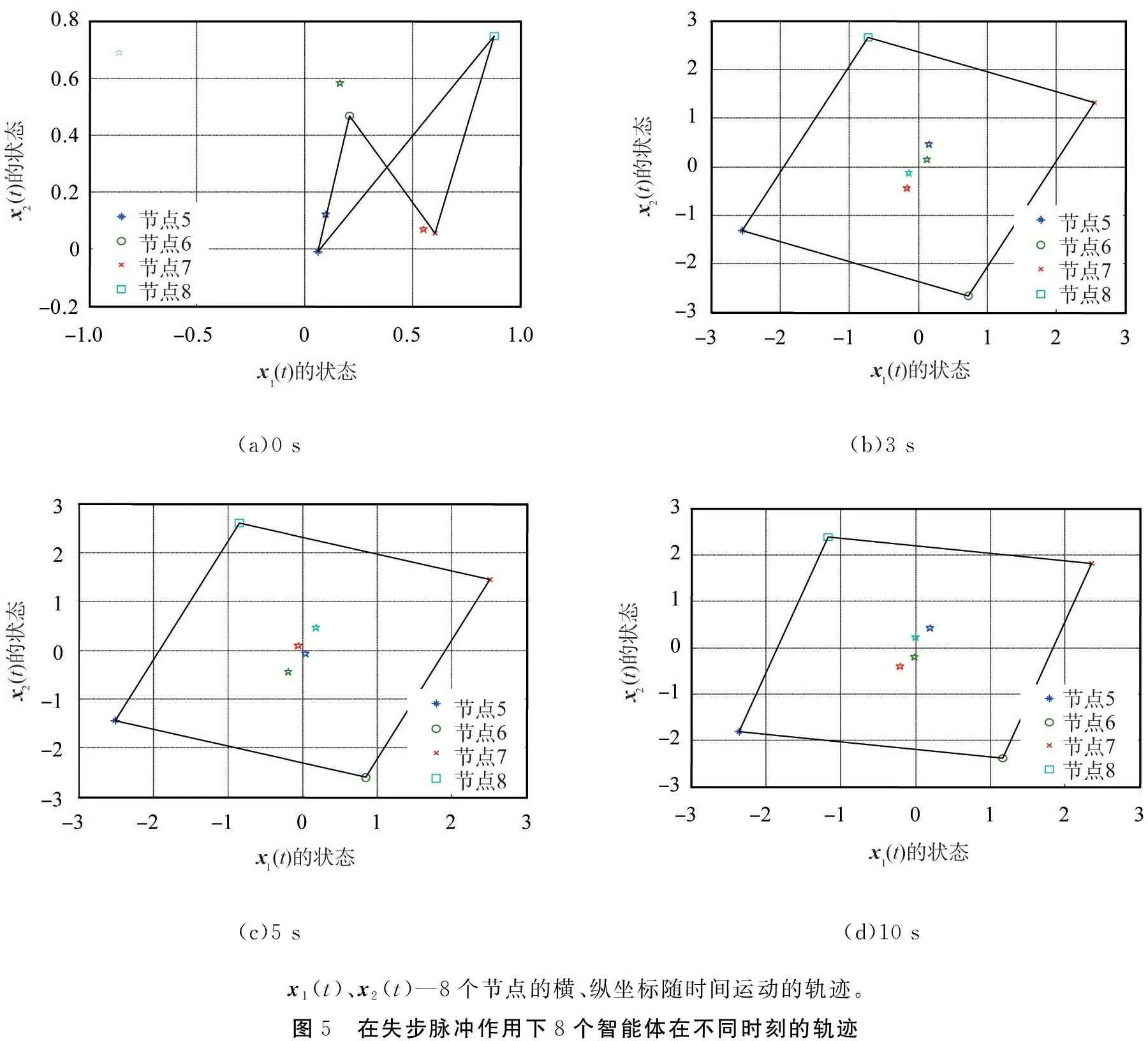
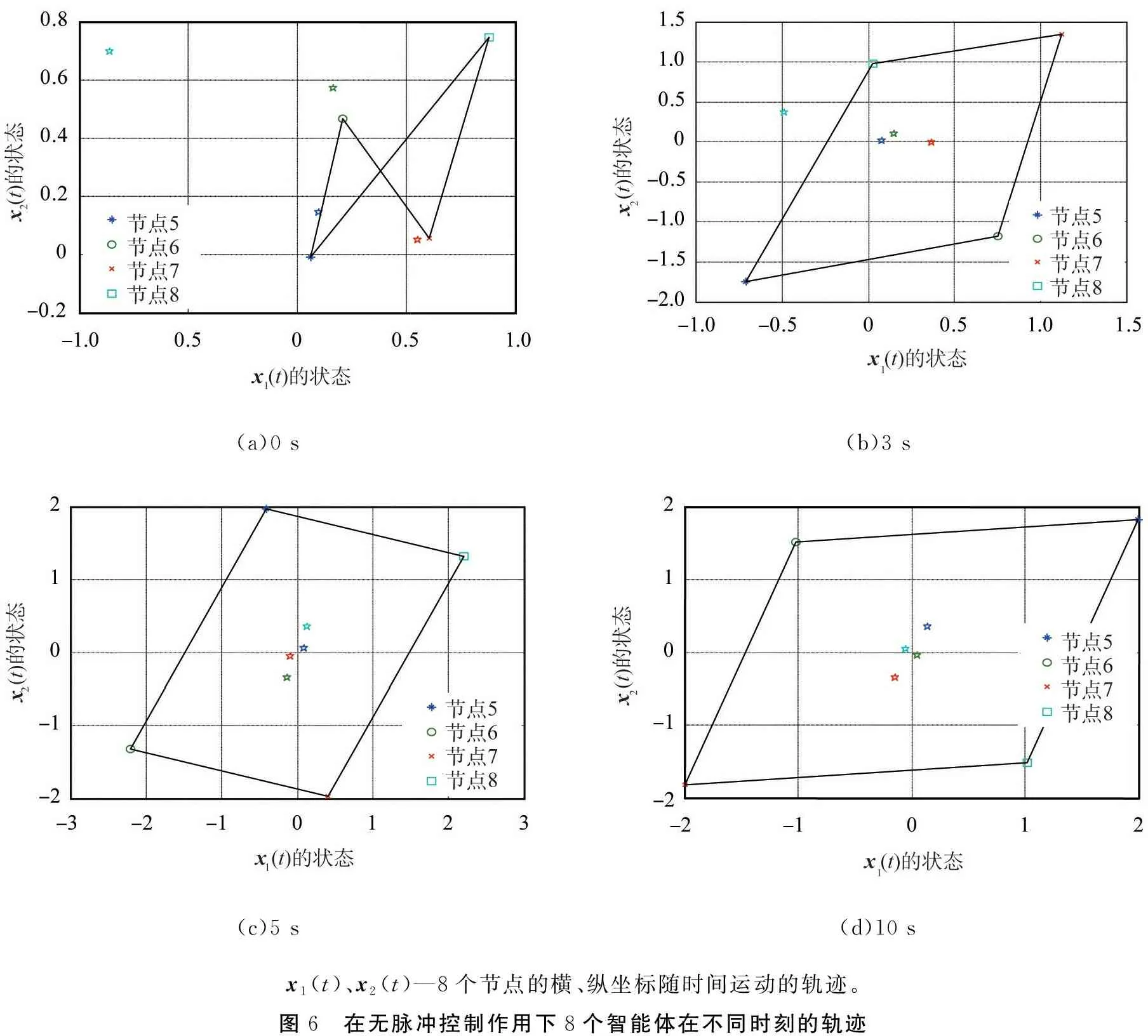
式中:Ki∈m×n(i=1, 2, 3)为常数增益矩阵;μ为脉冲信号的强度;tk为脉冲时刻,k=1,2,…,且脉冲时刻序列满足 0=t0 , (8) (L3⊗BK3)hL(t),t≠tk。 (9) i∈L,t≠tk, (10) (11) 脉冲算法(11)可改写为Kronecker积形式,即 。 (12) (13) t≠tk。 (14) 为了实现系统(1)的牵制控制,令 (15) θ(t)=-(L1⊗I)xf(t)-(L2⊗I)xL(t) , (16) 如果θ(t)→0,可得 。 (17) 根据式(17)、引理2和定义2可得,系统(1)将实现牵制控制。 定理1系统(1)在控制协议(5)、(6)、 (7)作用下实现编队牵制控制,如果下列不等式同时成立: 1)对任意i,j∈L, (18) 2)对任意i∈L, 2ln|μ|+αT0<0 , (19) 3)对任意i∈F,A+BK1-λiBK2是Hurwitz的。 证明:如果条件1)成立,则有 (20) (21) (22) 考虑下列子系统的稳定性: (23) 由(14)式和条件(23)化简得 (24) 如果系统(23)渐近稳定,则可得系统(24)也是渐近稳定的。考虑Lyapunov函数 (25) 当t∈(tk-1,tk],k∈+, 沿着系统(25)的轨迹对V(t)求导可得 αV(t),i=M+2,M+3,…,N, (26) 由此可得 (27) 其中t∈(tk-1,tk],k∈+。当t=tk,k∈+,有 (28) 根据式(27)、(28),有以下结论: (29) 下面分别考虑同步脉冲(0<|μ|<1),不活跃脉冲(|μ|=1)和失步脉冲(|μ|>0)。由于脉冲序列ζ={t1,t2,…}的平均脉冲间隔为T0,因此有 (30) 如果0<|μ|<1,由式(29)、(30)可得 (31) 当|μ|=1,有μ2k=1。由式(29)可得 (32) 类似地,当|μ|>1,由式(29)、(30)可得 (33) 结合不等式(31)、(32)、(33),给定常数M0=max{μ-2N0,1,μ2N0},则有 (34) 如果条件2)成立, 那么由式(24)描述的N-M-1维子系统是渐近稳定的,即 (35) 由引理5和式(35)知, 系统(9)实现了时变编队hL(t)。 当领导者实现时变编队h1(t)时,则有 (36) 由于L31=0,因此 。 (37) 由式(8)、(9)、(16)可得 (L2L3⊗BK3)[xL(t)-hL(t)]。 (38) 由式(37)和(38)可得 (39) 根据L1的结构,考虑子系统 (40) 如果条件3)成立,那么子系统(40)是渐近稳定的,进而系统(39)是渐近稳定的。 由式(37)、(48)、(49)可得 (41) 再由式(35)、(41),可证系统(1)在控制输入(5)、(6)和脉冲算法(7)的作用下实现了编队牵制控制。 定理1得证。 推论1在M=0的情况下,系统(1) 在控制协议(6)、(7)的作用下实现编队hL(t),如果定理1中的条件1)和2)成立。 推论2在领导者没有邻居且不加脉冲控制的情况下,系统(1)在控制协议(5)、(6)的作用下实现牵制控制,如果定理1中的条件3)成立。 假设在这个系统中有4个领导者和4个跟随者。图1所示为系统的拓扑结构。为了简便,假设节点之间相互作用的权重为0~1。 节点1—4为跟随者;节点5—8为领导者。图1 有向图G的拓扑结构 系统的编队牵制问题描述如下。首先,4个领导者要实现一个时变的平行四边形并围绕提前设定好的时变编队参考函数保持运动。编队定义为 其次,要求4个跟随者收敛到由4个领导者的状态形成的凸包。 选择K1=(-4,-5)赋值求A+BK1的特征值。这种情况下,编队函数将进行周期性运动。可以验证满足定理1中的条件1)成立且(A,B)是可稳定的,因此,为了确保系统(1)实现编队牵制控制,选取矩阵K2=(-0.9,0.4)和K3=(-1.9,0.9)。 为了描述简单,系统状态表示为(x1(t),x2(t))T,其中x1(t)=(xi1(t))T,x2(t)=(xi2(t))T,i=1,2,…,8表示8个节点。 给出脉冲序列ζ={ε,2ε,…,(N0-1)ε,N0T0,N0T0+ε,N0T0+2ε,…,N0T0+(N0-1)ε,2N0t0,…}, 根据定理1中的条件2), 首先考虑同步脉冲作用下系统的编队牵制控制, 令脉冲信号强度μ=0.8,则可选取平均脉冲间隔T0=0.12,N0=10,ε=0.05,则可得同步脉冲序列,如图2所示。此时领导者可以实现编队控制,同时跟随者也收敛到领导者形成的凸包,如图3所示,其中领导者的状态轨迹由智能体5—8表示,跟随者由4个不同颜色的五角星表示。此外,领导者的状态形成的凸包用实线标记。图3(a)—(c)所示为同步脉冲作用下领导者实现了理想的平行四边形编队,同时跟随者的状态也收敛到领导者状态形成的凸包。图3(b)—(d)所示为已实现的编队保持时变运动。 图2 同步脉冲序列 (a)0 s(b)3 s(c)5 s(d)10 sx1(t)、 x2(t)—8个节点的横、纵坐标随时间运动的轨迹。图3 在同步脉冲作用下8个智能体在不同时刻的轨迹 考虑失步脉冲作用下系统的编队牵制控制,令脉冲信号强度μ=1.2,则可选取平均脉冲间隔T0=0.12,N0=10,ε=0.05,得失步脉冲序列,如图4所示。此时领导者可以实现编队控制,同时跟随者也收敛到领导者形成的凸包,如图5所示,其中领导者的状态轨迹由智能体5—8表示,跟随者由4个不同 图4 失步脉冲序列 颜色的五角星表示。此外,领导者的状态形成的凸包用实线标记。图5(a)—(c)所示为失步脉冲作用下领导者实现了理想的平行四边形编队,同时跟随者的状态也收敛到领导者状态形成的凸包。图5(b)—(d)所示为已实现的编队继续保持时变运动。 同时,仿真中也考虑多智能体系统无脉冲输入控制时的情况,取同样的K1、K2、K3,系统(1)也可以实现编队牵制控制,如图6所示,其中领导者的状态轨迹由智能体5—8表示,跟随者由4个不同颜色的五角星表示。 此外, 领导者的状态形成的凸包用实线标记。图6(a)—(c)所示为无脉冲作用下领导者实现了理想的平行四边形编队,同时跟随者的状态也收敛到领导者状态形成的凸包。图6(b)—(d)所示为已实现的编队保持时变运动。通过与图3、5相比较可知,对于同一多智能体系统,基于脉冲一致算法实现的编队牵制控制速度更快。 (a)0 s(b)3 s(c)5 s(d)10 sx1(t)、x2(t)—8个节点的横、纵坐标随时间运动的轨迹。图5 在失步脉冲作用下8个智能体在不同时刻的轨迹 (a)0 s(b)3 s(c)5 s(d)10 sx1(t)、x2(t)—8个节点的横、纵坐标随时间运动的轨迹。图6 在无脉冲控制作用下8个智能体在不同时刻的轨迹 本文中研究了多智能体系统基于脉冲算法的编队牵制控制问题。分别针对领导者和跟随者提出不同的控制协议,且领导者的状态实现了预定的时变编队,同时跟随者的状态收敛到领导者形成的凸包。将编队牵制控制问题转化为渐近稳定性问题,并对多智能体系统在脉冲算法的作用下实现编队牵制控制提出了充分条件。牵制问题、编队控制问题都可以作为编队牵制问题的特殊情形。今后的研究方向是针对时变无向或时变有向拓扑结构的多智能体系统,在脉冲算法的作用下实现编队牵制控制。
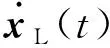
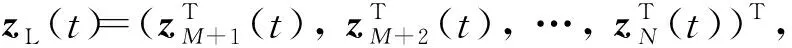
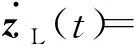
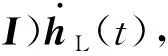
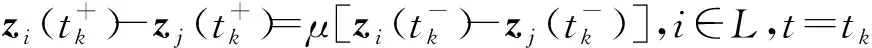

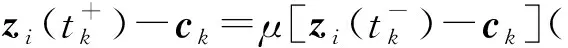



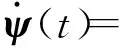
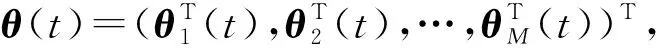
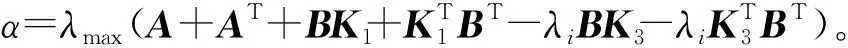
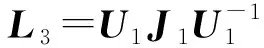

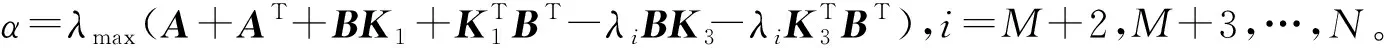


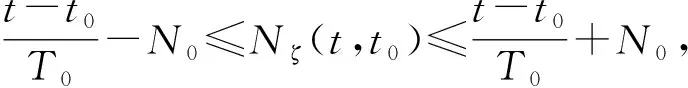
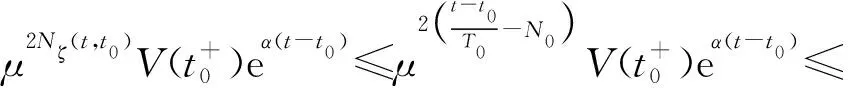
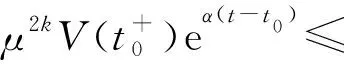
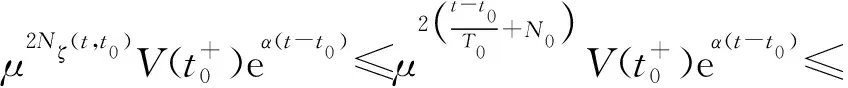

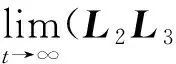
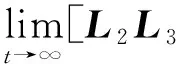
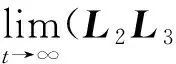
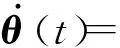
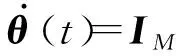
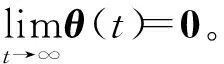
3 数值仿真
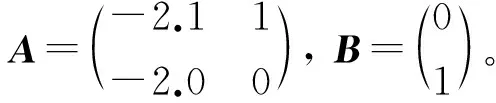



4 结论
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

