Mm,n(R)中具有Schm idt数的某个固定数R的纠缠基的讨论
乔世东
(山西大同大学数学与计算机科学学院,山西大同037009)
纠缠是量子力学现象中的突出特征之一,随着物理学的发展,一直与数学的发展密不可分,用数学理论解决物理问题已有几百年的历史,近二十多年来,以矩阵和算子理论作为重要数学工具的量子信息科学发展极快。首先从数学上给出纠缠的定义,但刻画纠缠性也是一个数学难题,在有限维情形,纠缠刻画问题可化为矩阵代数的问题。
设Mm,n(R )表示全体m×n实矩阵空间,m≤n,若满足如下条件,则称为
Mm,n(R)中的一组Schmidt数为k的纠缠基[1]。
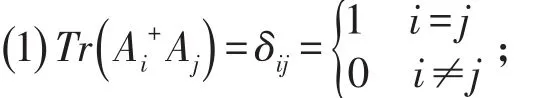
(2) rank(Ai)≤k,i=1,2,…,m,n,其中 k为某个正整数,1≤k≤min{m ,n};
(3) Ai的非零齐异值[2]为
且平方和等于1。
定义1矩阵A的奇异值为AA+或AA+的本征值的非负平方根。
定义2Tr(A)为A的全体特征值的和。
结果
(Ⅰ)当m=n=2,k=2时,


当


所以矩阵中的一组Schmidt数为 k的纠缠基的条件为(3),(4),(5),(6)成立。当i=j时,由条件(1)知,

由条件(5)知,
由条件(6)知,

由(7)知,a21=±a12, (9)例如:

当或

所以矩阵中的一组Schmidt数为 k的纠缠基的条件为(10),(11),(12),(13)成立。

由条件(12)知,

由(14)知,a13=±a22, (16)
同理当a12=a22=0时,
a11=±a13,a23=±a21。
当a13=a23=0时,a11=±a12,a22=±a21。
例如:




当的特征值为,

所以矩阵为M(R)中的一组Schmidtm,n数为k的纠缠基的条件为(7)~(13)成立。

[1]王晓红,费少明.量子纠缠与可分性[M].北京:清华大学出版社,2007.
[2]程云鹏,张凯院,徐仲,等,矩阵论[M].西安:西北工业大学出版社,2008:5.

