带投资回报的一类期望折现罚金函数
邵晶晶,王秀莲∗
(天津师范大学数学科学学院,天津300387)
1988年,Hans U Gerber等[1]研究了经典风险模型下的期望折现罚金函数。关于索赔时间间隔服从相位分布的情况,Zhimin Zhang等[2]研究了两种索赔的期望折现罚金函数;同时,Min Song等[3]研究了一种索赔的期望折现罚金函数;在带干扰的模型下,Shan Shan Wang 等[4]和 Wuyuan Jiang等[5]分别研究了一种和两种索赔的最大剩余;Lanpeng Ji等[6]研究了两种更新过程的期望折现罚金函数;Hu Yang等[7]在离散风险模型下研究了两种跳跃方式的期望折现罚金函数;卓文焱等[8]研究了在随机回报模型下的期望折现罚金函数。学者们根据不同研究问题,选择不同的罚金函数,如:Hansjörg Albrecher等[9]选取了罚金函数取为指数形式;Hans U Gerber等[10]选取了罚金函数为w(U(T))。是在随机回报下考虑索赔时间间隔为相位分布且有两种跳跃方式的期望折现罚金函数。
1 模型建立
考虑完备概率空间(Ω,ℱ,P)上Sparre Andersen风险盈余过程{C (t),t≥0},

其中u是初始资产,c是单位时间内收取的保费;{N (t),t≥0}表示到t时刻索赔和盈利发生的总数,N(t)=sup{n :V1+V2+…+Vn≤t}(s u p{∅ }=0),
其中时间间隔Vi是独立同分布的正值Vi~V随机变量,它们有共同的密度函数 fV(x)且期望为μV。{Xi,i=1,2,…} 是独立同分布的非零随机变量,Xi~X有密度函数 f(x)且期望为 μ。假设X有正数和负数值集,其中正数表示索赔额,负数表示保险公司的随机盈利。最后,假设{Xi}和{Vi}相互独立。
假设投资回报过程为Rt=δt,其中δ≥0为常数,则t时刻保险公司的盈余过程为:

假设时间间隔V有相应的状态空间E={0 ,1,2,…,M},其中1,2,…,M是转移态,0是吸收态。索赔时间间隔随机变量Vi的分布 fV(x)是相位分布,其中且是 n×n矩阵,且a)T有为长度为 n 的列向量且所有元素都是1,有
对于密度函数 f(x)可通过下面的形式表示:
其中0<p+,p-<1,p++p-=1,f+,f-是两个定义在ℕ+上的密度函数且I(·)为示性函数。在这里,f+和 f-分别代表索赔额和随机盈利的密度函数。实际上,“+”表示X是正的,相反的,“-”表示X是负的。
2 积分微分方程满足的积分-微分方程
在给定初始马氏态J0=i(i = 1,2,…,M),根据定义:ϕi(u)=

(其中 τ=inf{t : C(t)<0} 是破产时间,有 τ=∞,若C(t)≥0,∀t∈ℕ。期初盈余u的破产概率可定义为其中
在短时间(0 ,t]内,根据首次状态发生变化和首次跳跃发生的时刻进行讨论,有以下四种情况:
①在(0 ,t]区间内既没有发生状态改变也没有发生跳跃;
②在(0 ,t]区间内发生了状态改变但没有发生跳跃;
③在(0 ,t]区间内发生了跳跃但没有发生状态改变;
④在(0 ,t]区间内既发生了跳跃又有发生状态改变。
令若在 (0 ,t]区间内没有发生跳跃,则有C(t)=u+h(t)。由马氏性有,
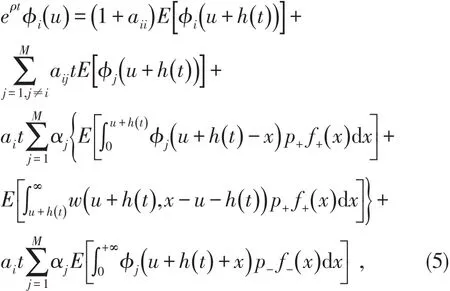
故(5)式可化为


其中根据泰勒展开有:
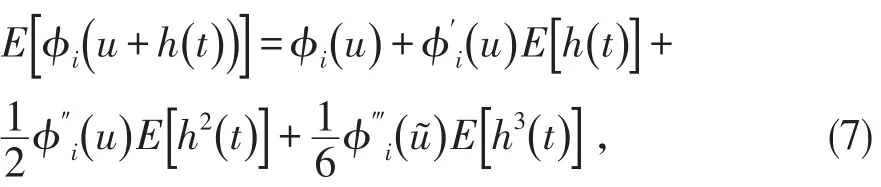
其中u≤
利用文献[8]中引理1的结论有:

上式关于t求导得:

在式(8)和式(9)中令t→0,并利用文献[5]中附录的结论有:


对于式(6)关于t求导得:令t→0并将(10)和(11)带入(12),整理可得:其中




I=diag(1 , 1,…,1),其中取定w(u ,x-u)=1,0⇀表示一个长度为n的列向量,所有元素均为0。当时,破产不会发生,故有故有
3显式表达式
对f-(x)=λe-λx,其中 λ 为指数参数。对等式(14)两边作Laplace变换,得到方程:
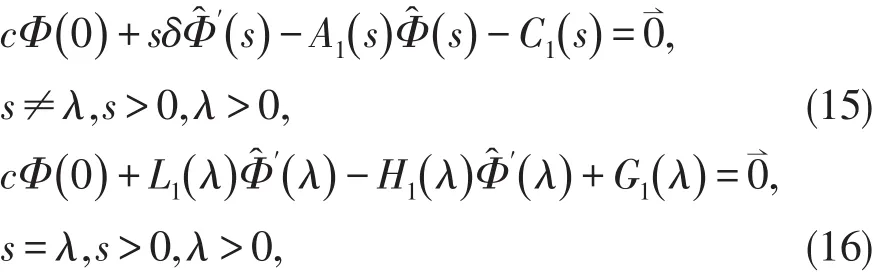
其中

此时将λ看作变量,通过求解微分方程通解公式,可解(16)式有:

其中

对(17)式做Laplace逆变换可得出:

其中的Laplace逆变换。
接下来,当1不是(u )的特征函数时,将(18)式中的u=0,可得到Φ(0)的值:

将(19)式带入(17)可得的值为:

通过求解微分方程通解公式,可解(15)式有:

将(19)式和(20)式带入(21)式就得到了s≠λ的表达式,故有:

对(22)做Laplace逆变换就得到了Φ(u)的表达式。
4结论
研究了在时间间隔为相位分布的情况下,两种跳跃方式的连续时间投资回报更新过程。考虑其中破产率函数恒为1时的情况,通过得到积分微分方程,找到合适的方法,进一步计算,得到该模型下的期望折现罚金函数,在以后的那就中,我们可以考虑破产函数和向上跳跃服从的分布更加复杂的情况。
[1]HANS U,GERBER,ELIAS S W.On the time value of ruin[J].North American Actuarial Journal,1998,2(1):48-72.
[2]ZHANG ZHIMIN,LI SHUANMING,YANG HU.The Gerber-Shiu discounted penalty functions for a risk model with two classes of claims[J].Journal of Computational&Applied Mathematics,2009,230(2):643-655.
[3]SONG MIN,MENG QINGBIN,WU RONG,eatl.The Gerber-Shiu discounted penalty function in the risk process with phase-type interclaim times[J].Applied Mathematics&Computation,2010,216(2):523-531.
[4]WANG SHAN SHAN,ZHANG CHUN SHENG.The Maximum Surplus before Ruin and Related Problems in a Jump-Diffusion Re⁃newal Risk Process[J].数学学报(英文版),2011,27(12):2379-2394.
[5]JIANG WUYUAN,MA CHAOQUN.The maximum surplus before ruin for two classes of perturbed risk model[J].Applicable Analy⁃sis,2017:124-133.
[6]JI LANPENG,ZHANG CHUNSHENG.The Gerber-Shiu penalty functions for two classes of renewal risk processes[J].Journal of Computational&Applied Mathematics,2010,233(10):2575-2589.
[7]YANG HU,ZHANG ZHIMIN.On a discrete risk model with two-sided jumps[J].Journal of Computational&Applied Mathematics,2010,234(3):835-844.
[8]卓文焱,封林云,陈旭.随机观察和随机回报的扩散风险模型中的Gerber-Shiu函数研究[J].统计与决策,2014(23):7-11.
[9]HANSJÖRG ALBRECHER,CHEUNG C K,THONHAUSER S.Randomized observation periods for the compound Possion risk mod⁃el:the discounted penalty function[J].Scandinavian Actuarial Journal,2013(6):424-452.
[10]HANS U GERBER,SHIU ELIAS S W,YANG HAILIANG.The Omega model:from bankruptcy to occupation time in the red[J].European Actuarial Journal,2012,2(2):259-272.

