基于声固耦合法的双体船水下近场噪声特性研究

宋 旭，高晟耀，于博天，田宏业

（1.中国船级社，北京 100007； 2.哈尔滨工程大学，哈尔滨 150001；3.中国人民解放军92537部队，北京 100161； 4.黑龙江省经济管理干部学院，哈尔滨 150001）

近年来，双体船技术愈加成熟。在科考船、测量船等领域，双体船由于其阻力小、稳性好、甲板面积大、易于使用等优点得到了更为广泛的应用。双体船由于存在两侧潜体，一方面将影响其内部布置形式，另一方面将改变其结构辐射特性，其水下近场噪声特性与单体船舶可能存在较大差异。在进行科学活动、测量等作业时，水下近场噪声可能会对作业产生影响，因此从声学设计及低噪声使用等方面考虑，开展双体船水下近场噪声特性研究、探索其与单体船舶的差异具有工程意义。

目前主流的船舶水下噪声预报方法主要有以下方法 ：即统计能量法[1–2]、有限元法[3–5]、边界元法[6–8]等。但双体船水下噪声相关研究仍旧较少。就双体船水下噪声而言，两侧潜体对于水下噪声传播的影响是该问题的特殊之处和难点。声固耦合法已经被证明在船舶水下噪声研究中具有良好的适用性与准确性[9–12]，为此本文即采用该方法，对双体船水下近场噪声特性进行分析与讨论，旨在为双体船结构声学设计及低噪声使用提供参考。

1 声固耦合法

声固耦合有限元法的基本原理是：首先，将船体结构离散，对于船体结构，利用节点处的位移连续和力平衡条件建立船体结构的质量矩阵和刚度矩阵，求解节点处的结构响应，并通过预先定义的形函数求解节点间的结构响应；同时，将流场离散，根据理想流体的声波运动方程，建立流场节点之间的位移连续和力平衡关系，结合流场与船体结构间的耦合关系（质点振动速度连续和声压相等）、流场外边界的边界条件和自由面条件，求解流场域内流场节点处的声压，并通过预先定义的形函数求解节点间的声压值[9]。

1.1 无限流场的模拟

对于简谐激励作用下的结构振动，在外部流体介质中产生的辐射声压p(r)满足Helmholtz方程、流固界面条件以及Sommerfeld条件[9]

式中：k=ω/c为波数，ω为圆频率，ρ为流体介质密度，n为结构表面S的外法向单位矢量，vn为结构表面S的外法向振速，r=Q-P，Q为结构表面S上的任意点，P为空间中的任意点[9]。方程(3)的基本解为

利用格林公式和相应的外场问题声学边界条件，可得到采用声压p(P)与法向振速vn表示的外场问题的Helmholtz直接边界积分方程[9]

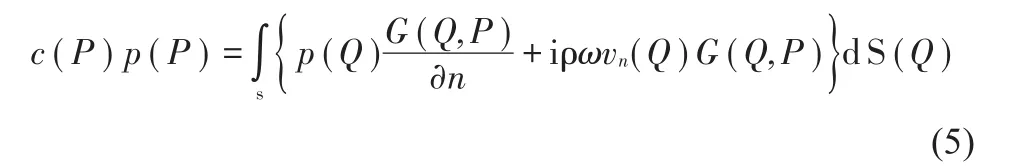
式中：c(P)为归一化位置角（位置角是指空间点P相对于结构位置点不同而形成的与水平方向的空间角度），对应不同的区域，c(P)有不同的值：当P为外部流场域的点时，c(P)=1；当P为结构表面处的点时，c(P)=0.5；当P为结构内部区域的点时，c(P)=0。

1.2 结构流体耦合振动方程

假定流体是理想的声学介质，则声波动方程为

式中：c为流体介质中的声速；p为瞬时声压。

应用Galerkin法，并乘以声压的变分δp，在流体区域内积分，经过运算得[13]

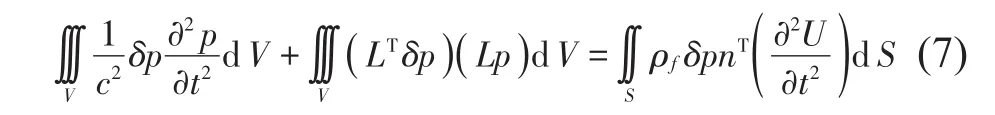
式中：U为S面上位移向量 ；。

将流体方程离散化，分成若干个有限单元，单元内任意点的声压和质点的位移及其对时间的各阶导数均可由该单元节点上相应值插值表示，并将声压变分约去，可得到完全耦合的结构流体运动方程[9]

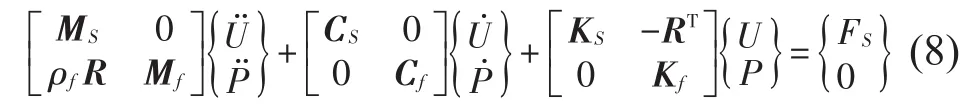
式中：MS、CS、KS分别为结构质量矩阵、结构阻尼阵和结构刚度矩阵，Mf、Cf、Kf分别为流体质量矩阵、流体声阻尼矩阵和流体刚度矩阵，R为流体和结构的耦合矩阵，U、P分别为节点位移向量和声压向量，FS为结构载荷向量[9]。

2 双球壳水下近场噪声预报模型

在直接对双体船水下近场噪声特性进行分析之前，首先将其抽象为两个完全相同的球壳，而后基于声固耦合法对该双球壳模型进行近场噪声特性研究。本文所采用的双球壳半径R为1 m，球心间距D取10 m。球壳视为耐压结构，完全浸没水中，并建立单球壳模型以作对比。流场域尺度及边界条件会对双球壳机械噪声预报结果产生影响，根据双球壳结构特点及计算精度要求，建立流场域如图1所示。

流场为半球形、半圆柱以及矩形的组合体，与球壳通过Tie耦合方式紧密连接，其水线面按自由液面处理，其他表面按照无反射边界面处理。球壳结构材料属性：弹性模量E=2.1×1011Pa，泊松比μ=0.3，密度ρ=7800 kg/m3。流体材料属性：声速c=1460 m/s，密度ρ=1000 kg/m3。其结构简图见图1。

为简化问题，本次计算暂不考虑结构损耗因子，激励载荷为作用于球壳顶部中心处的单位力，对双球壳模型和单球壳模型进行分别加载计算。考虑到双球壳辐射噪声的指向性以及球壳之间区域的声场变化，由于流场域内声压分布沿纵向分布相对较横向分布变化较小，且流场域横向尺寸大于纵向尺寸，因此，本次分析中沿纵向不再设置考核点，而在横向的X=0 m处球心截面处取3组考核点。分别为Z=1.5 m处每隔0.5 m等间距取37个考核点；Z=-2.5 m处直线部分每隔0.5 m等间距取21个考核点，圆周部分等间距取16个考核点，共计37个考核点；Z=0 m处17个考核点。单球壳模型与双球壳模型的考核点布置相同。双、单球壳模型各组考核点设置见图2。

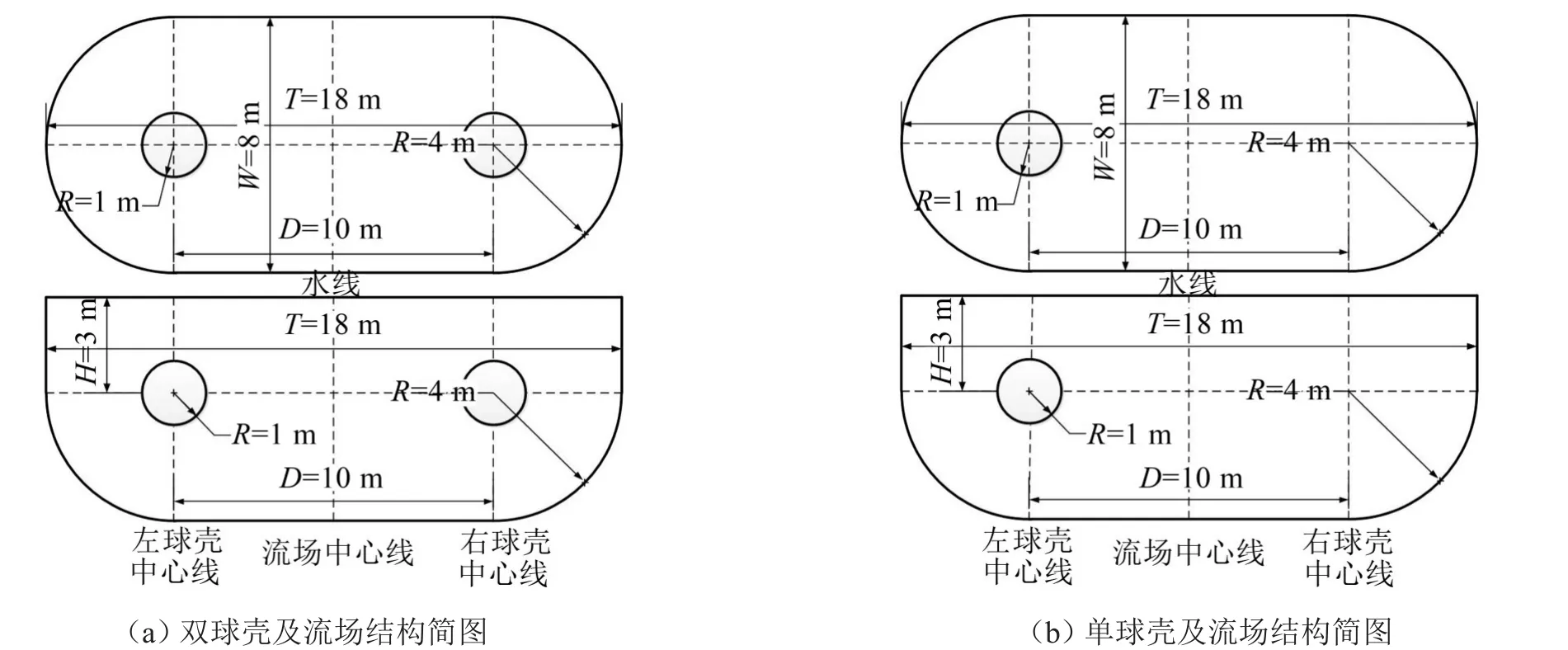
图1 双球壳及单球壳结构简图

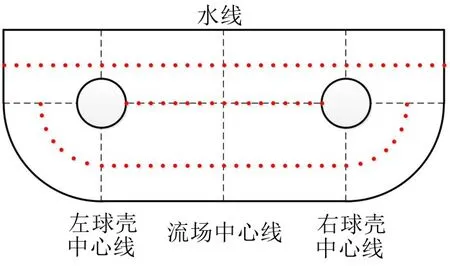
图2 双球壳模型考核点设置

3 双球壳模型水下近场噪声特性

结果显示，双球壳模型流场域在很多频点存在显著的噪声亮点。尤其在双球壳之间的近场区域，噪声亮点十分明显，在一些较高的频点出现了多个亮点。此现象并不出现于单球壳模型流场域中，可以推测这应是双球壳结构独有的声学现象。典型流场声压云图见图3。

图3 D=10 m时双球壳模型流场声压分布云图

可以看出，在双球壳水下声场的近场区域，存在着不同程度的噪声亮点，该现象的成因应是两球壳各自受激后形成各自的水下声场，两个声场相互叠加构成一个双球壳合成声场，合成声场处的声压级由两球壳受激后的辐射噪声叠加而成，当其中的波程差满足一定关系时，合成声场内部将出现驻波现象，在驻波的波峰位置即形成声压聚集区，从而形成噪声亮点。单独取出设置在流场区域内的各组声压考核点，将其双球壳模型水下机械噪声计算结果与左右单球壳水下机械噪声计算结果的叠加值做一对比，取其亮点较为明显的对比图如图4，其中LR代表左右单球壳叠加结果，L+R代表双球壳计算结果。

由图4可以看出，在双球壳水下声场的近场区域，不同位置及频点处的声压都存在大小不一的噪声亮点，在某些频率该亮点相当显著。由此可以推断，在拥有对称潜体结构以及对称激励载荷的结构物水下声场的近场区域，该现象总是存在。由此可以判断，双体船水下声场的近场区域所存在的噪声亮点现象，并不是偶然的、单一的现象，而是一种普遍存在于拥有对称潜体结构以及对称激励载荷的结构物水下声场的近场区域的现象，此种现象的显著程度与潜体间距以及声波的波长有关。

4 双体船水下近场噪声预报模型

表1 双体船模型尺寸参数

为进一步验证在双球壳模型水下近场噪声中出现的噪声亮点现象，本文开展了针对某实际双体船的水下近场噪声特性研究。该双体船为新型小水线面双体船，拥有左右潜体并没入水中，每个潜体设有一台推进电机。船体结构采用钢质建造，钢材弹性模量E=2.1×1011Pa，泊松比λ=0.3，密度ρ=7800 kg/m3。流体材料属性：声速c=1460 m/s，密度ρ=1000 kg/m3。双体船尺寸参数及结构示意图见表1及图1。

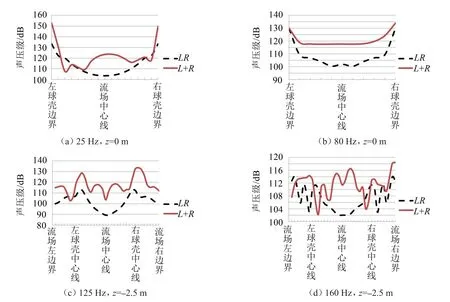
图4 典型声压对比图

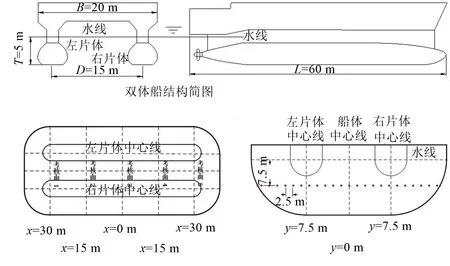
图5 考核点与考核面设置

考虑到实际双体船模型尺寸较大，其水下声场的近场区域主要是两潜体之间区域，该区域也是本次分析的重点区域，因此本次分析沿船长方向设置5个考核截面，在每个截面沿船宽方向在水线下7.5 m处等间距设置25个考核点。考核点设置如图5所示。

为便于对比分析，本文主要研究以下3个工况双体船水下近场噪声特性：1.左侧潜体受激；2.右侧潜体受激；3.双侧潜体受激。本文的主要目的，在于探索双体船水下近场噪声特性与单体船舶的差异，并不在于针对该船作精确的水下噪声预报，因此本文假设两侧潜体的推进电机载荷相同，为某船实际推进电机激励载荷经折算而来。本文的计算频率范围为20 Hz～200 Hz，载荷曲线见图6。

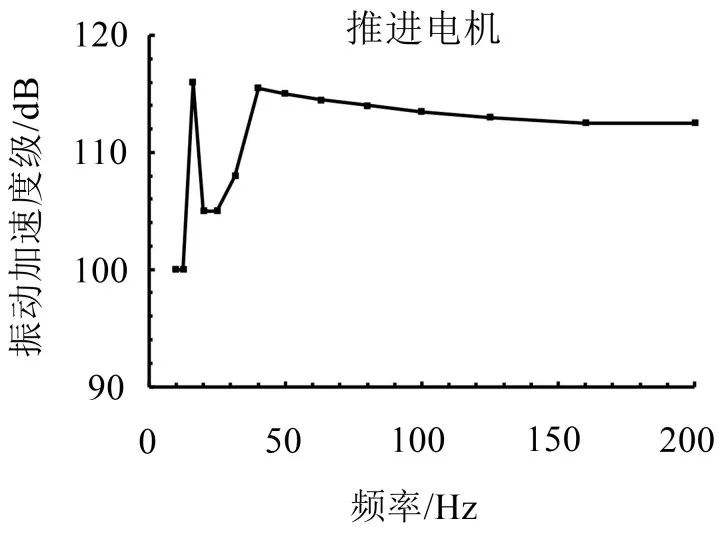
图6 推进电机激励载荷曲线

5 双体船水下近场噪声特性分析

5.1 单侧潜体激励下近场噪声特性

在单侧潜体施加激励载荷时，由于双体船对称的潜体结构形式，受激潜体一方面直接产生结构辐射噪声，形成单侧潜体声场；另一方面该辐射噪声在另一潜体产生反射，叠加于受激潜体产生的单侧潜体声场，在特定频率下将出现驻波现象，形成周期性的峰谷。在波峰处即形成噪声亮点。

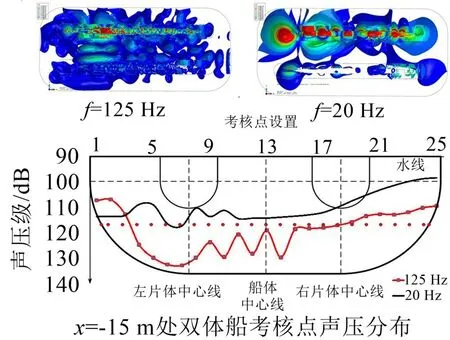
图7 单侧潜体激励下近场噪声特性

由图7可知，f=20 Hz时，双体船水下近场噪声分布特性与单体船基本相同，水下噪声声压级随距受激潜体距离增大而急速下降：f=125 Hz时，双体船两侧潜体之间近场区域出现显著的噪声亮点，该现象与单体船舶有明显不同。其原因可能是受激潜体一方面直接形成单侧潜体声场；另一方面该辐射噪声传播至另一潜体后形成反射声波，叠加于受激潜体产生的单侧潜体声场，入射、反射声波相互叠加形成驻波现象，从而形成噪声亮点。单侧潜体受到激励时的噪声亮点与激励频率、潜体中心线间距等有关。

5.2 双侧潜体激励下近场噪声特性

由5.1节已知，在单侧潜体受激时双体船在两侧潜体之间的近场区域将出现噪声亮点。由此推测，当双体船两侧潜体均施加激励载荷时，两侧潜体各自形成水下声场，其各自声场又将出现两种作用：

(1)两侧声场的直接叠加；

(2)两侧声场在经另一潜体反射后与原声场叠加。这样，将在近场形成更为显著的噪声亮点。

由图8可见，在特定频点下，双体船两侧潜体施加激励时将在水下近场产生十分显著的噪声亮点，亮点个数及位置与两侧潜体间距及声波频率密切相关。这基本上验证了本文的猜想：双体船两侧潜体均施加激励载荷时，两侧潜体各自形成自己的水下声场，该声场将在近场区域产生叠加，使得双体船水下近场噪声区域直接形成驻波现象从而形成噪声亮点；同时两侧声场又将在另一潜体处产生反射，进一步叠加于水下近场噪声，原本的亮点更为显著，从而使得双体船水下近场噪声特性迥异于常规单体船舶。

从上述结果可见，双体船由于其独特的两侧潜体结构，与连接两侧潜体的甲板一起构成了水下近场噪声的“半封闭区”。一方面，两侧潜体各自形成的水下声场由于位置对称而形成驻波现象，进而形成噪声亮点；另一方面，“半封闭区”内的声波往往在两侧潜体、甲板之间多次反射，使得声能在该区域大量聚集，进一步加强了亮点处的声能，这是双体船水下近场噪声的独特之处。

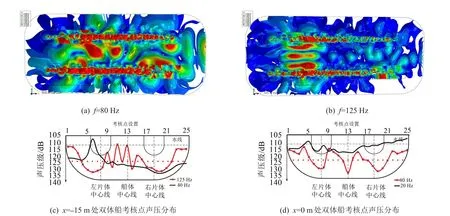
图8 双侧潜体激励下近场噪声特性

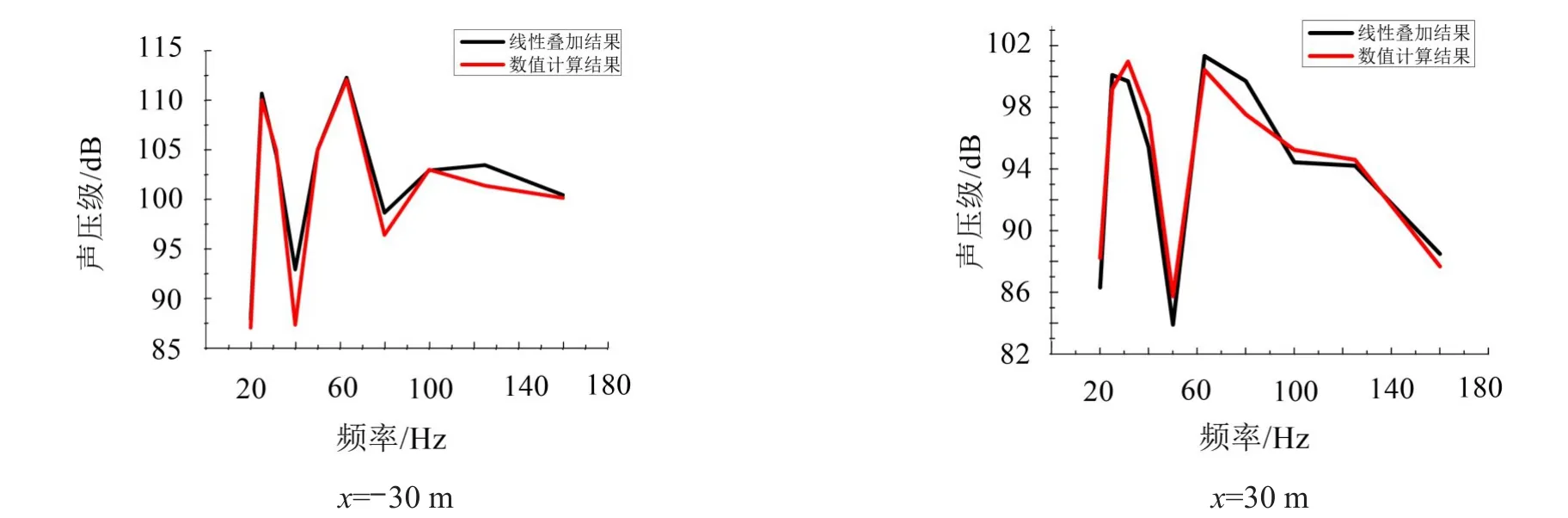
图9 双体船远场水下噪声特性

6 双体船水下辐射噪声的远场特性

一般而言，多个声源在其合成声场的远场区域，其声压级分布大致满足线性叠加原理，双体船水下远场声辐射是否满足线性叠加原理仍有待于进一步研究。为考察双体船水下远场噪声情况，本文根据能量叠加原理，将中低频不同考核面的左右潜体单侧激励计算结果叠加，并与双侧激励的计算结果进行了对比分析。图9为x=-30 m和x=30 m考核面处左右潜体单侧激励计算结果的声压线性叠加与双侧潜体同时激励的数值计算结果的对比。

由图9对比曲线可知，双体船水下辐射噪声虽然在不同频点以及考核点处的左右潜体单侧激励的叠加结果与双侧激励计算结果的吻合程度不尽相同；但总体而言，各考核点声压基本满足线性叠加原理计算结构。由此可见，双体船水下远场辐射噪声大致满足线性叠加原理，即双体船水下机械噪声总声级可通过单机辐射噪声线性叠加得到

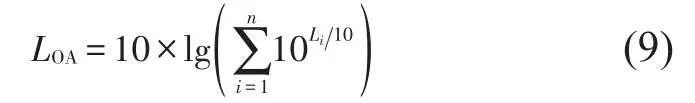
式中：LOA为双体船水下机械噪声总声级，Li为双体船单机设备辐射噪声声源级。

7 结语

（1）双球壳模型水下声场近场区域存在噪声亮点，且该现象并不是偶然的、单一的现象，而是一种普遍存在于拥有对称潜体结构以及对称激励载荷的结构物水下声场近场区域的普遍现象，此种现象的显著程度与潜体间距以及声波的波长有关。

（2）双体船在单、双侧潜体施加激励载荷时，受激潜体一方面直接产生结构辐射噪声，形成单侧潜体声场，另一潜体作为弹性边界产生相应的散射及收到声激励后产生二次辐射，从而形成近场噪声亮点。双侧潜体受激时该现象更为显著。

（3）双体船在双侧激励作用时，其远场辐射噪声大致满足线性叠加原理，并可由式（9）得到，即双体船结构远场辐射噪声可依据线性叠加原理由单机辐射噪声线性叠加获得。

（4）由上可知，双体船结构在单侧潜体受激、双侧潜体受激的工况下，均会呈现水下近场噪声亮点现象。由于双体结构形式的科考船、测量船等船舶大多以左右双机并开的形式进行作业，其水下近场噪声将由此产生噪声突出问题，从而影响正常科考、测量活动，因此该类船舶应针对近场噪声问题做好防护设计并避开近场工作区域。

[1]姚熊亮，王献忠，孙龙泉，等.复杂结构中频声振问题的方法研究[J].振动工程学报，2011(4)：444-449.

[2]庞福振.船舶结构噪声截断模型数值预报方法研究[D].哈尔滨：哈尔滨工程大学，2012.

[3]邹春平，陈端石，华宏星.船舶结构振动特性研究[J].船舶力学，2003(2)：102-115.

[4]邹春平，陈端石，华宏星.船舶水下噪声特性研究[J].船舶力学，2004(1)：113-124.

[5]邹春平，陈端石，华宏星.船舶结构振动模态综合法[J].上海交通大学学报，2003(8)：1213-1218.

[6]周其斗.细长壳体水声辐射问题的有限元结合边界元解法[J].海军工程学院学报，1996(2)：35-44.

[7]王路才，周其斗，纪刚.纵桁对环肋圆柱壳体水下振动与声辐射的影响[J].海军工程大学学报，2012(2)：87-92.

[8]王路才，周其斗，纪刚，等.以舱段模型代替整艇模型进行噪声估算的可行性探讨[J].中国舰船研究，2010(6)：26-32.

[9]缪旭弘，钱德进，姚熊亮，等.基于ABAQUS声固耦合法的水下结构声辐射研究[J].船舶力学，2009(2)：319-324.

[10]缪旭弘，王雪仁，贾地，等.大型复杂圆柱壳中高频振动噪声仿真计算方法研究[J].计算力学学报，2012(1)：124-128+134.

[11]金广文，章林柯，缪旭弘，等.水下加肋双层圆柱壳体振动传递特性分析[J].振动与冲击，2011(5)：218-221.

[12]庞福振，姚熊亮，缪旭弘，等.设备对船体结构的激励力及其应用研究[J].工程力学，2012(7)：283-290.

[13]GROTE M,J KELLER.On nonreflecting boundary conditions[J].Journal of Computational Physics,1995,122:231-243.