四轮独立驱动轮毂电机电动汽车主动避撞模糊控制

郝克宇， 廉宇峰*， 陈 刚， 陈 亮，金 晶， 唐重和

(1.长春工业大学 电气与电子工程学院， 吉林 长春 130012;2.中油管道长春输油气分公司， 吉林 长春 130022;3.大陆汽车电子(长春)有限公司， 吉林 长春 130032;4.大陆汽车电子(长春)有限公司净月分公司， 吉林 长春 130022;5.西门子工厂自动化工程有限公司， 吉林 长春 130012)

0 引 言

随着车辆持有量的大幅增长，能源危机和交通安全问题日益突出，电动汽车的发展和先进的汽车安全技术引起了各界的广泛关注。由于电动汽车采用四轮轮毂电机驱动(four-in-wheel-motor-driven, FIWMD)系统，具有较高的能源利用效率和环保优势。除此之外，电动汽车的转矩容易测量且精确，响应速度也较快。主动避撞 (Active Collision Avoidance, ACA) 控制系统可以从节能性和安全控制方面显著提高车辆的性能[1]。

在ACA控制系统中，纵向安全距离模型和模糊逻辑控制器作为两个关键技术，逐渐成为研究的重点。近年来，已有不少研究人员将他们的研究重点放在自车与前车之间的安全距离模型及其在ACA系统中的应用。提出了一些典型的安全距离模型，如MAZDA，HONDA模型等[2]。为了进一步了解电动汽车的ACA系统，文中提出了一种新的安全距离模型来提高电动汽车的安全性。模糊逻辑控制作为一种前沿的现代控制方法，越来越多的被研究人员用来实现ACA控制系统。一种基于简化永磁同步电机模型(Permanent Magnet Synchronous Motor, PMSM)的模糊逻辑控制器在文中被提及，用来实现FIWMD电动汽车系统的设计。提出了简化的PMSM模型来估计电机的实际力矩和期望力矩。ACA控制系统中，模糊逻辑控制器输出系统所需期望加速度，安全距离模型中提供了模糊逻辑控制器所需的约束条件。实际加速度可以在CarSim的车辆动态模型中获得，期望加速度和实际加速度组成一个反馈系统。

文中针对四轮轮毂驱动电动汽车的ACA系统，采用分层式四轮轮毂驱动电动汽车主动避撞控制器的设计，可以根据不同用途进行任意搭配。因此，文中采用分层式控制结构。上层控制器根据行车感知系统获取本车信息、两车间距信息及驾驶员相关信息等，确定当前情况下自车所需要的期望加速度；期望加速度既作为上层控制器的输出,同时作为下层控制器的输入，进一步控制车辆动力学系统，输出系统所需要的期望加速度。由于单一线性建模方法的不足，文中运用CarSim2016和Matlab/Simulink联合仿真，建立能够模拟四轮轮毂驱动电动汽车实时工况，同时反映主动避撞系统的动态性能，并能够兼顾模型精确性的动力学模型。文中采用模糊逻辑控制理论和PI控制理论，设计了适合ACA系统的控制器，并且对典型城市和高速工况进行仿真与验证。

1 车辆纵向动力学

四轮轮毂驱动电动汽车主动避撞系统功能的实现涉及到车辆纵向动力学模型，文中引用了一个车辆纵向动力学模型，将四轮轮毂驱动电动汽车纵向的受力情况十分明确地表示出来[3]。车辆在斜坡上运动，受车辆外部纵向力的影响，包括轮胎纵向力、轮胎滚动阻力、空气阻力和车辆自身的重力，车辆在坡路上行驶的受力分解图如图1所示。

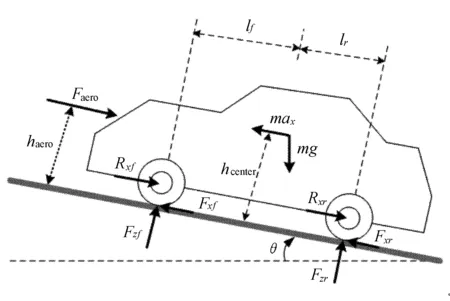
图1 车辆纵向受力图

车辆的纵向加速度根据牛顿第二定律可以被描述为：

max=Fxf+Fxr-Rxf-Rxr-Faero-mgsinθ

(1)

式中：m——整车的总质量;

ax——车辆在质心上的纵向加速度；

Fxf——前轮轮胎纵向力；

Fxr——后轮轮胎纵向力;

Rxf——前轮的滚动阻力；

Rxr——后轮的滚动阻力；

Faero——纵向的空气阻力;

g——重力加速度；

θ——电动汽车行驶路面的坡度。

如果电动汽车的行驶方向x指向左边,则定义θ的正方向为顺时针。如果电动汽车的行驶方向x指向右边,则定义θ的正方向为逆时针。lf为电动汽车质心到前轴的距离,lr为电动汽车质心到后轴的距离,并且L=lf+lr。

由转矩平衡可以获得各个轮胎的垂直载荷，即：

(2)

式中：Fzf——车辆前轮的垂直载荷；

Fzr——车辆后轮的垂直载荷；

hcenter——车辆质心距离水平面的垂直高度。

2 纵向安全距离模型

纵向安全距离模型是ACA系统的重要组成部分，电动汽车纵向的安全性和道路的利用率取决于纵向安全距离模型搭建的准确程度。对于驾驶员而言，所有必要的警报信息都与安全距离模型一起提供，并且由来自安全距离模型的信息而启动ACA系统。 如果安全距离过大，交通流量将受到影响。反之,如果安全距离太小，车辆的事故率就会大大增加。因此，安全距离模型的设计取决于是否能够适应复杂多变的交通环境，有效地平衡驾驶过程的安全性和道路利用率。

后车通过车载雷达感知前车的速度变化和加速度变化，并在领先车辆状态发生变化时，ACA系统迅速地对自车进行牵引或者制动，使两车实际的相对距离始终保持在安全范围，保证驾驶员及乘客的安全。在制动或牵引过程中，两车实际相对距离变化趋势如图2所示。

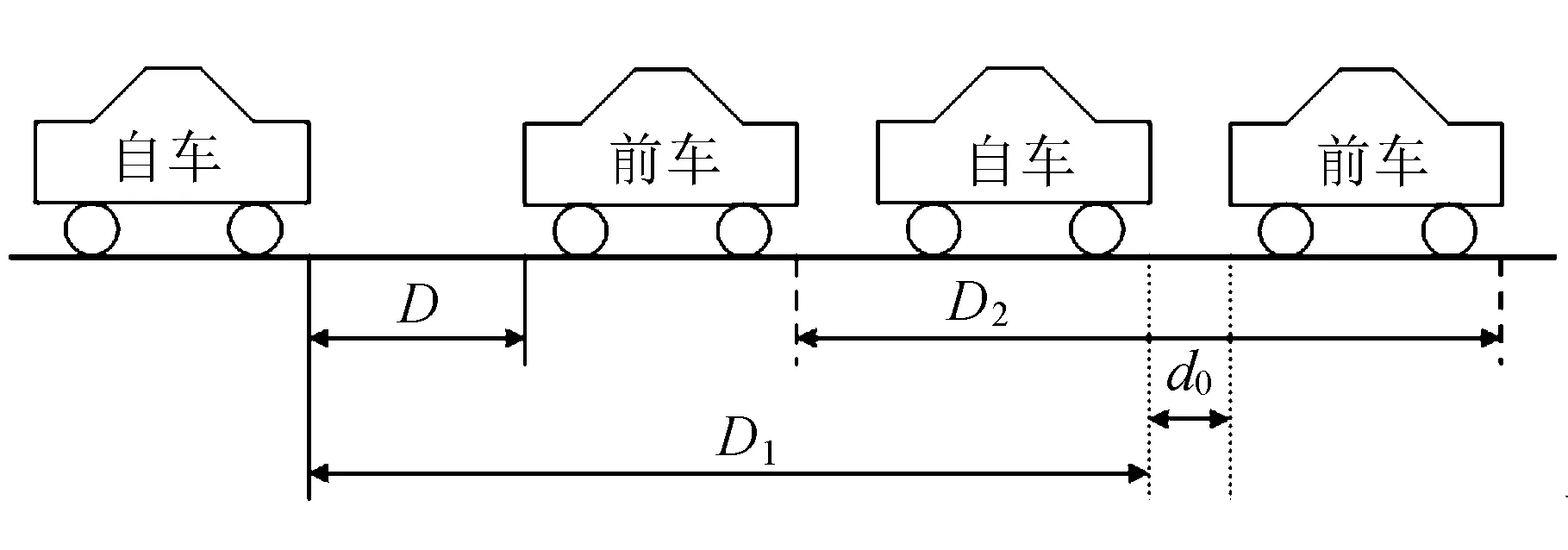
图2 车间距变化趋势图

图中，D为两车之间的距离；D1为自车行驶的距离;D2为前车行驶的距离;d0为两车最小保持距离，一般值为2～5 m[4]。Dbr为后车的制动距离。 当两车之间的距离小于或等于自车减速制动的距离时，自车的减速制动距离可以被描述为：

Dbr=D1-D2+d0

(3)

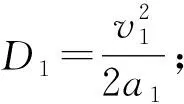
(4)

式中：a1——自车的加速度；

a2——前车的加速度；

v1——自车的速度；

v2——前车的速度。

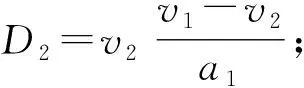
3 主动避撞控制系统设计

四轮轮毂驱动电动汽车ACA系统采用了分层式控制结构设计，由上层和下层控制器组成。上层控制器和下层控制器可以根据不同的目的进行组合，对深入研究ACA系统十分有利。上层控制器根据行车信息感知系统获取的自车速度的变化和车载雷达系统感知的车间距离，将以上信息作为模糊逻辑控制器的输入，从而得到自车在当前情况下所需要的期望加速度；所得的期望加速度既是上层控制器的输出，同时也是下层控制器的输入，从而实现对车辆动力学系统的控制，使自车加速度的值尽可能地靠近期望加速度的值。ACA系统的仿真模型如图3所示。

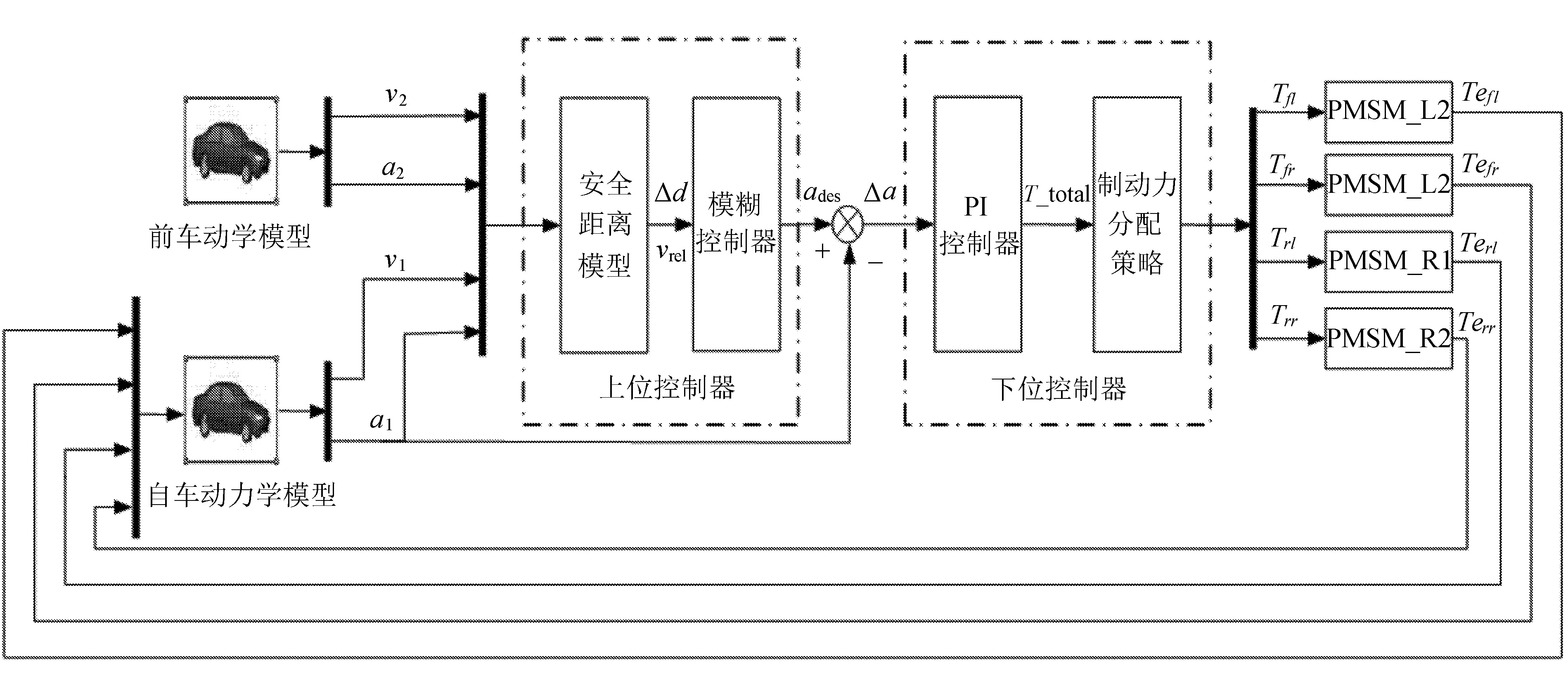
图3 ACA系统仿真模型

3.1 基于模糊控制上层控制器设计

为适应各种交通工况并满足驾驶员实际驾驶的各种要求，文中设计基于模糊逻辑控制的上位控制器，其结构如图4所示。

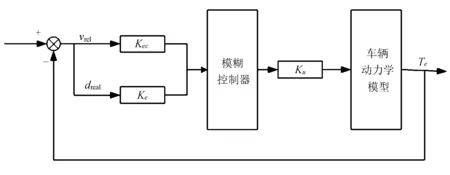
图4 模糊上位控制器模型

将驾驶员实际的驾驶特性作为考虑因素，为了更好地控制车辆，驾驶员必须了解车辆的性能，并估计自车与前车之间实际的相对距离，同时也需要估计自车与前车相对速度的差值，即：

(5)

式中：dreal——当前时刻两车实际的车间相对距离；

d1——当前时刻自车所走的距离；

d2——当前时刻前车所走的距离；

d3——初始时刻自车和前车的初始距离；

vrel——当前时刻自车与前车的相对速度。

如果相对距离dreal很大，而相对速度vrel较小，则驾驶者会以适合的加速度加速行驶，缩短车间距离，从而道路的交通效率会得到提高；如果相对距离dreal较小，而相对速度vrel较大，则驾驶者会以适当的减速度减速行驶，从而最大限度地降低车辆发生追尾事故的几率。在实际中，驾驶员是通过踩刹车或油门来使车辆减速或加速，改变车辆的行驶状态，模糊逻辑理论可以被用来描述这几种驾驶行为。

根据以上条件，一个双输入、单输出的模糊逻辑控制器在文中被采用，以跟随车和目标车之间实际的相对距离dreal和跟随车和目标车的相对速度vrel作为模糊逻辑控制器的输入信号，以跟随车期望加速度ades作为模糊逻辑控制器的输出信号，为了使ACA系统所获得的期望加速度ades更加精确，基于以上条件有必要将输入信号和输出信号进行模糊化处理[6]。

将输入转化为11个模糊集合：正正小(PPS)、正大(PB)、正中(PM)、正小(PS)、正零(PZ)、零(ZO)、负零(NZ)、负小(NS)、负中(NM)、负大(NB)、负负小(NNS)。

输出信号转化为9个模糊集合：正大(PB)、正中(PM)、正小(PS)、正零(PZ)、零(ZO)、负零(NZ)、负小(NS)、负中(NM)、负大(NB)。

3.1.1 输入、输出模糊化

电动汽车ACA系统通常的工作环境为中速、低速碰撞，所以根据实际数据设定自车和前车相对车速的变化范围为[-10,10] m/s，比例因子Kec=1，则ACA系统相对车速的模糊论域取[-10,10]。

根据现有传感器测距距离和实际数据，设定自车和前车期望车距与实际车距的差值的变化范围为[0,200] m, 比例因子Ke=0.1，则ACA系统相对车距的模糊论域取[0,20]。

将驾驶员能接受的冲击度范围和ACA系统的实际操作性作为考虑因素，将自车加速度的变化范围定义为[-4,4] m/s2,比例因子Ku=1，则ACA系统所需的期望加速度的模糊论域取[-4,4]。

3.1.2 隶属度函数的确定

作为输入信号，两车的实际相对车距和两车实际相对速度的隶属度函数采用三角波函数(trimf)。

两车实际相对车距模糊论域被分成11个部分，具体分布如图5所示。

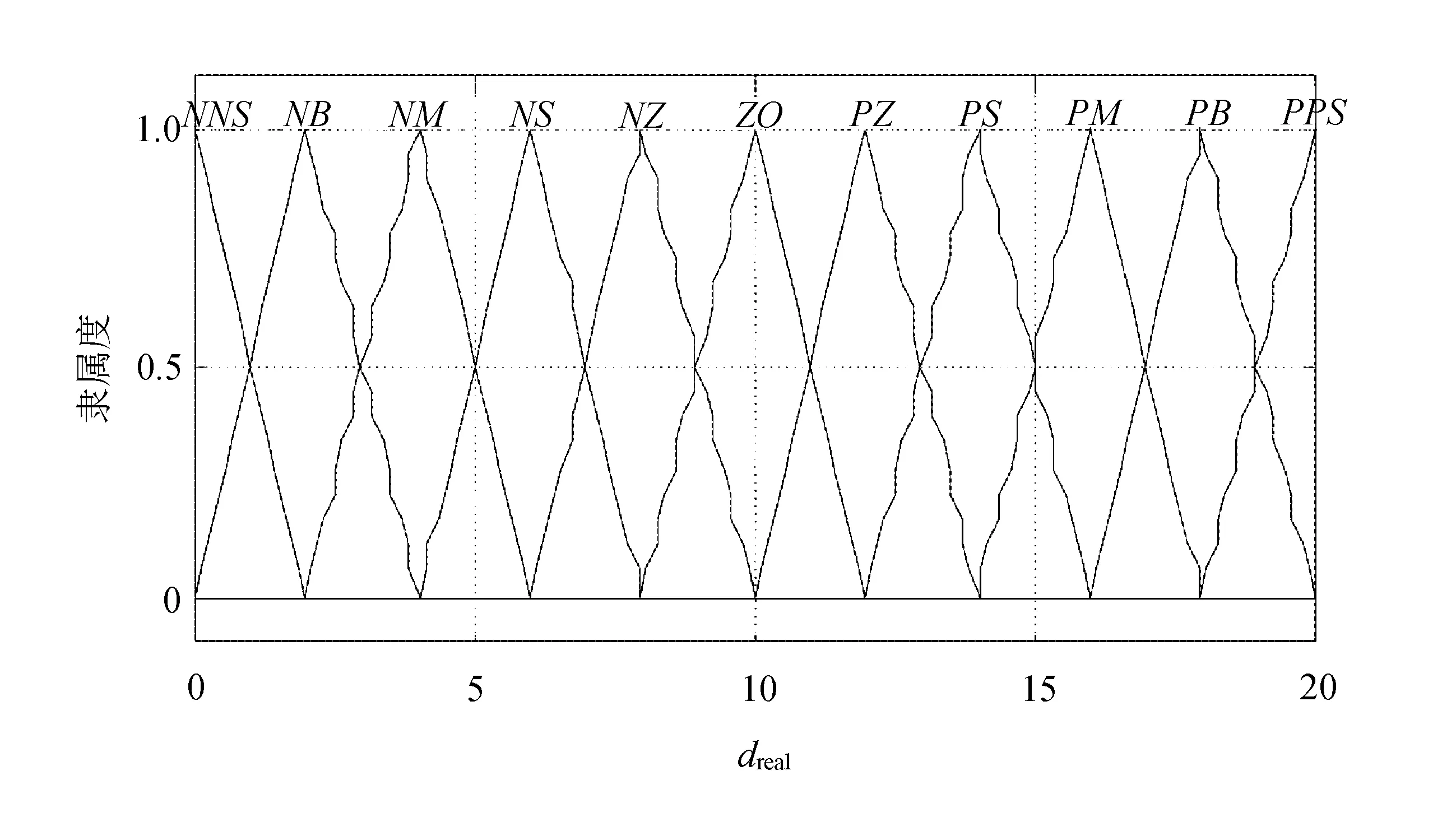
图5 相对距离的隶属度函数

两车实际相对速度模糊论域被分成11个部分，具体分布如图6所示。

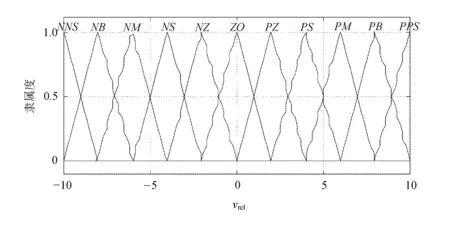
图6 相对速度的隶属度函数

作为输出信号，期望加速度的隶属度函数同样采用三角波函数，模糊论域被分成9个部分，具体分布如图7所示。

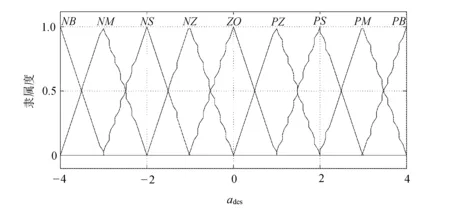
图7 期望加速度的隶属度函数

3.1.3 模糊控制规则库的建立

根据驾驶员的驾驶经验和实际的实验数据，文中将ACA系统的以下几种情况考虑在内：

1)vrel非常小、dreal非常大时，前车速度与自车速度之间的差距非常小，并且前车和自车的车间距离差距非常大，相对来说，此时自车的危险程度较小，可以适当加速行驶或保持当前车速行驶。

2)vrel非常大、dreal非常小时，前车速度与自车速度之间的差距非常大，同时自车和前车的车间距离差值非常小，此时自车的危险程度很大，应该立即进行制动，从而将自车的速度降低到安全范围之内，避免自车与前车发生追尾事故。

3)vrel和dreal都非常小或都非常大时，此时应该对自车进行小强度的制动，从而使自车保持在安全的状态，而且小强度的制动不但保证驾驶员和乘坐人员的舒适度在合理的范围内，还确保了车辆行驶的平稳性。

文中针对以上3种情况的交通状况，综合考虑行车安全性与驾驶员和乘坐人员舒适性的关系，总的原则是将自车的安全作为第一目标，与此同时，可以适当地牺牲驾驶员和乘坐人员的舒适性，当电动汽车所需制动减速度可大可小时，应当选择较大的减速度进行制动，也就是说将自车的安全性放在第一位。根据上述驾驶经验，经过反复调试与验证，文中建立四轮轮毂驱动电动汽车ACA系统的模糊控制规则，共有121条规则，见表1。

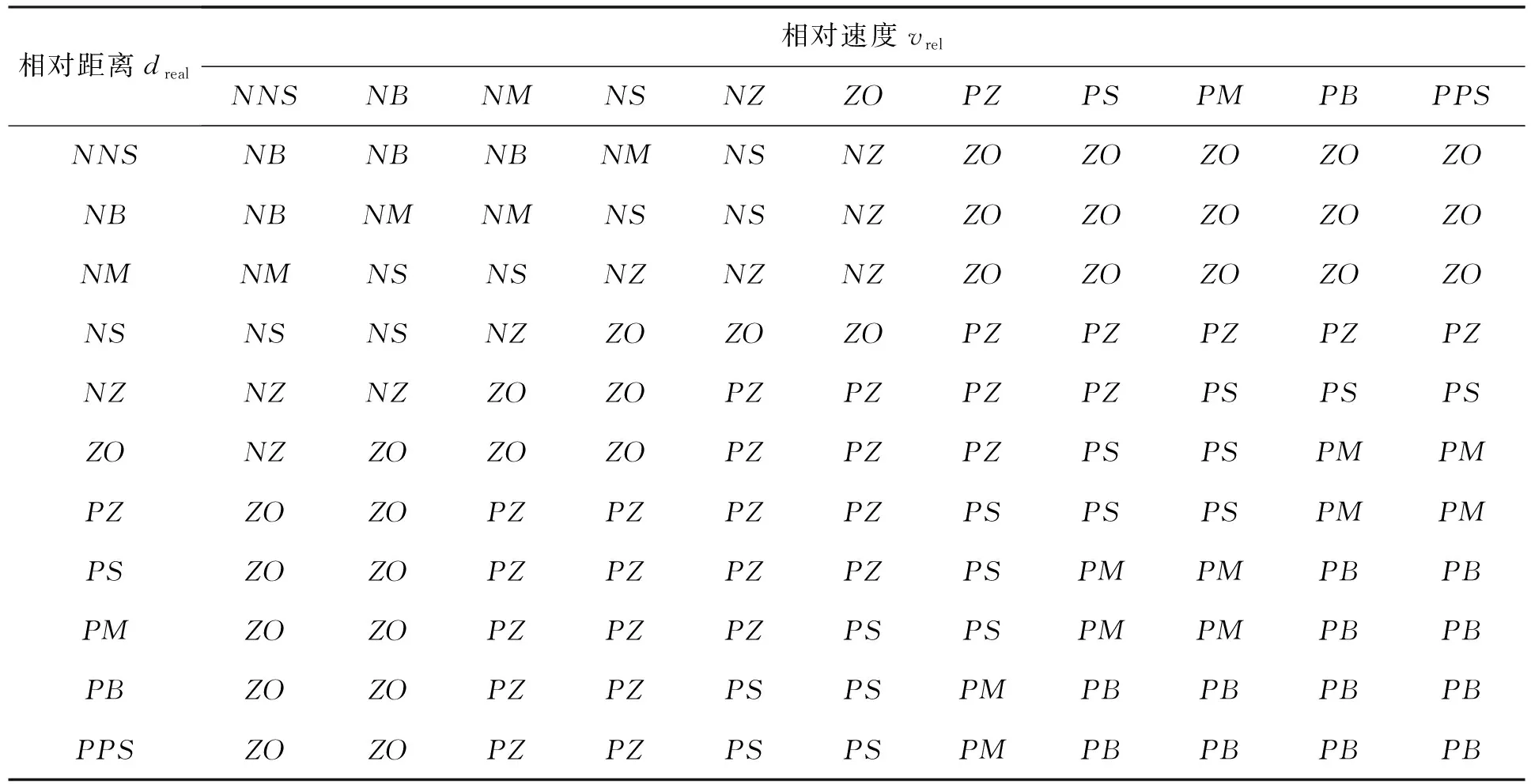
表1 ACA系统的模糊控制规则表

模糊控制系统实际上体现了输入和输出之间复杂的非线性关系，且这种关系是通过模拟人类的语言逻辑描述的，符合人类的推算过程，从而更容易被驾驶员所接受。

3.2 下层控制器设计

下层控制器由PI控制器和纵向制动力分配策略两部分组成。期望加速度不仅是上位控制器的输出，同时也是下位控制器的输入，下位控制器的输出为车辆所需要的总期望制动力，从而实现车辆的制动。下位控制器由两个计算器组成：一个是总制动力计算器，用来计算车辆制动过程中所需要的总制动力；另一个为总制动力分配器，即将计算得到的总制动力合理地进行分配，使车辆能够很好的制动，从而更好地保证车辆的安全性。下位控制器的结构见图3。

3.2.1 PI控制器设计

下位控制器中，总制动力计算器采用普遍的PI控制，该算法简单、稳定性高，同时有很好的鲁棒性，是一种普遍的研究方法，被很多研究人员所采用。PI控制算法中KP和KI值的选定是十分重要的，如果这2个值选择不合适，会给ACA系统带来很多不稳定的问题，两值确定一般常用的方法是试凑法。制动力计算器通过车辆的实际加速度和期望加速度的差值来计算出电动汽车所需要的总制动力，该调节环节中不存在任何的静差与滞后，经过反复地整定与试凑，从而比例和积分值分别为：KP=50，KI=5 000。

3.2.2 制动力矩分配策略

文中以前轮和后轮的垂直载荷为比例来分配给每个轮胎的驱动力。 结合式(1)，前后轮、左右轮纵向力可以按轮胎垂直载荷比例进行分配，得到如下方程组：

(6)

式中：ax——自车纵向实际加速度；

Tfl——自车左前轮纵向制动或牵引力矩；

Tfr——自车右前轮纵向制动或牵引力矩；

Trl——自车左后轮纵向制动或牵引力矩；

Trr——自车右后轮制动或牵引力矩；

r——电动汽车轮胎半径。

求解上述方程组，即可得到四个轮胎的制动或牵引力矩：

(7)

4 轮毂电机系统简化模型

对于FIWMD电动汽车，轮毂电机采用PMSM控制系统。PMSM控制系统具有功率密度高、功率大、体积小、控制操作性好等诸多优点。但是，PMSM控制系统也存在诸多不足，例如，系统的计算量大，且实时性较差。因此，有必要在不影响永磁同步电机性能的情况下，适当简化PMSM控制系统，从而进一步提高永磁同步电机的实时性。在寄生磁阻转矩影响排除在外的前提下，PMSM的数学模型在dq同步旋转坐标系上可以被表示如下：

(8)

式中：id——d轴上的定子电流；

iq——q轴上的定子电流；

ud——d轴上的定子电压；

uq——q轴上的定子电压；

ρ——轮毂电机的极对数；

Ls——定子电感；

Ψr——永磁磁通；

Rs——定子电阻；

B——粘滞摩擦系数；

Iω——轮胎的转动惯量；

ωr——轮毂电机角速度；

Tb——摩擦制动力矩。

简化PMSM矢量控制系统，是将转矩作为外环和电流作为内环的双闭环结构设计而成。为了简化PMSM矢量控制系统，提高ACA系统的运算速度，文中将粘滞摩擦系数B因素排除在外，采用基于空间矢量控制技术的PMSM控制系统。对电流内环来说，要求快速地跟随电流的性能，所以根据典型的I型系统来设计相应的电流内环。文中近似地将电流内环等价于一阶惯性环节，即：

式中：Ts——电流采样周期。

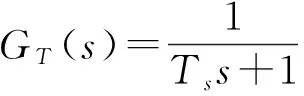
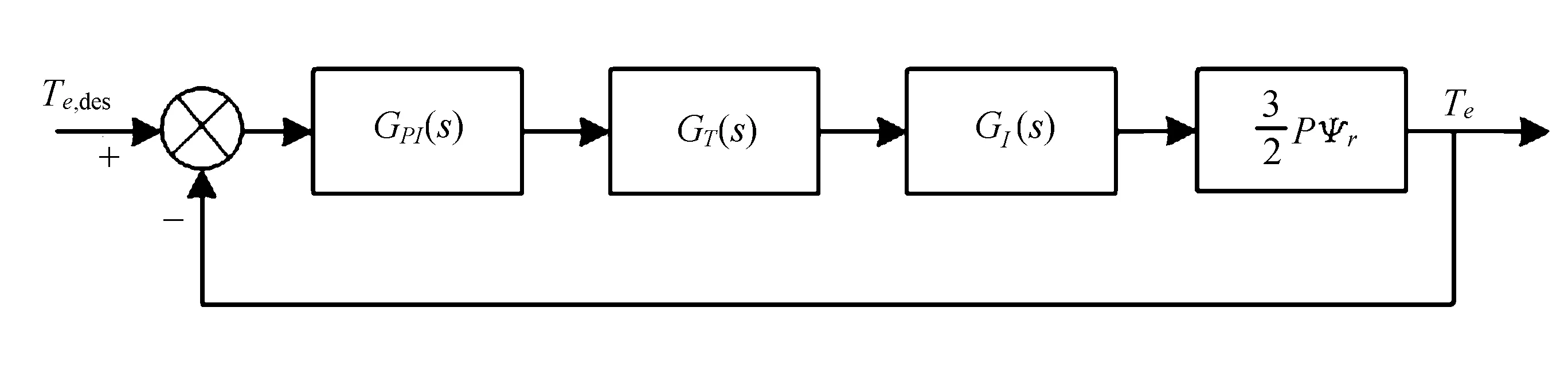
图8 PMSM矢量控制系统简化结构图

PMSM控制系统可简化为单闭环系统，以期望转矩Te,des为输入变量，以实际转矩Te为输出变量，此结构简单且易实现[7-8]。

5 仿真与实验验证

为验证电动汽车简化PMSM模型和ACA系统是否有效，文中以典型城市工况(UDDS)和高速公路工况(HWFET)作为前车的工况对ACA系统进行仿真验证。FIWMD电动汽车的整车参数和PMSM模型的参数见表2。

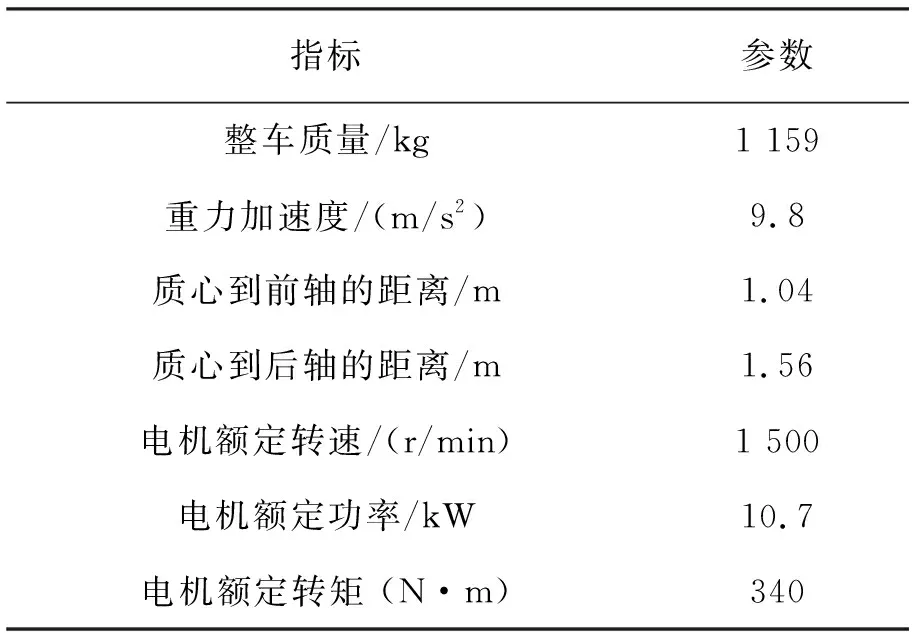
表2 FIWMD电动汽车和PMSM模型的参数

UDDS工况下，前车和自车的速度分别如图9和图10所示。

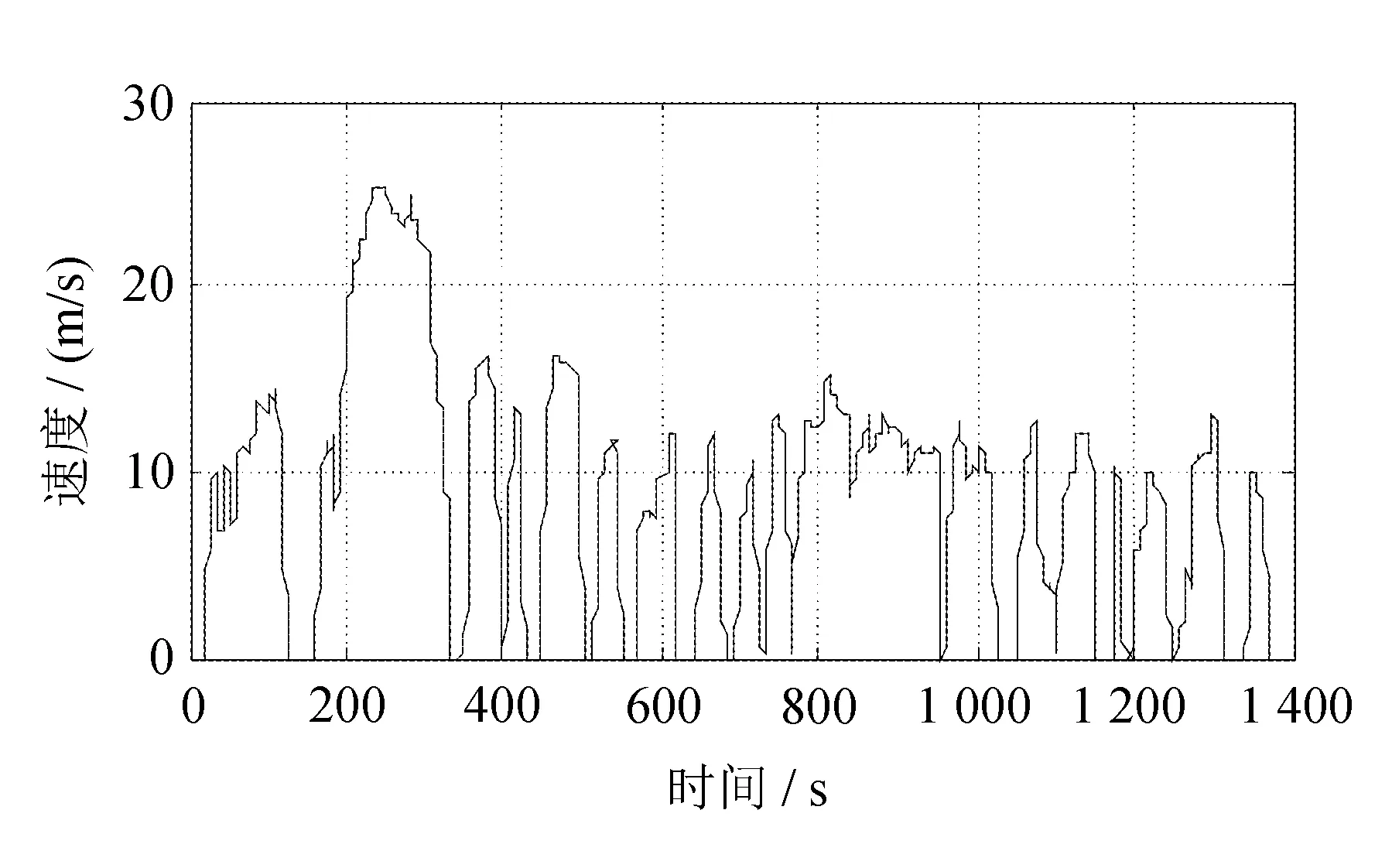
图9 UDDS前车速度

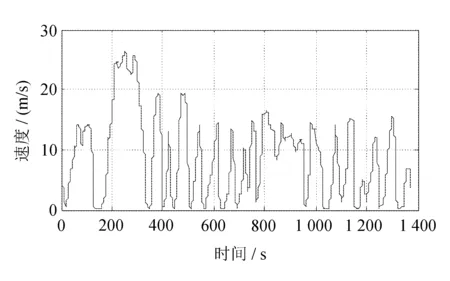
图10 UDDS自车速度

自车的实际加速度如图11所示。

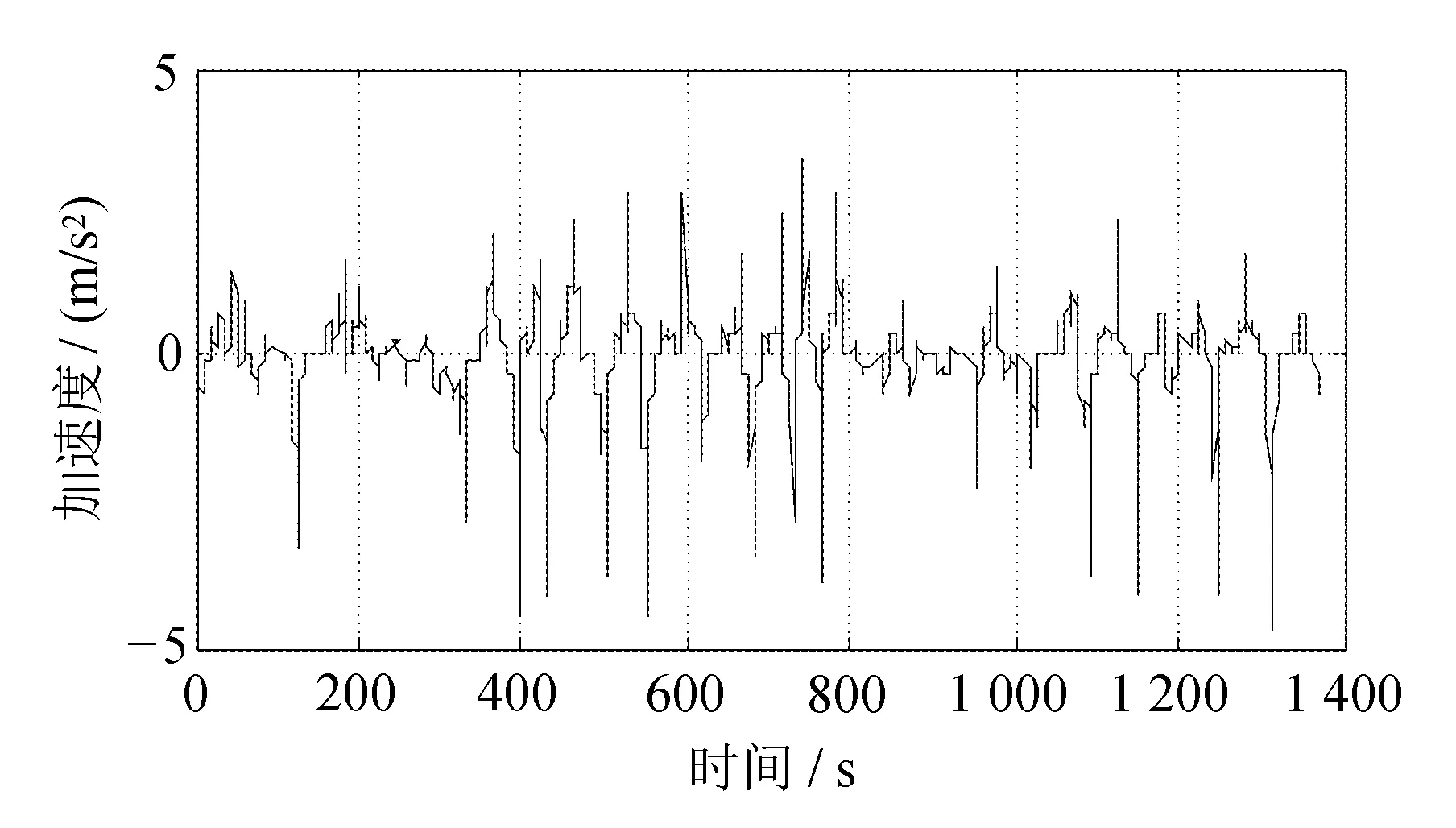
图11 UDDS自车加速度

自车左、右轮的纵向力相同。自车左前轮的纵向力与左后轮的纵向力分别如图12和图13所示。

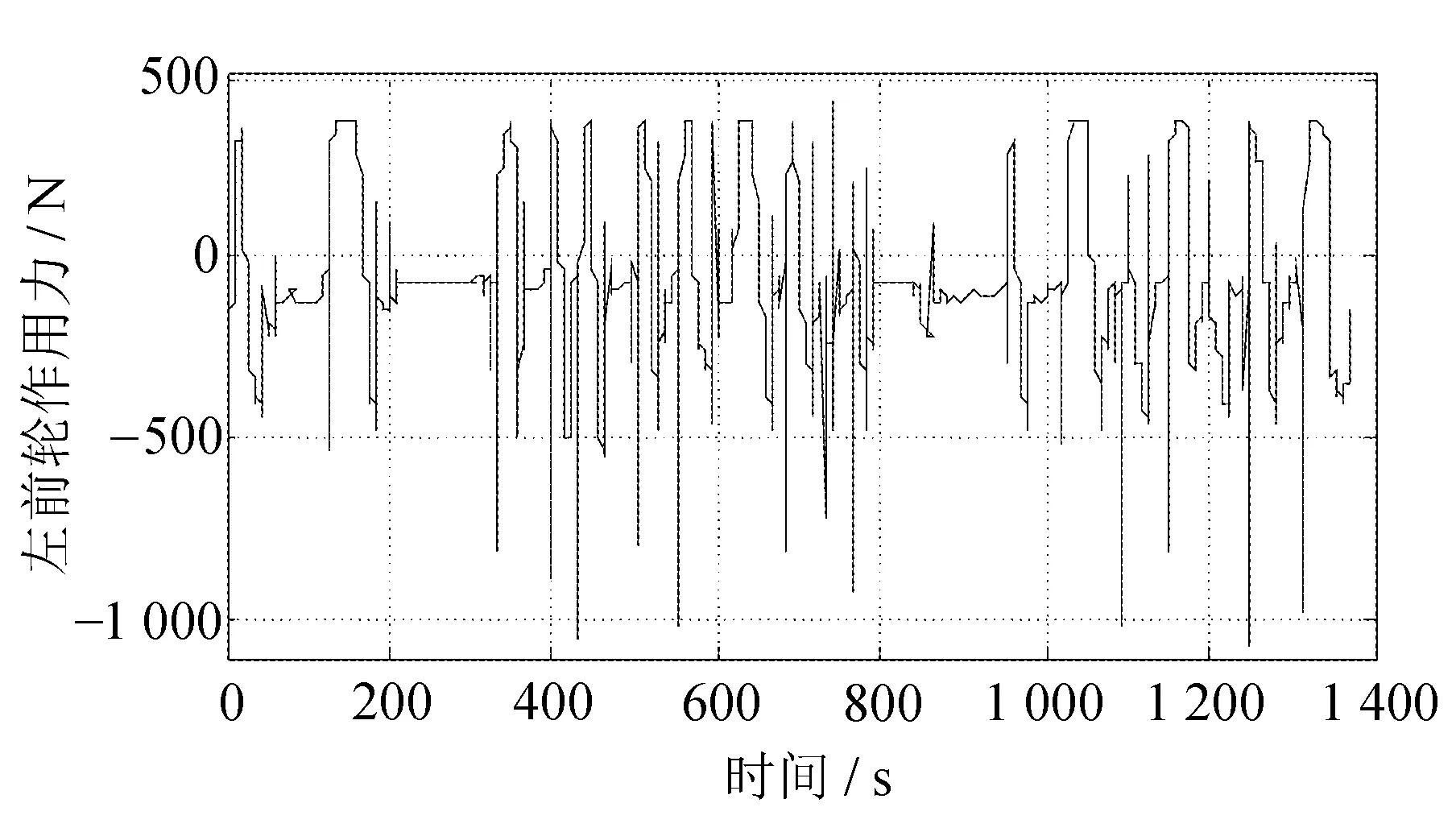
图12 UDDS自车左前轮纵向力

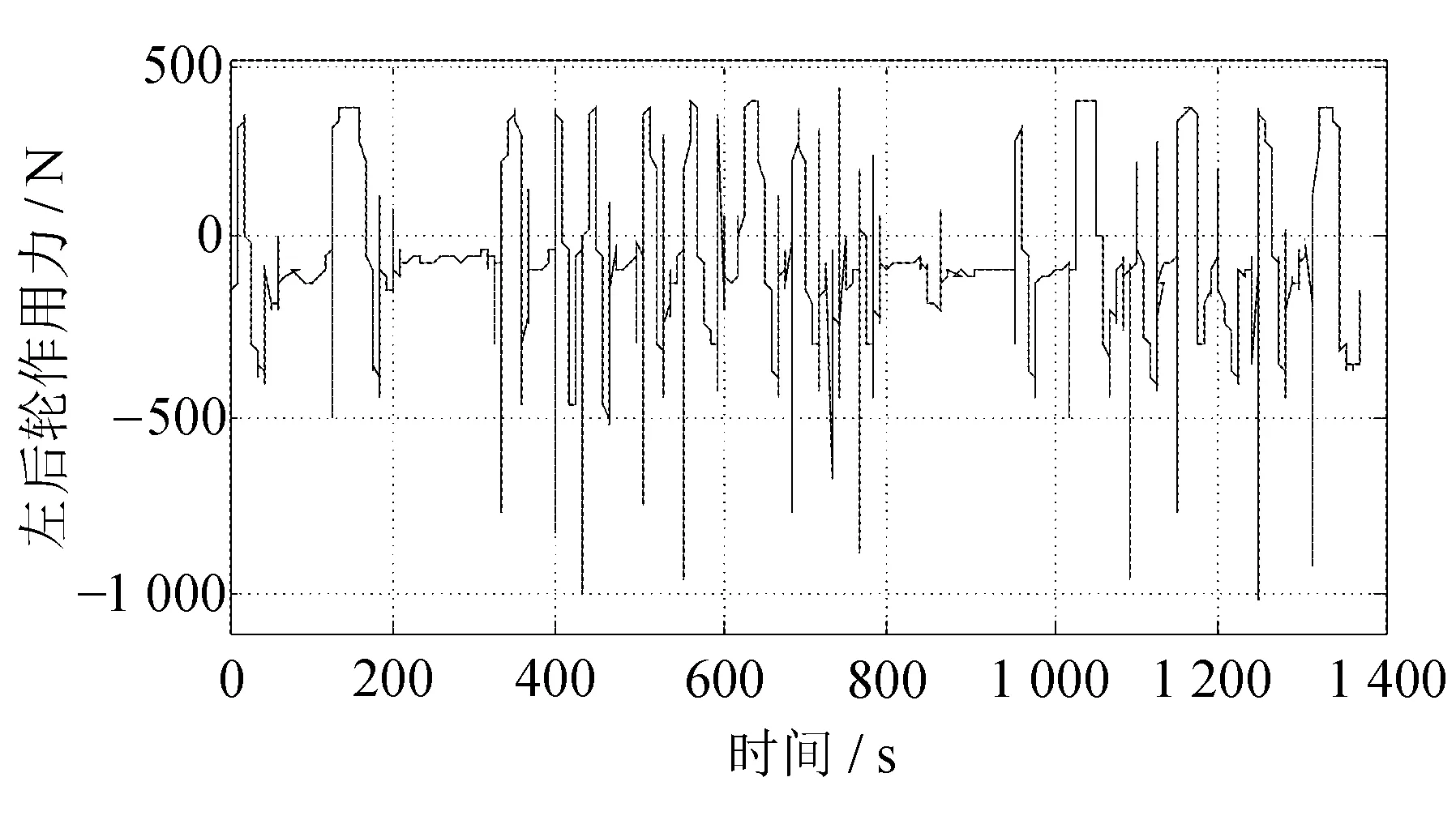
图13 UDDS自车左后轮纵向力

两车相对距离如图14所示。

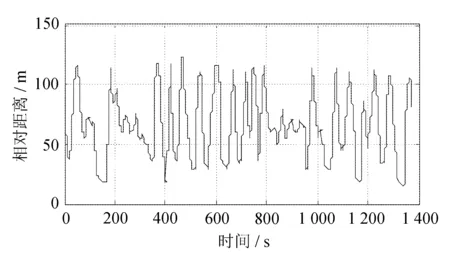
图14 UDDS两车的相对距离

HWFET工况下，前车和自车的速度分别如图15和图16所示。

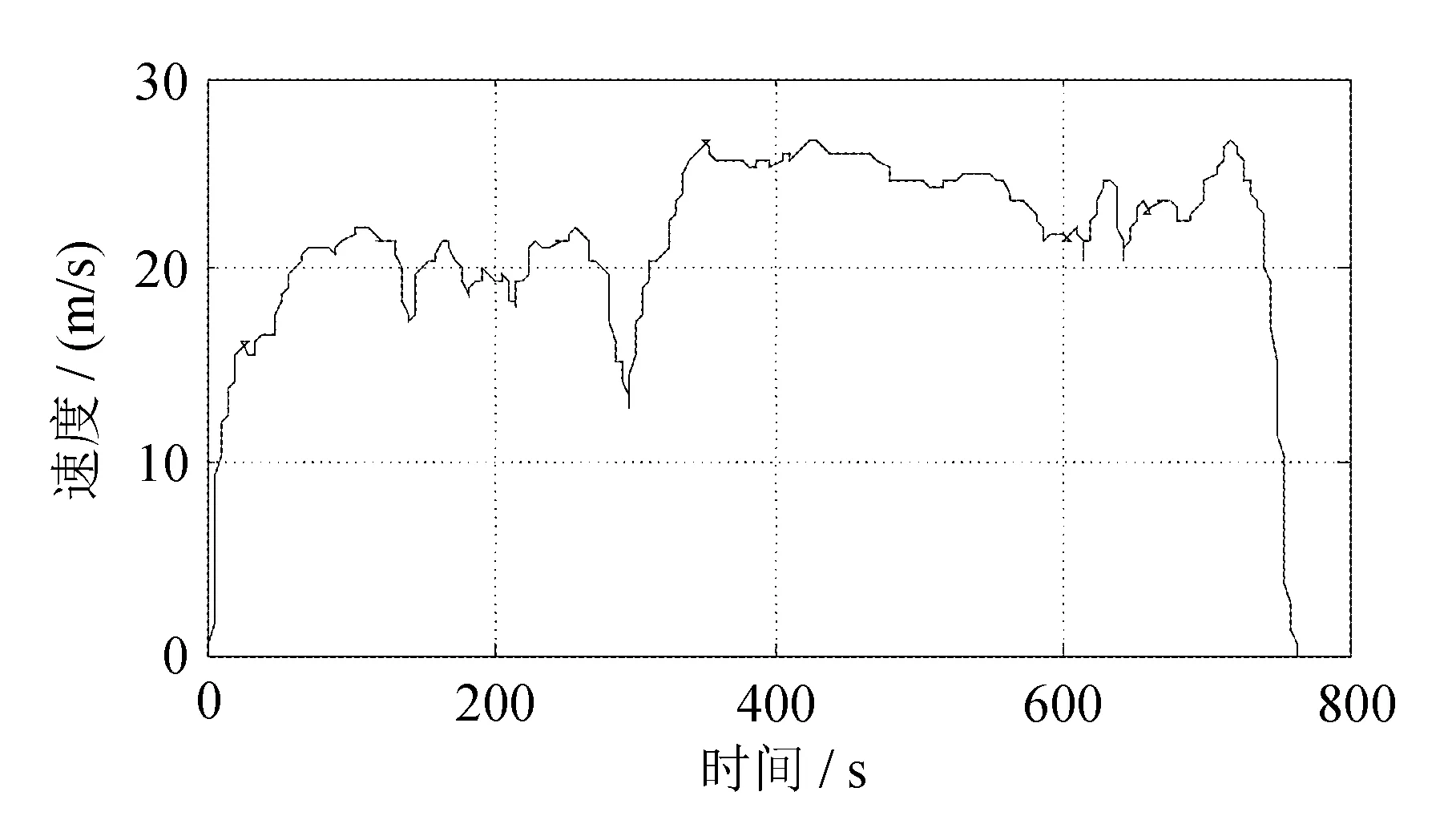
图15 HWFET前车速度

图16 HWFET自车速度

自车加速度如图17所示。

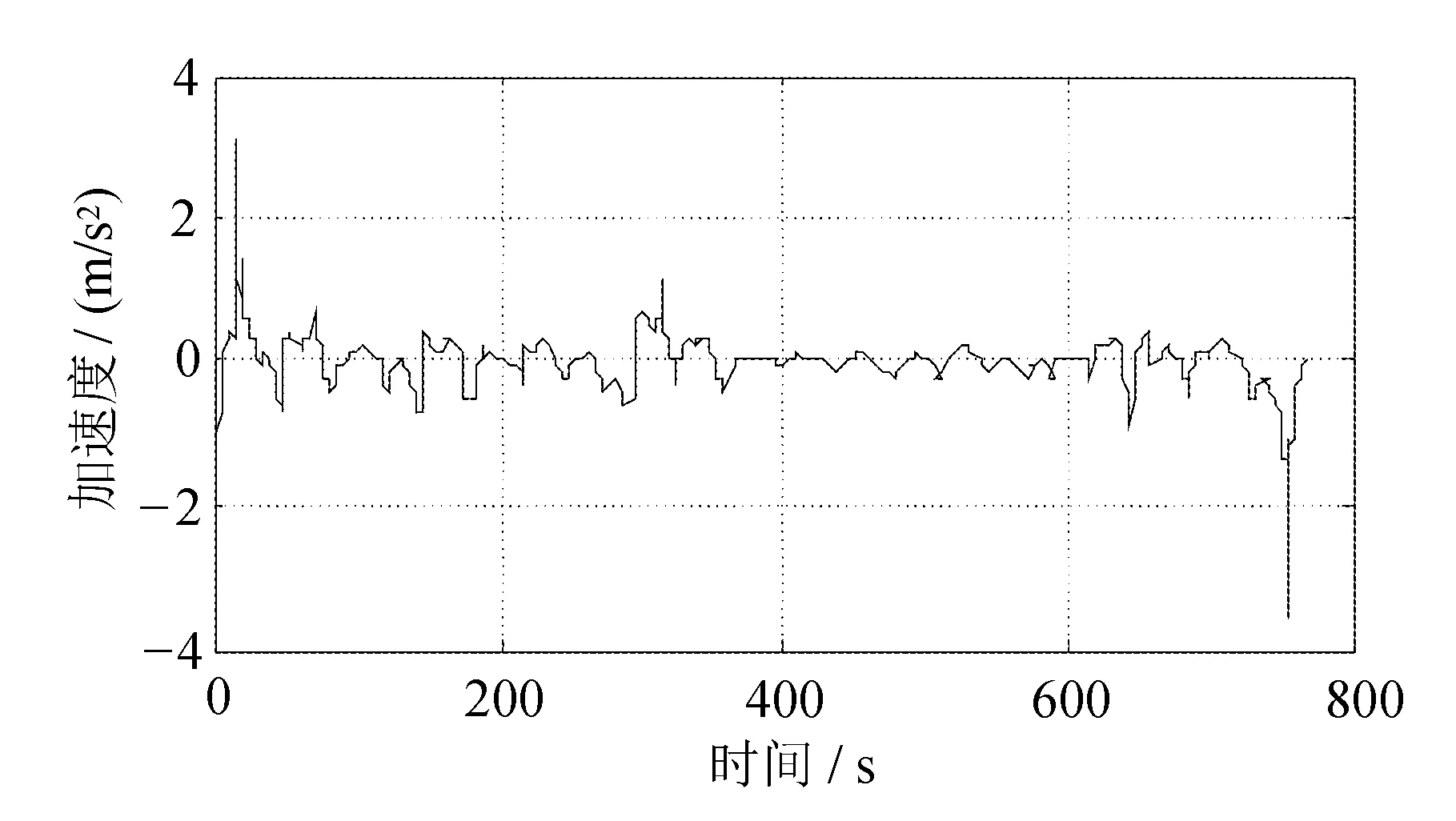
图17 HWFET自车加速度

自车左、右轮的纵向力相同。自车左前轮的纵向力和左后轮的纵向力分别如图18和图19所示。

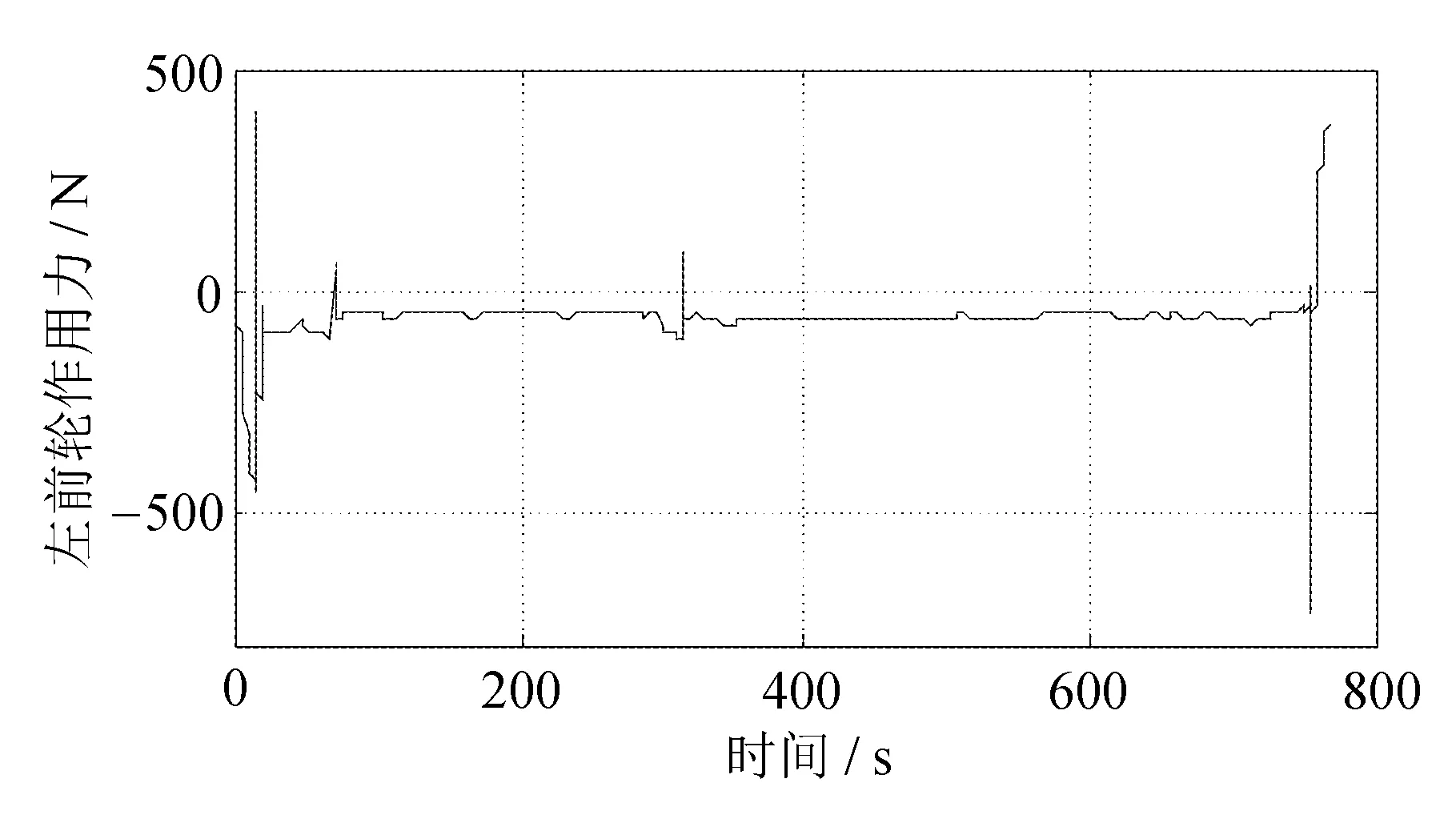
图18 HWFET自车左前轮纵向力

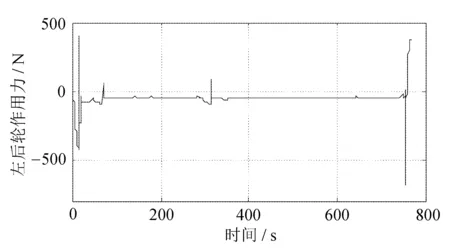
图19 HWFET自车左后轮纵向力

两车的相对距离如图20所示。

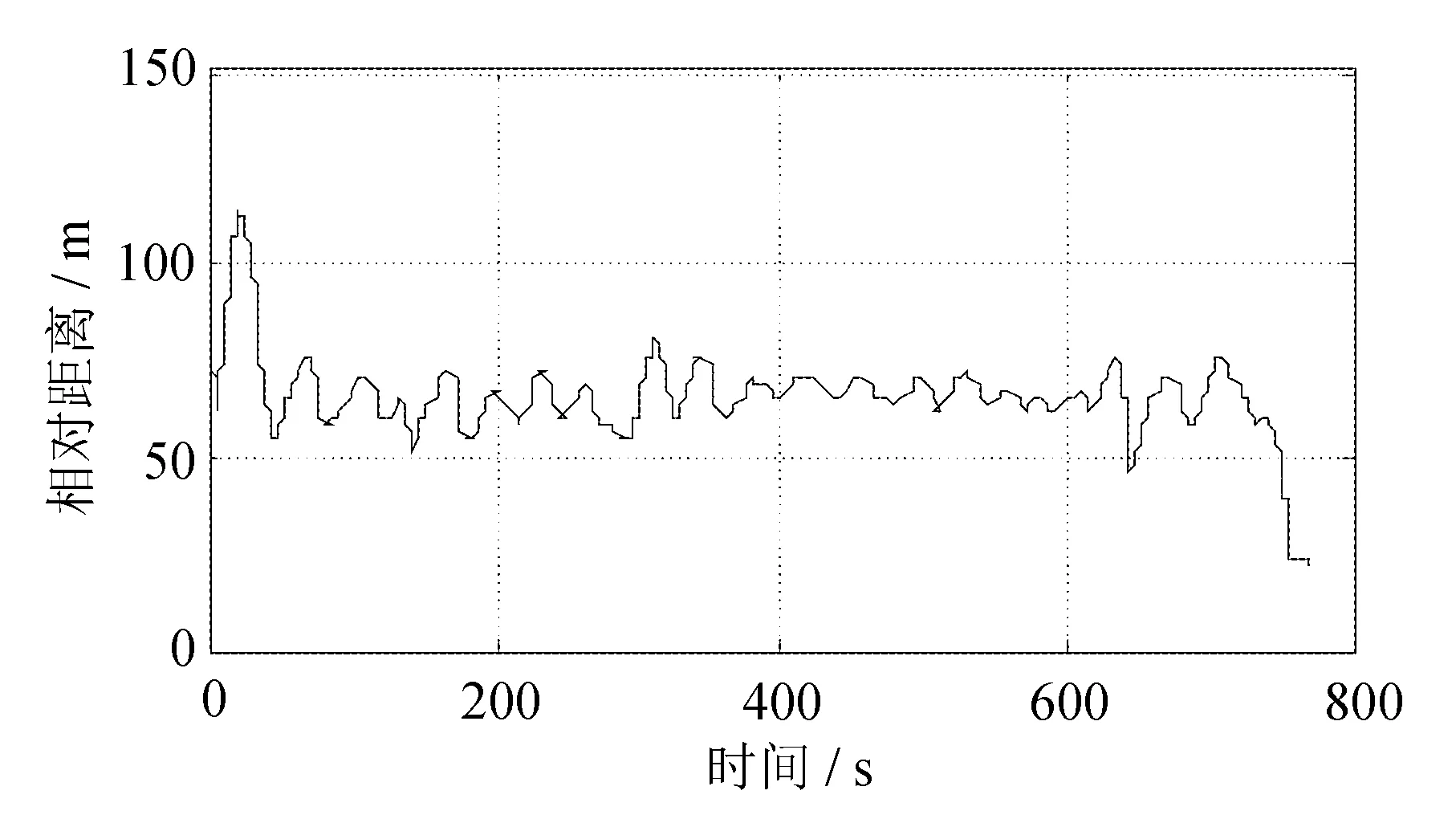
图20 HWFET两车的相对距离

由仿真可得，UDDS和HWFET工况下，两车的相对距离都是正的，且在合理的范围内，可以得出在典型工况中，两车并没有发生碰撞，且跟随距离在合理的范围内，可以证明ACA系统是可实现的、有效的。

6 结 语

提出了基于模糊逻辑控制的ACA系统和简化PMSM模型。根据典型工况下自车ACA系统的仿真与实验结果，得出了如下结论：

1)所设计的基于模糊控制的ACA系统在前车加速和减速行驶条件下，自车都能自动地进行减速或者加速，并且保证最终停车后，自车与前车始终没有发生碰撞，保证了驾驶员和乘坐人员的安全，从而降低驾驶员的劳动强度，并且保证了驾驶者和乘坐人员的安全，电动汽车主动避撞功能基本实现。

2)电动汽车在紧急避撞工况时，必须采用较大强度的制动力矩，但这会带来一些负面因素，例如，会造成驾驶员和乘客暂时的不适，但是这优先考虑到了安全性原则，符合ACA系统将安全性放在第一位的理念，随后自车的减速度在短时间内减小，迅速将其保持在人体可接受的范围，这样的避撞系统更容易被驾驶者和乘坐人员所接受，为电动汽车主动避撞系统的商业化推广提供了便利。

另外，模糊逻辑控制器的设计是ACA系统的核心。在自车跟随前车的过程中，自车加速度变化并不平缓，这会影响车辆的舒适度。所以在未来的研究中，会将提高车辆的操纵稳定性和改善车辆的安全性和舒适性作为研究课题。

参考文献：

[1] World Health Organization. Global status report on road safety 2013: Supporting a Decade of Action [R]. Geneva: WT0,2013.

[2] X F Pei, Z D Liu, G C Ma, et al. Safe distance model and obstacle detection algorithms for a collision warning and collision avoidance system[J]. Automotive Safety and Energy,2012,3(1):26-33.

[3] R Rajamani. Vehicle dynamics and control [J]. New York, USA: Springer,2005.

[4] R H Ge, W W Zhang, W Zhang. Research on the driver reaction time of safety distance model on highway based on fuzzy mathematics[C]//International Conference on Optoelectronics and Image Processing.2010:293-296.

[5] Y F Lian, Y Zhao, L L Hu, et al. Longitudinal collision avoidance control of electric vehicles based on a new safety distance model and constrained regenerative braking strength continuity braking force distribution strategy [J]. IEEE Transactions on Vehicular Technology,2016,65(6):4079-4094.

[6] G Y Li, L J Yang. Neuron-Fuzzy-Prediction control and MATLAB implementation [M]. Beijing: Publishing House of Electronics Industry,2013:223-239.

[7] H Zhang. Study on robust control of permanent magnet synchronous machine drive system[D]. [S.l.]: Dissertation, China University of Mining Technology,2011.

[8] 刘旭，张袅娜，周长哲，等.纯电动汽车横摆力矩滑模控制[J].长春工业大学学报，2017，38(2)：127-132.